
Совсем недавно мы писали о новой головоломке под названием «игра в конфигурации». Она допускает разнообразные модификации и обобщения, предлагаем рассмотреть самые интересные из них.
- Если вы еще не прочли наш лонгрид об игре в конфигурации — скорее переходите по ссылке, а затем возвращайтесь и изучайте более сложные варианты игры.
Теперь вместо крестиков будем использовать цветные квадратики — составленные из них конфигурации воспринимаются легче. Кроме того, их можно быстро и легко рисовать в Word’е, используя цветовую заливку табличных ячеек.
Игра «Не больше трех»
Единственное правило выставления квадратиков здесь следующее: по вертикали, горизонтали и диагоналям не должно стоять более трех соседних (соприкасающихся) квадратиков. Соответственно, допустимы изолированные и объединенные лишь в пары квадратики. В качестве затравки используется пустое поле.
Самая интересная задача состоит в нахождении минимальных и максимальных полных конфигураций для заданных конечных полей, представляющих собой различные геометрические фигуры.
Даже в простейших случаях мы сталкиваемся с нетривиальными задачами комбинаторной геометрии. Рассмотрим, для начала, квадратное поле 4х4, представленное на рисунке 1. Далее листайте галерею право.
 Рисунок 1 Минимальной полной конфигурацией для него будет квадрат, составленный из 3×3=9 квадратиков, примыкающий к любому из четырех углов поля (рис. 2).
Рисунок 1 Минимальной полной конфигурацией для него будет квадрат, составленный из 3×3=9 квадратиков, примыкающий к любому из четырех углов поля (рис. 2). 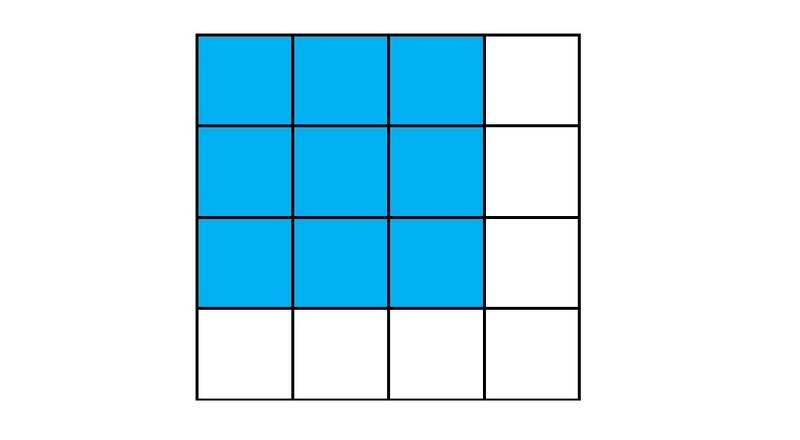 Рисунок 2 Максимальная полная конфигурация представлена на рис. 3. Число квадратиков в ней равно 12.
Рисунок 2 Максимальная полная конфигурация представлена на рис. 3. Число квадратиков в ней равно 12. 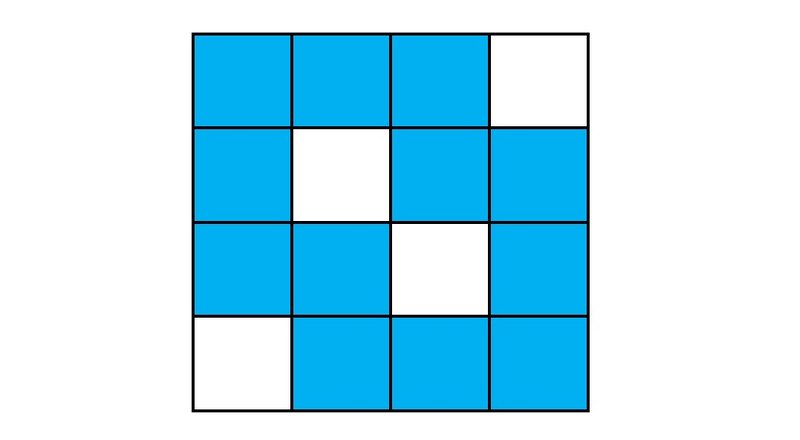 Рисунок 3 Есть ли другие, принципиально отличные от приведенных выше, минимальные и максимальные полные конфигурации? Найдите для этого же поля полную конфигурацию с каким-нибудь промежуточным числом квадратиков, например, 11. Решение представлено на рис. 4.
Рисунок 3 Есть ли другие, принципиально отличные от приведенных выше, минимальные и максимальные полные конфигурации? Найдите для этого же поля полную конфигурацию с каким-нибудь промежуточным числом квадратиков, например, 11. Решение представлено на рис. 4. 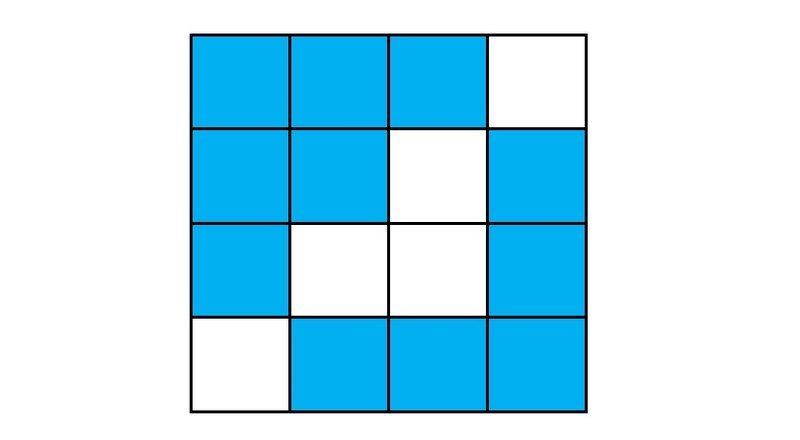 Рисунок 4 Рассмотрим теперь квадратное поле 5×5 (рис. 5). смотреть ещё раз
Рисунок 4 Рассмотрим теперь квадратное поле 5×5 (рис. 5). смотреть ещё раз
- Девушки и автомобили: все розовые автомобили «Моделей года» Playboy 11
- Wilson Combat: самые красивые кастомные «пушки» 26
- Wings For Victory: авиационные британские плакаты 1940-х годов 6
- Рекламные плакаты автомобильных компаний 1910−1930-х 12
- Рекламные фотографии советских тракторов: «Трактороэкспорт» 10
- Рекламные фотографии советских автомобилей: «Автоэкспорт» 12
Рассмотрим теперь квадратное поле 5×5 (рис. 5). Далее листайте галерею право.
 Рисунок 5 Минимальная полная конфигурация для него, представленная на рис. 6, тоже состоит из 9 квадратиков.
Рисунок 5 Минимальная полная конфигурация для него, представленная на рис. 6, тоже состоит из 9 квадратиков. 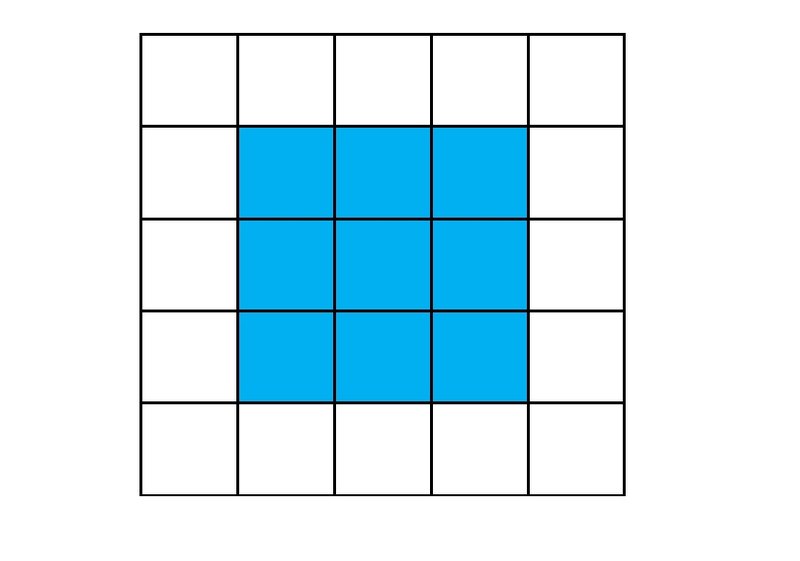 Рисунок 6 Максимальная полная конфигурация состоит из 17 квадратиков (ее варианты представлены на рис. 7 и 8).
Рисунок 6 Максимальная полная конфигурация состоит из 17 квадратиков (ее варианты представлены на рис. 7 и 8).  Рисунок 7
Рисунок 7  Рисунок 8 Найдите другие максимальные полные конфигурации для этого поля. Несложно найти минимальную полную конфигурацию для квадрата 6×6 (рис. 9).
Рисунок 8 Найдите другие максимальные полные конфигурации для этого поля. Несложно найти минимальную полную конфигурацию для квадрата 6×6 (рис. 9).  Рисунок 9 Найдите для него максимальную полную конфигурацию. Найдите минимальную и максимальную полные конфигурации для квадратных полей 7×7, 8×8 и т. д. смотреть ещё раз
Рисунок 9 Найдите для него максимальную полную конфигурацию. Найдите минимальную и максимальную полные конфигурации для квадратных полей 7×7, 8×8 и т. д. смотреть ещё раз
- Девушки и автомобили: все розовые автомобили «Моделей года» Playboy 11
- Wilson Combat: самые красивые кастомные «пушки» 26
- Wings For Victory: авиационные британские плакаты 1940-х годов 6
- Рекламные плакаты автомобильных компаний 1910−1930-х 12
- Рекламные фотографии советских тракторов: «Трактороэкспорт» 10
- Рекламные фотографии советских автомобилей: «Автоэкспорт» 12
Перейдем к полям иных форм. Интереснейший случай — крестообразное поле, изображенное на рис. 10.
 Рисунок 10
Рисунок 10
Найдите для него минимальную полную конфигурацию.
Решив подобную задачу для квадратных полей небольших размеров, можно было бы предположить, что и в данном случае элементами минимальной полной конфигурации будут квадраты, составленные из 3х3=9 квадратиков, или близкие к ним фигуры.
На рис. 11 и 12 представлены соответствующие гипотетические решения.
 Рисунок 11
Рисунок 11  Рисунок 12 смотреть ещё раз
Рисунок 12 смотреть ещё раз
- Девушки и автомобили: все розовые автомобили «Моделей года» Playboy 11
- Wilson Combat: самые красивые кастомные «пушки» 26
- Wings For Victory: авиационные британские плакаты 1940-х годов 6
- Рекламные плакаты автомобильных компаний 1910−1930-х 12
- Рекламные фотографии советских тракторов: «Трактороэкспорт» 10
- Рекламные фотографии советских автомобилей: «Автоэкспорт» 12
Но, оказывается, это не минимальные полные конфигурации, а… наоборот, максимальные. Число квадратиков в них равно 33.
Минимальные же полные конфигурации совершенно иные. Они представлены на рис. 13 и 14. Число квадратиков в них равно 24. Парадоксальным образом, в них встречаются элементы, входящие в максимальные полные конфигурации для квадратных полей.
 Рисунок 13
Рисунок 13 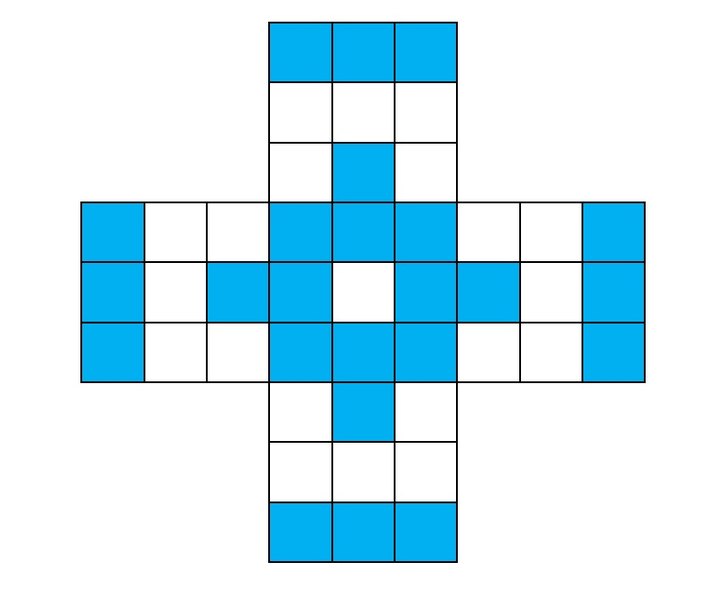 Рисунок 14 смотреть ещё раз
Рисунок 14 смотреть ещё раз
- Девушки и автомобили: все розовые автомобили «Моделей года» Playboy 11
- Wilson Combat: самые красивые кастомные «пушки» 26
- Wings For Victory: авиационные британские плакаты 1940-х годов 6
- Рекламные плакаты автомобильных компаний 1910−1930-х 12
- Рекламные фотографии советских тракторов: «Трактороэкспорт» 10
- Рекламные фотографии советских автомобилей: «Автоэкспорт» 12
Найдите минимальные и максимальные полные конфигурации для ступенчатых диагональных квадратов разных размеров (квадрат 4х4 такого рода представлен на рис. 15).
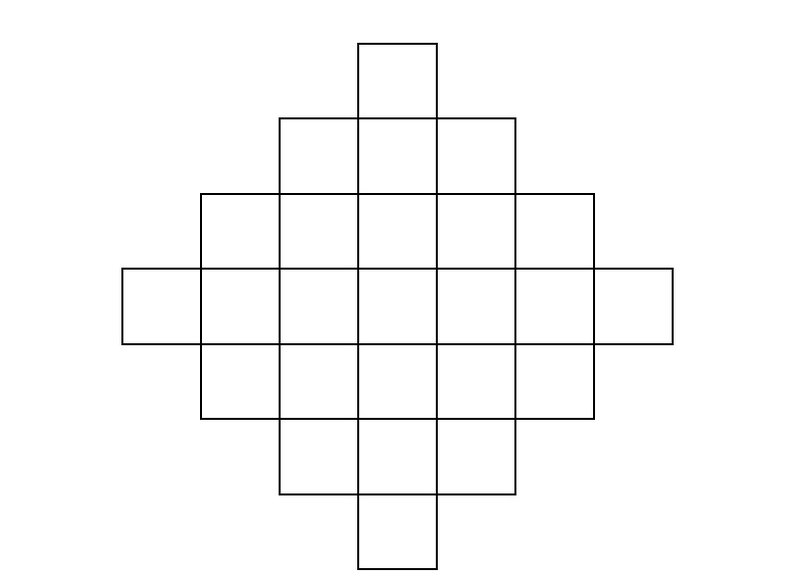 Рисунок 15
Рисунок 15
В игре «Не больше трех» интересны и полные конфигурации на бесконечном поле. Поскольку число квадратиков в них бесконечно, в качестве количественной меры следует использовать плотность, равную пределу (если он существует) отношения n/Sk при k→∞, где Sk = k х k — площадь квадрата со стороной k, а n — число заключенных в нем квадратиков. Плотность не должна зависеть от выбора последовательности увеличивающихся квадратов.
Плотность полной конфигурации, изображенной на рис. 16, очевидно, равна 9/16= 0,5625. Исходя из минимальных полных конфигураций для конечных квадратных полей, можно предположить, что данная полная конфигурация тоже минимальна.
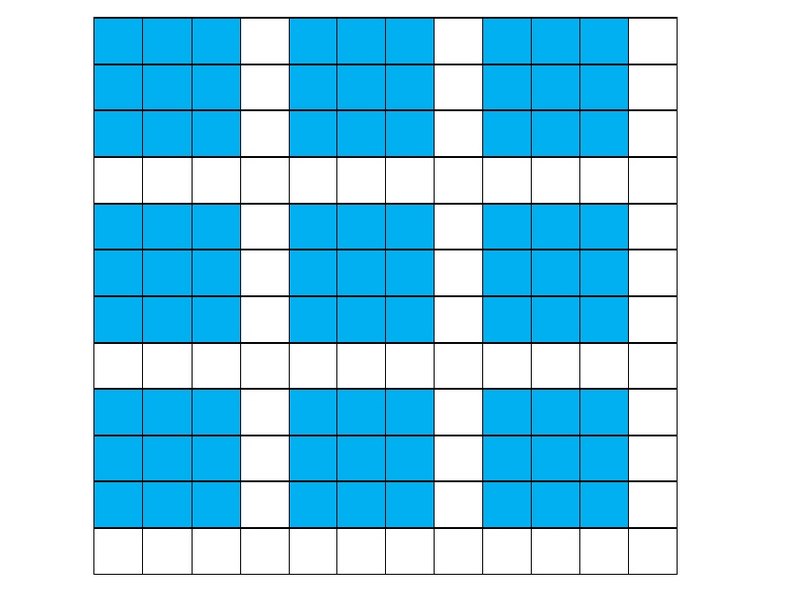 Рисунок 16 Найдите плотность полной конфигурации, представленной на рис. 17.
Рисунок 16 Найдите плотность полной конфигурации, представленной на рис. 17.  Рисунок 17 смотреть ещё раз
Рисунок 17 смотреть ещё раз
- Девушки и автомобили: все розовые автомобили «Моделей года» Playboy 11
- Wilson Combat: самые красивые кастомные «пушки» 26
- Wings For Victory: авиационные британские плакаты 1940-х годов 6
- Рекламные плакаты автомобильных компаний 1910−1930-х 12
- Рекламные фотографии советских тракторов: «Трактороэкспорт» 10
- Рекламные фотографии советских автомобилей: «Автоэкспорт» 12
Максимальная полная конфигурация на бесконечном поле и ее плотность автору пока не известны. Быть может, на этот вопрос сможет ответить наш читатель?






