К вопросу о выпрямителе

Научиться читать несложно. Гораздо труднее научиться сомневаться в прочитанном

Как всегда, причиной написания поста стала реальная ситуация, возникшая в процессе проектирования сетевого адаптера, проводимого моим молодым коллегой (ММК). Возник небольшой спор, в котором участвовал другой ММК и, к своему изумлению, я выяснил, что оказался не вполне прав. Пнп: мои постоянные читатели удивятся, но да, я могу (крайне редко) оказаться на вполне прав и даже могу (еще реже) этот факт признать. Поскольку в данном споре истина таки родилась, решил ею поделиться.

Рассмотрим преобразователь переменного напряжения в постоянное, состоящий из выпрямителя (диодный мост) и накопителя энергии (конденсатор). Схема широко известная (рис 1), принцип работы очевиден, теоретические осциллограммы известны (рис.2), какие вопросы вообще могут возникнуть? Пнп: на самом деле с осциллограммами не все так просто, но об этом позже. Необходимо определить параметры схемы, исходя из свойств первичного (переменного) напряжения и требования к вторичному (постоянному) питанию.

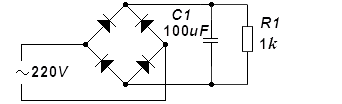
Параметры первичной цепи заданы не нами и принимаются, как данность ~220В, 50Гц, требования к получаемому постоянному напряжению исходят из далее включенного преобразователя - от 120 до 400В, обеспечиваемая мощность 100Вт. Сразу рассчитаем возможные сопротивления нагрузки :
P=U*U/R, откуда R=U*U/P,
тогда диапазон R = {120*120/100 -:- 400*400/100}={144-:-1600} Ом,
и возможные токи I=P/U = {100/120 -:-100/400}={0.834-:-0.25}А, они нам еще пригодятся.
Максимальное значение входного напряжения нам тоже потребуется :Umax=U(действующее)Kf(коэффициент формы)(1+q)(погрешность задания),
для привычной нам сети это 220В*1.41*(1+0.1)=341В.

Мы должны определить требуемые параметры диода и конденсатора. Обратное напряжение на диоде очевидно составляет Umax, или 341В, значение 600В будет приемлемо. Максимально допустимый ток через диод равен максимальному току нагрузки - 834мА, значение 1А приемлемо. Выбираем диодный мост почти любого типа, они все заточены под параметры сети и ток в нашем случае невелик.

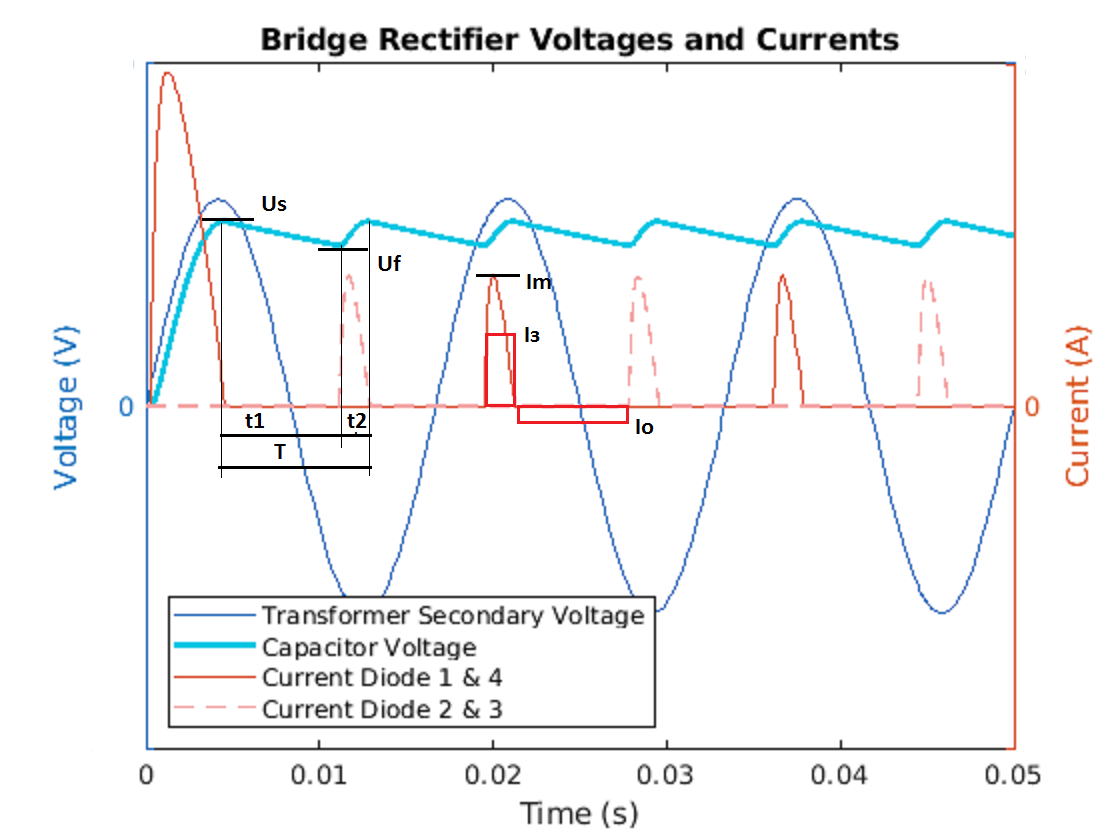
Напряжение на конденсаторе равно Umax = 341В, 450В будут приемлемы. Максимальный допустимый ток через конденсатор равен максимальному току нагрузки - 834мА, значение в 1А приемлемо. А вот емкость сразу не видна, придется считать. Учитываем тот факт, что за время разрядки конденсатора на нагрузку (t2) напряжение может измениться от амплитудного (минимального, это важно) до минимально допустимого. При расчете следует учесть влияние изменения напряжения на ток нагрузки, проще всего считать для нагрузки с постоянной мощностью (а она у нас именно такого типа), тогда из баланса энергии следует
E=P*t1=dEc=Ecs-Ecf=C*Us*Us/2-C*Uf*Uf/2=C/2*(Us*Us-Uf*Uf)
и искомое значение граничной емкости определяем, как
Cmin=2*P*t1/(Us*Us-Uf*Uf). В наихудшем случае (полный разряд емкости) t1=T, где T - половина периода входного сигнала (для 50Гц составит 10мс), Us=220В*1.41*(1-0.1)=280В. Тогда получим Cmin=2*100*10E-3/(280*280-120*120)= 3.1E-5=31мкФ, 47мкФ будет приемлемым значением.
Пнп: внимательный читатель заметит, что мы пренебрегли падением на диодах (порядка 2% от входного напряжения), зависимостью тока от выходного напряжения из-за изменения кпд нагрузки/источника питания (еще 2-3% и еще рядом параметров. Дело в том, что мы делаем грубую прикидку значения емкости, и с неизбежностью будем увеличивать ее на 20% (погрешность емкости) и еще на 20% (погрешность модели), так что точные значения получать нет никакого смысла.
Общее правило выглядит так - если в результате предварительных расчетов Вы получили значение, на 20% отклоняющиеся от предельно допустимых, то у Вас проблемы, нужно иметь минимум полуторо-кратный, а то и кратный запас. Конечно, если Вы проектируете предельные устройства (например, источник питания на 2кВт с кпд 99%), то такой подход Вы себе позволить не можете и считать придется весьма точно, но для нормальных устройств следует придерживаться данной рекомендации.

Можно также получить зависимость амплитуды пульсаций напряжения, как функции емкости, она нам пригодится. Us*Us-(Us-dU)*(Us-dU)=2*P*t/C=Us*Us-(Us*Us-2dU*Us+dU*dU)=2Us*dU-dU*dU и в предположении dU<<U легко получить dU=P*t/(C*Us). Пнп: М25 (да, это шутка такая, вначале я поставил задаче оценку 20, но, после того, как потратил на нее 4 раза по пол-часа, изменил оценку на 25) точное решение квадратного уравнения dU*dU-2dU*U+2*P*t/C=0 получить нетрудно X1,2=(Us+-sqrt(Us*Us-2*P*t/C), однако рассчитать в аналитике простую оценку погрешности приближенного решения мне не удалось, оставляю эту задачу пытливым читателям.
В данном конкретном случае приближенное значение пульсаций равно 53В, точное решение дает нам 60В, разница очевидна, но не столь велика (около 10%).

PS. Автору все-таки удалось сделать оценку точности решения, для чего введем понятие требуемой работы
k=Ep/Ec=P*t/(C*Us*Us/2)=2*P*t/(C*Us*Us)
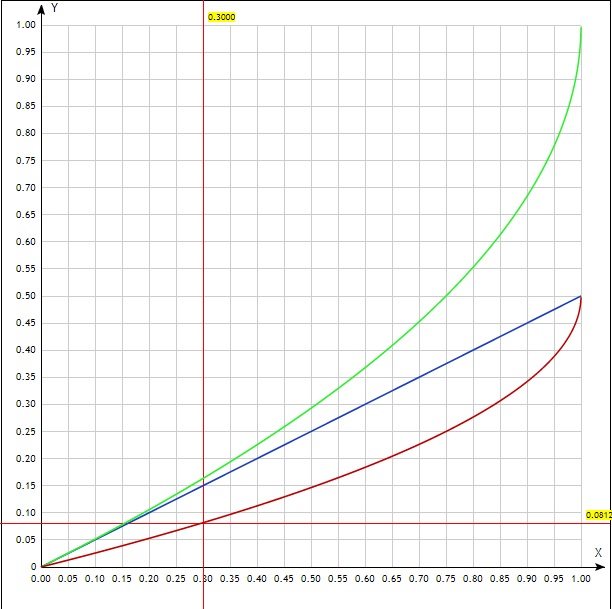
- отношение необходимой для поддержанию нагрузки энергии к имеющейся на начало цикла разряда в емкости энергии. Можно взять и обратный показатель, но он будет меняться от 1 до бесконечности, и работать с ним не слишком удобно, а предложенный показатель меняется от 0 до 1.Пнп: мне представляется совершенно очевидным, что вытащить из конденсатора больше энергии, чем в нем запасено, невозможно, хотя математика с этим не согласна и предлагает сделать амплитуду пульсации комплексным числом, что бы это не означало в реальной жизни. Тогда примерную оценку пульсаций можно записать в виде
qU=dUU=2*P*t/(C*U*U)/2=k/2,
а точное решение принимает вид
1-sqrt(1-k),
причем очевидно, что в области малых k второе выражение стремится к первому. Ну а теперь применим грязный трюк - поскольку мы перешли к безразмерной величине, мы можем построим график обоих функций, найдем разницу между ними и рассчитаем относительное отклонение. Видим, что последнее принимает наибольшее значение на границе диапазона (k=1) и составляет -50%, значит на всем диапазоне изменения k относительная ошибка будет не больше указанной. Для нашего случая k~1/3 ошибка должна быть около 8%, так оно и есть.

Имеет смысл также рассчитать мощность, выделяемую на ESR конденсатора, и, поскольку ток протекает через нее и нагрузку последовательно, то можно принять Pc=P*ESR/Rp, и, если ESR составляет единицы Ом, а сопротивление нагрузки не менее 100 Ом, то мы вправе ожидать на не более 1% от мощности нагрузки, то есть на конденсаторе выделяется не более 1Вт.

Итак, мы получили все требуемые значения и можем выбирать компоненты. Именно так ММК и собирался делать (и я готов был его в этом поддержать), но внезапно другой ММК доказал, что мы неправы и это неверный подход. Дело в том, что параметры по току рассчитаны усредненные, не учтено изменение тока во времени, а производители конденсаторов нормируют именно максимальное значения импульсного тока, а вовсе не среднее (вот она, суть моей ошибки). Не знаю, с чем связаны ограничения на импульс тока, я не произвожу электролитические конденсаторы, но в руководстве по применению от Murata сказано именно так, так что придется рассчитать именно максимальное значение.

Сам по себе расчет не сложен - составляем уравнение вольт-секундного баланса для нашего конденсатора Iз*t2=Io*t1 (на самом деле тут должны стоять интегралы, но мы считаем ток заряда и разряда постоянными) и решаем его, получая Iз=Iо*t1/t2. Введем понятие коэффициента заполнения d=t1/(t1+t2), (можно придумать и другие коэффициенты, но это удобнее всего - он нормирован, то есть принимает значения от 0(t1<<t2) до 1(t2<<t1)) и выразим значение тока зарядки через него
Iз=Io*(t2+t1-t1)/t1=Io*((t2+t1)/t1-t1/t1)=Io*(1/d-1) (1).
Для d=1 получим Iз=0 (и это нормально), для d=1/2 получим Iз=Io (и это правильно, каким током заряжаем, таким же и разряжаем), а вот по мере приближения d к нулю нас ожидает сюрприз - ток зарядки конденсатора начинает резко нарастать и при d=0.1 мы имеем 9-кратное превышение среднего зарядного тока над средним выходным током.

Далее мы можем рассчитать среднее значение тока через конденсатор (оно равно 0, что ожидаемо), а вот среднее абсолютное дает почти двукратное превышение над током нагрузки (что менее ожидаемо, хотя и очевидно). Но нас больше интересует среднеквадратичное значение тока, ведь именно оно определяет мощность, выделяемую на конденсаторе, так что для нахождения эквивалентного по теплу среднего тока придется решить уравнение
Isq*Isq*(t1+t2)=(Iз*Iз*t1+Io*Io*t2)=(Io*t2/t1*Io*t2/t1*t1+Io*Io*t2)=
=Io*Io(t2*t2/t1+t2)=Io*Io*t2/t1*(t2+t1).
Отсюда легко получить Isq=Io*sqrt(t2/t1) или Isq=Io*sqrt(1/d-1) (2).
Опять таки при d=1 получаем Isq=0, при d=1/2 имеем Isq=Io (что верно), но при малых d нас ждет сильное превыщение среднеквадратичного тока через конденсатор над током нагрузки (при d=0.1 получаем Isq=3*Io).

Пнп: заметим, что у нас во всех формулах присутствует выражение 1/d-1 и было бы логично именно его выбрать в качестве характеристики схемы. Подставив значения для d, получим D=1/(t1/(t1+t2))-1=(t1+t2)/t1-1=t2/t1+1-1=t2/t1, назовем его коэффициентом разряда. Да, это значение не нормировано и изменяется от 0(t2<<t1) до бесконечности (t1<<t2), поэтому графики зависимости свойств схемы от данного параметра становятся менее наглядными, зато расчеты становятся проще.

И вот мы приходим к парадоксальному результату: очевидное решение - поставить конденсатор побольше - оказывается не совсем (совсем не) верным. Мы рассчитали необходимое минимальное значение конденсатора, исходя из требований к допустимым пульсациям напряжения, но не следует повышать его без меры. Да, пульсации напряжения будут уменьшаться, но одновременно будет возрастать максимальное значение тока в конденсаторе, а именно оно нормируется (и в диоде, больше току взяться неоткуда, и в источнике, но о нем мы не забоимся, хотя о проводах, может быть, и стоило бы). Также будет возрастать и тепловыделение в этих компонентах, так что идея ограничиться минимально необходимой емкостью конденсатора (конечно, с необходимым запасом) выглядит вполне здраво.

В заключение обсудим самый интересный вопрос - максимальное (не среднее) значение зарядного тока Im. Дело в том, что в предыдущих расчетах мы считали ток постоянным во время фазы заряда емкости, а прямоугольная форма тока в реальных схемах весьма маловероятна. Поэтому мы определили только среднее значение тока зарядки и для определения максимального значения следует учесть коэффициент формы. Для синуса это 1.41, для треугольника - 2, а для обратной экспоненты - лучше не надо о грустном, там все может оказаться еще хуже, скорее всего 2.72. Мы можем определить форму тока четырьмя способами:

1. (правильный) составить систему дифференциальных уравнений (легко) и решить ее в аналитике (а тут сложнее) при заданных граничных условиях;

2. (тоже правильный) применить математический аппарат (операторный метод), перейти в P пространство (легко), решить систему уравнений там в аналитике (легко) и вернуть результат в обычное пространство (если и не сложнее, чем в методе 1, то сравнимо);

3. (в общем-то правильный, но есть нюансы) составить систему дифференциальных уравнений (легко) и решить ее численно (несложно);

4. (сомнительный) сделать правдоподобные предположения (очень трудно) и рассчитать, исходя из них (легко).

Должен признаться, что из институтского курса по электротехнике относительно первых двух способов у меня сохранились только самые общие воспоминания (вообще-то, именно это и является целью высшего образования - запомнить, что искать в справочнике при необходимости), но мы можем совместить способы 3 и 4 - при помощи моделирования выдвинем обоснованные предположения и воспользуемся ими. Собираем схему в любом симуляторе (лично я предпочитаю falstad, но у Вас могут быть свои предпочтения), запускаем моделирование и смотрим на результаты. И видим несомненные треугольники (конечно, это только аппроксимация, истинная форма сигнала будет описываться весьма сложными формулам), поэтому максимальный ток будет равен удвоенному зарядному току, который определяется формулой (1). Убеждаемся в верности модели, при изменении номинала конденсатора наблюдаются изменения амплитуды тока зарядки в хорошем соответствии с полученными ранее формулами. Как и следовало ожидать, максимальное значение тока зарядки конденсатора превышает среднее его значение в 2 раза. Для такой формы сигнала среднеквадратичное значение также несколько увеличивается по сравнению с прямоугольным сигналом, но увеличение на 30% (4/3 от номинала) по сравнению с двукратным максимальным не столь существенно, хотя тоже должно быть принято в внимание.

А вот теперь внимание, вопрос на засыпку - почему у меня в симуляторе получились треугольные сигналы, а в книге "Практическая схемотехника" на рисунке 6.23 (и во многих других печатных и электронных материалах) показаны импульсы тока в виде верхушек синусоиды. Пнп: очень дельная книга, настоятельно рекомендую для начального и среднего уровней и дело совсем не в том, что написана она моим Шефом -генеральным директором нашего предприятия, д.т.н., лауреатом и так далее, а в том, что книга очень даже неплохая. Будь она плохая ... ну вряд ли бы написал об этом честно, скорее просто не упомянул бы и уж точно не хвалил бы. Так вот, возвращаясь к теме повествования, и мне удалось в симуляторе получить близкую к обрезанной синусоиде форму зарядного тока конденсатора и ключевое слово тут ... ESR - в применяемой мною системе моделирования конденсаторы идеальны, если явно не указано иное. Если имитировать данный параметр с помощью явно включенного последовательного резистора и поиграть с его номиналом, по можно увидеть трансформацию почти прямоугольного треугольника в нечто загадочное (см рис. 2) а затем и в очень напоминающую отрезок синусоиды кривую. И хотя, скорее всего, это не фига не синусоида, для инженерных расчетов мы можем считать ее таковой. Аналогичный результат получается, если поставить сопротивление, имитирующее сопротивление тела диода, что вполне ожидаемо, ведь включены они последовательно в цепи заряда.

Важное замечание - да, учет паразитных параметров изменил форму кривой и снизил максимальный ток с 2*Iз до 1.41*Iз, но площадь под кривой осталась прежней, так что формула (1) по прежнему верна и по прежнему следует учитывать кратное превышение зарядного тока конденсатора (и тока диода) над током нагрузки. Оценим масштаб проблемы - для принятых нами допустимых условий пульсация выходного напряжения от 248(220*0.8*1.41)В до 120В время разряда соответствует времени изменения синусоиды от максимального значения до 120/248=0.5 амплитуды, arccos(0.5)=60, тогда d=60/(60+120)=1/3, что означает (при токе нагрузки 500мА) зарядный ток конденсатора 1А и ток диода 1.5А с импульсом 1.41 и 2.1А соответственно. Но, если мы увеличим конденсатор до 480 мкФ, то амплитуда пульсаций на конденсаторе упадет приблизительно в четыре раз, arccos(7/8)=30, следовательно d=30/180=1/6 и мы видим зарядный ток конденсатора 2.5А и ток диода 3А с импульсом в 3.5 и 4.2А соответственно, а если конденсатор и диод очень хорошие (с малым сопротивлением), то и 5 и 6А, что заставит более внимательно отнестись к выбору соответствующих компонентов, учитывая указанные превышения действующих и максимальных значений.

В заключение позволю выразить надежду, что у моих читателей после прочтения настоящего поста никогда не возникнет проблем с данным аспектом проектирования электроники.