Для некоторых датчиков ускорения требуется дополнительная калибровка нуля после монтажа на плату. Когда я увидел несколько исходников с калибровкой датчиков ускорения, где составляющая G учитывалась просто путём вычитания из оси Z величины = 9,8 м/с2 — появилась идея написать данную заметку.
Структура публикации
- Проблема
- Постановка задачи и способ решения
- Как правильно получить точки?
- Как вычислить центр шара?
- Как ускорить поиск центра шара?
- Как ещё ускорить поиск центра шара?
- Об ошибках при замерах
- Итог
Проблема
В чём проблема — МЕМС-датчики после монтажа в плату претерпевают незначительные деформации, которые влияют на:
- положение нуля;
- масштабирование измеряемых величин;
- перпендикулярность осей к друг-другу.
И если масштабирование и перпендикулярность нарушаются не так заметно, то положение нуля сбивается ощутимо. Например, если перевести типичную величину смещения нуля для акселерометра датчика MPU9250 в м/с2, то это получается в районе 0,2 м/с2. Т. е. датчик неподвижен, но при этом показывает ускорение, а через 5 секунд мы получаем скорость в 1 м/с. С одной стороны, все данные датчиков всегда пропускают через какой-либо фильтр (например такой). Но с другой стороны зачем фильтру постоянно компенсировать это смещение? Ведь датчик будет показывать движение там, где его нет. Это снижает точность результата. А всего то нужно один раз найти величину смещения и потом во время работы датчика вычитать эту величину из его показаний.
Простейшее решение для поиска величины смещения нуля, которое сразу приходит в голову — это создать условия, при которых датчик точно должен показывать ноль. Значение, регистрируемое на датчике — это и есть величина смещения нуля! Так? Но нет — на акселерометр постоянно действует сила тяжести. Чтобы её избежать, понадобится невесомость (подбрасывание не подойдёт). На компас действует магнитное поле Земли, а на гироскоп её вращение. Так что, если у вас нет персонального звездолёта, то придётся что-то придумать.
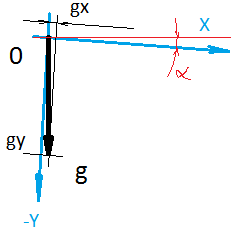
Второе решение, которое сразу приходит в голову — это поставить датчик (а точнее его оси) в такое положение, при котором мы точно будем знать, что должен показывать датчик. Разница между тем, что датчик показывает и тем, что он должен показывать — и будет смещение нуля! Так? Например, мы знаем, что если акселерометр поставить в уровень с горизонтом, то по идее, вектор ускорения свободного падения будет направлен точно вдоль оси Z датчика. Величину вектора ускорения мы знаем.
Однако есть проблема. Заключается она в том, что мы не можем точно установить оси датчика в уровень с горизонтом. Дело в том, что поверхность на которую мы будем опираться не параллельна печатной плате. Та в свою очередь не параллельна площадке на которой расположен датчик. Сам датчик не ровно стоит на своей площадке и оси внутри датчика не параллельны корпусу датчика. Погрешность в установки оси относительно горизонта на 1 градус, даёт проекцию, сопоставимую по размерам с величиной самого смещения нуля, которое мы хотим найти. В случае магнитометра, мы вдобавок не знаем, куда направлен вектор магнитного поля. В теории — на север. Но на практике, само магнитное поле Земли неоднородно по напряжённости и направлению. Плюс ближайшие металлические предметы вносят свои коррективы.
Постановка задачи и способ решения
Задача звучит так: нужно определить вектор смещения нуля, используя показания датчика, который всегда будет регистрировать вектор смещения + постоянный вектор внешнего воздействия (ускорение свободного падения, вращение Земли, магнитное поле Земли), величину и направление которого мы не знаем (в случае с акселерометром величину мы знаем, но опять же масштаб датчика может быть не равен 1).
Способ решения. В данной статье предлагается определять вектор смещения следующим образом. Мы берём и крутим датчик по всякому и регистрируем показания датчика. После N измерений, величины взятые с датчика и расположенные на графике будут представлять собой шар, радиус которого — это величина внешнего воздействия, а центр — это как раз искомая величина смещения нуля.
Как правильно получить точки?
Для облегчения самой процедуры измерения, можно написать простенькую программу. Она должна фиксировать показание датчиков, когда прибор неподвижен. Нам останется только поворачивать прибор в нужные положения. Для того, чтобы определить неподвижное состояние, подходит и не калиброванный акселерометр — просто берём разницу между текущим значением и предыдущим. И если больше уровня шума, то значит фиксируем движение. У меня порог получается в районе 0,07G. Если держите руками, будет получаться больше этого значения. Я использовал для фиксации положения малярный скотч. Если всё-равно не получается — проверьте, нет ли рядом холодильника, вентилятора или чего-то подобного.
// здесь у вас глобальные по модулю переменные
static TSumSensorsData g_sens_data[2];
static int32_t g_sens_data_sum_cnt[2];
static uint8_t g_sens_data_num;
// здесь какое-то прерывание, при получении данных с датчиков
IS_INTERRUPT void on_dma_raw_ready_calibrate_step1()
{
SensorRawBuffer *raw = sensor_get_raw_buffer();
g_sens_data[g_sens_data_num].acc_x += swap_i16(raw->accell_x_unswap);
g_sens_data[g_sens_data_num].acc_y += swap_i16(raw->accell_y_unswap);
g_sens_data[g_sens_data_num].acc_z += swap_i16(raw->accell_z_unswap);
g_sens_data[g_sens_data_num].gyro_x += swap_i16(raw->gyro_x_unswap);
g_sens_data[g_sens_data_num].gyro_y += swap_i16(raw->gyro_y_unswap);
g_sens_data[g_sens_data_num].gyro_z += swap_i16(raw->gyro_z_unswap);
g_sens_data[g_sens_data_num].mag_x += raw->mag_x_raw * g_mag_calibrate.kx;
g_sens_data[g_sens_data_num].mag_y += raw->mag_y_raw * g_mag_calibrate.ky;
g_sens_data[g_sens_data_num].mag_z += raw->mag_z_raw * g_mag_calibrate.kz;
g_sens_data_sum_cnt[g_sens_data_num]++;
}
//это вызывается из main
void sensors_calibrate_program(FlashROM *flash_ptr)
{
double calibrate_result_error[3];
TVector16 calibrate_result[3];
int32_t radius[ACCEL_NO_MOTION_DETECT_COUNT];
uint8_t raw_is_deleted[ACCEL_NO_MOTION_DETECT_COUNT];
TVector16 raw[3][ACCEL_NO_MOTION_DETECT_COUNT];
. . .
// определяю неподвижность
g_sens_data_sum_cnt[0] = 0;
g_sens_data_num = 0;
int16_t prev_avg_x = 0;
int16_t prev_avg_y = 0;
int16_t prev_avg_z = 0;
int8_t low_motion_cnt = 0;
while(low_motion_cnt < ACCEL_NO_MOTION_DETECT_COUNT)
{
if (g_sens_data_sum_cnt[g_sens_data_num] >= ACCEL_NO_MOTION_DETECT_SAMPLES)
{
uint8_t new_data_num = (g_sens_data_num + 1) & 1;
g_sens_data[new_data_num].acc_x = 0;
g_sens_data[new_data_num].acc_y = 0;
g_sens_data[new_data_num].acc_z = 0;
g_sens_data[new_data_num].gyro_x = 0;
g_sens_data[new_data_num].gyro_y = 0;
g_sens_data[new_data_num].gyro_z = 0;
g_sens_data[new_data_num].mag_x = 0;
g_sens_data[new_data_num].mag_y = 0;
g_sens_data[new_data_num].mag_z = 0;
g_sens_data_sum_cnt[new_data_num] = 0;
uint8_t old_data_num = g_sens_data_num;
g_sens_data_num = new_data_num; // вот эта операция не может быть выполнена во время работы прерывания
// (так по-простому можно разделить два потока, не имея операционки)
// здесь всё очень просто - нахожу среднюю
int16_t avg_x = g_sens_data[old_data_num].acc_x / g_sens_data_sum_cnt[old_data_num];
int16_t avg_y = g_sens_data[old_data_num].acc_y / g_sens_data_sum_cnt[old_data_num];
int16_t avg_z = g_sens_data[old_data_num].acc_z / g_sens_data_sum_cnt[old_data_num];
// собственно получаю разницу с предыдущим значением
int16_t dx = avg_x - prev_avg_x;
int16_t dy = avg_y - prev_avg_y;
int16_t dz = avg_z - prev_avg_z;
prev_avg_x = avg_x;
prev_avg_y = avg_y;
prev_avg_z = avg_z;
// если акселерометр регистрировал низкую активность
if ((abs_i16(dx) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dy) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dz) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE))
{
// тогда мы регистрируем точку
raw[RAW_ACC][low_motion_cnt].x = avg_x;
raw[RAW_ACC][low_motion_cnt].y = avg_y;
raw[RAW_ACC][low_motion_cnt].z = avg_z;
raw[RAW_GYRO][low_motion_cnt].x = g_sens_data[old_data_num].gyro_x / g_sens_data_sum_cnt[old_data_num];
raw[RAW_GYRO][low_motion_cnt].y = g_sens_data[old_data_num].gyro_y / g_sens_data_sum_cnt[old_data_num];
raw[RAW_GYRO][low_motion_cnt].z = g_sens_data[old_data_num].gyro_z / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].x = g_sens_data[old_data_num].mag_x / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].y = g_sens_data[old_data_num].mag_y / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].z = g_sens_data[old_data_num].mag_z / g_sens_data_sum_cnt[old_data_num];
low_motion_cnt++;
// даём звуковой сигнал
beep();
// и даём фору себе 2 секунды отклеить скотч, пока датчик в руках - программа регистрирует движение
// прилепили - получили точку
// поэтому всё получится быстро и весело
delay_ms(2000);
}
}
}
. . .
}
Чтобы получить шар на графике, нужно крутить устройство с датчиком по определённой схеме. Для этих целей хорошо подойдёт глобус, так как имеет разметку. Можно подумать, что лепить нужно по всему глобусу. Но это не так.
Нужно датчик лепить не по всей поверхности глобуса, а на один меридиан. Допустим берём семь точек на меридиане (первая и последняя на северном и южном полюсе). В каждой точке меридиана прикладываем ваше устройство к глобусу и ещё крутим устройство вокруг своей оси с определённым шагом, например 30-35 градусов. Получается если вокруг своей оси поворачивать 12 раз, то в 7 точках всего получается 84 замера.

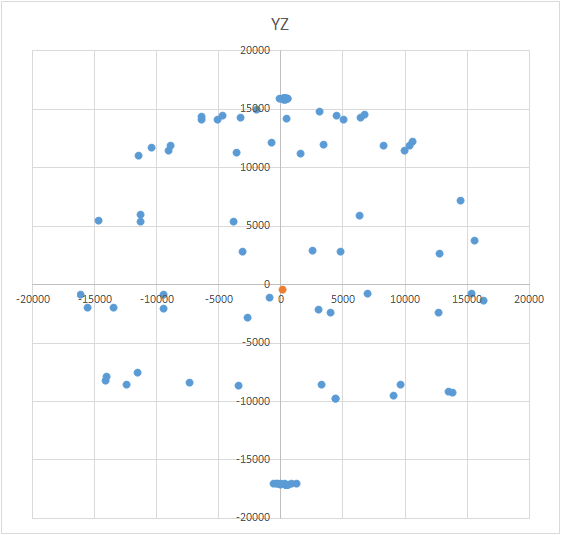
Прелесть метода в том, что всё можно сделать “на коленке”. Точность позиционирования особой роли не играет, просто нужно крутить по схеме, чтобы вектор внешнего воздействия на графике нарисовал шар. Правильный выглядит примерно так — см. рис (отметкой обозначен центр).
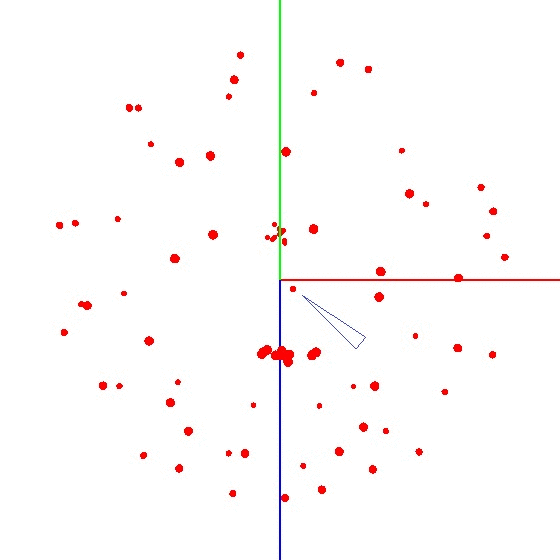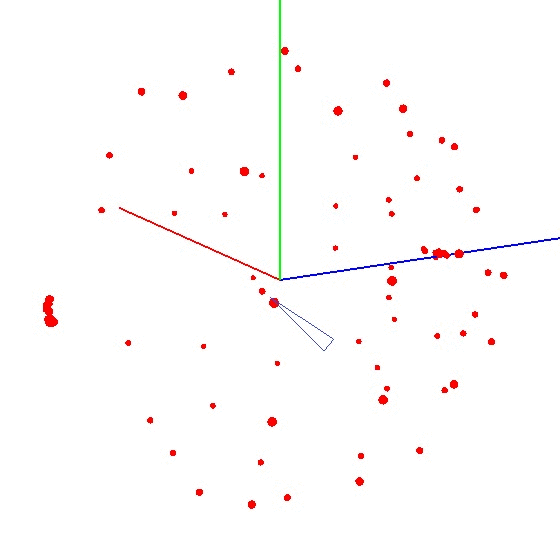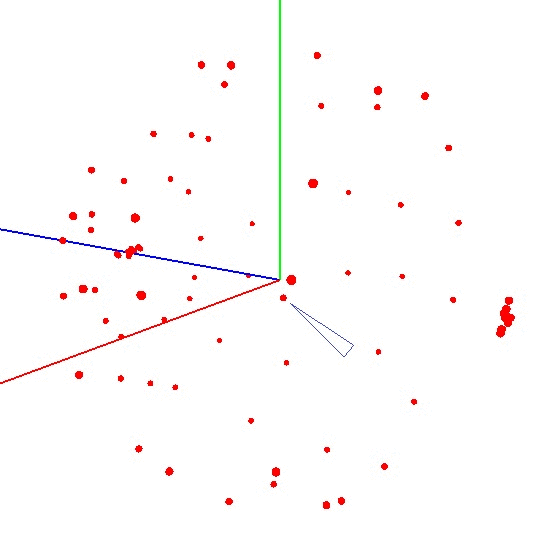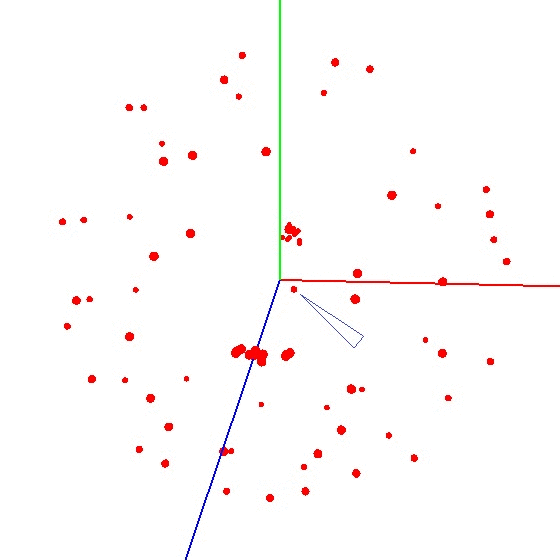
Как вычислить центр шара?
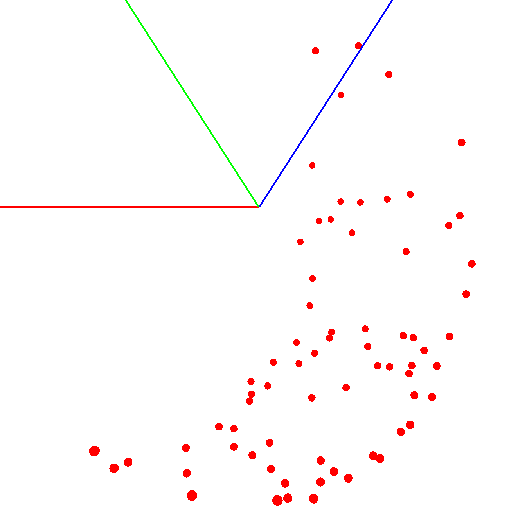
Это интересная задача и у неё несколько вариантов решения. Может показаться, что для поиска центра достаточно взять среднее арифметическое по координатам полученных точек. Однако это не так — точки могут быть расположены на шаре неравномерно (см. рис).
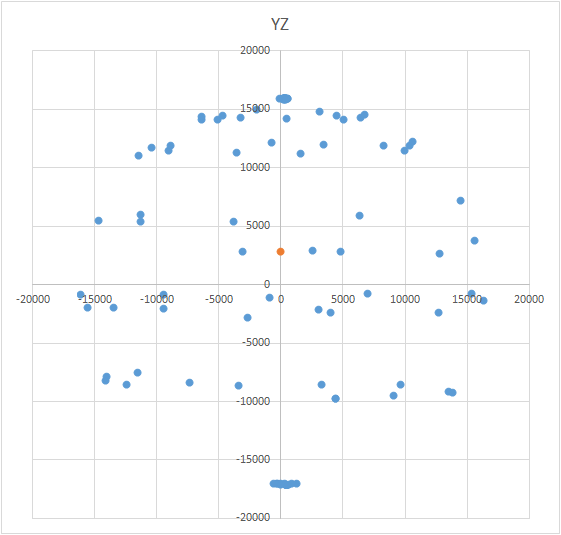
Уравнение шара выглядит так: (X — A)2 + (Y — B)2 + (Z — C)2 = R2, где X, Y, Z — координаты точки, лежащей на шаре. A, B, C — это координаты центра на осях x, y и z соответственно. R — радиус шара. Можно построить систему уравнений и каким-то методом постараться попроще решить эту систему. А можно просто перебором найти центр (это типа метод последовательных приближений). Смысл метода прост: величина ошибки (X — A)2 + (Y — B)2 + (Z — C)2 — R2 должна стремиться к нулю. А значит сумма этих величин для всех точек сферы также должна стремиться к нулю. Зная это, мы можем подобрать такие значения A, B и C, для которых величина ошибки для всех точек будет минимальной. Зона перебора ограничивается габаритами шара (условный куб). То есть мы последовательно должны поставить центр шара во все точки куба и посчитать ошибку. Там где минимальная ошибка — там и центр.
В качестве R нужно брать теоретическую величину вектора внешнего воздействия — для акселерометра, это ускорение свободного падения, для компаса — это средняя величина магнитного поля Земли, для гироскопа — скорость вращения Земли. Разумеется в формуле должны быть величины одной размерности (условные единицы датчика или м/с2, градус/с и т. д.). Удобней пересчитывать в условные единицы соответствующего датчика.
Например: Сколько условных единиц должен показать 16-битный датчик ускорения с пределом измерения ±2g при воздействии на датчик только ускорения свободного падения?:
9,8 м/с2 * 65536 / (2g + 2g) = 9,8 м/с2 * 65536 / (2 * 9,8 м/с2 + 2 * 9,8 м/с2) = 16384 у. е. датчика.
Кстати, если точно знать радиус шара, то можно вычислить центр только по его «дольке». То есть по точкам, которые расположены только на кусочке поверхности шара. Но это не наш случай.
Как ускорить поиск центра шара?
Нужно искать центр не во всём кубе (габариты шара), а по линии, начало у которой произвольное, каждая следующая точка ближе к действительному центру и окончание — в центре. Предположим, что мы начинаем с точки (0; 0; 0)… Мы всегда движемся с постоянным шагом. Поэтому если представить набор кубиков 3х3х3, где каждая грань равна величине шага и также представить, что текущее положение — это средний кубик, то у нас есть 9 + 8 + 9 вариантов, куда поставить следующую точку. Мы просто должны находясь в каждой точке, посчитать в какой из соседних 26 точках ошибка будет меньше. Если окажется, что ошибка меньше в текущей точке, а не в одной из соседних, то значит она стоит в центре и перебор окончен.
Public Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
Do While True
min_sigma = 0
For ai = -1 To 1
For bi = -1 To 1
For ci = -1 To 1
sigma = get_err(A + ai, B + bi, C + ci, 16384)
If sigma < min_sigma Or min_sigma = 0 Then
ai_min = ai
bi_min = bi
ci_min = ci
min_sigma = sigma
End If
Next
Next
Next
If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
Exit Do
End If
A = A + ai_min
B = B + bi_min
C = C + ci_min
Loop
. . .
Как ещё ускорить поиск центра шара?
Нужно искать с переменным шагом. Сначала ищем центр крупным шагом. Нашли центр, уменьшаем шаг и от него начинаем искать дальше. И так далее, пока не получите результат необходимой точности.
Public Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
step = 1000
Do While True
min_sigma = 0
For ai = -1 To 1
For bi = -1 To 1
For ci = -1 To 1
sigma = get_err(A + ai * step, B + bi * step, C + ci * step, 16384)
If sigma < min_sigma Or min_sigma = 0 Then
ai_min = ai
bi_min = bi
ci_min = ci
min_sigma = sigma
End If
Next
Next
Next
If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
step = step / 10
If step < 0.01 Then
Exit Do
End If
Else
A = A + ai_min * step
B = B + bi_min * step
C = C + ci_min * step
End If
Loop
. . .
Об ошибках при замерах
Во время замеров могут быть ситуации, когда по каким-то причинам результат замера может оказаться сильно дальше от поверхности шара. Или это может быть множество точек. Или вообще в результате замеров может получиться не шар, а “яйцо” или “дирижабль”. В этом случае, разумеется, нужно повторить все замеры, выявив возможные причины ошибок. Например, для магнитометра это может быть болт или гвоздь в столе и прямо над ним вы проводите замеры. И чем ниже по мередиану опускать датчик, тем сильнее металл будет влиять на результат. Поэтому нужно определить порог допустимой величины ошибки. Чтобы не переделывать замеры из-за нескольких явно ошибочных точек, можно применить фильтр. Принцип действия фильтра очень простой — вычислив первый раз центр, отсортируйте точки по уровню ошибки в каждой из них. Часть точек с наибольшей ошибкой можно просто выбросить (например 10%). Затем нужно повторить поиск центра.
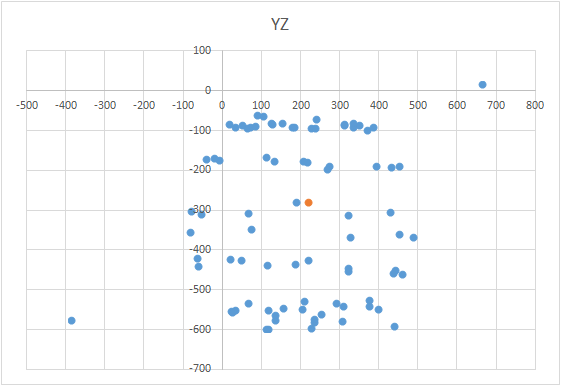
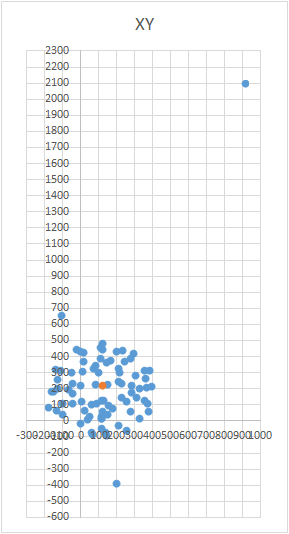
Итог
У метода довольно хорошая точность. Метод позволяет обходиться простыми подручными средствами (мяч, банка и т. п.). Достаточно быстро работает. Простой код. Во многих датчиках есть специальные регистры, куда можно записать найденное значение, и датчик будет сам на лету его вычитать. Такие регистры обычно имеют префикс «TRIM», как в MPU9260, или «OFFSET», как в LSM303. А вот всем известный LIS302DL таких регистров не имеет.
Не забывайте ставить плюсик, если понравилось. Пишите в комментариях свои способы калибровки датчиков.
Автор: 1div0






