Вся окружающая нас электроника состоит из отдельных микросхем, более сложная электроника – из построенных на их основе функциональных блоков.
На данном этапе компьютеры буквально создают сами себя, стало невозможно синтезировать даже самый простой микропроцессор без применения вычислительного устройства.
Но что же все-таки лежит в основе самой микросхемы? Как создать простейшее цифровое устройство с требуемой выходной функцией?
Под катом — пример синтеза устройства со всей необходимой теорией.
Немного теории
Все элементарные цифровые устройства (ЦУ) делятся на комбинационные и последовательностные. В комбинационных ЦУ выходные сигналы однозначно определяются комбинацией входных сигналов, действующих в данный момент. Выходные сигналы (функции) последовательностных ЦУ определяются последовательностью изменения входных сигналов (координат).
В основе практически всех цифровых микросхем лежат простейшие логические элементы И, ИЛИ, НЕ. Естественно, что вариантов реализации ЦУ может быть очень много, в зависимости от комбинаций составных элементарных логических элементов. Поэтому оговоримся заранее, что синтез будем производить в базисе И-НЕ, т.е. используем в ходе построения ЦУ только этот элемент.
Думаю, что аудитория Хабра знает основы алгебры логики. Приведу только парочку формул:
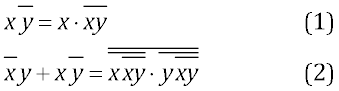
Постановка задачи
В данной статье рассмотрим пример синтеза последовательностного ЦУ. В качестве примера возьмем преобразователь из прямого кода в дополнительный (для трехразрядного кода).
Дополнительный код числа образуется путем прибавления 1 к младшему разряду инвертированного числа. Например, имеем число А = 10110 (старший разряд слева). Тогда обратный код для А — 01001, а дополнительный — 01010.
Синтез устройства
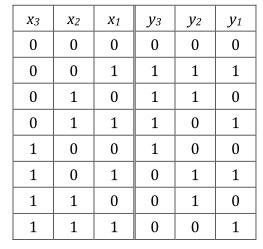
Для начала составим таблицу истинности.
Обозначения: х — входные сигналы, у — выходные. Индекс «1» — у младшего бита.
Теперь необходимо выразить выходные сигналы в зависимости от входных с помощью простейших логических функций (по условию задания, будем пользоваться базисом И-НЕ).
Чаще всего используют две формы записи — совершенную дизъюнктивную нормальной форму (СДНФ) и совершенную конъюнктивную нормальную форму (СКНФ).
В первом случае, каждому набору переменных из таблицы истинности ставится в соответствие минтерм — логическое произведение всех переменных, которые входят в прямом виде, если значение переменной равно 1, или в инверсном виде, если значение переменной равно 0. Любую логическую функцию можно представить в виде логической суммы минтермов, соответствующих единичным наборам переменных (наборам, при которых логическая функция принимает значение 1). Такое представление и называется СДНФ. Для реализации ЦУ в базисе И-НЕ целесообразно представлять выходную функцию именно в виде СДНФ.
В случае СКНФ все прямо противоположно. Функция представляется в виде логического произведения макстермов. Макстерм — логическая сумма всех переменных, которые входят в прямом виде, если значение переменной равно 0, или в инверсном виде, если значение переменной равно 1.
Запишем выходную функцию y1 в виде СДНФ:
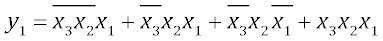
Карты Карно
Видно, что выражение получилось достаточно длинным. Его можно упростить, применяя правила поглощения и склеивания. Для того, чтобы не делать лишних действий, можно сразу получить минимизированную функцию. Для этого можно применить метод карт Карно.
Карта представляет собой таблицу, каждая клетка которой соответствует одному из наборов таблицы истинности. Для логической функции трех переменных карта Карно представляет собой два горизонтальных ряда по четыре клетки. Смысл применения карт Карно определяется специально выбранным порядком нумерации клеток, при котором любой соседней паре клеток с единицами или нулями по горизонтали или вертикали соответствуют склеивающиеся слагаемые или сомножители формулы. Если структурная формула получается на основе СДНФ, то учитываются только клетки карты, определяющие единичные наборы. (В случае СКНФ — нулевые).
Соседние клетки карты с единицами или нулями объединяются в группу. При объединении пользуются следующими правилами:
1) соседними являются не только клетки, расположенные рядом по горизонтали и вертикали, но и клетки на противоположных краницах карты;
2) клетки могут объединяться по 2, по 4, по 8 и т.д.;
3) одна и та же клетка может входить в несколько групп;
4) минимизированная структурная формула записывается на основе наименьшей совокупности групп, которая захватывает (покрывает) все либо единичные (если используется СДНФ), либо нулевые (СКНФ) клетки.
В первом случае структурная формула предстваляет собой логическую сумму, каждое из слагаемых которой соответствует одной из групп карты. При этом в каждое слагаемое входят лишь те переменные, которые не меняют своего значения в наборах, соответствующих объединенным клеткам. Во втором случае в группы объединяют нулевые клетки, минимизированная структурная формула представляет собой логическое произведение, каждый сомножитель которого записывается на основе группы карты.
Далее будем указывать в наших картах только единичные наборы. «Нулевые» клетки будем оставлять пустыми.
Пора уже начинать...
Итак, приступим к синтезу нашего устройства, руководствуясь вышеизложенной теорией.
Для начала составим карты Карно для всех выходных функций (их у нас три, как и входных). Кружочком помечены клетки, объединяемые в одну группу. Обратите внимание, суммируем произведения неизменяющихся (в данной группе )входных сигналов с соответствующим логическим уровнем. Количесвто слагаемых равно количеству групп-объединений. В первой карте объединены 2-я и 3-я клетки, а также 3-я и 4-я. Во второй — 2-я и 6-я, а также 4-я и 8-я. В третьей карте в одну группу объединены 2, 3, 6, 7-я клетки.
Далее справа записываем в соответствии с правилами объединения клеток минимизированные выходные функции. Т.к. нам нужно получить их в определенном базисе, применяем алгебру логики, а именно формулы (1) и (2) и выражаем функции через входные переменные.
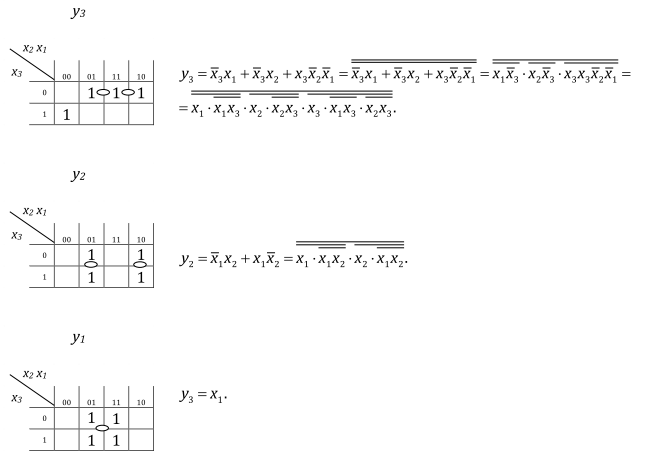
Теперь можем синтезировать наше ЦУ по полученным функциям:
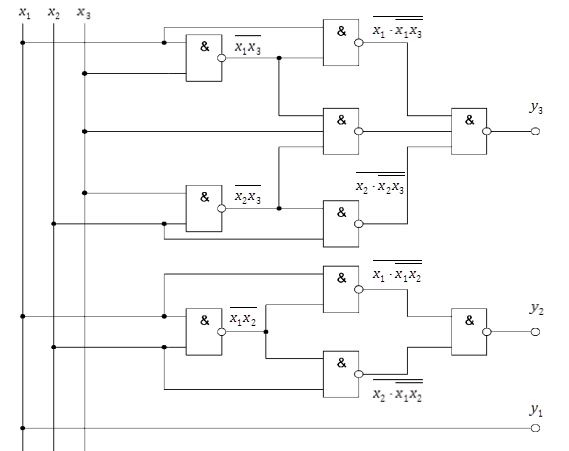
Получили готовое цифровое устройство —преобразователь трехразрядного кода из прямого в дополнительный.
Не знаю, насколько актуален вышеизложенный метод синтеза. Постарался все изложить на том уровне, на каком понимаю данную тему сам. Жду комментов от компетентных.
Литература:
Цифровые и аналого-цифровые устройства / А. В. Логинов, Ан. В. Логинов. ЛМИ, 1989
Автор: Sergeeff