Говорят, каждый программист должен в своей жизни написать хотя бы один компилятор или придумать какой-нибудь язык программирования. Дизайн нового языка — дело непростое, ведь нужно продумать десятки параметров, которые, как кубики Lego, должны хорошо между собой сочетаться. Одно неудачное решение может перечеркнуть судьбу языка, когда он еще даже не вышел в свет. Сотни языков прозябают в забвении, подвинутые с подиума старшими братьями, но мир с упорством, достойным лучшего применения, рождает ежегодно два-три новых. Попадут ли они хотя бы в «группу альтернативного мировоззрения», или даже станут мэйнстримными, покажет время. К счастью, моему языку это не нужно, поскольку на нем нельзя программировать, — им можно только любоваться. Ибо это язык визуализации Haskell-кода, о дизайне которого пойдет речь в статье.
Haskell — замечательный язык. Он очень выразительный и емкий. Код получается на порядок компактнее кода на императивных языках (C++, Java, C#), несмотря на то, что в нем меньше синтаксических конструкций. Чистая функциональная природа Haskell и его дизайн способствуют тому, что код становится похож на математическую запись. Возьмем для примера показательный (но не лучший) вариант факториала:
fact n | n == 0 = 1
| n > 0 = n * fact (n-1)
В этих двух строчках отлично узнается знакомая со школы рекуррентная формула факториала:
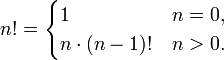
Конечно, определенный рекурсивно факториал не будет сильно хуже на любом другом языке, что может вызвать сомнения, а так уж ли Haskell выразителен.
int fact(int n)
{
if (n == 0) return 1;
return n * fact (n - 1);
}
Фокус в том, что обе функции написаны в функциональном стиле, поэтому между ними особой разницы и нет. Однако, пожалев стек, мы могли бы в императивном языке использовать цикл, что выглядит уже совсем по-другому:
int fact(int n)
{
int f = 1;
for (int i = 2; i <= n; ++i)
f *= i;
return f;
}
Программисты хорошо знают о том, что визуализировать последние два примера можно с помощью блок-схемы:
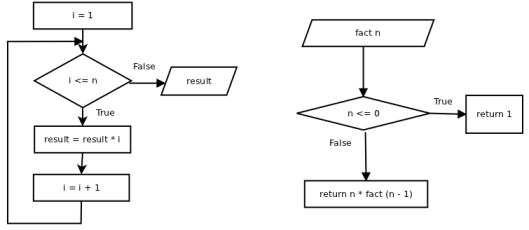
Вторая схема, в принципе, описывает, что происходит и в рекурсивном коде на Haskell. И хотя блок-схемы — это визуализация, они все-таки отличаются от того, что хочу я: они показывают, __что__ происходит, а не __как выглядит__. Я же хочу перенести код на трехмерную сцену, — так, чтобы сцена получилась красивой, интуитивной и по возможности необычной. Смысл визуализации есть в этом.
При дизайне языка приходится думать над тем, как его потом расширять. Сделаешь неверно или неудобно, — и новым затеям не будет места без того, чтобы разрушить обратную совместимость. Истории такие примеры известны; не миновала сия чаша даже некоторые очень популярные языки (например, Python 3.0, который не совместим с ранними версиями). В значительной мере на расширяемость дизайна влияют совсем малые вещи, так сказать, синтаксис в малом. При удачных детальках весь язык строится как один большой и хорошо продуманный конструктор. Haskell из таких, а значит, язык визуализации тоже должен держать марку. И тут я даже не могу сделать скидку на то, что дизайн Haskell известен, — мне все равно приходится преодолевать эти трудности с самого начала. Хотя в некотором смысле мне, конечно же, проще.
Итак, нужно продумать дизайн графического языка, достаточно самостоятельный, но при этом наглядный и эстетически полезный. Думать нужно над отдельными синтаксическими единицами, в то же время поглядывая на уровень выше — на их связь и на их значение в общей канве. Отталкиваясь от того самого факториала, я планирую когда-нибудь придумать эскизы даже для такого вот Haskell-кода:
-- | Collects actions for specified box side drawings.
-- | It should be used only in this module.
f :: PreparedTextureObjects
-> GLfVertex3
-> (BoxSide, QuadColorSpec)
-> ([BoxSide], [IO()])
-> ([BoxSide], [IO()])
f texRes boxDim (side, qColorSpec) (sList, ioList) = let
boxIO = do setQuadColorSpec texRes qColorSpec
GL.renderPrimitive GL.Quads (boxSide boxDim side)
in (side : sList, boxIO : ioList)
Или для такого:
data QuadColorSpec = QuadTexture TextureName
| QuadPlainColor GLfColor4
| NoQuadColorSpec
deriving (Show)
data ObjectTextureSpec = BoxTextureSpec
{ quadSideTexes :: [(BoxSide, QuadColorSpec)]
, defQuadSideTex :: QuadColorSpec
} deriving (Show)
data CornerCoord = UR | DR | DL | UL
deriving (Show)
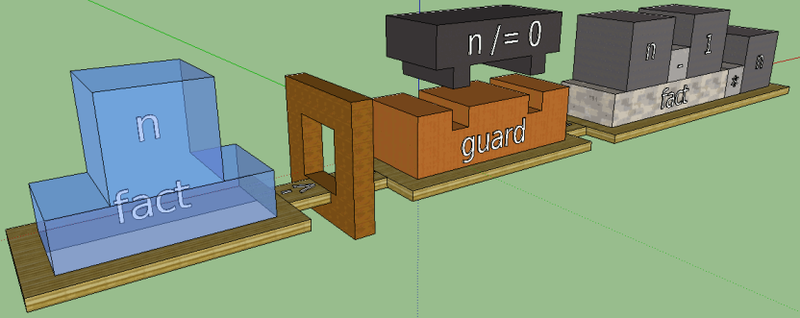
А пока у меня есть код факториала, с него и начинался язык визуализации:
fact n | n == 0 = 1
| n /= 0 = fact (n - 1) * n
Здесь мы видим несколько синтаксических конструкций:
| название функции | fact | |
| 2 охранных выражения | | n == 0 | |
| | n /= 0 | ||
| 2 тела функции | = 1 | |
| = fact (n — 1) * n |
В свою очередь, каждое тело функции разбивается на древовидное вычислительное выражение. Возьмем второй случай. Представляя элементы этого дерева в виде коробок, мы получим первый грубый вариант:
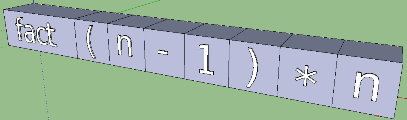
И сразу же проступают недостатки. Можно представить, как вырастет визуализация кода, если добавить в тело функции еще каких-нибудь действий и выражений. Да что там! Выражения могут сами состоять из выражений, и простое соотнесение каждого элемента с коробкой приведет к тому, что мы просто получим длинную и неинтуитивную цепь из коробок. Решение «в лоб» здесь не подходит. Вспомним полезный факт: явным воплощением древовидной конструкции является пирамида. Вычислительное выражение тоже можно представить в таком виде, причем даже несколькими способами:


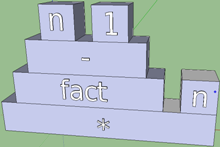
Последняя картинка субъективно симпатичнее за счет характерных пирамидальных выступов. Можно было бы остановиться на этой форме, но есть у бинарных функций особенность, что они могут быть операторами. Отличие операторов от функций чисто интуитивное, а с точки зрения языка это одно и то же, просто по-разному записывается — в функциональной и инфиксной записях:
isListElement x xs = elem x xs -- функциональная форма
isListElement’ x xs = x `elem` xs -- инфиксная форма
Операторы по умолчанию используются в инфиксной записи, но допустима и функциональная тоже:
add a b = a + b
add’ a b = (+) a b
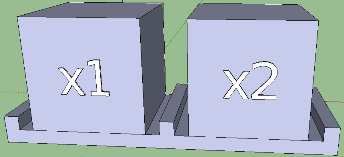
И этот факт можно легко отобразить при визуализации. На следующем эскизе помимо выделения инфиксной формы я увеличил конечные синтаксические единицы (переменные и константы) в два раза:
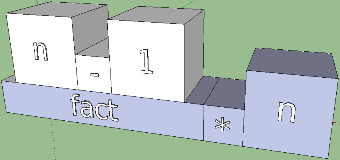
Уменьшилась высота пирамиды, что хорошо, и стало видно, где инфиксная запись, а где — функциональная. Такой подход становится полезен при задании идущих подряд вычислений:
add3 a b c = a + b + c
someF x y z = x >>= y >> z
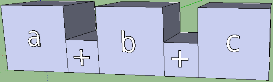

А для функций с большим числом аргументов стоит сохранить промежуток между коробками.
На эскизах видно, что длина коробок зависит от названия на коробке и от места, занимаемого аргументами. Тут уж ничего не поделаешь: надпись нужна, и уменьшать ее в размерах не стоит, иначе мы потеряем единообразие. Это на web-страничке или в документе каком-нибудь можно шрифты подгонять, а код должен выглядеть строго, потому что его так легче читать. Поэтому сложные, массивные вычислительные выражения будут выглядеть тоже внушительно. Посмотрим на функцию для чисел Фибоначчи:
fibs = 0 : 1 : zipWith (+) fibs (tail fibs)
Выглядит выражение (да и работает тоже!) очень красиво. Попробуем построить эскиз для него, помня о том, что знак “двоеточие”, использованный дважды, записан в инфиксной форме, а zipWith — это функция, принимающая три аргумента: (+), fibs и (tail fibs). Проблема здесь появляется с плюсом в скобках. Знак передается в другую функцию как аргумент, — и для Haskell это нормальное и очень полезное явление, известное как “функция высшего порядка”. Дополнительно, у оператора + откушены оба его собственных аргумента, — и это уже называется сечением. Согласно нашим прошлым правилам, оператор + должен стать конечным аргументом с увеличенной коробкой. В принципе, это нормально:
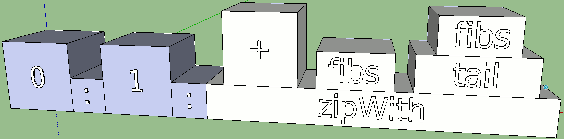
Но заглядывая в будущее, мы можем поразмышлять над тем, как в целом будут выглядеть сечения и каррированые функции. Возьмем для примера такой немного искусственный код:
ops = [(+), (*), (-)]
func x y op = x `op` y
result = map (func 2 3) ops
Здесь три функции: ops возвращает список операторов, func — производит над аргументами x и y действие, переданное как op, а внутри result это всё используется и что-то вычисляется. Если быть честным, при выполнении result вернет такой список: [5, 6, -1], и нетрудно проследить, как он получился. Функцией map функция (func 2 3) была применена ко всем операторам из списка ops. Нас в данном случае интересует, что (func 2 3) — это каррированая запись, у которой один аргумент остается вакантным. Операторы в скобках тоже каррированы (правильнее сказать — усечены), у них все уже украдено до нас… то есть, отобраны по два аргумента. В коде Haskell это никак не отражается, и странная запись вроде такой:
nullMap = map null
может ни о чем нам и не сказать, если не знать, что делают функции map и null, и если сигнатуры типов не указаны. Однако в визуализации мы могли бы чётко показать, что эти функции требуют еще какие-то аргументы. Достаточно постулировать, чтобы аргументы помещались в пазы функций, и количество пазов соответствовало арности. Вот результат для функций result и nullMap:
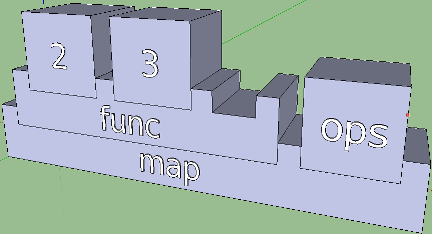
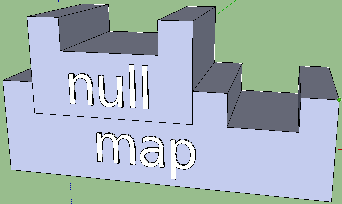
При дизайне вычислительных выражений еще остается существенным вопрос о пропорциях, и тут возможен тотальный разгул фантазии. Параметризации поддаются высота элементов, расстояние между аргументами, длина и глубина пустого паза, высота и длина конечных элементов, размер пирамидального отступа. Если же вооружиться знаниями о гармонии то, наверное, стоит внести в пропорции магическое золотое сечение. Оно всё делает лучше!
Важной конструкцией любого языка являются условные переходы. В Haskell оператор if тоже есть, и он таков, что оператор else обязательно должен ему сопутствовать. Не может быть выражения, у которого одна из альтернатив отсутствует, — в мире, где всё есть функция, результат должен возвращаться всегда. Ниже представлено вычисление факториала с if (мы, как и в прошлый раз, не задумываемся о том, что n может прийти отрицательный):
fact n = if n == 0 then 1 else fact (n - 1) * n
Форматировать код здесь можно по-всякому. then и else не чувствительны к отступам и могут быть расположены на новой строке (только отсчитывая хотя бы один пробельный символ от функции fact):
fact n = if n == 0
then 1
else fact (n - 1) * n
Возможно, эти перестановки как-то помогут придумать дизайн данной конструкции. Наивный перенос слов if, then и else как самых нижних слоев пирамид, несколько пересекается с прошлым вариантом и сбивает с толку. Но вот если разделить их каким-нибудь обособленным элементом, получится уже интереснее. Сравните два следующих варианта:
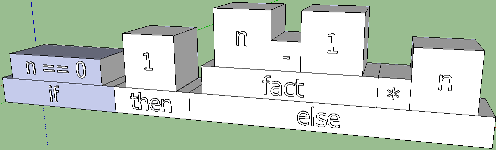
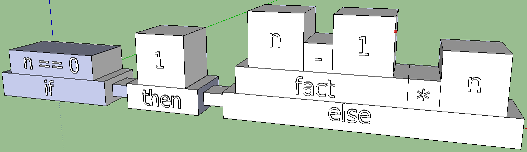
Давая волю фантазии, можно добиться некоторой интуитивности последнего варианта. Ведь что такое if? Это когда булевое выражение проверяется на истинность, то есть, на совпадение с True. На принципе совпадения построены конструкторы, паззлы и кое-что ещё: есть совпадение, — штырь подходит к пазу; нет совпадения, — ну, извините… Попробуем внести эту концепцию в эскиз:
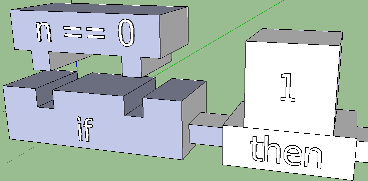
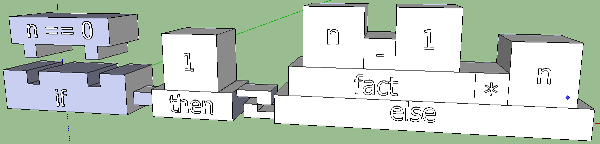
Выглядит интересно и побуждает фантазировать дальше. Можно экспериментировать с положением, формой, размерами, но нужно не забывать о том, что if-then-else — это выражение, и оно будет использоваться внутри других выражений. То есть, раз уж мы ограничиваем себя в пространстве ради выразительности, то и условный оператор не должен выходить за некие эмпирические рамки.
Возможно, для if-then-else это и не трудно, и эти синтаксические элементы, как паиньки, поместятся в любой части выражения, но вот родственная case-конструкция может доставить хлопот. Она умеет расширяться: количество альтернатив ничем не ограничено. Перепишем функцию факториала:
fact n = case n == 0 of
True -> 1
False -> fact (n - 1) * n
Есть над чем подумать. В case-конструкции добавляется новая семантика: сопоставление с образцом. Тут я, признаться, еще не придумал достойного варианта. Но можно попробовать по аналогии с одним из последних эскизов if:
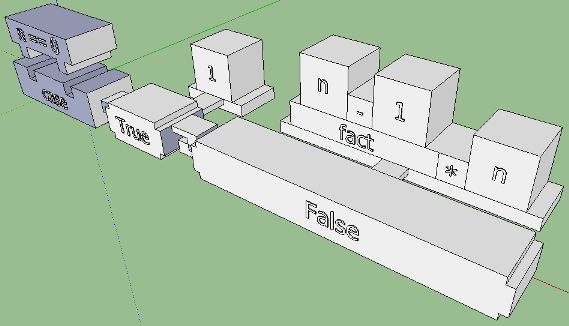
Смысл сопоставления с образцом в том, что на каждом из кубиков перед знаком "->" может быть достаточно большое выражение. Возможности огромны: здесь и расщепление списков, и сколь угодно глубокое сопоставление с алгебраическими типами данных, и даже — с подключенным расширением языка View Patterns — некий синтаксис, напоминающий функции. Я покажу лишь простой, достаточно типичный код, где используется pattern matching внутри case:
toHabrFormat (s, (ch:[])) = s ++ [ch]
toHabrFormat a@(s, b@(ch:inStr)) = let formatted = (foldr1 (<|>) formatters) a
in case formatted of
Just (res, []) -> res
Just (res, (r:rs)) -> toHabrFormat (res ++ [r], rs)
Nothing -> toHabrFormat (s ++ [ch], inStr)
Видимо, пока нет ясности о том, как представлять алгебраические типы данных, списки, кортежи и прочее — case-конструкция будет неубедительной.
Сейчас, всё же, отложим в сторону вычислительные выражения и попробуем завершить визуализацию функции факториала с её именем и охранными выражениями.
fact n | n == 0 = 1
| n /= 0 = fact (n - 1) * n
Об охранных выражениях есть что сказать. Это обычные выражения, но возвращают они всегда булевое значение — True или False. Они служат некими фильтрами, как бы не пропуская выполнение в тело, если условие не истинно. Играя с этой концепцией, можно придумать что-то вроде пресловутого if. Оценим следующий вариант:

Коробка с равенством (”мост”) появилась из желания соединить охранные выражения и тело функции так же, как в коде. И это, кажется, интересная идея. Развиваясь, она переросла в нечто большее — в визуальное разделение частей (имя функции; охранные выражения; вычислительное выражение). Можно пойти дальше: поместить их на платформы, очертив тем самым пространство каждой из частей.
В коде охранное выражение начинается с символа ‘|’. Если бы его не было, код выглядел бы противоречиво:
fact n n == 0 = 1
n /= 0 = fact (n - 1) * n
Компилятор бы не понимал, чем являются буквы и символы после слова fact. Вертикальная черта — необходимый элемент синтаксиса, и поэтому нам нужно его внести в визуализацию. Логично поставить что-нибудь слева от платформы с булевым выражением; это может быть, например, “стена”:
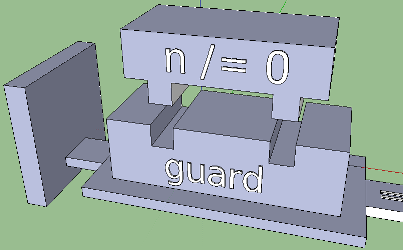
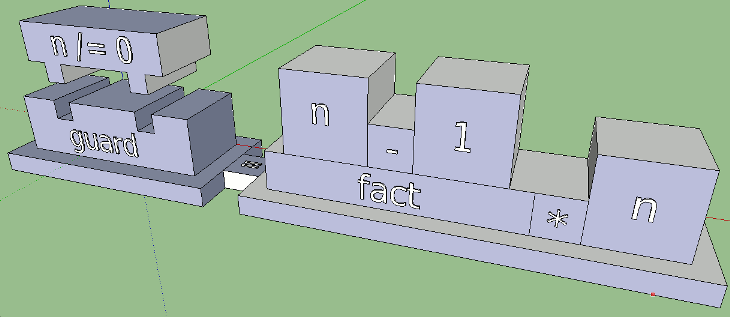
Но так ли это интуитивно? Сплошная коробка выглядит препятствием, запретом, а нам нужны — условие, вариативность. Если мы представим ход выполнения в виде кубика, то он, двигаясь от имени функции к охранному выражению, просто столкнется со стеной, — и ни одно из тел функции не будет достигнуто. В этом размышлении кроется ключ к более интуитивному варианту: а что если сделать в стене отверстие? Можно мыслить себе так: если логическое условие истинно, кубик пройдет сквозь отверстие и попадет, куда нужно. Направление движения тоже стоит визуализировать: пусть его показывают мосты со стрелками, — они также помогут соединить правую и левую часть функции:

Гораздо лучше! Теперь визуализируем имя функции с аргументами. Опять же, здесь мы имеем дело с pattern matching, и, по-хорошему, его стоило бы совместить с арностью. Вырезы для аргументов мы уже научились делать, они пригодятся и здесь. Без сопоставления с образцом у нас был бы такой вариант:
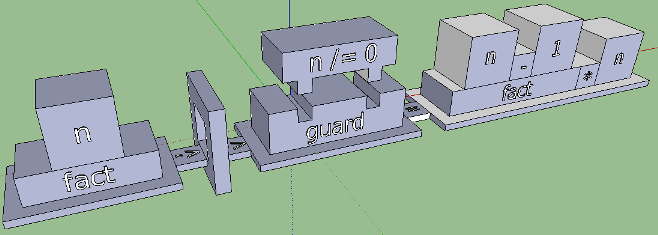
Итак, построена основа графического языка, и мы теперь примерно представляем, как он должен выглядеть. Для ясной картины еще нужно разобраться с такими важными вещами, как алгебраические типы данных, списки, кортежи и сопоставление с образцом. Когда с ними будет покончено, скорее всего появятся идеи, что делать с декларациями типов, с do-конструкциями, генераторами списков, as-образцами, типами классов, воплощениями классов и прочими замечательными элементами Haskell-синтаксиса.
Начнем с алгебраических типов данных, списков и сопоставления с образцом. Выше в примере с case мы уже попробовали визуализировать АТД и pattern matching. Представим, что арность вместо вырезов обозначается выступами. Картинка с case, True и False тогда будет неверной, потому что у этих двух конструкторов арность равна нулю. Однако, арность Just равна 1, — и у него будет один выступ.

Списки создаются через инфиксный оператор ":". Мы уже умеем его визуализировать. Возьмем более сложный случай, — когда есть и «неважные» элементы, и пустой список. Вот гипотетический код:
someFunc someList = case someList of
(x1:x2:_:xs) -> Just (x1, x2)
(x1:[]) -> Just (x1, x1)
[] -> Nothing
Уже сами конструкции языка Haskell наглядно показывают свою суть. Неважный аргумент заменяется знаком подчеркивания, а пустой список — пустыми квадратными скобками. Учтем это при визуализации. Не видно в формализме кода только различий между аргументами x1, x2 и xs из первой альтернативы. Между тем, x1 и x2 — это отщепленные спереди элементы списка, а xs — это весь остальной возможно пустой список. Полезно было бы разницу как-то показать.
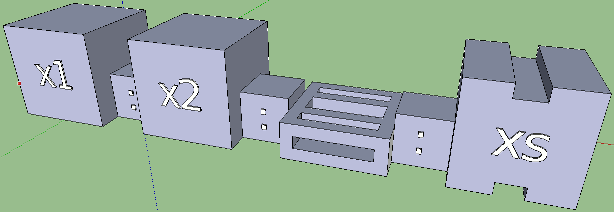

Да, списки выглядят очень. Особенно мне нравится «неважный» элемент. А что насчет кортежей? Ну, мудрить незачем: просто поместим каждый элемент кортежа в паз на общей доске. С функцией спутать нельзя, так как у кортежа нет имени, и его основание тоньше. Для надежности можно изменить цвет.
Не такая уж и трудная задача оказалась! Вот так, логически рассуждая, можно построить язык для визуализации. Ничего страшного, если какие-то конструкции будут изменены до неузнаваемости через несколько версий. Сейчас, не затронув то, как визуализировать декларацию типов, я рискую потом обнаружить, что они не вписываются в полуготовую схему. Придется что-нибудь изменять, чем-нибудь жертвовать, но общие принципы визуализации останутся прежними. Конечно, для фантазии остались огромные просторы. Я еще не подбирал цвета и оттенки, не думал над шрифтами, да и форма элементов может быть улучшена во многих смыслах. Была даже такая идея: коробки с надписями сделать стеклянными, а надпись поместить внутрь, и заставить это всё переливаться отраженным светом. Увековечить, так сказать, код в стекле. Наверное, получилось бы что-то вроде этого:

Красота, что и говорить. И уже кажется, что основные затраты здесь — на выдумывание дизайна, а визуализацию можно быстро состряпать в каком-нибудь графическом редакторе, но… В реальности всё несколько сложнее, потому что для визуализации нужна программа, а не статичная 3D-сцена. Именно такую программу я и создаю в проекте «GraphServer». Задача осложняется тем, что не для всех конструкций я придумал визуализацию; уже при написании этой статьи были сильно изменены или изобретены некоторые конструкции. Но даже то, что готово на данный момент, выглядит многообещающе.
Это кросс-статья. О создании сервера визуализации читайте в статье «Haskell — Эстетика».
P.S. Прошу прощения за не совсем качественные картинки. Habrastorage, похоже, с ними что-то делает.
Автор: graninas