Поиск таинственной математики, на которой основана фигура в iOS

Это история о том, как один инженер Figma искал идеальный ответ на программистскую задачу.
В знаменитом интервью 1972 года Чарльз Имз кратко ответил на несколько фундаментальных вопросов о природе дизайна. Отвечая на первый вопрос, он определил дизайн как «план компоновки элементов для достижения определённой цели».
Остальные ответы тоже очень лаконичны, вплоть до метафор. Но когда Имза спросили о роли ограничений дизайна, он остановился и выдал самый длинный и самый продуманный ответ за всё интервью: «Один из немногих эффективных ключей к проблеме дизайна — это способность дизайнера распознавать как можно больше ограничений; его готовность и энтузиазм к работе в этих ограничениях».
Хотя я не дизайнер по профессии — я разработчик Figma, веб-инструмента совместного проектирования — несложно заметить, что замечания Имза относятся и к моей работе. Вместо элементов UI я выраженные в коде компоную математические концепции для создания инструментов и функций. И ограничения времени, простоты, поддержки и даже эстетики играют похожую доминирующую роль в моей работе.
Один недавний проект особенно хорошо подчёркивает эти параллели. Мне поручили каким-то образом добавить в Figma поддержку фигуры Apple с причудливым названием «квадрокруг» (squircle). Я начал изучать тему.
Исследование превратилось в настоящую математическую Одиссею, полную фальстартов, скрытых проблем, возникающих ограничений, разведки, напряжения — и разрешения. Короче говоря, это была история, которую в какой-то степени переживает каждый дизайнер почти каждый день.
Чтобы доставить удовольствие подобным мне математическим вундеркиндам и показать весь процесс проектирования с использованием математики, далее описан каждый шаг: от первого квадрата до окончательного результата.
Квадрокруг: оператор закругления
История началась задолго до того, как я основал Figma, а именно 10 июня 2013 года — в день выхода iOS 7. В новой ОС было некое едва заметное обновление: иконки приложений на главном экране стали более сочными, более органичными. Вместо квадрата с закруглёнными углами каждая иконка превратилась в квадрокруг (squircle, сочетание слов «квадрат/прямоугольник» и «круг»).
Вы спросите, какая разница? Если честно, то небольшая: за основу взят обычный прямоугольник со скруглёнными углами, но он немного обработан напильником в местах начала закруглений. Поэтому переход от прямой к изогнутой линии становится менее резким.
Если точно сформулировать на языке математики, то у квадрокруга непрерывная кривизна периметра, а у округлённого квадрата — нет. Это может показаться тривиальным, но подсознательно действительно оказывает большое влияние: квадрокруг не похож на обработанный квадрат; он воспринимается как отдельная правомочная сущность, как форма гладкого камушка на дне реки — единое и элементарное целое.
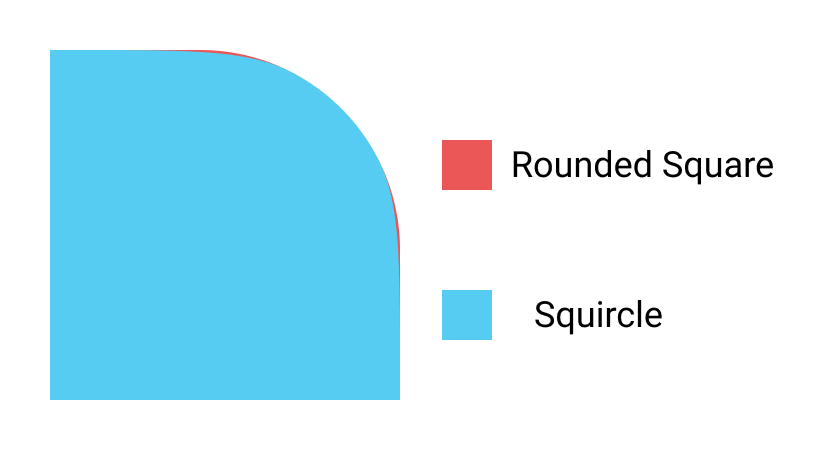
1.1. Сравнение округлого квадрата и квадрокруга: очевидно, разница невелика
Промышленным дизайнерам давно известно, насколько важны закругления для восприятия объекта. Внимательно посмотрите на углы Macbook или на ольдскульный футляр для проводных наушников под настольной лампой. Обратите внимание, как трудно найти положение, при котором углы бросают резко контрастные блики.
Причина в непрерывности закруглений, которые специально рассчитаны дизайнерами. Неудивительно, что именно компания Apple, которая имеет уникальный опыт разработки одновременно и программного, и аппаратного обеспечения, в конечном итоге применила идеи промышленного проектирования в дизайне интерфейсов, сделав свои иконки похожими на физические вещи собственного производства.
От формы к формуле
Конечно, мы в Figma любим дизайнеров iOS и считаем, что у наших пользователей всегда под рукой должны быть нужные элементы платформы. Чтобы предоставить им доступ к этой новой форме при проектировании, нужно найти точное математическое описание. Тогда мы начнём выяснять, как встроить эту форму в наш инструмент.
К счастью, люди задаются таким вопросом с момента выхода iOS 7. Конечно, мы не первые, кто пошёл по этому пути! Исходная фундаментальная работа Марка Эдвардса содержала скриншот с указанием, что форма иконки представляет собой особое обобщение эллипса под названием суперэллипс. Следующая математическая формула описывает круги, эллипсы и суперэллипсы в зависимости от выбора a, b и n:
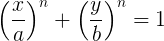
2.1. Формула суперэллипса
Скажем, если выбрать n = 2, a = 5 и b = 3, то получится нормальный эллипс с большими полуосями 5, ориентированными вдоль оси x, и малыми полуосями 3, ориентированными вдоль y. Если оставить n = 2 и выбрать а = b = 1, то получится идеальная окружность единичного радиуса. Но если выбрать n больше двух, то получится суперэллипс — округлая эллиптическая форма, которая начинает сливаться с формой прямоугольника, в который она вписана, где углы становятся идеально прямыми, если n стремится к бесконечности. Изначально предполагалось, что Apple выбрала форму с n = 5. Если вы попробуете такую формулу, то увидите, что она действительно очень близка к той, что используется в iOS 7+.
Если бы истинное описание действительно было таковым, то мы могли бы просто применить некое разумное количество кривых Безье — а затем аккуратно интегрировать новую концепцию в Figma. Но к сожалению, тщательный последующий анализ показал, что формула суперэллипса не совсем подходит (хотя в наши дни истинные суперэллипсы действительно используются в качестве других иконок). Фактически, для всех вариантов n в вышеприведённом уравнении есть малое, но систематическое несоответствие по сравнению с реальной формой иконки.
Это первый тупик в истории: у нас есть элегантное простое уравнение для чего-то очень похожего на квадрокруг iOS, но оно принципиально неверное. Но мы обязаны дать нашим пользователям верное уравнение.
Продвижение вперёд требует серьёзных усилий, и я снова рад собрать урожай, посеянный другими. Один исследователь Майк Свонсон из Juicy Bits выдвинул гипотезу, что углы квадрокруга построены на последовательности кривых Безье. Он применил генетический алгоритм для оптимизации сходства с официальной формой Apple. Полученные результаты соответствуют оригиналу, как доказано отличным прямым сравнением Манфреда Швинда, который изучил код iOS, непосредственно генерирующий иконки. Таким образом, у нас есть два разных подхода, дающих одинаковую структуру кривых Безье: квадрокруги iOS 7 взломаны и дважды проверены независимыми исследователями, и нам даже не нужно ничего вычислять!
Напильник в действии
Остаются две важные детали, мешающие нам клонировать форму непосредственно в Figma.
Во-первых, удивительный факт, что версия формулы iOS (по крайней мере, во время исследования) сделана с некоторыми причудами — углы не совсем симметричны, а с одной стороны есть крошечный прямой сегмент, который явно здесь не должен быть. Нам он не нужен, потому что усложняет и код, и тесты, го его легко удалить простым зеркалированием половины угла, где баг отсутствует.
Во-вторых, при выравнивании соотношения сторон реального прямоугольника из iOS форма иконки резко меняется от нужного нам квадрокруга до совершенно иной формы. Дизайнерам будет неприятен такой выверт, и он заставляет чётко определить, какие формы «должны» проявляться при определённых условиях.
Наиболее естественным и полезным поведением при выравнивании квадрокруга стало бы постепенное исчезновение сглаживания до тех пор, пока не останется места для перехода между круглой и прямой частями угла. Дальнейшее выравнивание должно уменьшить радиус закруглённой секции, что соответствует нынешнему поведению Figma. Формула квадрокруга Apple здесь мало нам помогает, потому что в ней закругление выполняется фиксированным образом: она не дает указаний, как приближаться или удаляться от старого прямоугольника с закруглёнными углами. Что нам действительно нужно, так это параметризуемое скругление, где определённое значение параметра очень близко соответствует форме Apple.
В качестве дополнительного бонуса, если мы cможем параметризовать превращение прямоугольника c закруглёнными углами в квадрокруг, то вполне можем применить такой же процесс в других местах Figma, где используется закругление: звёзды, многоугольники и даже углы в произвольных векторных сетях, нарисованных от руки. Несмотря на сложность, это начинает выглядеть гораздо более законченной и ценной фичей, чем просто добавление квадрокруга iOS 7. Теперь мы даём дизайнерам бесконечное разнообразие новых форм для использования во многих ситуациях, и одна из них соответствует иконке квадрокруга, с которой всё и началось.
Требование, чтобы наша схема закругления квадрокруга плавно регулировалась, но при этом соответствовала форме iOS 7 в определённой удобной точке из диапазона регулировки — это первое возникшее ограничение в нашей истории, и его трудно удовлетворить. Для балерины аналогичной задачей стало бы спроектировать целый прыжок по одной фотографии в полёте, чтобы в определённый момент фаза прыжка соответствовала фотографии. Звучит чертовски тяжело. Так может всё-таки понадобится какой-то расчёт?
Мощный инструмент: дифференциальная геометрия плоских кривых
Прежде чем погрузиться в параметризацию квадрокругов, отступим на шаг и сдуем пыль с некоторых формальных инструментов, которые помогут нам проанализировать происходящее. Прежде всего надо определиться, как описывать квадрокруг. Раньше в случае суперэллипсов мы использовали уравнение с x и y, где все точки (x, y) на плоскости, удовлетворявшие условиям уравнения, выводили суперэллипс. Это элегантно в случае простого уравнения, но реальные квадрокруги — это лоскутное одеяло соединённых вместе кривых Безье, что ведёт к неуправляемому нагромождению уравнений.
С этим осложнением можно справиться, используя более явный подход: возьмём одну переменную t, ограничим её конечным интервалом и сопоставим каждое значение t в этом интервале с отдельной точкой на периметре квадрокруга (на самом деле кривые Безье почти всегда представлены таким образом). Если сконцентрироваться только на одном из углов, тем самым ограничивая наш анализ изогнутой линией с чётким началом и концом, то можно выбрать такое отображение между t и углом, чтобы t = 0 соответствовало началу линии, t = 1 соответствовало концу линии, а плавное изменение t от 0 до 1 плавно вычерчивало закруглённую часть угла. На математическом языке опишем наш угол кривой r(t), которая структурирована как
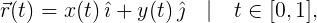
4.1. Биекция плоской кривой с [0,1]
где x(t) и y(t) являются отдельными функциями t для x и y компонентов r. Можем представить r(t) как своеобразную историю пути, скажем, вашей поездки на машине. Для каждого момента времени t между отправлением и прибытием вы можете оценить r(t) и получить положение вашего автомобиля на маршруте. Из пути r(t) можно вывести скорость v(t) и ускорение a(t):
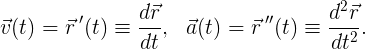
4.2. Скорость и ускорение плоской кривой
Наконец, математическая кривизна, которая играет главную роль в нашей истории, в свою очередь может быть выражена в терминах скорости и ускорения:
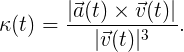
4.3. Беззнаковая кривизна плоских кривых
Но что на самом деле означает эта формула? Хотя это может выглядеть немного усложнённой, у искривления простая геометрическая конструкция, первоначально из-за Коши:
- Центр кривизны C в любой точке P вдоль кривой лежит на пересечении линии нормали к кривой в P и другой линии нормали, взятой бесконечно близко к P. (В качестве примечания, окружность с центром в C, называется соприкасающейся окружностью (osculating circle) в P, от латинского глагола osculare, что означает «поцелуй». Разве это не замечательно?)
- Радиус кривизны R — это расстояние между С и P.
- Кривизна κ является обратной величиной к R.
Как показано выше, кривизна κ неотрицательна и не различается поворотами вправо или влево. Поскольку нам важно такое отличие, то мы формируем из κ знаковую кривизну k, назначая положительный знак, если кривая поворачивает вправо, и отрицательный знак, если влево. Эту концепцию тоже можно сравнить с вождением автомобиля: в любой точке t знаковая кривизна k(t) — это просто угол, на который поворачивается рулевое колесо в момент времени t, со знаком плюс для поворота вправо и минус для поворота влево.
Геометрия рулит: параметризация длины дуги
С введением кривизны осталось уладить только несколько деталей. Во-первых, представим на мгновение два автомобиля, движущиеся по углу квадрокруга; один автомобиль резко ускоряется, а потом всё время тормозит, а другой равномерно газует до самого конца. Эти два разных способа вождения породят весьма разные истории пути, даже с одинаковой траекторией. Нас волнует только форма угла, а не способ её достижения, так как их привести к общему знаменателю? Здесь главное при пометке точек истории использовать не время, а совокупное пройденное расстояние, то есть длину дуги. То есть вместо вопроса «Где находилась машина через десять минут пути?» лучше отвечать на вопрос «Где находилась машина через десять миль от начала поездки?». Такой способ описания траектории фиксирует только геометрию и ничего более.
Если у нас есть некоторая история пути r(t), мы всегда можем извлечь длину дуги s как функцию времени t пути, проинтегрировав скорость следующим образом:
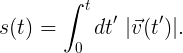
5.1. Интеграл длины дуги
Если мы можем инвертировать это отношение и найти t(s), то можем подставить её вместо t в нашей истории пути r(t), чтобы получить желанную параметризацию длины дуги r(s). Параметризация длины дуги для пути эквивалентна истории пути автомобиля, движущегося с единичной скоростью, поэтому неудивительно, что скорость v(s) всегда является единичным вектором, а ускорение a(s) всегда перпендикулярно скорости. Следовательно, в варианте с параметризацией по длине дуги описание кривизны упрощается только до величины ускорения.
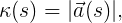
5.2. Кривизна в варианте с параметризацией по длине дуги
И можно установить соответствующий правый или левый знак, чтобы сформировать подписанную кривизну k(s). Очевидно, бóльшая часть осложнений в более общем определении кривизны заключалась просто в негеометрическом содержании истории пути. В конце концов, кривизна — чисто геометрическая величина, поэтому очень приятно видеть, что она выглядит простой в геометрической параметризации.
Спроектировать кривизну, вычислить кривую
Теперь о другой детали. Мы только что разобрались, как перейти от описания истории пути r(t) к описанию по параметру длины дуги r(s) и как извлечь из неё знаковую кривизну k(s). Но можем ли мы сделать обратное? Спроектировать профиль кривизны — и из него вывести родительскую кривую? Давайте ещё раз рассмотрим аналогию с автомобилем: предположим, что когда мы ехали на постоянной единичной скорости по всему маршруту, то фиксировали положение рулевого колеса непрерывно на протяжении всего пути. Если возьмём эти данные рулевого управления и потом передадим другому водителю, сможет ли он полностью восстановить маршрут, если правильно воспроизведёт позиции рулевого колеса и будет ехать точно на такой же скорости? Интуитивно у нас достаточно информации, чтобы восстановить родительскую кривую, но как это вычисление выглядит математически? Хотя немного шероховато, но такое возможно благодаря Эйлеру с помощью параметризации длины дуги. Если мы выберем такую систему координат, чтобы кривая начиналась в начале координат и изначально направлялась вдоль оси x, тогда x(s) и y(s) можно восстановить из k(s) следующим образом:
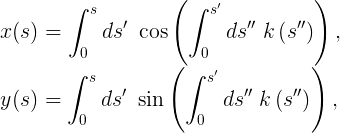
6.1. Восстановление кривой по её кривизне
Наконец, обратите внимание на аргумент синусной и косинусной функций: это интеграл знаковой кривизны. Обычно у тригонометрических функций в качестве аргументов указываются углы в радианах. Так и есть в нашем случае: интеграл от a до b подписанный кривизны — это курс в b минус курс в a. Таким образом, если взять прямоугольник и закруглить угол как угодно, измерить кривизну закруглённой части и интегрировать результат, в итоге мы всегда получим π/2.
Анатомия квадрокруга
Разобравшись с деталями, применим эти аналитические инструменты к некоторым реальным формам. Начнём с закруглённого угла прямоугольника, с радиусом угла равным единице. Построим сначала сам угол, а затем кривизну как функцию длины дуги:
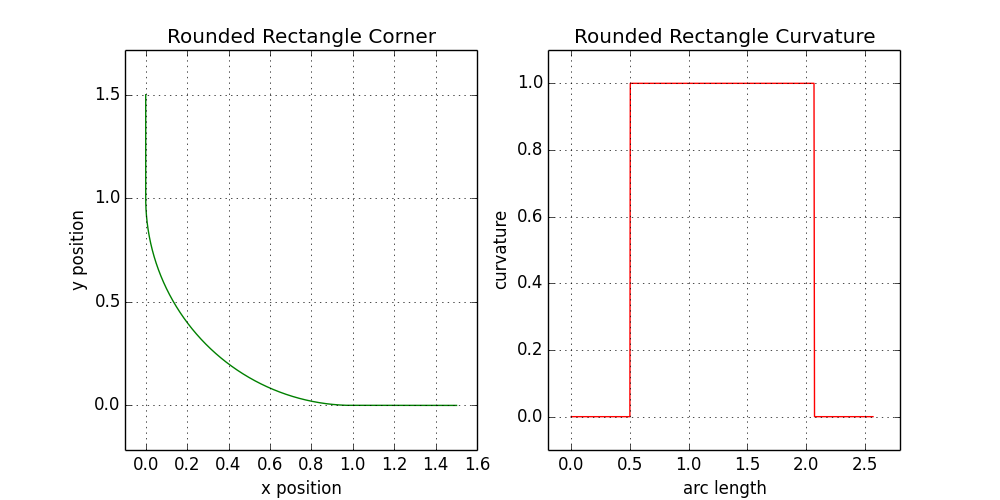
7.1. Анализ кривизны закруглённого прямоугольника
Теперь повторим процесс для углов реальных квадрокругов Apple — и увидим, что их кривизна сильно отличается:
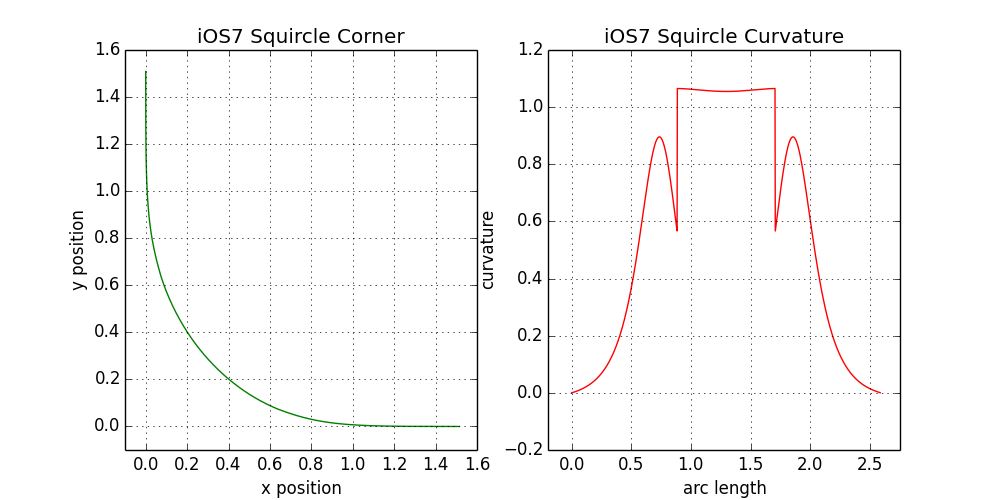
7.2. Анализ кривизны квадрокруга iOS 7
Кривизна выглядит довольно зубчатой, но это необязательно плохо. Как мы увидим позже, можно найти компромисс между плавным графиком кривизны и небольшим количеством кривых Безье, а в угле iOS их только три. Как правило, дизайнеры готовы пожертвовать математически идеальным профилем кривизны ради уменьшения количества кривых Безье. Отбросив детали, на правом графике проявляется общая картина: кривизна поднимается вверх, выравнивается посередине, а затем возвращается вниз.
Прорыв: параметризованное сглаживание
Бинго! В этом последнем наблюдении лежит ключ к тому, как параметризовать сглаживание угла нашего квадрокруга. При нулевом сглаживании профиль кривизны будет как у закруглённого прямоугольника: в форме столешницы. По мере постепенного усиления сглаживания высота столешницы остаётся неизменной, но её края превращаются в крутые наклоны, образуя профиль равнобедренной трапеции (конечно, по-прежнему с общим углом π/2). Когда сглаживание приближается к максимуму, плоская часть трапеции исчезает — и мы получаем широкий равнобедренный треугольник, высота которого соответствует высоте первоначальной столешницы.
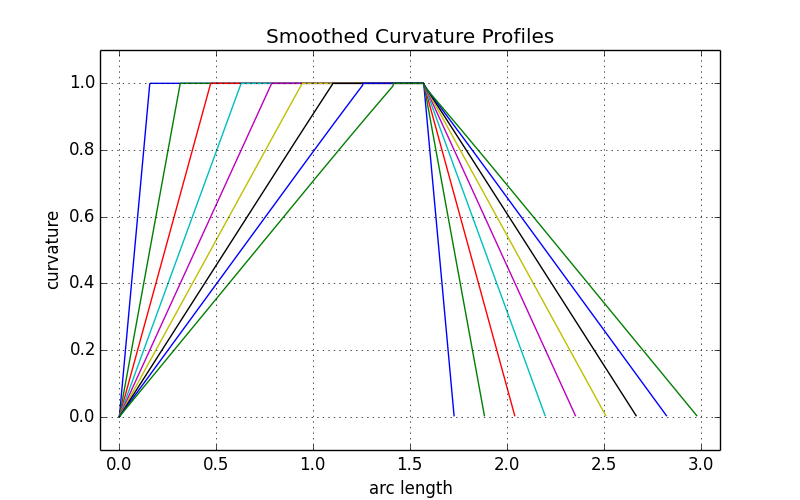
8.1. Профили кривизны для различных значений параметра сглаживания
Попробуем выразить этот набросок профиля кривизны в математических терминах, используя ξ как параметр сглаживания, который изменяется от нуля до единицы. Чтобы предусмотреть использование с другими формами, где нет прямых углов, введём также угол поворота θ, который в случае прямоугольника равен π/2. Соединив их вместе, можно выразить кусочно-непрерывную функцию в трёх частях: одна для подъёма кривизны, вторая для плоской вершины и третья для спуска:
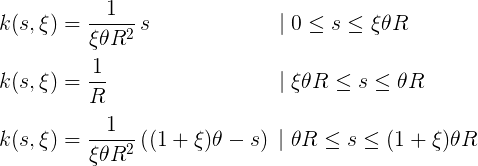
8.2. Параметризация профиля кривизны квадрокруга
Обратите внимание, что первая и третья части (подъём и спуск) исчезают при приближении ξ к нулю, а средняя часть (плоская вершина) исчезает при приближении ξ к единице. Выше мы показали, как перейти от профиля кривизны к родительской кривой. Попробуем сделать это на первом уравнении, описывающем линию, кривизна которой начинается с нуля и неуклонно увеличивается. Сначала сделаем простой внутренний интеграл:
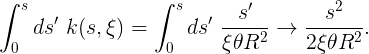
8.2. Первый интеграл из 6.1 применительно к уравнениям 8.2
Пока что всё отлично! Можно продолжить и сформировать следующую пару интегралов:
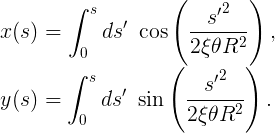
8.2. Второй интеграл из 6.1 применительно к уравнениям 8.2 (интеграл Френеля)
Увы, здесь мы попали в затор, потому что эти интегралы не такие простые. Если вы слышали о связи между тригонометрическими функциями и экспонентами, то можете догадаться, что эти интегралы связаны с функцией ошибки, которую нельзя выразить элементарными функциями. То же самое относится и к этим интегралам. Так что будем делать? Решение выходит за рамки этой статьи (см. этот пост на Math StackExchange для подсказки), но в данном случае можно заменить синус и косинус в степенных рядах, а затем поменять сумму и интеграл:
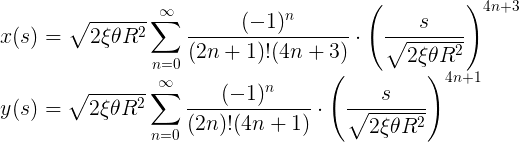
8.4. Разложение в ряд интегралов Френеля
Степенные ряды кажутся почти непроходимыми, так что давайте сделаем ещё шаг и явно выпишем первые несколько элементов в каждом ряду, перемножив всё для упрощения. Это даёт следующие несколько элементов для x и y формы:
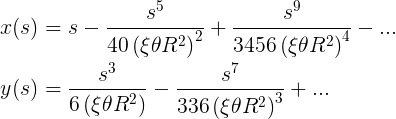
8.5. Элементы низкого порядка (n < 3) из 8.3
Апофеоз клотоиды
Вот это уже конкретный результат! Мы можем реально начертить график этой пары уравнений (при разумном выборе ξ, θ и R) — и получить контур как функцию от s. Если бы у нас было произвольное количество элементов и возможность вычислить суммы, то мы бы увидели, что по мере возрастания s кривая закручивается в спираль, хотя это происходит далеко от интересующей нас области.
Повторяя тезис из начала этой статьи, мы опять не первые, кто занимается такими исследованиями. По причине линейной кривизны, которая очень полезна на практике, многие натыкались на эту кривую в прошлом. Она известна как спираль Эйлера, спираль Корню или клотоида — и широко используется при проектировании треков, в том числе автомобильных дорог и американских горок.
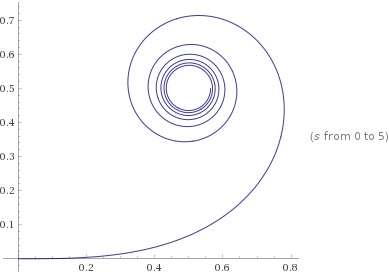
9.1. Клотоида до s = 5
Если использовать разложение только до n < 10, как указано в 8.5, то у нас наконец-то есть всё необходимое, чтобы произвести первый артефакт. Этот ряд представляет собой восходящую (первую) часть уравнения 8.2, но его легко адаптировать к нисходящей (третьей) части, и мы свяжем эти части между собой дуговым сегментом для плоской (второй) части. Такой метод обеспечивает математически идеальный угол квадрокруга, который точно соответствует конструкции кривизны, впервые представленной в уравнениях 8.2. Вот анализ кривизны, проведённый на клотоиде для угла квадрокруга с ξ = 0,4:
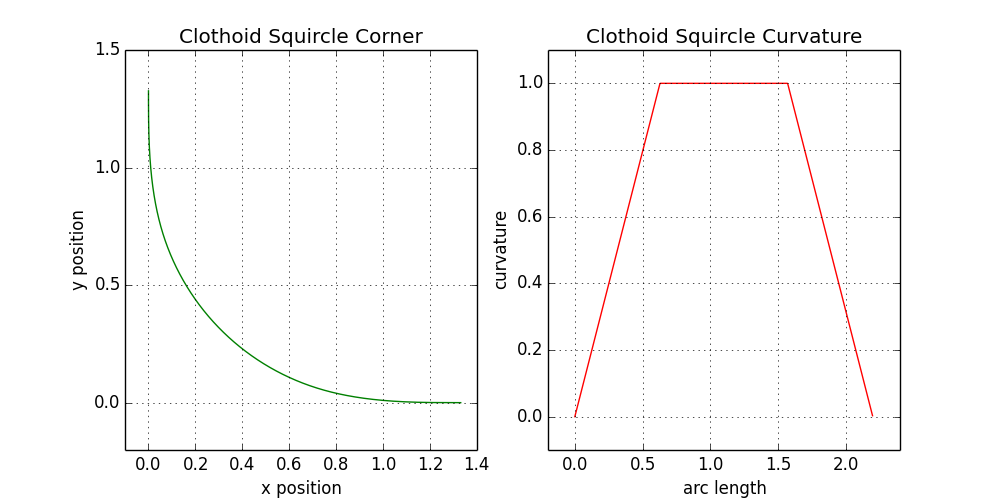
9.2. Угол квадрокруга при ξ = 0,4 при использовании клотоид девятого порядка и дуг окружностей
Хотя приятно получить такую элегантную форму, но следует понимать, что это лишь идеальная версия. Такая точная форма не подойдёт по нескольким причинам. Из них главная причина в том, что центр кривизны круговой части перемещается как функция параметра сглаживания ξ — в идеале он был бы зафиксирован.
Ещё важнее, что степень длины дуги s в определённых нами условиях может достигать девяти. В Figma все непрерывные кривые должны быть представимы кубическими кривыми Безье (частные случаи которых — квадратичные кривые Безье и линии). Это ограничивает нас сохранением только кубических и членов нижнего порядка. То есть каждый из приведённых выше рядов для x(s) и y(s) будет усечён до одного элемента. Трудно надеяться, что после такого усечения сохранятся необходимые свойства фигуры.
К сожалению, недостаточно отбросить члены более высокого порядка, ибо полученная конструкция очень плохо работает при больших значениях ξ. На рисунке внизу показан результат для ξ = 0,9:
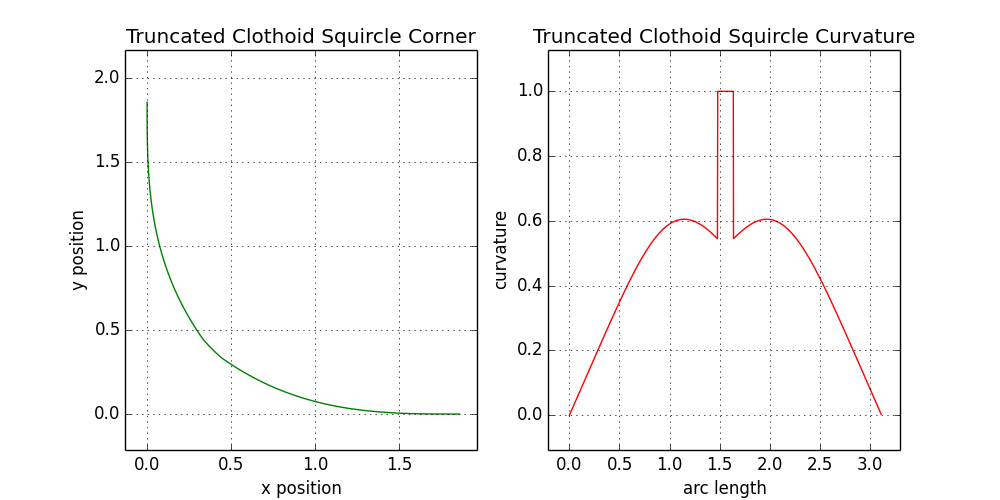
9.3. Угол квадрокруга при ξ = 0,9 с использованием клотоид третьего порядка и дуг окружностей
Эта форма явно непригодна для использования. Кажется, трёх порядков недостаточно, чтобы заставить нарастать кривизну по всей длине подъёма и спуска. Это значит, что у нас накапливается огромная ошибка к моменту, когда мы выходим на дугу окружности (средний сегмент). К сожалению, это означает, что наши результаты с клотоидами непригодны для использования. Придётся начинать всё сначала.
Ничто не вечно
Сделаем шаг назад, снова рассмотрим наши ограничения — и попытаемся извлечь всю пользу из предыдущих усилий, прежде чем отправиться в новом направлении.
Во-первых, мы знаем, что у идеальной клотоидной конструкции именно тот профиль кривизны, который нам нужен, но центр кривизны центральной круговой секции меняет своё местоположение как функция от параметра сглаживания ξ. Это нежелательно, потому что в UI для cкругления прямоугольника указана точка прямо в центре кривизны. Пользователь устанавливает радиус угла, перетаскивая её. Будет немного странно, если эта точка начнёт перемещаться по мере изменения сглаживания. Кроме того, в форме iOS центральная секция находится там, где была бы в случае простого скруглённого прямоугольника, что ещё раз указывает на полную независимость местоположения центра от ξ. Таким образом, мы можем сохранить ту же основную цель проектирования кривизны и добавить ограничение, что круговая секция сохраняет фиксированный центр кривизны при изменении ξ.
Во-вторых, мы знаем, что дизайнерам не нужен слишком сложный инструмент создания углов квадрокруга. В фигуре Apple (после удаления странной крошечной прямой части) только одна кривая Безье, соединяющая круговую секцию с входящий частью кривой — может, и мы так сделаем?
В-третьих, у нас немного непонятные технические ограничения. Они не очевидны с самого начала, но становятся серьёзной проблемой реализации. Чтобы понять их, рассмотрим квадрат 100×100 пикселей, со стандартным скруглением для радиуса угла 20px. Это значит что на каждой стороне квадрата остаётся по 60px прямого отрезка. Если мы сплющим квадрат в прямоугольник 80×100px, то прямой участок короткой стороны будет только 40px. Что происходит, когда мы сужаем прямоугольник так сильно, что у нас заканчивается прямой фрагмент? Или если продолжаем его сужать дальше в прямоугольник, скажем, 20×100px? В данный момент Figma определяет максимально применимое значение скругления углов — и использует его. Таким образом, в прямоугольнике 20×100px будет скругление с радиусом 10px.
Если для сглаживания углов с радиусом R и параметром ξ задействуется p пикселей, то функция p(R,ξ) должна быть обратима в ξ(R,p).
Любой процесс сглаживания в квадрокруге съест ещё больше пикселей прямой стороны, чем простое скругление. Представьте тот же квадрат 100×100px, сделайте скругление 20px, а затем примените некоторую процедуру сглаживания, которая удаляет ещё по 12 пикселей с прямых сторон. Это оставляет нам всего 36px в прямой секции. Что происходит при сужении прямоугольника до 60×100px? По аналогии кажется почти очевидным, что следует уменьшить масштаб сглаживания до такого уровня, чтобы оно не превышало размер прямой секции. Но как вычислить величину ξ, удовлетворяющую определённому количеству пикселей? Вычисление должно быть быстрым, иначе мы не сможем реализовать данную функцию.
Опять же, проблема очень точно описывается математически: если сглаживание углов с радиусом R и параметром ξ потребляет p пикселей, то функция p(R,ξ) должна быть обратима в ξ(R,p). Это несколько скрытое ограничение, которое тоже исключает решение рядом клотоид высокого порядка.
Наконец, у нас есть ограничение юзабилити: изменение сглаживания должно быть хоть как-то заметно на фигуре. Если мы дёргаем параметр сглаживания ξ туда и обратно между нулем и единицей, то хотелось бы видеть разницу! Представьте, что вся наша работа приводит лишь к едва заметным изменениям — это неприемлемо. Таково принципиально требование полезности, и по сути это самое главное ограничение.
Чем проще, тем лучше
Давайте попробуем самый простой подход, какой только можем придумать, при этом соответствующий перечисленным ограничениям. Просто возьмём одну параметризованную кривую Безье, которая берёт круговую часть и связывает её с прямой стороной. На рисунке ниже показан подходящий тип кривой Безье.
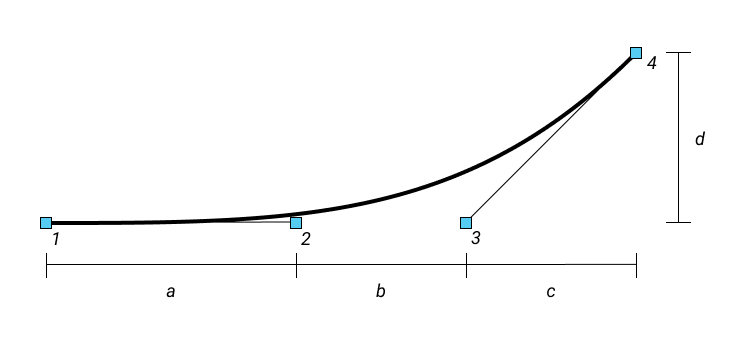
11.1. Контрольные точки кубической кривой Безье для восходящей части угла квадрокруга
Некоторые свойства этой кривой Безье заслуживают дальнейшего объяснения. Во-первых, контрольные точки 1, 2 и 3 выстраиваются в линию. Это гарантирует нулевую кривизну в точке 1, которая соединяется с прямой частью квадрокруга. Вообще, если определить систему координат и связать точку 1 с P1, точку 2 с P2 и т.д., кривизна в точке 1 задаётся следующей формулой:
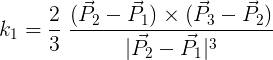
11.2. Неупрощённая кривизна в точке 1 на рис. 11.1
Хорошо видно сокращение дроби, если точки 1-3 выстроены в линию. Ту же формулу применяем к точке 4, указывая координаты в обратном порядке:
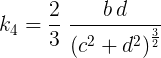
11.3. Упрощённая кривизна в точке 4 на рис. 11.1
В идеале, кривизна получится такой же, как в круговой секции, или 1/R, что приводит к ещё одному ограничению. Наконец, значения c и d зафиксированы из-за того факта, что конец этой кривой должен совпадать с круговой частью и затрагивать места соприкосновения. Значит, вышеуказанное ограничение кривизны просто даёт нам значение b:
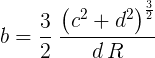
11.4. Решение для b на рис. 11.1, обеспечивающее непрерывность кривизны
Если нам важно сохранить начальное линейное увеличение кривизны (которое является идеальным решением с клотоидами в точке 1), можно установить a равное b, что фиксирует все точки на кривой Безье и даёт нам потенциальное решение. Используя эти наблюдения, мы создаём простой квадрокруг на кривых Безье, используя сглаживание ξ = 0,6.
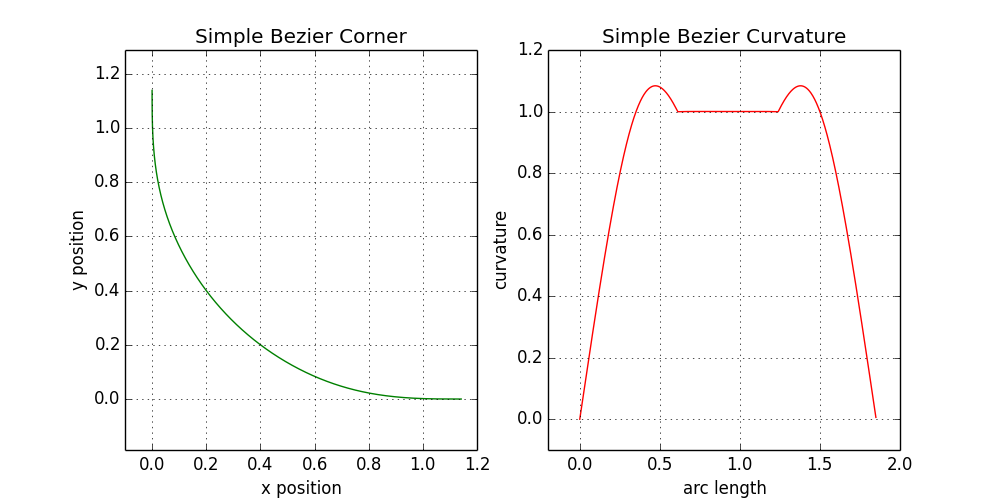
Выглядит неплохо, и здесь используется много подсказок от первоначального расчёта клотоид. К сожалению, разброс по всему диапазону ξ от 0 до 1 практически не заметен на глаз. Ниже показаны углы на двух уровнях масштабирования, с кривыми для ξ = 0,1, 0,3, 0,5, 0,7 и 0,9 разными цветами:
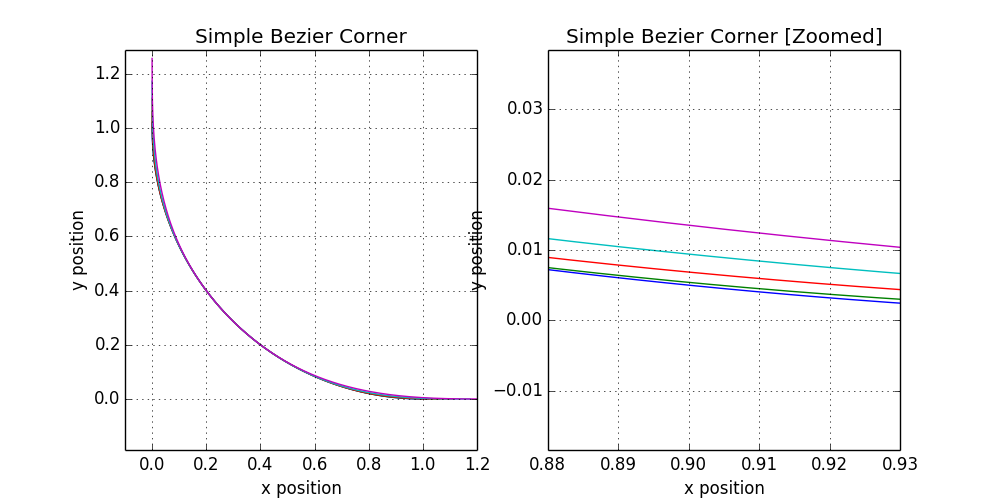
Несмотря на хорошие математические свойства, эффект едва заметен. Конечно, такой вариант ближе к реальному продукту, чем кривая, полученная ранее сокращением ряда клотоид. Если бы только настроить формулу для большей вариативности!
Небольшие штрихи
Можно отойти ещё на шажок и поразмыслить, как действовать дальше. Напомним, нам нужна обратимая связь между пикселями, которые используются при сглаживании, и параметром сглаживания ξ. Сначала можно сосредоточиться на этом преобразовании и сделать его максимально простым. Тогда посмотрим, что получится, когда мы попытаемся сделать из него параметризацию квадрокругов.
Мы уже кое-что знаем о том, как используются пиксели в простом скруглении углов. Не хочу упоминать необходимую тригонометрию, но угол раскрыва θ, скруглённый с радиусом R, задействует q пикселей от вершины угла, причём q задаётся следующим образом:

12.1. Длина сегмента на скругление
Что если мы выберем p(R,ξ) на основе q самым простым способом, например:
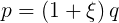
12.2. Длина сегмента на скругление и сглаживание
Это означает, что при максимальном параметре сглаживания будет использоваться та же длина сегмента, которую мы использовали при обычном округлении. Такой выбор зафиксирует количество a + b на рисунке выше. Напомним, что при любых обстоятельствах c и d прочно зафиксированы, поэтому дополнительная фиксация a + b означает, что нам осталось принять одно последнее решение: насколько велико a по отношению к b? Опять же, если сделать самый простой выбор, а именно a = b, то мы закончим с определением параметризации кривой Безье, углы и кривизны которой показаны ниже:
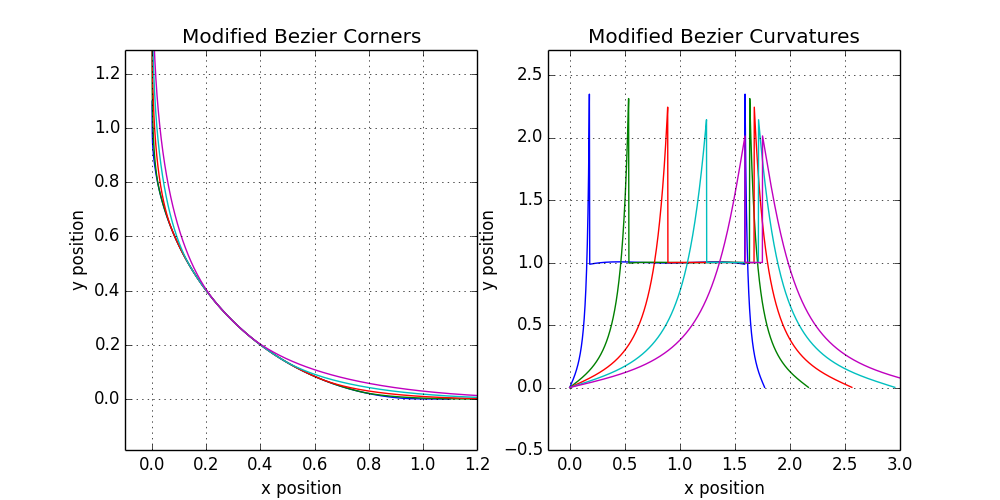
12.3. Форма угла и профиль кривизны для схемы простого сглаживания
Такое визуальное разнообразие уже выглядит многообещающе! Кривые выглядят привлекательно и цельно. Но профиль кривизны грубоват. Вот если бы немного сгладить пики, тогда получится серьёзный кандидат на финальный релиз. Несмотря на слабый профиль, даже в этом простом семействе форм есть экземпляр, очень похожий на версию квадрокруга от Apple. Он почти достаточно хорош, чтобы с чистой совестью выкатить его для наших пользователей.
Теперь перейдём к профилю кривизны, нашей последней нерешённой проблеме. Вместо того, чтобы равномерно разделить разницу между a и b, как мы это делали выше, почему бы не выделить две трети интервала a, а остальное b? Это помешает слишком быстрому увеличению кривизны, уменьшив длинные хвосты на профиле кривизны и обрезав пики. Такое изменение приводит к следующим формам:
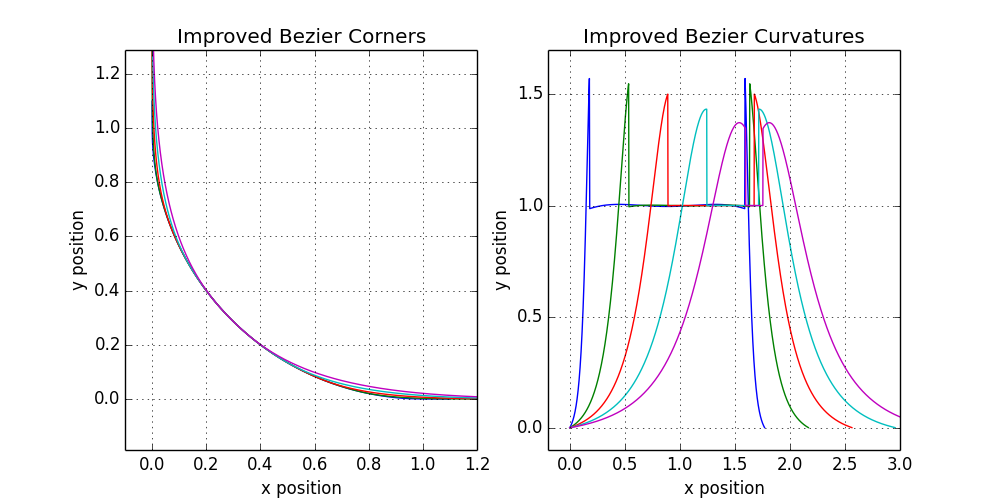
12.4. Форма угла и профиль кривизны для улучшенной схемы простого сглаживания
Профили кривизны значительно улучшились, а визуальное разнообразие по-прежнему достаточно для выпуска реального продукта. Параметр сглаживания ξ = 0,6 почти идеально совпадает с формой iOS, а хороший вид кривых сохраняется несмотря на потрясающую простоту их генерации. Так что пора задать вопрос: что мешает выпустить это в релиз? Ничего.
Размышления после релиза
По итогу полезно поразмыслить над самим процессом. В этой истории неоднократно подтверждалось одно и то же — сила и эффективность простейшего возможного подхода. В худшем случае мы получим базу для сравнения, если он не сработает. Его серьёзная оценка поможет определить самое важное, что следует учесть при доработке подхода и дальнейшем продвижении. А в лучшем случае, как у нас, простейший подход уже даёт достаточно хороший результат!
В конце концов, хочется поразмышлять о разнице между хорошим и совершенным продуктом. Я немного смущён, что не придумал профиль кривизны получше. Уверен, что можно было выделить больше времени, ведь осталось много вариантов для исследования. С интеллектуальной точки зрения немного неприятно, что мы получили такой красивую серию клотоид, но не смогли использовать её в окончательной версии. Но есть и более важный вывод: ограничения времени при работе в небольшой компании очень реальны — а дизайн, который их нарушает, нельзя считать хорошим.
Автор: m1rko






