Из предыдущей части публикации мы узнали, что на одной микросхеме К155ЛА3 можно реализовать достаточно много устройств. Причём у неискушённого читателя мог возникнуть вопрос, зачем же потребовалась разработка других микросхем серии 74, если функциональность любой из них можно реализовать на логических элементах типа 2И-НЕ?
В этой части мы рассмотрим схемотехнические решения на элементах 2И-НЕ более сложных устройств, а также дадим ответ на вопрос неискушённого читателя по результатам анализа работы этих решений.
Полный сумматор
Двоичный сумматор предназначен для формирования на выходе суммы поданных на его входы двоичных сигналов по модулю 2 и сигнала переполнения (переноса).
С формированием результата в виде суммы входных бинарных сигналов по модулю 2 отлично справляется рассмотренная в предыдущей части публикации схема элемента «исключающее ИЛИ». Если дополнить эту схему цепями формирования сигнала переноса, можно превратить её в «полусумматор».
Проще всего это сделать, дополнив схему «исключающего ИЛИ» на четырёх элементах 2И-НЕ ещё одним инвертором, как показано на рисунке ниже:
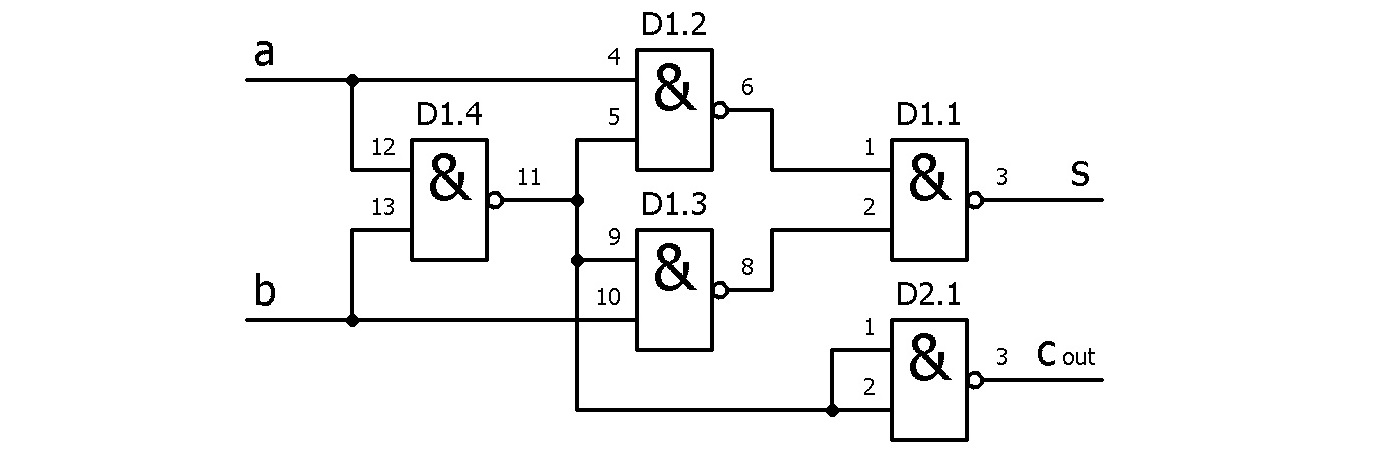
Теперь схема формирует сигнал (флаг) переноса в случае, когда на входы «полусумматора» поданы две логические единицы.
Схему «полусумматора» можно применять только для сложения аргументов разрядностью один бит или младших разрядов многобитных аргументов. Старшие разряды должны суммироваться с учётом значения сигнала переноса при суммировании младших разрядов. Это делает схема «полного сумматора».
На входы схемы «полного сумматора» подаются три двоичных сигнала: два значения суммируемого разряда слагаемых и сигнал переноса, полученный в результате сложения более младших разрядов этих слагаемых. На выходе «полного сумматора» формируется результат сложения этих трёх сигналов, а также сигнал переноса для вычисления суммы более старших разрядов.
«Канонический» вид схемы «полного сумматора» приведён на рисунке ниже:
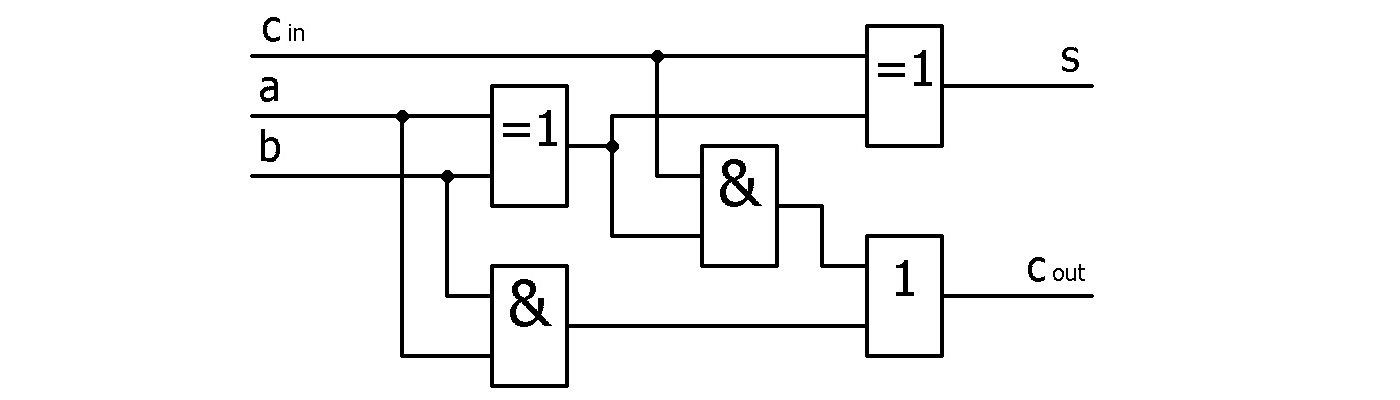
Логические формулы состояния выхода «полного сумматора» и состояния сигнала переноса приведены ниже:
 |
(8) | |
 |
(9) |
Реализовать «полный сумматор» на минимальном количестве элементов 2И-НЕ можно по схеме, приведённой ниже:
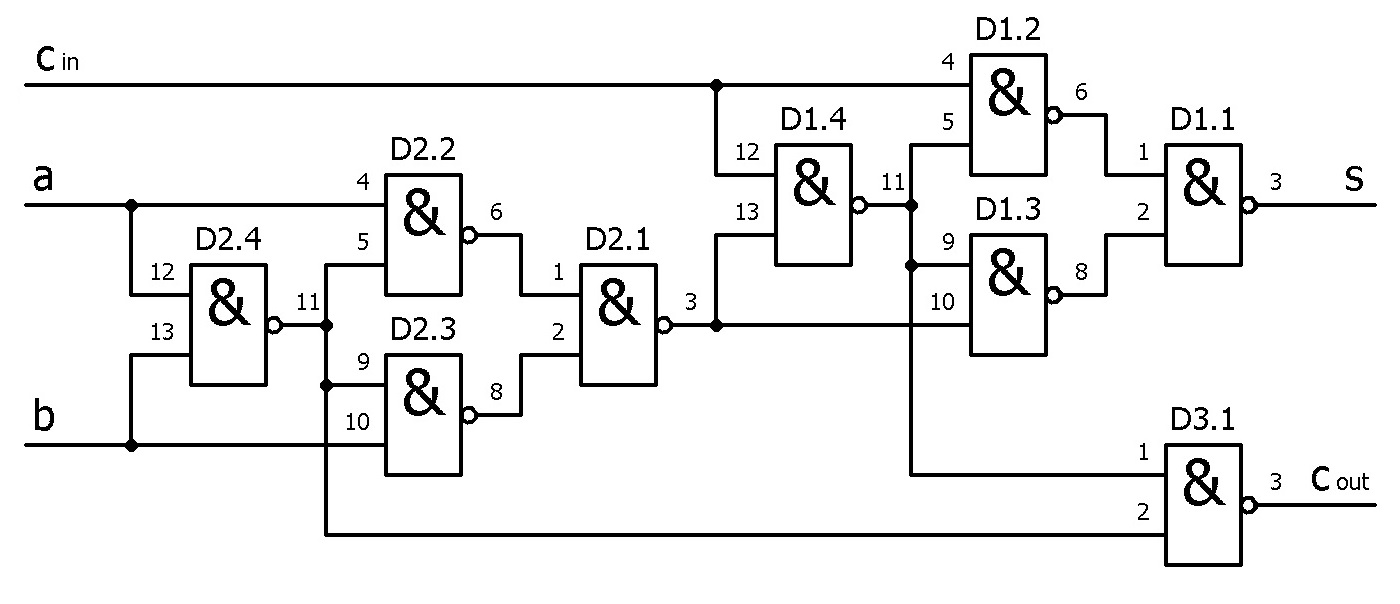
На взгляд неискушённого разработчика цифровой электроники, схема выглядит просто великолепно. Опытный же разработчик, глядя на неё, тут же начнёт рассуждать на тему «гонки состояний».
Задержка распространения сигнала...
В том, чтобы разобраться, что же такое «гонка состояний», нам поможет схема, приведённая ниже:
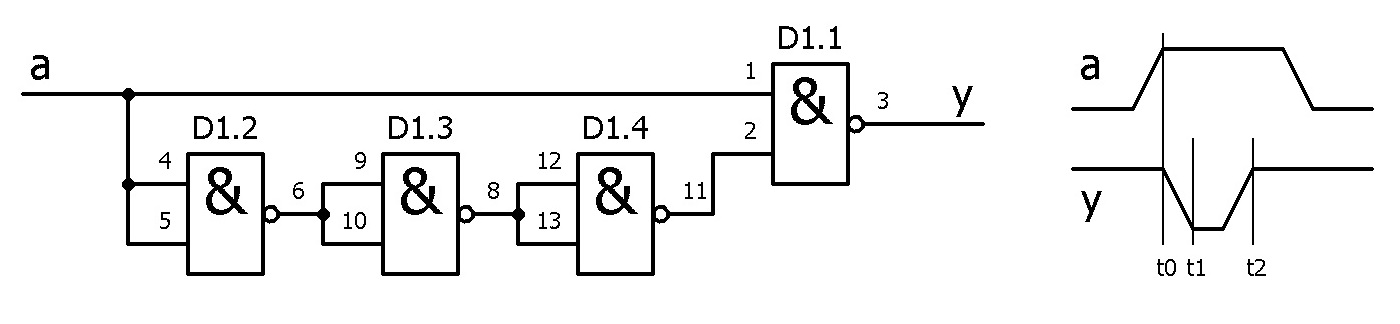
Схема может показаться бессмысленной: казалось бы, какой бы сигнал ни был подан на вход схемы, на её выходе всегда будет сигнал высокого логического уровня, потому что на входах элемента 2И-НЕ, обозначенного как D1.1, всегда будут сигналы разных логических уровней.
Но это – в «статике». В «динамике» же мы попадаем в реальный мир, где фронты логических сигналов никогда не бывают вертикальными, а сигналы распространяются с задержкой.
Рассмотрим временные диаграммы сигналов сбоку от схемы. Изначально на входе схемы и непосредственно на выводе «1» элемента D1.1 присутствует сигнал низкого логического уровня. Цепочка элементов D1.2, D1.3 и D1.4 ведёт себя как инвертор, и на выводе «2» элемента D1.1, присутствует сигнал высокого логического уровня. В результате получаем логическую «единицу» на выходе схемы.
Теперь подадим на вход схемы «единичный» импульс. В момент времени 
начинаются переходные процессы в элементах D1.1 и D1.2, и в момент времени 
на выходе инвертора D1.2 устанавливается сигнал низкого логического уровня. На выходе элемента D1.1 тоже устанавливается сигнал низкого логического уровня, поскольку на выходе инвертора D1.4 всё ещё присутствует логическая «единица».
Если обозначить среднее время задержки распространения сигнала одним логическим элементом как:
 |
(10) |
То сигнал высокого логического уровня на выходе D1.4 появится через ещё 
, а на выходе D1.1 – через три. То есть длительность импульса на выходе схемы будет приблизительно равна 
, что составляет время задержки распространения сигнала цепочки, состоящей из трёх элементов.
Феномен «гонки состояний» заключается в том, работа схемы «в железе» может отличаться от работы математической модели этой схемы. В этом нам помог убедиться пример схемы формирователя импульса по фронту входного сигнала, работу которой мы и разбирали выше.
…имеет свойство накапливаться
Вернёмся к нашему «полному сумматору». Пусть нам нужно найти сумму двух четырёхразрядных чисел. Для этого нам понадобятся четыре подобных сумматора.
Подаём соответствующие разряды слагаемых на соответствующие входы соответствующих сумматоров. Выходы сигналов переноса подаём на входы сигналов переноса следующих разрядов. На вход переноса первого разряда подаём логический «ноль».
Попытаемся оценить время в 
, за которое схема вычислит сумму двух четырёхразрядных чисел.
С первым разрядом всё просто: достоверный сигнал переноса формируется за время, равное 
, достоверное значение суммы – за 
.
Со вторым разрядом немного сложней: достоверное значение суммы без учёта сигнала переноса сформируется за время, равное 
, что справедливо и для третьего и четвёртого разрядов, а вот сигнал переноса для сумматора третьего разряда будет формироваться ещё 
.
Обобщаем: к концу отрезка времени 
будет получено достоверное значение суммы первых разрядов и получено значение сигнала переноса для сложения третьих разрядов; сигнал переноса для сложения четвёртых разрядов будет получен через ещё 
, а достоверное значение суммы двух четырёхразрядных чисел будет получено ещё через три.
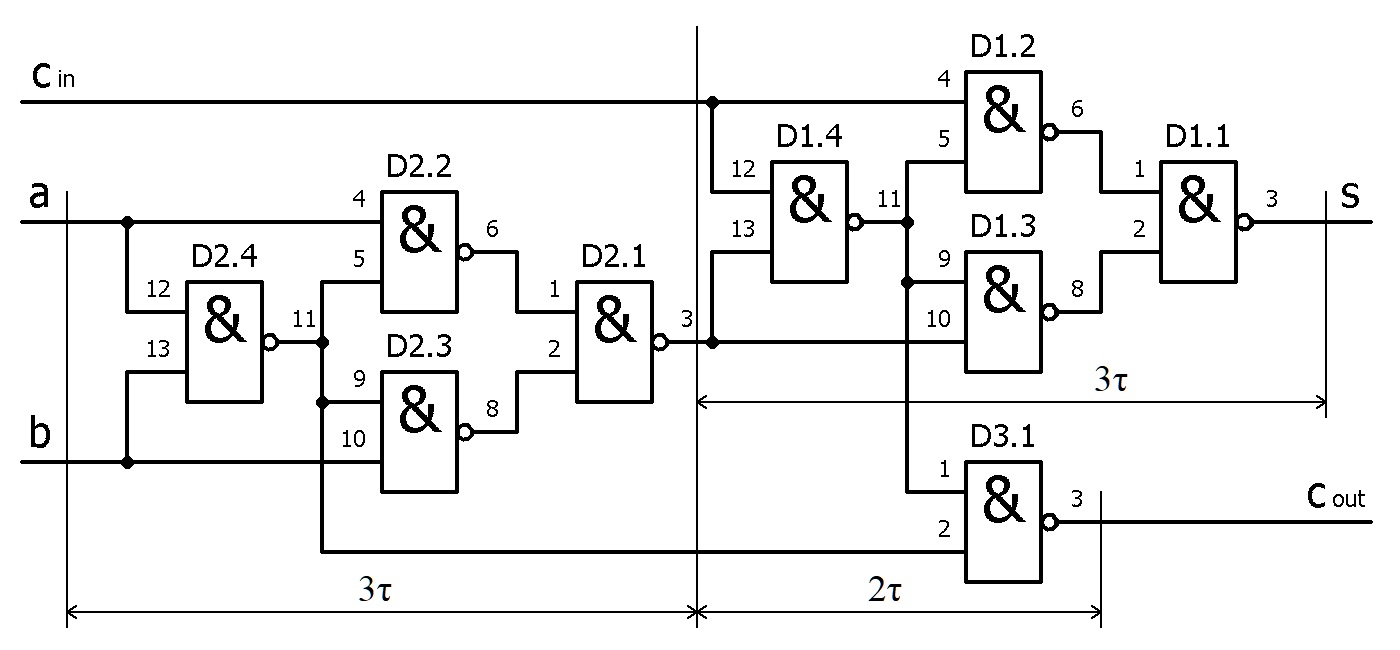
Итого, рассматриваемая схема производит суммирование двух четырёхразрядных чисел за период времени, равный 
, а сигнал переноса в пятый разряд будет получен за 
. При среднем значении времени задержки распространения сигнала для микросхем серии 74 равном 13 нс время суммирования двух четырёхразрядных чисел рассматриваемой схемой четырёхразрядного сумматора на дискретных элементах составит около 130 нс, и всё это время сигналы на выходах нашего четырёхразрядного сумматора будут недостоверны.
Убеждаемся, что для корректной работы рассматриваемого сумматора ей необходимо запоминающее устройство на входе с запретом записи на всё время переходных процессов в схеме, а также запоминающее устройство на выходе с разрешением записи только после окончания переходных процессов. Переходим к триггерам.
Триггер как ячейка памяти...
Самым простым способом реализации ячейки памяти на элементах 2И-НЕ является схема RS-триггера. Устройство имеет два устойчивых состояния, переключение между которыми производится подачей сигналов низкого логического уровня на один из двух входов. При подаче логического «ноля» на вход S (Set) на «прямом» выходе RS-триггера устанавливается сигнал высокого уровня, а при подаче логического «ноля» на вход R (Reset) сигнал высокого логического уровня устанавливается на инверсном выходе триггера и производится сброс «прямого» выхода RS-триггера в «ноль».
С точки зрения применения «классической» схемы RS-триггера в качестве ячейки памяти вычислительных устройств, у неё есть два существенных недостатка: возможность изменения состояния в любой момент времени (асинхронность) и разнесение сигналов управления состоянием по двум разным входам.
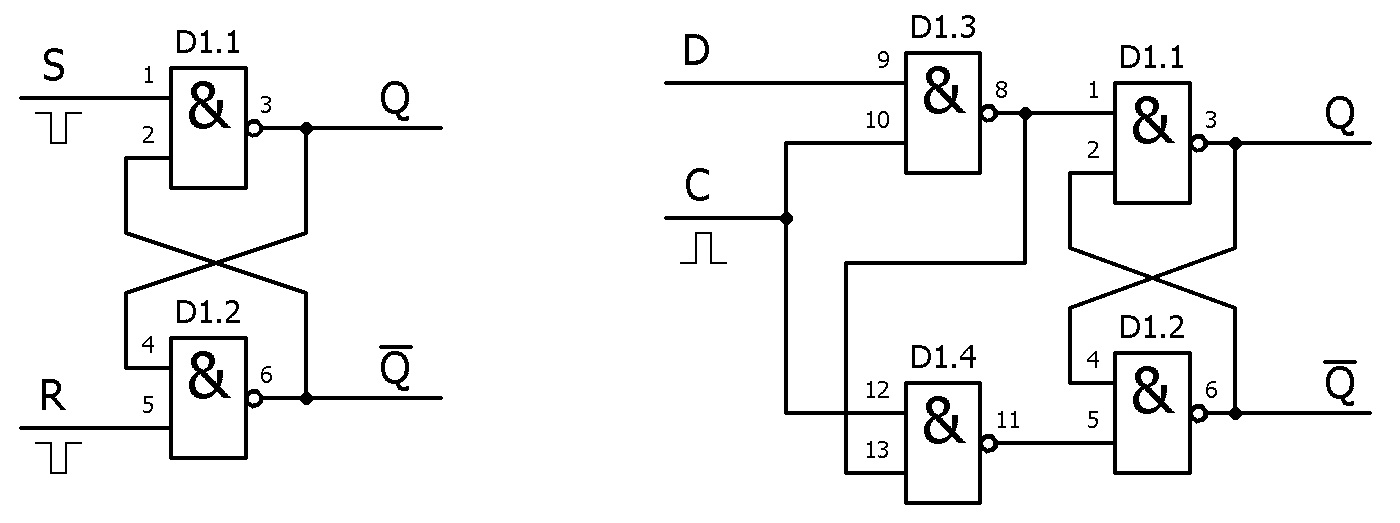
На рисунке выше слева приведена схема RS-триггера на двух элементах 2И-НЕ, а справа – схема «тактируемого» RS-триггера (RST-триггера). Выход RST-триггера устанавливается в «единицу», если на входе S (Set) RS-триггера на элементах D1.1 и D1.2 появится сигнал низкого логического уровня. Он, в своё время, может появиться только при подаче на вход C (Clock) сигнала высокого логического уровня, при условии, что на входе D (Data) присутствует сигнал высокого логического уровня. Если в этот момент времени на входе D установлен логический «ноль», сигнал низкого логического уровня появится на входе R (Reset), что приведёт к «сбросу» триггера.
…должен переключаться по фронту тактирующего сигнала
Казалось бы, оба недостатка устранены, но посмотрим, что произойдёт, если во время, пока на входе C присутствует сигнал высокого логического уровня, сигнал на входе D изменится? А приведёт это к тому, что вместе с этим изменится и сигнал на выходе триггера.
Решений этой проблемы два: триггер, организованный по схеме «ведущий – ведомый»; и триггер, переключаемый по фронту тактового сигнала.
Триггер по схеме «ведущий – ведомый» состоит из двух RST-триггеров со всеми их недостатками. Хитрость заключается в том, что запись в эти триггеры производится по разным фронтам тактирующего сигнала. Когда производится запись в «ведущий» триггер, «ведомый» хранит прошлое состояние и изменение состояния на выходах «ведущего» триггера влияния на него не оказывает. Когда же производится запись в «ведомый» триггер, состояние выходов «ведущего» измениться уже не может.
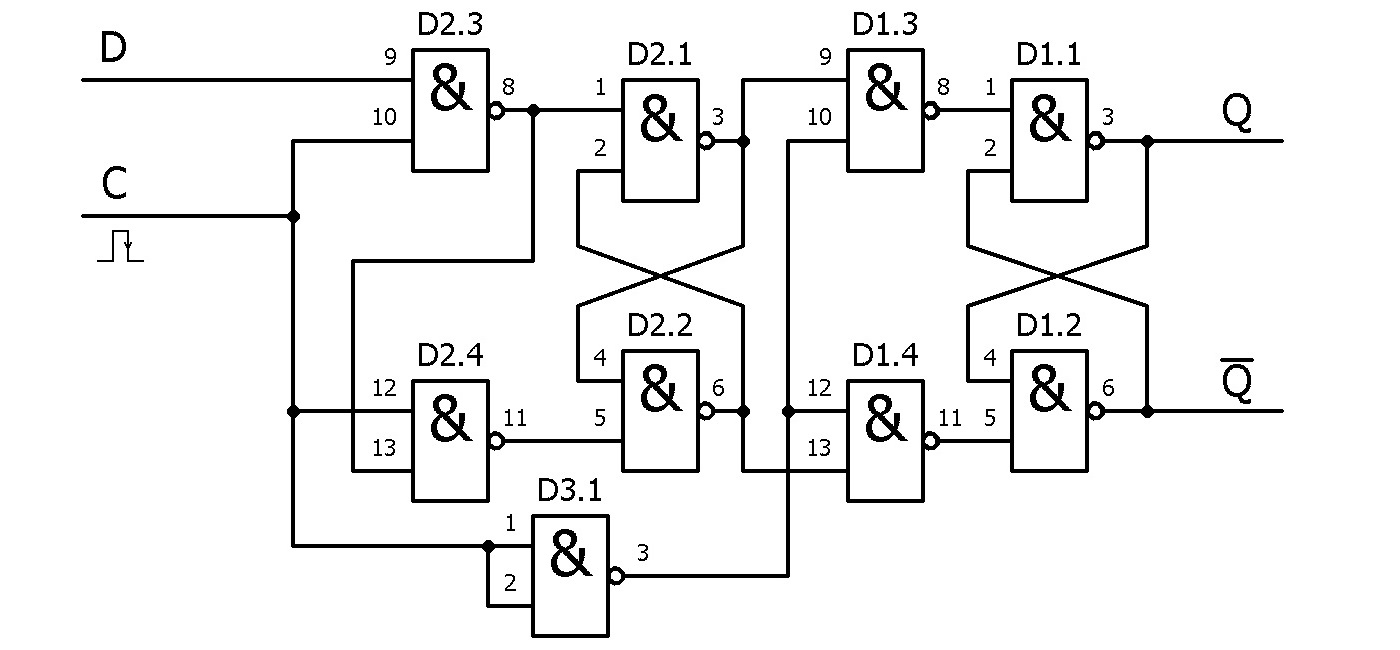
Схема D-триггера, переключаемого по фронту, выглядит не так понятно, но триггеры именно такого типа и получили наибольшее распространение. На рисунке ниже приведена реализация схемы одного из двух триггеров из состава микросхемы К155ТМ2 (7474) только на элементах 2И-НЕ. Для упрощения восприятия из схемы исключены цепи асинхронного сброса и установки.
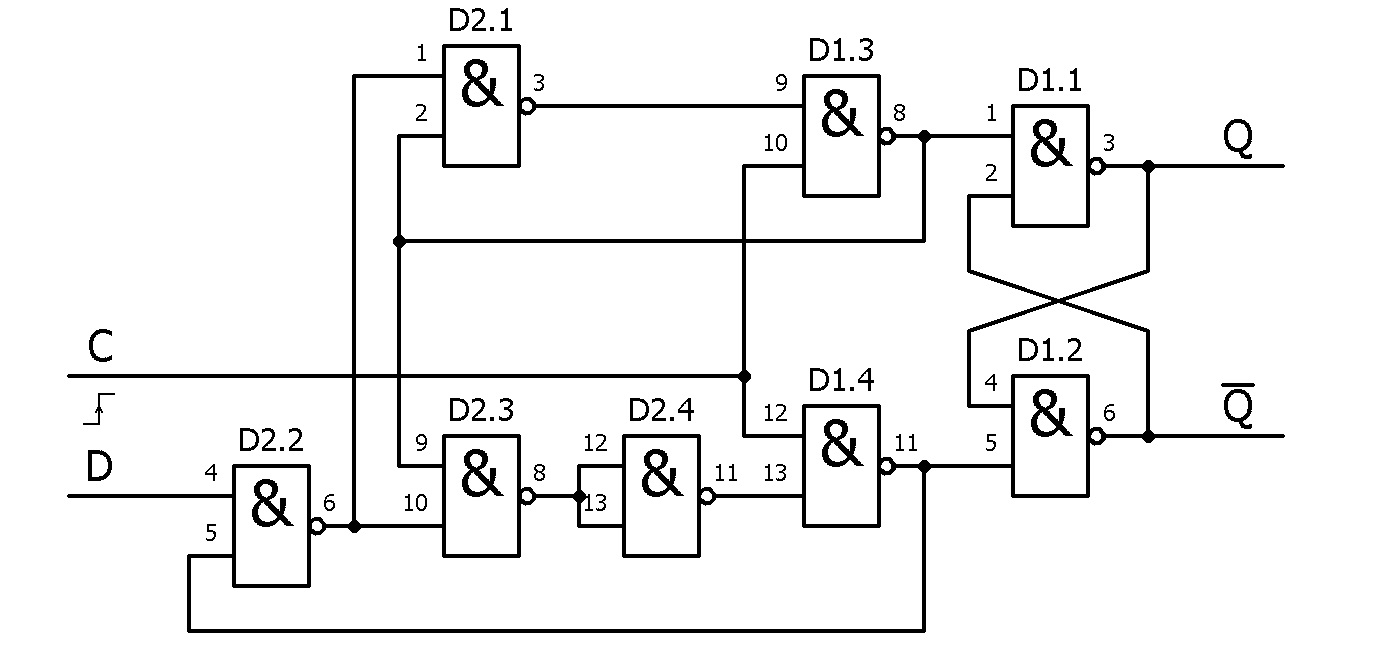
До прихода «переднего» фронта тактового сигнала на входах RS-триггера на элементах D1.1 и D1.2 присутствует сигнал высокого логического уровня. В момент прихода фронта на входах RS-триггера на элементах D1.1 и D1.2 формируется импульс сброса или установки в зависимости от уровня сигнала на входе D. В этот момент времени в триггер записывается его новое состояние, и последующее изменение сигнала на входе D на состояние триггера не влияет до прихода на вход C следующего «переднего» фронта тактового сигнала.
На элементах D2.3, D2.4 и D1.4 реализован элемент 3И-НЕ, о схеме замены которого упоминалось в предыдущей части публикации.
Цветущее разнообразие модельного ряда
Теперь, когда мы убедились в том, что сможем собрать из элементов 2И-НЕ всё что угодно, поговорим про то, почему так обычно не делают.
Вернёмся к четырёхразрядному сумматору на дискретных элементах и посчитаем состав оборудования: пять элементов 2И-НЕ на первый разряд и ещё по девять на три последующих, итого 32 элемента 2И-НЕ (восемь корпусов К155ЛА3) на сумматор. Чтобы запомнить слагаемые на входе, используем восемь D-триггеров на восьми элементах 2И-НЕ каждый (64 элемента, 16 корпусов). Чтобы записать полученную сумму, нужно ещё четыре D-триггера (32 элементов, 8 корпусов). В итоге нам понадобится 32 микросхемы К155ЛА3.
Теперь возьмём за основу готовый четырёхразрядный сумматор К155ИМ3 (7483), а для хранения данных будем использовать три счетверённых D-триггера К155ТМ8 (74175).
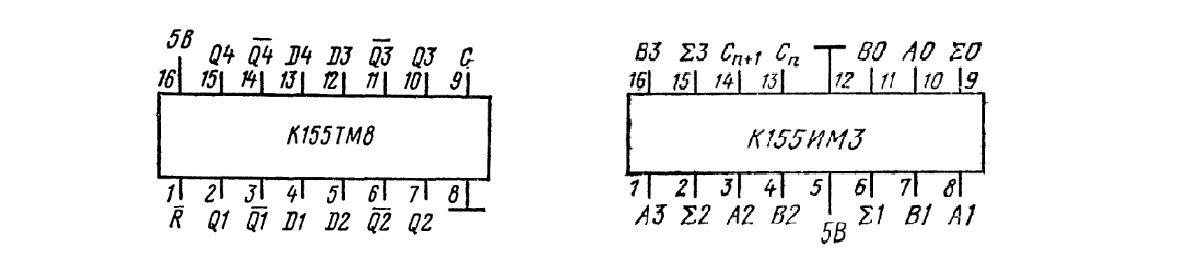
Функциональность схемы осталась той же, но четыре корпуса займут на печатной плате гораздо меньше места, чем 32. Приятным дополнением к уменьшению размеров платы послужит ещё и то, что задержка распространения сигнала по цепи суммы микросхемы К155ИМ3 составляет не более 37,5 нс, а по цепи переноса – не более 40 нс. А это в три с небольшим раза быстрее (130 нс / 40 нс) схемы четырёхразрядного сумматора на дискретных элементах.
От автора
Надеюсь, что две первые части публикации освежили в памяти читателей основы разработки цифровых устройств электроники.
Также надеюсь, что мне удалось убедить читателей, что в разработке техники всегда есть несколько путей решения задач.
Проектирование изделия на ограниченном по номенклатуре модельном ряде «типовых» элементов может упростить процесс закупки комплектующих, но при этом увеличить время разработки. Использование же «специализированных» микросхем может уменьшить габариты, энергопотребление и быстродействие, и при этом не повысить себестоимость, но зато усложнить, допустим, логистику. Любой вариант решения в чём-то неидеален, поэтому выбор варианта решения и производится на основе технико-экономического обоснования.
В следующей, заключительной, части публикации речь пойдёт об аналоговом режиме работы элементов микросхемы К155ЛА3.
▍ Использованные источники:
- Гутников. Интегральная электроника в измерительных устройствах. Энергоатомиздат, 1988.
- Шило. Популярные цифровые микросхемы. 2-изд. Радио и связь, 1989.
- Хоровиц, Хилл. Искусство схемотехники. 2-изд. Мир, 1993.
Автор: Дмитрий Руднев
