Что может быть хуже круговой диаграммы?
Две круговые диаграммы! Эдвард Тафти
Все мы уже не раз видели, что может пойти не так с визуализацией данных. Сегодня обсудим несколько важных принципов, лежащих в основе качественной графики, и что гораздо интересней, узнаем, что произойдет, если эти правила НЕ соблюдать.
Структура статьи
- Восприятие измерений
- Соотношение чернила-данные
- Фактор обмана
- Парадокс Симпсона
- Джон Сноу всё-таки что-то знает — пример классики визуализации
- Что еще посмотреть-почитать
- Круговая диаграмма в реальной жизни
(*осторожно трафик*)
Восприятие измерений
Чаще всего нам необходимо изображать линейные величины на графике т.е. зависимость одной переменной Х, например время в часах, от второй Y, например пройденный путь в км. Пусть 1 см на графике равен 1 часу по Х и 5 км по Y. Вася едет на велосипеде 10 км в час и ехал в течение 4 часов. Значит, изменение по Х составит 4 см, а по Y 40/5=8 см.
Что в подобной ситуации может пойти не так?
Площадь и трехмерные эффекты
Вся хитрость в деталях: представим, что некоторой реальной измеряемой величине X1 соответствует точка Y1 на графике, а X2 точка Y2, а значит, что при изменении данных от X1 до X2 разница на графике составит Y2 — Y1. Но не тут-то было — на круговой диаграмме это будет соответствовать разнице площадей, а если добавить трехмерные эффекты, то и объемов.
Примеры в студию! Представим, что доля Андроида выросла на несколько процентов. Тогда на графике ниже доля вырастет пропорционально объему, а не линейной шкале. Чем это грозит? Прежде всего, это ведет к абсолютному непониманию читателем рассматриваемых величин и невозможности корректного сравнения величин. Кто сможет угадать какая доля у Blackberry на этом графике и насколько она меньше доли iPhone?

Восприятие объема
Спасут ли ситуацию явно прописанные на графике величины? На самом деле нет. Рассмотрим простой пример, где все величины явно прописаны. На графике ниже зеленая часть явно в два раза больше желтой, но на самом деле это не так.

(кликабельно; взято отсюда)
Тортиковая вечеринка
Вот тут внимательный читатель может заявить, что мы рассматривали исключительно патологические примеры с трехмерными эффектами и если использовать стандартные круговые диаграммы, то всё пройдет как по маслу. Внимание вопрос, насколько точно можно сравнить данные между категориями по данному графику?
Соотношение чернила-данные
Теперь перейдем от вопроса восприятия данных на графике к информативности. Вопрос: какое количество информации передает этот график?

Ответ: 4(!) числа, причем коричневая часть зрительно выглядит заметно меньше зеленой из-за трехмерной перспективы.
Можем ли мы улучшить данную круговую диаграмму? Для этого зададим несколько важных вопросов:
- Действительно ли здесь нужен цвет? Если да, то какую функцию он выполняет?
- Какую функциональную роль играет здесь трехмерный эффект?
- Легко ли можно сравнивать числа между собой, стоит ли изменить тип графика?
- Облегчает ли фон чтение и восприятие графика?
- Не дублируют ли функциональные элементы друг друга, например текстовые метки и использование цвета?
Если мы ответим на эти вопросы, то можем получить что-то схожее с вот таким графиком:

Минималистичный пример, не отвлекающий читателя от главного.
На данную тему всячески рекомендую курс на Udacity: Data Visualization and D3.js
В частности по этому вопросу, у них есть отличное видео:
После просмотра видео сравните эту визуализацию
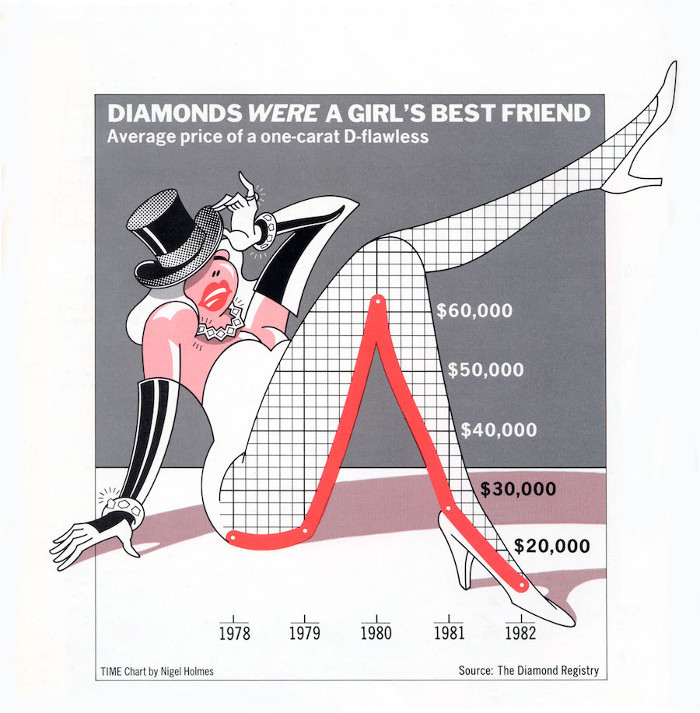
и эту
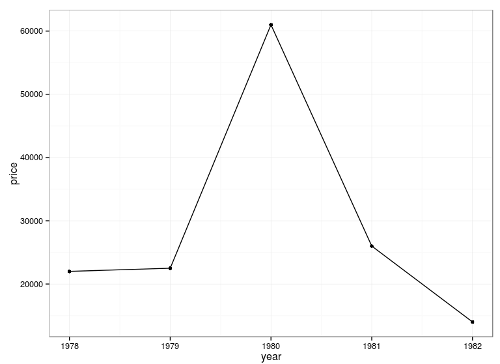
(хотя некоторые с этим примером в качестве «неправильной визуализации» не согласны, и дебаты не скончаются по сей день).
Фактор обмана
Если графики с площадями и объемами не убедили, то настала пора написать убедительную формулу.
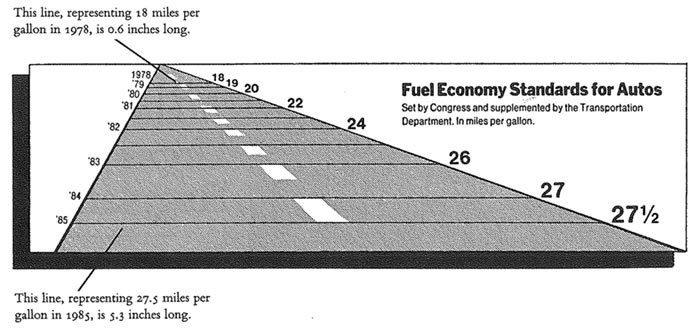
На графике выше количество миль на галлон топлива изменилось c 18 до 27.5, то есть на 53%, рост на графике составил 783%, теперь давайте рассчитаем фактор обмана.

Подставив числа, получим 783/53 = 14.8, мы преувеличили рост с помощью графики практически в 15(!) раз.
Подробнее и примерами можно прочитать тут.
Упражнение со звёздочкой: посчитать фактор обмана с учетом того, график показывает объем вместо линейных размеров. Мне кажется или здесь действительно 11 невероятно больше 9, а 6 и 11 вообще не сравнимы?
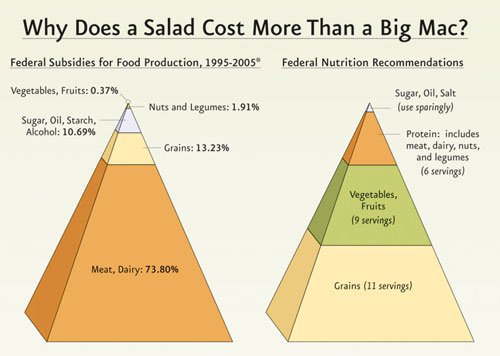
(Взято отсюда)
Парадокс Симпсона
Подвох может находиться и там, где его меньше всего ждут. Визуализируя данные, мы часто разбиваем их на категории или группы и один из классических сюрпризов, который при этом может возникнуть и называется парадоксом Симпсона.
Рассмотрим в качестве примера Гомера, который решил поправить своё здоровье и начал бегать по стадиону и записывать результаты тренировки по месяцам. Первые четыре месяца он стабильно наращивал на нагрузку, но на пятый месяц нашел коробку с пончиками и прекратил тренировки. Через два месяца совесть и лишний вес снова подтолкнули его начать тренировки и вновь каждый месяц он наращивал нагрузку.
Получается, и в первый период, и во второй нагрузка росла, а в среднем нагрузка стабильно падала.
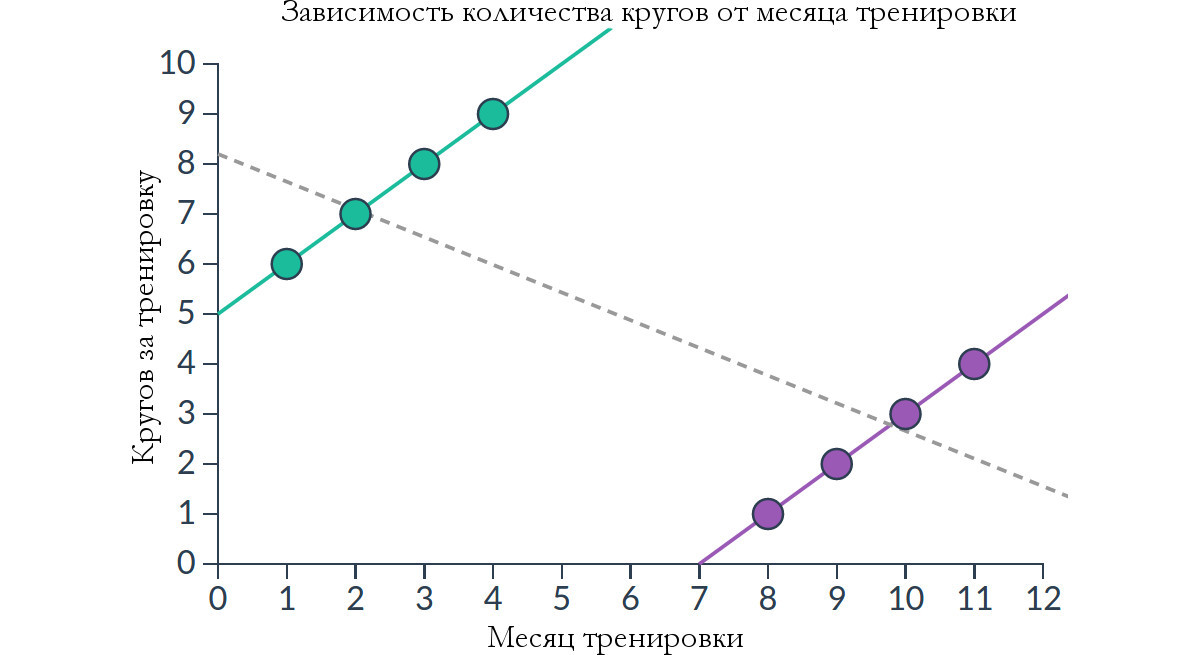
Парадокс заключается в том, что разбив данные на группы, можно обратить негативный тренд в положительный и наоборот.
Графики и примеры вместе с детальным объяснением парадокса можно также найти здесь (рекомендую).
Джон Сноу всё-таки что-то знает — пример классики визуализации
Джон Сноу не только охранял Стену, но и спас жителей Лондона от холеры, используя визуализацию. Он нанес каждого погибшего на карту и заметил, что вокруг водяной колонки на Broad Stree кластер смертей. Тогда-то он и выдвинул гипотезу о том, что источник холеры в зараженной воде колонки. И оказался прав.
Одним из интересных выводов стало то, что пивоварня была самым безопасным местом (ноль смертей), использованная вода и сам процесс приготовления делали пиво гораздо более безопасным к употреблению, чем обычную воду из колонки (правда только в середине 19го века в Лондоне).
Подробная история с интерактивной картой здесь.
Что еще посмотреть-почитать
Видео о росте роли визуализации в политической жизни.

(видео перекинет на другую страницу; можно также кликнуть сюда)
Полезные книги (must read, сейчас наслаждаюсь прочтением первой)
- The Visual Display of Quantitative Information by Edward Tufte
- Functional Art by Alberto Cairo
- The Grammar of Graphics by Leland Wilkinson
Real life pie chart
<юмор> Круговая диаграмма в реальной жизни </юмор>

С пятницей!
Автор: varagian








