Есть битовая матрица, содержащая изображение круга, квадрата или треугольника (фигуры закрашены). Изображение может быть немного искажено или содержать помехи. Задача – написать алгоритм, который по матрице выяснит, какая фигура нарисована на изображении.

Эта простая с первого взгляда задача встретилась мне на вступительном экзамене в DMLabs. На первом занятии мы обсудили решение, а преподаватель (Александр Шлемов; он также руководил дальнейшей реализацией) показал, почему для решения лучше использовать машинное обучение.
В процессе дискуссии мы обнаружили, что наши решения делятся на два этапа: фильтрацию помех и вычисление какой-то метрики, по которой будет проходить классификация. Тут возникает проблема нахождения границ: необходимо знать, какие значения метрики могут получаться для каждой из фигур. Можно проложить эти границы вручную “на глазок”, но лучше поручить это дело математически обоснованному алгоритму. Таким образом мы подходим к использованию методов машинного обучения (Machine Learning).
Таким образом эта учебная задачка стала для меня введением в Machine Learning, и я хотел бы поделиться с вами этим опытом.
Основная идея
Можно придумать несколько метрик, у которых будут разные «плохие случаи» — когда на картинке нарисована одна фигура, а метрика указывает на другую или дает значение, близкое к граничному. Тогда при возникновении такого случая у одной остальные её поправят.
Проблему с границами мы решим с помощью дерева решений (Decision tree), а точнее, с помощью её разновидности: CART (подробнее можно прочитать тут) — она проста и лучше интерпретируется в терминах границ. Это дерево в каждом узле делит данные на подгруппы так, чтобы в результате максимально уменьшить неоднородность в подгруппах (критерий Гини), и повторяет это рекурсивно для каждой подгруппы.
Суть нашего метода: мы создаем много случайных изображений кругов, треугольников и четырехугольников. После этого мы пропускаем каждое через набор фильтров, и вычисляем метрики. На основе этой статистики мы сможем провести границы, что делает дерево решений.
После этого, получив неизвестное изображение, пропустив его через фильтры и вычислив метрики, с помощью этого дерева мы сможем сказать, к какому классу оно относится.
Генерация
Генератор должен не только создавать картинки, а также уметь накладывать на них помехи. При генерации мы должны отбрасывать фигуры с сторонами меньше некой величины (например, 15 пикселей) и с тупыми углами (больше 150 градусов) — даже человеку сложно их классифицировать.
Скрипт заботливо предоставил Виктор Евстратов.
bitbucket.org/rampeer/image-classifier/src/HEAD/picture_generator.py
Фильтры
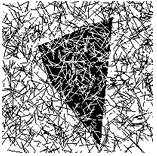
В процессе дискуссии с коллегами мы нашли хорошие идеи для фильтров. Первая — что мы можем определить помехи как пиксели черного цвета, окруженные пикселями противоположного цвета. Эта идея легла в основу медианного фильтра. Вторая — что мы можем определить искомый контур как большое скопление черных пикселей. Это — идея бикомпонентного фильтра.
Медианный фильтр: для каждого черного пикселя мы узнаем количество его «черных» соседей в окрестности с радиусом R. Если это число меньше некого T, то мы отбрасываем этот пиксель, то есть закрашиваем в белый цвет (в «оригинальном» медианном фильтре мы отбрасываем пиксель если у него меньше половины черных соседей, а у нас — порог T, так что на самом деле это квантильный фильтр, но сути это не меняет)

Я написал медианный фильтр честно и «в лоб». При таком написании он будет работать за O(WHR2), где W и H – размеры картинки. Преподаватель сообщил, что это можно сделать быстрее, использовав преобразование Фурье. И вправду, медианный фильтр можно выразить через свертку. А свертку можно вычислить быстро с помощью быстрого преобразования Фурье. Таким образом, у нас получается, что вычислить матрицу с количеством соседей можно как
result = FFT-1 (FFT(data) FFT(window)).
Это работает за O(WHlog(W+H)), не зависит от размеров окна, и в нашем случае работает немного быстрее наивной реализации. Из-за цикличности свертки возникает артефакт на границах: при обработки крайних левых пикселей: их соседями будут считаться крайние правые. Это можно победить, добавив рамку из чистых пикселей по краям изображения. А можно с этим и не бороться, что я и сделал — всё равно этот эффект незначителен и не наносит ущерба работоспособности.
bitbucket.org/rampeer/image-classifier/src/HEAD/filter_median.py
Я обнаружил у этого фильтра нехорошее свойство: он “скругляет” острые углы треугольников. Из-за этого приходится держать радиус окна R довольно маленьким, и проходится по изображению фильтром только несколько (N) раз. Хотя поначалу казалось, что можно применять медианный фильтр до тех пор, пока он удаляет какие-то пиксели, но на практике этот способ не оправдал себя.
Бикомпонентный фильтр: берем произвольный черный пиксель, назначаем ему какое-то число Q. Затем назначаем это же число «черным» соседям этого пикселя в окрестности с радиусом R. Затем повторим этот процесс для соседей соседей. Будем это повторять до тех пор, пока имеются соседи (это напоминает действие инструмента «Заливка» в Paint, а красим в цвет Q). Затем увеличим число Q на единичку, выберем очередной пиксель без назначенного ему числа, и повторим процесс.
После выполнения этого алгоритма у нас получится набор несоприкасающихся островов. Мы можем с высокой достоверностью сказать, что самый большой остров – это и есть фигура, а остальные – помехи.
<filter_bicomp.py>
В отличие от предыдущего, этот фильтр не портит изображение. Он может нанести ущерб только если фигуру пересечет линия из помех шириной больше T, что маловероятно.
Я обнаружил у медианного фильтра ещё одно свойство, в этот раз — положительное. Он разбивает пространство, заполненное помехами, на “островки”. Значит, применив потом бикомпонентный фильтр, мы получим контур с прилепившимися помехами. После обработки бикомпонентным стоит ещё раз пройтись медианным, чтобы убрать оставшиеся неровности. Затем надо построить вокруг оставшихся точек выпуклый контур, заполнить его и вычислять метрики уже для него.
bitbucket.org/rampeer/image-classifier/src/HEAD/process.py
Работа фильтров:
| Исходное изображение | Медианный фильтр | Медианный, бикомпонентный | Медианный, бикомпонентный, медианный, заливка |
 |
 |
 |
 |
Параметры фильтров подбираются исходя из размеров изображений в выборке и их зашумленности. Для хитрого четырехугольника, изображенного выше:
median.filter(img, 2, 6, 1)
bicomp.filter(img, 2)
median.filter(img, 2, 5, 2)
В нашей выборке изображения будут менее зашумлены, и настройки будут более щадящие.
Метрики
В ходе всё той же дискуссии с коллегами мы придумали разные интересные метрики.
Подсчет углов. Самое первое, что приходит, наверное, каждому в голову после прочтения задачи. Но из-за помех могут появиться дополнительные углы, близкие к 0 градусам. Я безуспешно пытался бороться с этим с помощью установления порогов или путем «склейки» почти коллинеарных векторов. Такие методы тяжело настроить, а так как при фильтрации фигурка сглаживается, они всё равно могут давать некорректный результат. Лучше просуммировать квадраты синусов углов, а когда углы больше некого порога T– округлять квадрат вверх до единички. Это дает достаточно хороший результат: острые углы прибавляют к счетчику единичку, а углы, близки к 0, почти ничего не прибавляют. Кстати, мне показалось забавным, что в таком случае у треугольника количество углов может варьироваться от 2,5 до 4.
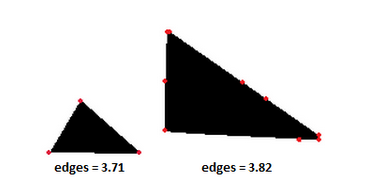
bitbucket.org/rampeer/image-classifier/src/HEAD/feature_edges.py
Зеркалирование. Её смысл – посчитать, насколько фигура будет совпадать сама с собой при отражении по горизонтали/вертикали/вдоль обоих осей. То есть, эта метрика — своеобразная мера симметрии, совпадение изображения с перевернутым. Круг как ни крути – будет всегда полностью совпадать сам с собой. Также, я интуитивно предположил, что квадрат будет больше совпадать сам с собой больше, чем треугольник.

bitbucket.org/rampeer/image-classifier/src/HEAD/feature_mirror.py
Отношение площади к квадрату периметра. Периметр необходимо возводить в квадрат, чтобы метрика не имела размерности и не зависела от размера изображения. Периметр и площадь будем считать от выпуклого контура. Круг имеет набольшее значение метрики среди фигур: s/p^2 =(πr^2)/(4π^2 r^2 )=1/4π. Для равностороннего треугольника (у него это соотношение самое большое среди треугольников): s/p^2 =(4√3 a^2)/(3*9a^2 )=(4√3)/27. Для квадрата: s/p^2 =(a^2)/(16*a^2 )=1/16.

bitbucket.org/rampeer/image-classifier/src/HEAD/feature_perimeter.py
Метрики на описывающем прямоугольнике. Предыдущие метрики не очень хорошо разделяли четырех- и треугольник, и я решил придумать новую метрику. Построим ограничивающий прямоугольник вокруг фигуры. Для каждой стороны прямоугольника найдем первое (“минимальное”) и последнее (“максимальное”) пересечение с фигурой. У нас получится “восьмиугольник”, для которого можно вычислить разные метрики.
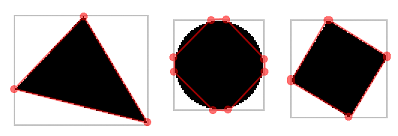
Например, отношение площади фигуры к площади описывающего квадрата (sbound).
bitbucket.org/rampeer/image-classifier/src/HEAD/feature_sbound.py
Также многообещающей метрикой может быть отношение площади фигуры к площади этого восьмиугольника (sbound2):
bitbucket.org/rampeer/image-classifier/src/HEAD/feature_sbound2.py
Сбор данных
Применив полученные знания, я сгенерировал изображения и собрал статистику. В сгенерированные изображения я добавил изображения, представляющие собой потенциальные “плохие случаи” для метрик:
- равносторонний треугольник
- прямоугольный треугольник с двумя сторонами, параллельными осями
- квадрат со сторонами, параллельными осям.
Этим случаям я дал большой вес при построении дерева. Дело в том, что вероятность случайной генерации таких картинок мала, а эти случаи являются граничными для некоторых метрик, и для их корректной классификации надо их добавить в выборку с большим весом.
Процедуру фильтрации изображения и сбора метрик я вынес в отдельный файл – она также понадобится для анализа. Кстати, в дереве решений наши метрики называют “входными параметрами” или “фичами” (feature).
bitbucket.org/rampeer/image-classifier/src/HEAD/process.py
bitbucket.org/rampeer/image-classifier/src/HEAD/stats.py
Затем я построил график, чтобы убедиться, что метрики достаточно хорошо различают фигурки. Для этого подойдет график типа “коробки с усиками”:
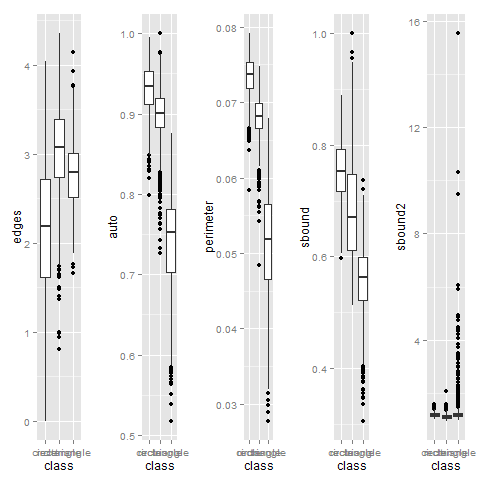
“Усики” пересекаются, а это означает, что возможны неточности при анализе. Как было написано выше, именно для точности нам нужны несколько метрик, а не одна. Дальше я попробовал убедиться, что «плохие случаи» метрик не пересекаются. Для этого я построил зависимость одной метрики от другой. Если получится, что они монотонно зависят друг от друга, то их “плохие случаи” также совпадут.
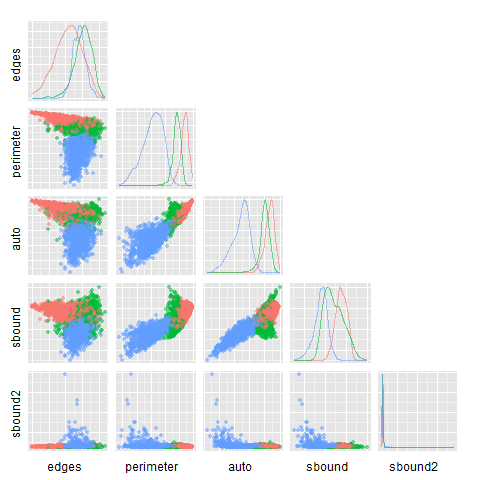
*Как мы видим по графикам, “облака” точек сильно пересекаются. Значит, при классификации возможна большая ошибка. Также, метрики не зависимы монотонно друг от друга.
Анализ
По собранным данным можно построить дерево решений:
bitbucket.org/rampeer/image-classifier/src/HEAD/analyze.py
Я попробовал визуализировать дерево. Получилось вот такая схема:
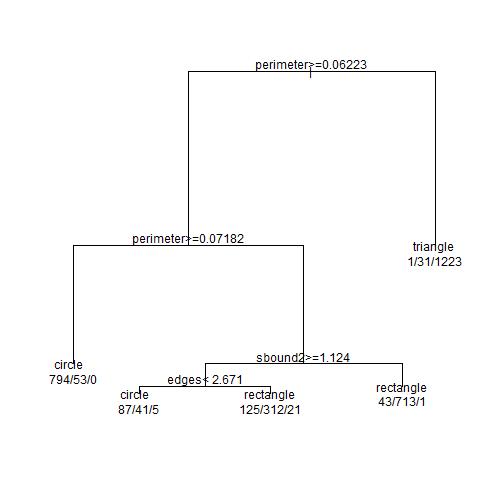
Из неё следует, что некоторые метрики остались не использованными. Мы не могли с самого начала предсказать, какие метрики окажутся “лучше” других.
Точность предсказания составляет примерно 91 процент, что неплохо, учитывая искажения квадратов и помехи в выборке:

Попробуем нарисовать изображения самостоятельно и проанализировать их:
 Circle |
 Rectangle |
 Triangle |
Попробуем повысить напряжение.
Будем искажать фигуры до тех пор, пока они не станут неправильно определяться.
 Rectangle |
 Rectangle |
 Triangle |
 Rectangle |
Вот и всё.
В последнем изображении углы треугольника сильно скруглены, edges не может верно работать, а perimeter дает слишком большую погрешность. Треугольник неудачно повернут: при построении ограничивающего прямоугольника только две вершины будут касаться его, и sbound и sbound2 не выдадут ничего разумного. Только mirror мог бы выдать корректный результат, но он не включен в дерево. Да и если из 5 метрик только одна укажет на треугольник, то её указание можно трактовать как ошибочное.
Вывод
Методы машинного обучения позволили нам построить систему, которая хорошо справляется с поставленной задачей – она достаточно хорошо распознает фигурки на изображении.
Графики были построены в R:
bitbucket.org/rampeer/image-classifier/src/HEAD/charts.R
Автор: dmstudent






