Доброго времени суток. Этот топик рассчитан на тех, кто имеет представление об ограниченных машинах Больцмана (restricted Boltzmann machine, RBM) и их использовании для предобучения нейронных сетей. В нем мы рассмотрим особенности применения ограниченных машин Больцмана для работы с изображениями, взятыми из реального мира, поймем, почему стандартные типы нейронов плохо подходят для этой задачи и как их улучшить, а также немного пораспознаем выражения эмоций на человеческих лицах в качестве эксперимента. Те, кто представления o RBM не имеет, могут его получить, в частности, отсюда:
Реализация Restricted Boltzmann machine на c#,
Предобучение нейронной сети с использованием ограниченной машины Больцмана
Почему все плохо
Ограниченные машины Больцмана изначально были разработаны с использованием стохастических бинарных нейронов, как видимых, так и скрытых. Применение такой модели для работы с бинарными даными совершенно очевидно. Однако подавляющее большинство реальных изображений — не бинарны, а представлены как минимум оттенками серого с целым значением яркости каждого пикселя от 0 до 255. Одно из возможных решений проблемы — изменим значения яркости так, чтобы они лежали в промежутке 0..1 (поделим на 255), и будем считать, что пиксели на самом деле бинарны, а полученные значения представляют вероятность установки каждого конкретного пикселя в единицу. Попробуем использовать этот подход для распознавания рукописных символов (MNIST) и вуаля — все работает и работает чудесно! Почему же все плохо?
А потому, что во множестве реальных изображений интенсивность некоторого пикселя почти всегда почти в точности равна средней интенсивности его соседей. Потому интенсивность должна иметь большую вероятность быть близкой к средней и малую вероятность быть даже немного отдаленной от нее. Сигмоидальная (логистическая) функция не позволяет достичь такого распределения, хотя и работает в отдельных случаях, где это оказывается неважно (например, рукописные символы)[1].
Как сделать, чтобы было хорошо...
Нам нужнен способ представления видимых нейронов, который способен говорить, что интенсивность скорее всего равна, скажем, 0.61, менее вероятно 0.59 или 0.63, и очень-очень маловероятно 0.5 или 0.72. Функция плотности вероятности при этом должна выглядеть примерно так:
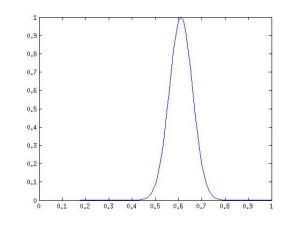
Да это же нормальное распределение! По крайней мере его можно использовать для моделирования такого поведения нейронов, что мы и сделаем, сделав значения видимых нейронов случайными величинами с нормальным распределением вместо распределения Бернулли. Нужно заметить, что нормальное распределение удобно использовать не только для работы с реальными изображениями, но и со многими другими данными, представлеными действительными числами из диапазона [-∞;+∞], для которых не имеет смысла сведение значений к бинарному виду или вероятностям из диапазона [0;1][2]. Скрытые нейроны при этом остаются бинарными и мы получаем так называемую Gaussian-Binary RBM, распределения значений нейронов для которой задаются формулами[3]
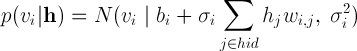
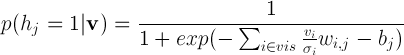
а энергия машины Больцмана равна
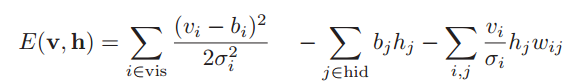
где hid — множество индексов скрытых нейронов,
vis — множество индексов видимых нейронов,
b — bias (смещение),
σi — стандартное отклонение для і-го видимого нейрона,
wi,j — вес связи между i-м и j-м нейроном,
N(x | μ, σ2) — вероятность значения х для переменной с нормальным распределением с матожиданием μ и дисперсией σ2.
Рассмотрим, как изменяется энергия RBM при изменении vi. Компонент bi (bias) отвечает за желаемое значение i-го видимого нейрона (интенсивность соответсвующего пикселя изображения), а сама энергия растет квадратически с отклонением от этого значения:
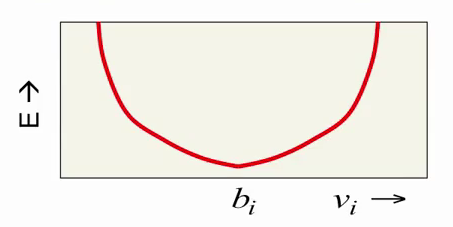
Последний компонент формулы, зависящий как от vi, так и от hi, и представляющий их взаимодействие, зависит от vi линейно:
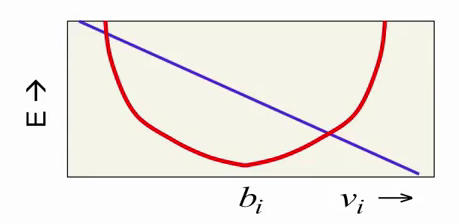
Суммируясь с красной параболой, этот компонент смещает энергетический минимум в ту или другую сторону. Таким образом мы получаем нужное нам поведение: красная парабола пытается ограничить значение нейрона, на давая ему сильно отдаляться от определенного значения, а фиолетовая линия смещает это значение в зависимости от скрытого состояния RBM.
Однако и здесь возникают трудности. Во-первых, для каждого видимого нейрона нужно подобрать в результате обучения подходящий параметр σi. Во-вторых, малые значения σi сами по себе порождают трудности в обучении, обуславливая сильное воздействие видимых нейронов на скрытые и слабое воздействие скрытых нейронов на видимые:
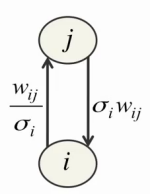
В-третьих, значение видимого нейрона теперь может неограниченно расти, заставляя энергию неограниченно падать, из-за чего обучение становится намного менее стабильным. Для решения первых двух проблем Джеффри Хинтон предлагает нормализовать все тренировочные данные перед началом обучения так, чтобы они имели нулевое матожидание и единичную дисперсию, после чего полагать параметр σi в вышеуказанных уравнениях равным единице[4]. Кроме того, такой подход позволяет использовать точно такие же формулы для сбора статистики и обучения RBM методом CD-n, что и в обычном случае (с использованием только бинарных нейронов). Третья проблема решается простым уменьшением скорости обучения (learning rate) на 1-2 порядка.
… и еще лучше
В результате мы научились хорошо представлять действительные (real-valued) данные видимыми нейронами ограниченной машины Больцмана, однако внутреннее, скрытое состояние все еще бинарно. Можно ли как-то улучшить скрытые нейроны, заставить их нести в себе больше информации? Оказывается можно. Очень легко, оставив скрытые нейроны бинарными, заставить их отображать натуральные числа, большие 1. Для этого возьмем один какой-нибудь скрытый нейрон и создадим множество его копий с точно такими же весами от видимых нейронов (weigth sharing) и обучаемым смещением bi, однако при расчете вероятностей будем отнимать от смещения каждого нейрона фиксированные значения, получив множество в остальном одинаковых нейронов со смещениями bi-0.5, bi-1.5, bi-2.5, bi-3.5… В результате мы получим целочисленную версию rectified linear unit с добавлением шума с дисперсией σ(x) = (1 + exp(-x))-1 (из-за вероятностной природы нейронов). Проще говоря, чем больше будет значение x = bi + ∑vjwi,j на входе такого нейрона, тем больше его копий активируются одновременно, при этом количество всех активированных копий и будет отображаемым натуральным числом:
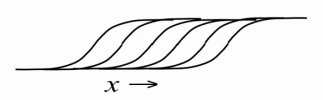
Однако в реальности создавать большое количество копий для каждого нейрона затратно, потому что это в такое же большое количество раз увеличивает количество рассчетов сигмоидальной функции на каждой итерации обучения/работы RBM. Потому поступим кардинально — создадим сразу бесконечное количество копий для каждого нейрона! Теперь мы имеем простое приближение, позволяющее нам считать получающееся значение для каждого нейрона по одной единственной простой формуле[1,5]:
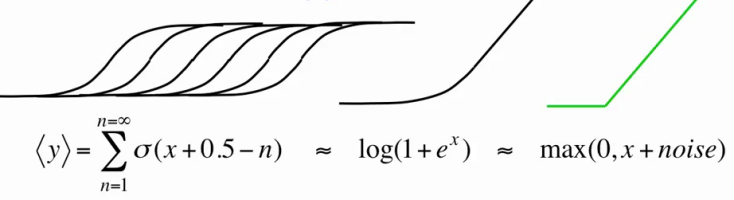
Таким образом наши скрытые нейроны превратились из бинарных в rectified linear units с Гауссовским шумом, при этом алгоритм обучения остался нетронутым (ведь мы предполагаем, что на самом деле это все те же бинарные нейроны, только с бесконечным количеством вышеописанных копий). Теперь они умеют представлять не только 0 и 1, и даже не только натуральные, но все неотрицательные действительные числа! Дисперсия σ(x)∊ [0;1] гарантирует, что полностью неактивные нейроны не будут создавать шума и шум не будет становиться очень большим при увеличении х. Кроме того, приятный бонус: использование таких нейронов позволяет все-таки обучить параметр σi для каждого нейрона, если предварительная нормализация данных по каким-то причинам невозможна или нежелательна[1,2], но на этом подробно останавливаться не будем.
Реализация обучения
Вынося матожидание из формулы нормального распределения, значение видимого нейрона можно считать по формуле
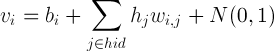
где N(μ, σ2) — случайная величина с нормальным распределением, матожиданием μ и дисперсией σ2.
Джеффри Хинтон в [4,5] предлагает не использовать Гауссовский шум в реконструкциях видимых нейронов при обученни. Аналогично использованию чистых вероятностей в случае бинарных нейронов вместо выбора 0 или 1, это ускоряет обучение за счет уменьшения шума и чуть меньшего времени работы одного шага алгоритма (не нужно считать N(0,1) для каждого нейрона). Последовав совету Хинтона получаем полностью линейные видимые нейроны:
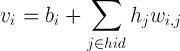
Значение скрытого нейрона считаем по формуле
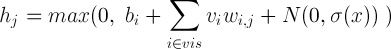
Для реализации самого обучения используем точно такие же формулы, что и для обычных бинарных нейронов в CD-n.
Эксперимент
В качестве эксперимента выберем что-нибудь поинтереснее, чем простое распознавание лиц или рукописных символов. Например, будем распознавать, какая эмоция выражается на лице человека. Используем для обучения и тестирования изображения из баз
Cohn-Kanade AU-Coded Facial Expression Database (CK+),
Yale Face Database,
Indian Face Database,
The Japanese Female Facial Expression (JAFFE) Database.
Изо всех баз выберем только изображения с пометкой конкретной эмоции (одной из восьми: нейтральное выражение, гнев, страх, отвращение, радость, удивление, презрение, грусть). Получим 719 изображений. 70% случайно выбранных изображений (500 штук) используем в качестве тренировочных, а 30% оставшихся (219 штук) — в качестве проверочных (validation data) (в нашем случае они могут использоваться как тестовые, поскольку мы не подбираем с их помощью никакие параметры). Для реализации будем использовать MATLAB 2012b. На каждом изображении выделим лицо с помощью стандартного vision.CascadeObjectDetector, полученную квадратную область расширим вниз на 10% для того, чтобы подбородок полностью входил в обрабатываемое изображение. Полученное изображение лица сожмем до размера 70х64, переведем в оттенки серого и применим к нему гистограмную эквализацию для выравнивания контраста на всех изображениях. После этого каждое изображение развернем в вектор 1х4480 и сохраним соотвествующие вектора в матрицы train_x и val_x. В матрицах train_y и val_y сохраним соотвествующие желаемые вектора-выходы классификатора (размер 1х8, 1 в позиции эмоции, представленной вектором-входом, 0 в остальных позициях). Данные готовы, пора приступать к собственно эксперименту.
Для реализации классификатора выберем существующее решение DeepLearnToolbox, форкнем, допишем нужный нам функционал, исправим баги, недочеты, несоответсвия с гайдом Хинтона и получим новый DeepLearnToolbox, позволяющий просто взять и использовать себя для нашей задачи.
Количества нейронов в каждом слое нашей нейросети: 4480 — 200 — 300 — 500 — 8. Такие маленькие количества нейронов в скрытых слоях выбраны для того, чтобы исключить переобучение (overfitting) и простое запоминание сетью всех входных изображений, так как их количество невелико. Сначала обучим нейросеть с сигмоидальной функцией активации, а для предобучения используем обычные бинарные RBM.
tx = double(train_x)/255;
ty = double(train_y);
vx = double(val_x)/255;
vy = double(val_y);
% train DBN (stack of RBMs)
dbn.sizes = [200 300 500];
opts.numepochs = 100;
opts.batchsize = 25;
opts.momentum = 0.5;
opts.alpha = 0.02;
opts.vis_units = 'sigm'; % Sigmoid visible and hidden units
opts.hid_units = 'sigm';
dbn = dbnsetup(dbn, tx, opts);
dbn = dbntrain(dbn, tx, opts);
% train NN
nn = dbnunfoldtonn(dbn, 8);
nn.activation_function = 'sigm'; % Sigmoid hidden units
nn.learningRate = 0.05;
nn.momentum = 0.5;
nn.output = 'softmax'; % Softmax output to get probabilities
nn.errfun = @nntest; % Error function to use with plotting
% calculates misclassification rate
opts.numepochs = 550;
opts.batchsize = 100;
opts.plot = 1;
opts.plotfun = @nnplotnntest; % Plotting function
nn = nntrain(nn, tx, ty, opts,vx,vy);
График обучения нейросети:
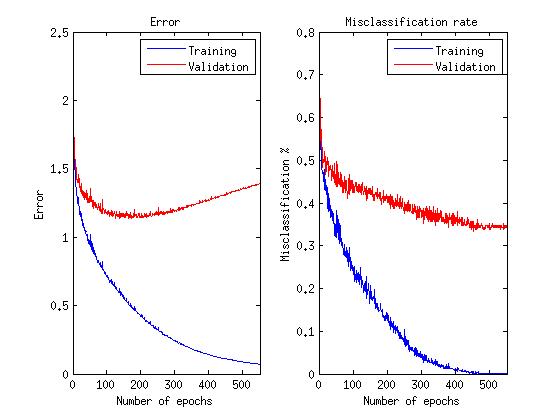
Средняя ошибка на проверочных данных среди 10 запусков с каждый раз новой случайной выборкой тренировочных и проверочных (validation) данных составила 36.26%.
Теперь обучим нейросеть с rectified linear функцией активации, а для предобучения используем описанные нами RBM.
tx = double(train_x)/255;
ty = double(train_y);
normMean = mean(tx);
normStd = std(tx);
vx = double(val_x)/255;
vy = double(val_y);
tx = normalize(tx, normMean, normStd); %normalize data to have mean 0 and variance 1
vx = normalize(vx, normMean, normStd);
% train DBN (stack of RBMs)
dbn.sizes = [200 300 500];
opts.numepochs = 100;
opts.batchsize = 25;
opts.momentum = 0.5;
opts.alpha = 0.0001; % 2 orders of magnitude lower learning rate
opts.vis_units = 'linear'; % Linear visible units
opts.hid_units = 'NReLU'; % Noisy rectified linear hidden units
dbn = dbnsetup(dbn, tx, opts);
dbn = dbntrain(dbn, tx, opts);
% train NN
nn = dbnunfoldtonn(dbn, 8);
nn.activation_function = 'ReLU'; % Rectified linear units
nn.learningRate = 0.05;
nn.momentum = 0.5;
nn.output = 'softmax'; % Softmax output to get probabilities
nn.errfun = @nntest; % Error function to use with plotting
% calculates misclassification rate
opts.numepochs = 50;
opts.batchsize = 100;
opts.plot = 1;
opts.plotfun = @nnplotnntest; % Plotting function
nn = nntrain(nn, tx, ty, opts,vx,vy);
График обучения нейросети:
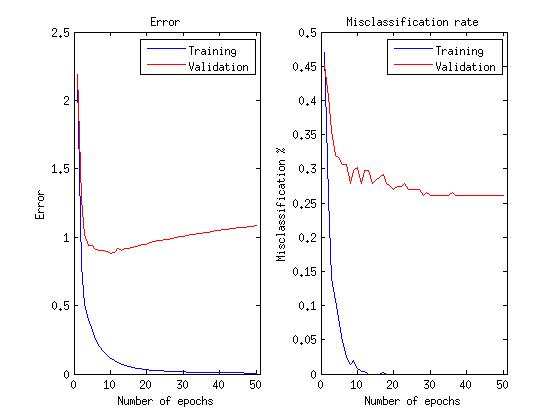
Средняя ошибка на проверочных данных среди 10 запусков с теми же выборками, что и для бинарных нейронов, составила 28.40%
Замечание о графиках: поскольку нас фактически интересует способность сети правильно распознавать эмоции, а не минимизировать функцию ошибки, обучение продолжается, пока эта способность улучшается, даже после того, как функция ошибки начинает расти.
Как видно, использование linear и rectified linear нейронов в ограниченной машине Больцмана позволило уменьшить ошибку распознавания на 8%, не говоря уже о том, что для последующего обучения нейронной сети потребовалось в 10 раз меньше итераций (эпох).
Ссылки
1. Neural Networks for Machine Learning (видеокурс)
2. Learning Natural Image Statistics with Gaussian-Binary Restricted Boltzmann Machines
3. Learning Multiple Layers of Features from Tiny Images
4. A Practical Guide to Training Restricted Boltzmann Machines
5. Rectified Linear Units Improve Restricted Boltzmann Machines
Автор: Igel_SK






