Привет!
Мне показалась интересной данная публикация: Получаем абсолютные курсы из парных кросс-курсов валют и я захотел проверить возможность найти этот аааабсолютный курс валюты через численное моделирование, вообще отказавшись от линейной алгебры.
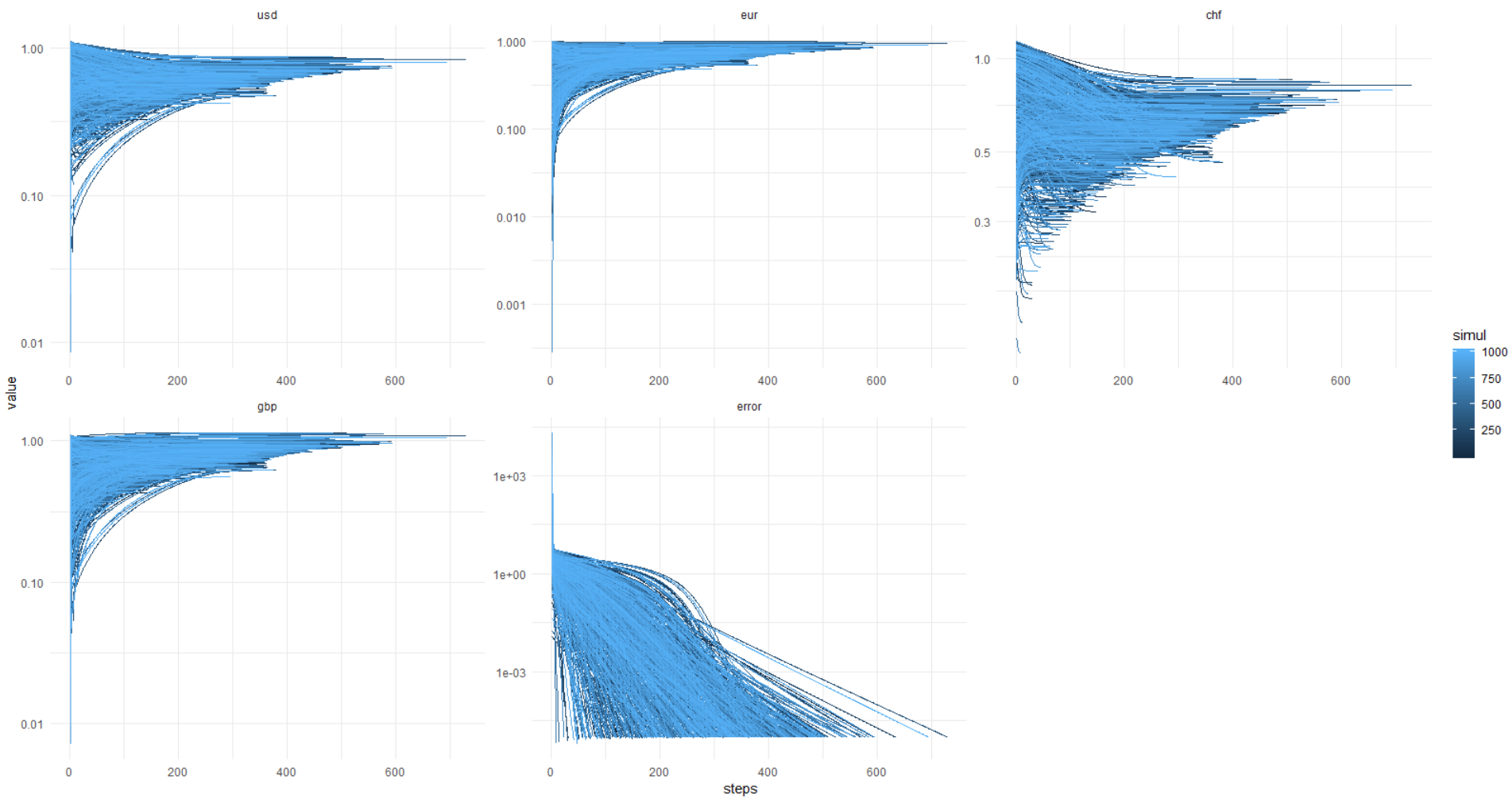
Результаты получились интересными.
Эксперимент будет небольшим: 4 валюты, 6 валютных пар. Для каждой пары одно измерение курса.
Итак, начнем
Гипотеза в том, что стоимость любой валюты можно выразить неким значением, которое будет учитывать стоимости других валют, в которых она котируется, при том, что другие валюты сами будут выражены в стоимости всех других валют. Это интересная рекурсивная задача.
Имеется 4 валюты:
- usd
- eur
- chf
- gbp
Для них был набраны валютные пары:
- eurusd
- gbpusd
- eurchf
- eurgbp
- gbpchf
- usdchf
Обратите внимание, что если число валют n = 4, то число пар k = (n ^2 — n) / 2 = 6. Нет смысла искать usdeur, если котируется eurusd…
В момент времени t был замерен курс валютных пар у одного из провайдеров:
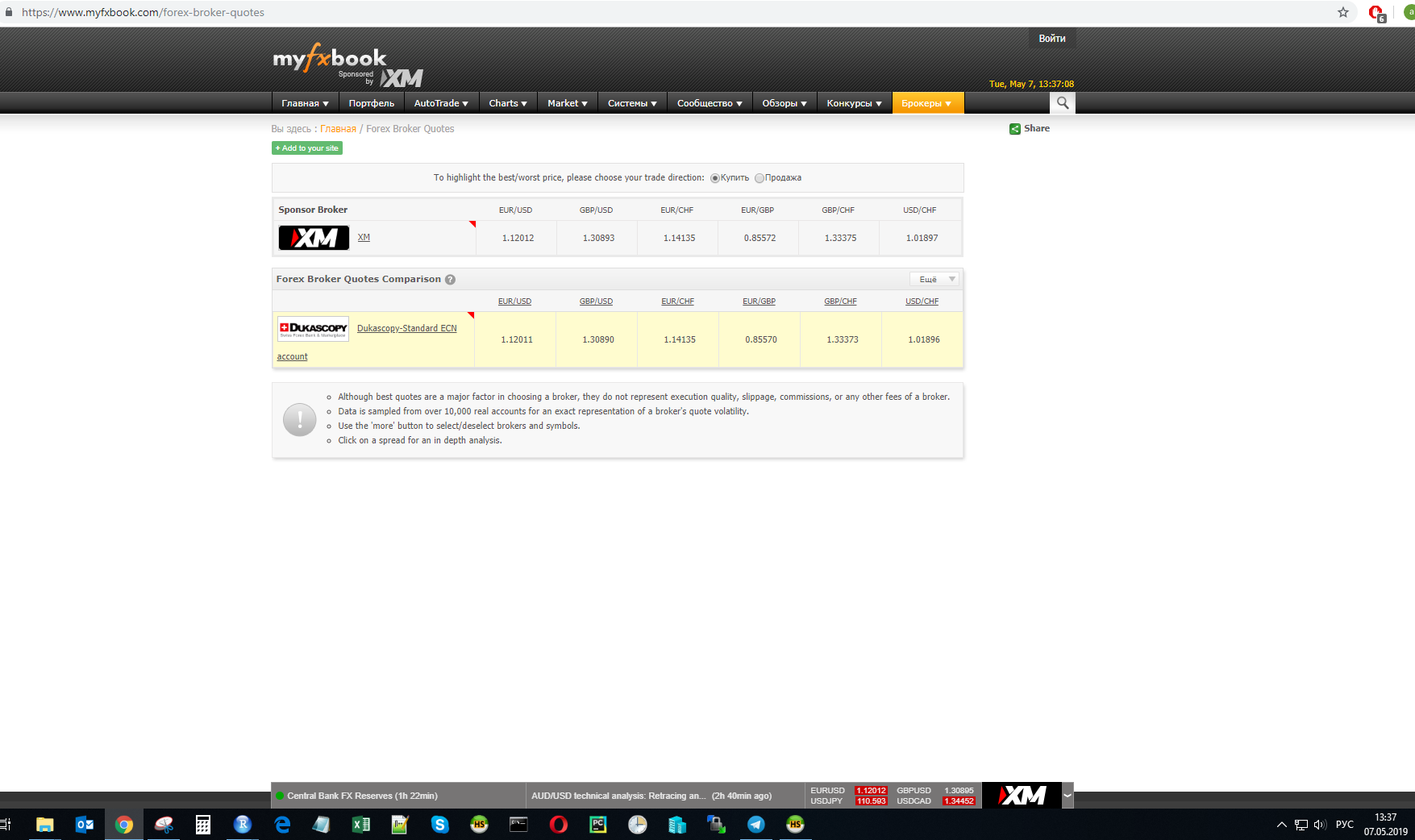
Расчеты будут проводиться для этих значений.
Математика
Я решаю задачку, аналитически беря градиент функции потерь, которая по сути есть система уравнений.
Код эксперимента будет на языке R:
#set.seed(111)
usd <- runif(1)
eur <- runif(1)
chf <- runif(1)
gbp <- runif(1)
# snapshot of values at time t
eurusd <- 1.12012
gbpusd <- 1.30890
eurchf <- 1.14135
eurgbp <- 0.85570
gbpchf <- 1.33373
usdchf <- 1.01896
## symbolic task ------------
express <- expression(
(eurusd - eur / usd) ^ 2 +
(gbpusd - gbp / usd) ^ 2 +
(eurchf - eur / chf) ^ 2 +
(eurgbp - eur / gbp) ^ 2 +
(gbpchf - gbp / chf) ^ 2 +
(usdchf - usd / chf) ^ 2
)
eval(express)
x = 'usd'
D(express, x)
eval(D(express, x))
R позволяет с помощью ф-ии stats::D брать производную функции. Например, если мы хотим продифференцировать по валюте USD, получаем такое выражение:
2 * (eur/usd^2 * (eurusd — eur/usd)) + 2 * (gbp/usd^2 * (gbpusd —
gbp/usd)) — 2 * (1/chf * (usdchf — usd/chf))
Чтобы уменьшить значение функции express, мы будем выполнять градиентный спуск и сразу понятно (видим квадратные разницы), что минимальное значение будет равно нулю, что нам и нужно.
-deriv_vals * lr
Шаг градиентного спуска будет регулироваться параметром lr и все это взято с отрицательным знаком.
То есть, человеческими словами, подберем курсы 4-х валют так, чтобы все валютные пары в эксперименте получили значения равные исходным значениям этих пар. Ммм, решим задачку — в лоб!
Результаты
Чтобы не растягивать, сразу сообщу вам следующее: эксперимент в целом удался, код заработал, ошибка ушла близко-близко к нулю. Но тут я заметил, что результаты всегда получаются разными.
Вопрос знатокам: похоже, эта задача имеет неограниченное количество решений, но в этом я полный ноль, думаю, мне подскажут в комментариях.
Чтобы убедиться в (не)стабильности решения, я провел симуляцию 1000 раз, не зафиксировав сид ГПСЧ для стартовых значений ценности валют.
А здесь идет картинка из ката: error достигает 0,00001 и меньше (так задана оптимизация) всегда, при этом значения валют уплывают черти-знает куда. Получается, всегда разное решение, господа!
Еще раз эта картинка, y-axis в оригинальных единицах (не лог.):
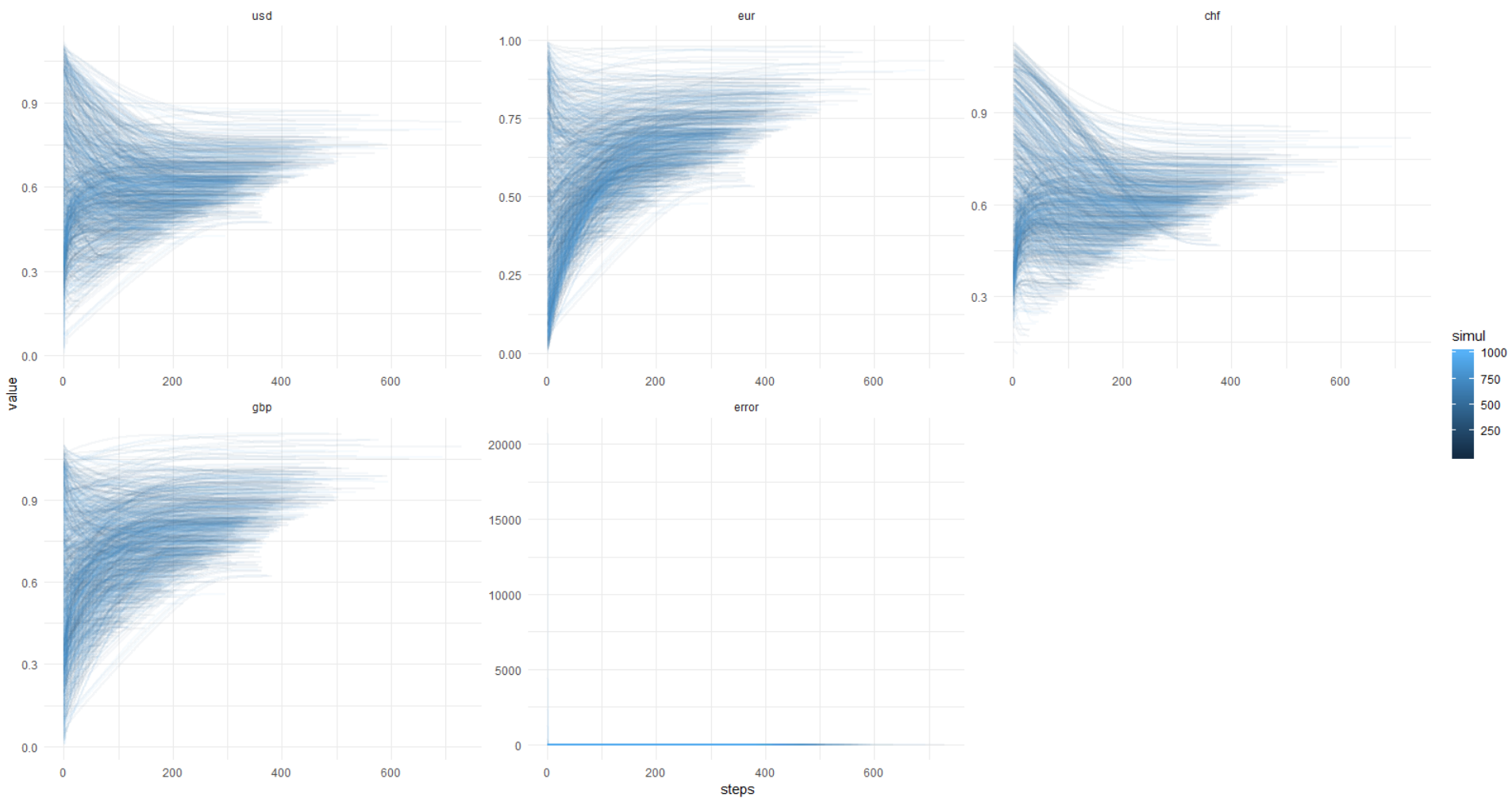
Чтобы вы могли повторить это, ниже я прикладываю полный код.
# clear environment
rm(list = ls()); gc()
## load libs
library(data.table)
library(ggplot2)
library(magrittr)
## set WD --------------------------------
# your dir here ...
## set vars -------------
currs <- c(
'usd',
'eur',
'chf',
'gbp'
)
############
## RUN SIMULATION LOOP -------------------------------
simuls <- 1000L
simul_dt <- data.table()
for(
s in seq_len(simuls)
)
{
#set.seed(111)
usd <- runif(1)
eur <- runif(1)
chf <- runif(1)
gbp <- runif(1)
# snapshot of values at time t
eurusd <- 1.12012
gbpusd <- 1.30890
eurchf <- 1.14135
eurgbp <- 0.85570
gbpchf <- 1.33373
usdchf <- 1.01896
## symbolic task ------------
express <- expression(
(eurusd - eur / usd) ^ 2 +
(gbpusd - gbp / usd) ^ 2 +
(eurchf - eur / chf) ^ 2 +
(eurgbp - eur / gbp) ^ 2 +
(gbpchf - gbp / chf) ^ 2 +
(usdchf - usd / chf) ^ 2
)
## define gradient and iterate to make descent to zero --------------
iter_max <- 1e+3
lr <- 1e-3
min_tolerance <- 0.00001
rm(grad_desc_func)
grad_desc_func <- function(
lr,
curr_list
)
{
derivs <- character(length(curr_list))
deriv_vals <- numeric(length(curr_list))
grads <- numeric(length(curr_list))
# symbolic derivatives
derivs <- sapply(
curr_list,
function(x){
D(express, x)
}
)
# derivative values
deriv_vals <- sapply(
derivs,
function(x){
eval(x)
}
)
# gradient change values
-deriv_vals * lr
}
## get gradient values ----------
progress_list <- list()
for(
i in seq_len(iter_max)
)
{
grad_deltas <- grad_desc_func(lr, curr_list = currs)
currency_vals <- sapply(
currs
, function(x)
{
# update currency values
current_val <- get(x, envir = .GlobalEnv)
new_delta <- grad_deltas[x]
if(new_delta > -1 & new_delta < 1)
{
new_delta = new_delta
} else {
new_delta = sign(new_delta)
}
new_val <- current_val + new_delta
if(new_val > 0 & new_val < 2)
{
new_val = new_val
} else {
new_val = current_val
}
names(new_val) <- NULL
# change values of currencies by gradient descent step in global env
assign(x, new_val , envir = .GlobalEnv)
# save history of values for later plotting
new_val
}
)
progress_list[[i]] <- c(
currency_vals,
eval(express)
)
if(
eval(express) < min_tolerance
)
{
break('solution was found')
}
}
## check results ----------
# print(
# paste0(
# 'Final error: '
# , round(eval(express), 5)
# )
# )
#
# print(
# round(unlist(mget(currs)), 5)
# )
progress_dt <- rbindlist(
lapply(
progress_list
, function(x)
{
as.data.frame(t(x))
}
)
)
colnames(progress_dt)[length(colnames(progress_dt))] <- 'error'
progress_dt[, steps := 1:nrow(progress_dt)]
progress_dt_melt <-
melt(
progress_dt
, id.vars = 'steps'
, measure.vars = colnames(progress_dt)[colnames(progress_dt) != 'steps']
)
progress_dt_melt[, simul := s]
simul_dt <- rbind(
simul_dt
, progress_dt_melt
)
}
ggplot(data = simul_dt) +
facet_wrap(~ variable, scales = 'free') +
geom_line(
aes(
x = steps
, y = value
, group = simul
, color = simul
)
) +
scale_y_log10() +
theme_minimal()
Код на 1000 симуляций работает около минуты.
Заключение
Вот что для меня осталось не понятно:
- можно ли хитрым математическим способом стабилизировать решение;
- будет ли схождение при большем количестве валют и валютных пар;
- если стабильности быть не может, то на каждый новый снэпшот данных наши валюты будут гулять как их вздумается, если не закрепить сид ГПСЧ, а это провал.
Вся затея представляется весьма туманной в отсутствии каких-либо внятных предпосылок и ограничений. Но это было интересно!
Ну, еще хотел сказать, что можно обойтись без МНК, когда данные хитрые, матрицы сингулярные, ну, или, когда теорию плохо знаешь (эхх...).
Спасибо eavprog за изначальный посыл.
Пока!
Автор: Alexey_mosc



