В прошлые выходные в Музее Москвы проходила выставка, в рамках которой Билайн проводил хакатон. Я, на всякий случай, решил сходить. Была предложена интересная задача: дан граф, в вершинах абоненты, в рёбрах записано число звонков одного абонента другому, их продолжительность и число смсок. Данные выглядели вот так:
A,B,x_A,x_B,c_AB,d_AB,c_BA,d_BA,s_AB,s_BA
941235,666804,0,1,1,20,1,22,0,0
604328,367223,1,0,0,0,5,1364,0,0
932768,977234,0,0,1,168,0,0,0,0
395101,677107,0,1,1,160,0,0,0,0
250712,102647,0,0,0,0,3,456,0,0
510653,896558,0,0,139,50954,22,2990,0,0
...
A, B — абоненты, x — оператор, c — число звонков, d — продолжительность разговоров, s — число смсок. Всего ~6 000 000 рёбер. Кроме этого был секретный набор рёбер, которые заранее случайным образом удалили из графа. Предлагалось угадать, что это были за рёбра. То есть по известному набору связей сказать, какие ещё связи могу появиться.
Первым делом я взял 10 000 пар абонентов, между которыми была связь и 10 000 пар, между которыми связи не было. Два основных отличия заключались в следующем:
- Если абоненты соединены, то почти всегда у одного из них оператор 0. Так получается, потому что Билайн обладает информацией только о своих клиентах
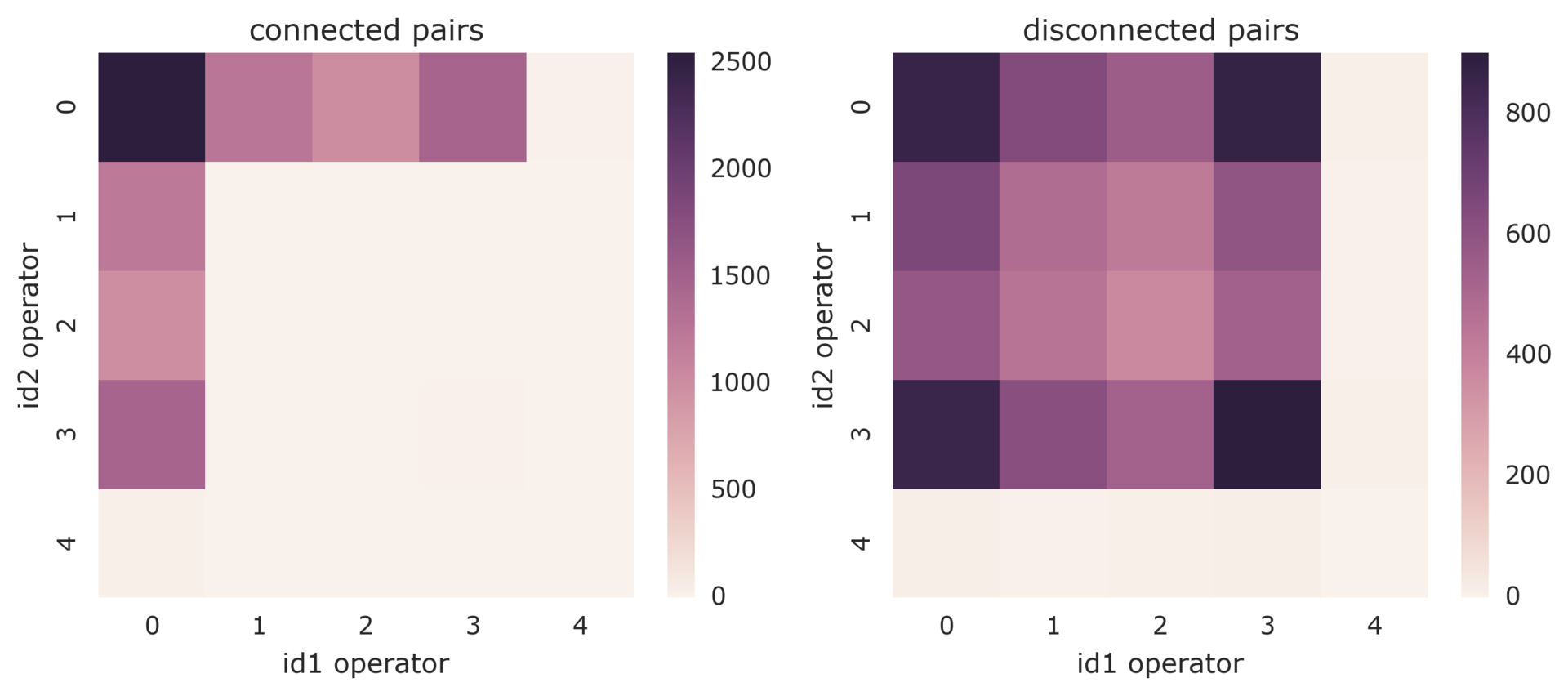
- Если абоненты не соединены, то у них почти всегда нет общих контактов.
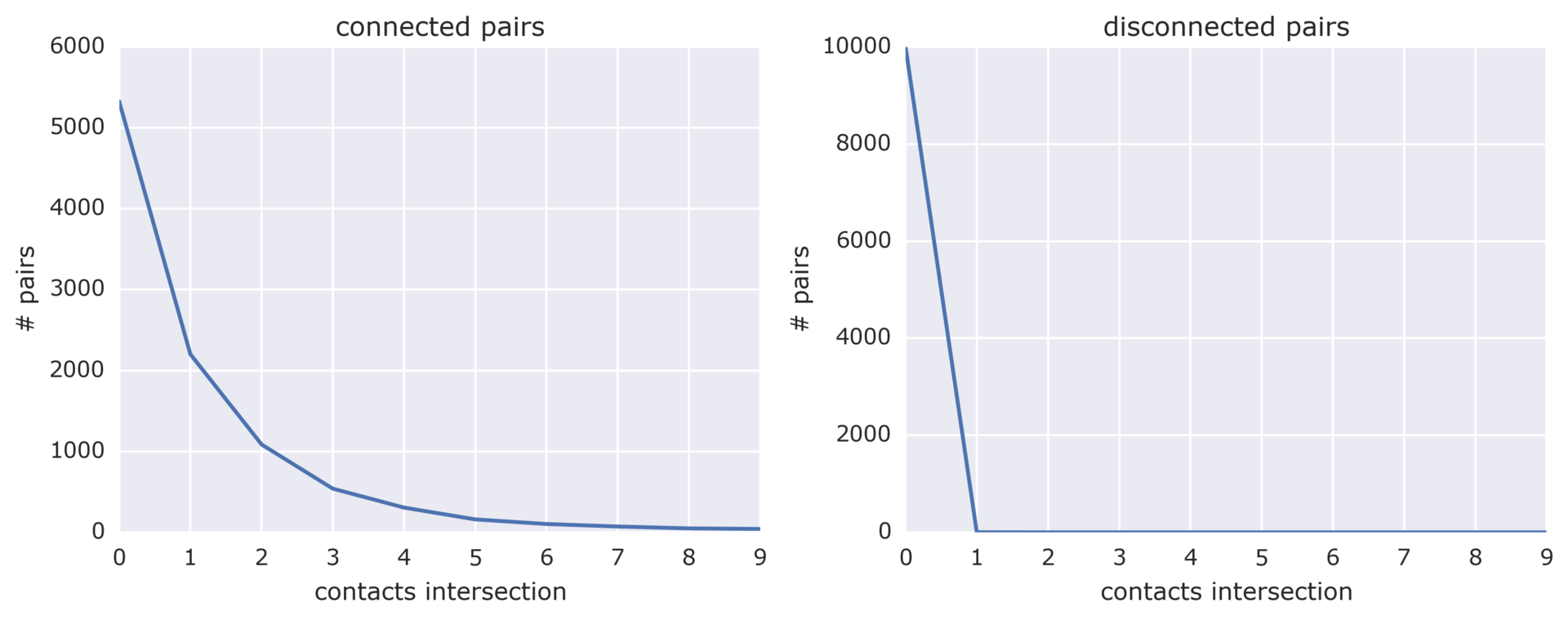
То есть, грубо говоря, моё решение заключалось в следующем: если у пары абонентов, есть хотя бы один общий контакт и хотя бы один из абонентов пользуется оператором 0, то добавляем между ними связь. Проблема заключалась только в том, что в графе было ~1 000 000 абонентов и в лоб проверить сколько общих контактов у каждой пары не получалось. Тут на помощь в очередной раз приходит алгоритм, который уже два раза упоминался на этом сайте, в статьях про поиск похожих групп в ВК и про поиск связанных запросов. Коротко опишу суть. Пускай есть 5 рёбер:
A B
1 10
2 10
3 10
1 11
2 11
Абоненты 1 и 2 пересекаются по двум контактам 10 и 11. Сгруппируем рёбра по B и для каждой группы выпишем все паросочетания A:
1 2
1 3
2 3
1 2
Посчитаем частоту всех паросочетаний и, о чудо, у пары 1, 2 частота 2. Этот алгоритм хорошо ложиться на парадигму мап-редьюс, поэтому здесь опять очень пригождается нано-хадуп на 20 строчек.
Чтобы проверить на сколько качественным получается решение, я убрал из графа 20% рёбер и попробовал их угадать. В качестве метрики организаторы использовали f1 score. Если угадывать случайно f1 получается ~0. Бейзлайн, который предоставили организаторы набирает ~0.02. Моё решение — ~0.07. Оказалось, что при проверке не учитывается направление рёбер, поэтому f1 получается немного выше — ~0.08.
Ещё я попробовал учесть длительность разговоров. Действительно, один общий контакт, с которым оба абонента общались только один раз и недолго, совсем не означает, что абоненты должны быть как-то связаны. Но почему-то на практике никакого прироста в качестве я не получил.
Автор: alexkuku





