Доброго времени суток уважаемые читатели. Недавно в одном проекте мне потребовалось сделать ленточку для блоков. Для примера: очень часто сверху делают ленту с надписью «Fork me on GitHub» или же над каждым элементом в портфолио присутствует лента с датой публикации работы. Лучше покажу пример с официального сайта LESS, так как речь идет о такой маленькой детальке, на которую некоторые могли вообще не обратить внимание.
Данный Ribbon — это изображение внутри ссылки с абсолютным позиционированием. Чем меня не устраивает данный вариант? Во-первых: я очень люблю современные стандарты CSS, с помощью которых можно создать приятный дизайн, используя минимум изображений, а в данном случае лентой может быть обычный блок с transform rotate. Во-вторых: с недавнего времени я смотрю на веб сквозь Retina дисплей и неоптимизированные img сразу же бросаются в глаза, но и разработчикам обращать внимание на какую то ленточку, оптимизировать ее отображение с media queries, мне кажеться, даже немного смешно.
Создадим блок длинной 500px, высотой 50px, с абсолютным позиционированием, сверху, слева. Получится то, что мы видим на изображении ниже в левой части. Далее, повернем блок на -45 градусов, чтобы у нас получилось что-то похожее на Ribbon с LESS. Результат показан в правой части изображения. Наш элемент вращается от своего центра, вследствие чего получается отступ слева, а часть будущей ленты выезжает за рабочую область.
С помощью инспектора мы можем подобрать нужные нам значения для top и -left. Чем меня не устраивает данный вариант? Во-первых — перфекционизм: я хочу, чтобы максимальное количество указанных пикселей (в данном случае 500) отображалось в рабочей области и не выезжало за нее. Во-вторых — лень: я не хочу при изменении позиции (top, right, bottom, left) и градуса наклона вручную подбирать значения, чтобы спрятать все углы.
Геометрия
Как я и сказал, поворот элемента выполняется от центра. Следовательно, и значения отступов измеряются от края рабочей области до центра. Мысленно представим образующиеся фигуры — треугольники, стороны которых нам необходимо вычислить:
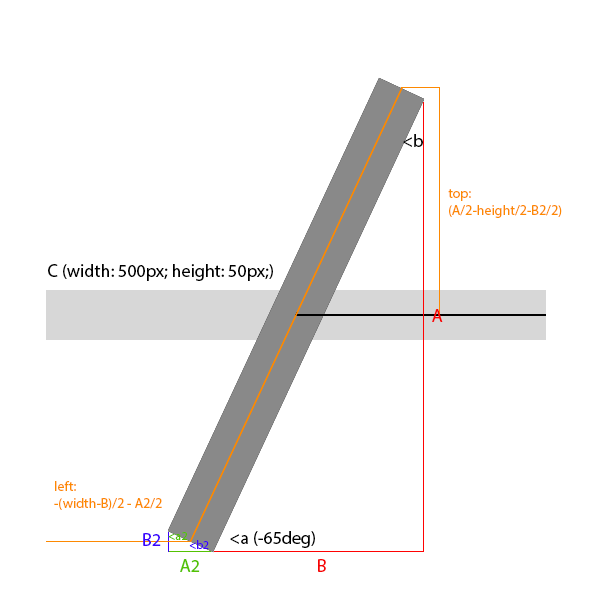
Получилось два треугольника ABC и A2B2C2, стороны которых нам необходимо вычислить. Нам известно, что С = 500px (width), С2 = 50px (height), угол наклона -65 (deg), следовательно, угол a в треугольнике ABC равен 65 градусам, а угол b — 25 градусам (180 — 90 — 65). В треугольнике A2B2C2 углы a2 и b2 равны 65 и 25 градусам соответственно.
Тригонометрия
Все просто. Синус угла равен отношению противолежащего катета к гипотинузе. Следовательно:
A = sin(a) * C или A = sin(65) * 500;
B = sin(b) * C или B = sin(25) * 500;
A2 = sin(a2) * C2 или A2 = sin(65) * 50;
B2 = sin(b2) * C2 или B2 = sing(25) * 50;
LESS
.MojoRibbon(@width, @height, @deg, @valign) {
width: @width;
height: @height;
-webkit-box-sizing: border-box; /* Что бы высота не изменялась при padding */
-moz-box-sizing: border-box;
-ms-box-sizing: border-box;
box-sizing: border-box;
.defineDegree(@deg, @valign) when (@deg < 0) and (@valign = top) {
@degree: -@deg; /* Угол треугольника неотрицательный, вычисляем правильный sin */
top: @countHeight;
left: @countWidth;
-webkit-transform: rotate(@deg);
-moz-transform: rotate(@deg);
-o-transform: rotate(@deg);
-ms-transform: rotate(@deg);
transform: rotate(@deg);
};
.defineDegree(@deg, @valign) when (@deg < 0) and (@valign = bottom) {
@degree: -@deg; /* Угол треугольника неотрицательный, вычисляем правильный sin */
bottom: @countHeight;
right: @countWidth; /* Если угол поворота отрицательный и в вертикали объект позицианируется по нижнему краю, логически правильно в горизонтали позицианировать его по правому краю */
-webkit-transform: rotate(@deg);
-moz-transform: rotate(@deg);
-o-transform: rotate(@deg);
-ms-transform: rotate(@deg);
transform: rotate(@deg);
};
.defineDegree(@deg, @valign) when (@deg > 0) and (@valign = top) {
@degree: @deg;
top: @countHeight;
right: @countWidth;
-webkit-transform: rotate(@degree);
-moz-transform: rotate(@degree);
-o-transform: rotate(@degree);
-ms-transform: rotate(@degree);
transform: rotate(@degree);
};
.defineDegree(@deg, @valign) when (@deg > 0) and (@valign = bottom) {
@degree: @deg;
bottom: @countHeight;
left: @countWidth; /* Если угол поворота положительный и в вертикали объект позицианируется по верхнему краю, логически правильно в горизонтали позицианировать его по левому краю */
-webkit-transform: rotate(@degree);
-moz-transform: rotate(@degree);
-o-transform: rotate(@degree);
-ms-transform: rotate(@degree);
transform: rotate(@degree);
};
.defineDegree(@deg, @valign) when (@deg = 0) {
@degree: @deg;
top: 0;
left: 0;
};
.defineDegree(@deg, @valign);
@angleB: 90-@degree;
@angleB2: @angleB;
@sideA: round(sin(@degree), 3)*@width; /* Сторона А */
@sideB: round(sin(@angleB), 3)*@width; /* Сторона B */
@sideB2: round(sin(@angleB2), 3)*@height; /* Сторона А2 */
@sideA2: round(sin(@degree), 3)*@height; /* Сторона B2 */
@countHeight: @sideA/2 - @height/2 - @sideB2/2;
@countWidth: -((@width)-(@sideB))/2 - @sideA2/2;
}
Большое спасибо всем таким же, как и я CSS занудам за внимание.
Автор: ilusha_sergeevich