Все посты серии:
Часть 1. Введение и настройка
Часть 2. Изучение кода
Часть 3. VST и AU
Часть 4. Цифровой дисторшн
Часть 5. Пресеты и GUI
Часть 6. Синтез сигналов
После улучшений интерфейса пора бы заняться и программированием. В этом посте мы сгенерируем классические синус, пилу, треугольник и меандр.
Начнем с копирования предыдущего проекта скриптом duplicate:
./duplicate.py DigitalDistortion/ Synthesis YourName
В Xcode cнова придется внести изменения в “Run” (Product → Scheme → Edit Scheme…), чтобы сборка запускалась вместе с проектом REAPER, как описывалось ранее. Если он жалуется на то, что не может найти AU, нужно будет изменить имена и ID в resource.h или удалить DigitalDistortion.component.
Класс Oscillator
Материал этой статьи целиком относится к теме DSP. Мы не будем просто писать весь новый код внутри функции ProcessDoubleReplacing. Вместо этого создадим класс Oscillator, будем вызывать его функции из ProcessDoubleReplacing, и он будет наполнять выходной буфер значениями типа double для создания формы волны. Сначала используем интуитивный подход. Позже, столкнувшись с недостатками этого подхода, мы найдем способ добиться лучшего звучания.
Давайте создадим новый класс. На Mac File → New → File…:
На Windows правым кликом по проекту, Add →Class:
Назовем его Oscillator. Убедитесь, что Oscillator.cpp компилируется. В Xcode в таргете AU нажмите на Build Phases. Щелкните по плюсу под Compile Sources и добавьте .cpp файл (это надо будет сделать для каждого таргета):
Давайте напишем заголовок. Вставьте следующий код между #define и #endif в Oscillator.h:
#include <math.h>
enum OscillatorMode {
OSCILLATOR_MODE_SINE,
OSCILLATOR_MODE_SAW,
OSCILLATOR_MODE_SQUARE,
OSCILLATOR_MODE_TRIANGLE
};
class Oscillator {
private:
OscillatorMode mOscillatorMode;
const double mPI;
double mFrequency;
double mPhase;
double mSampleRate;
double mPhaseIncrement;
void updateIncrement();
public:
void setMode(OscillatorMode mode);
void setFrequency(double frequency);
void setSampleRate(double sampleRate);
void generate(double* buffer, int nFrames);
Oscillator() :
mOscillatorMode(OSCILLATOR_MODE_SINE),
mPI(2*acos(0.0)),
mFrequency(440.0),
mPhase(0.0),
mSampleRate(44100.0) { updateIncrement(); };
};
Для обозначения того, какую форму волны будет генерировать наш осциллятор, используем enum. Сейчас по умолчанию будет генерироваться синус, но это можно изменить при помощи функции члена класса setMode.
Объект класса хранит частоту, фазу и частоту семплирования. Значение фазы будет постоянно меняться, т. к. оно содержит в себе информацию о том, в каком моменте цикла генерации формы волны осциллятор находится. Приращение фазы осуществляется каждый семпл. Для простоты представьте себе, что полный цикл одной волны — это окружность. Значение текущего семпла — это точка на окружности. Соедините эту точку с центром окружности: угол, который образован этим отрезком и осью x и есть значение фазы. А угол, на который этот отрезок будет повернут в следующий момент — это приращение фазы.
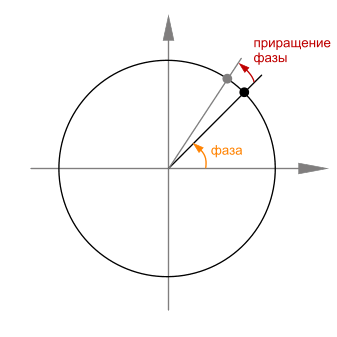
В классе есть разные функции для установки значений параметров (для частоты и частоты семплирования, например). Но самая важная функция — это generate. Это и есть та самая функция, которая заполняет выходной буфер значениями.
Давайте добавим имплементацию этих функций в Oscillator.cpp:
void Oscillator::setMode(OscillatorMode mode) {
mOscillatorMode = mode;
}
void Oscillator::setFrequency(double frequency) {
mFrequency = frequency;
updateIncrement();
}
void Oscillator::setSampleRate(double sampleRate) {
mSampleRate = sampleRate;
updateIncrement();
}
void Oscillator::updateIncrement() {
mPhaseIncrement = mFrequency * 2 * mPI / mSampleRate;
}
Приращение фазы mPhaseIncrement зависит от mFrequency и mSampleRate, так что оно обновляется каждый раз при изменении одного из этих двух параметров. Мы могли бы вычислять его каждый семпл в ProcessDoubleReplacing, но намного лучше делать это здесь.
Функция generate на данный момент выглядит так:
void Oscillator::generate(double* buffer, int nFrames) {
const double twoPI = 2 * mPI;
switch (mOscillatorMode) {
case OSCILLATOR_MODE_SINE:
// ...
break;
case OSCILLATOR_MODE_SAW:
// ...
break;
case OSCILLATOR_MODE_SQUARE:
// ...
break;
case OSCILLATOR_MODE_TRIANGLE:
// ...
break;
}
}
Эта функция будет вызываться каждый раз, когда вызывается ProcessDoubleReplacing. Switch используется для того, чтобы в зависимости от нужной формы волны исполнялся соответствующий код.
Генерация формы волны
Для синуса все просто:
case OSCILLATOR_MODE_SINE:
for (int i = 0; i < nFrames; i++) {
buffer[i] = sin(mPhase);
mPhase += mPhaseIncrement;
while (mPhase >= twoPI) {
mPhase -= twoPI;
}
}
break;
Обратите внимание, что мы не используем mFrequency и mSampleRate. Мы даем приращение mPhase и ограничиваем его между 0 и twoPI. Единственной «сложной» операцией тут является вызов функции sin(), которая выполняется на уровне железа на большинстве систем.
Так выглядит пила:
case OSCILLATOR_MODE_SAW:
for (int i = 0; i < nFrames; i++) {
buffer[i] = 1.0 - (2.0 * mPhase / twoPI);
mPhase += mPhaseIncrement;
while (mPhase >= twoPI) {
mPhase -= twoPI;
}
}
break;
Опять же, интересный момент с записью в буфер. Когда я вижу такие вычисления, мне удобно разбивать их на части:
mPhaseвозрастает, начиная с0и соскакивает обратно в ноль по достижении значенияtwoPI.- Далее,
(mPhase / twoPI)возрастает с0до1и соскакивает обратно в ноль. - Значит,
(2.0 * mPhase / twoPI)возрастает от0, и соскакивает обратно, как только достигает двух. - Когда
mPhaseравно0, выражение1.0 - (2.0 * mPhase / twoPI)равно1. ПокаmPhaseвозрастает, значение этого выражения падает и, как только достигает-1, подскакивает до1.
Ну вот, у нас есть нисходящая («левая») пила!
Условие while, казалось бы, избыточно — оно будет встречаться в каждом case. Но если сделать иначе, тогда придется включить switch в цикл. Так мы даже избавимся от избыточного for, но тогда switch будет выполняться чаще, чем необходимо.
Часто в программировании мы предпочитаем лаконичность и читаемость кода производительности. Но DSP код, который выполняется 44100 (или даже 96000) раз в секунду может быть и исключением из этого правила. Помимо этого, не забывайте, что компилятор оптимизирует много всего без вашего ведома, и то, что может казаться «кучей работы» для программиста может быть элементарной вещью в сравнении с теми процессами, о которых вы даже не задумываетесь.
Следующий в очереди — меандр:
case OSCILLATOR_MODE_SQUARE:
for (int i = 0; i < nFrames; i++) {
if (mPhase <= mPI) {
buffer[i] = 1.0;
} else {
buffer[i] = -1.0;
}
mPhase += mPhaseIncrement;
while (mPhase >= twoPI) {
mPhase -= twoPI;
}
}
break;
Вторая половина этого кода вам уже известна. Каждый цикл длиной в twoPI. Тело условного оператора if устанавливает первую половину цикла равной 1, вторую -1. Когда mPhase становится больше mPI, в форме волны появляется резкий скачок. Так выглядит меандр.
Треугольник немного сложнее:
case OSCILLATOR_MODE_TRIANGLE:
for (int i = 0; i < nFrames; i++) {
double value = -1.0 + (2.0 * mPhase / twoPI);
buffer[i] = 2.0 * (fabs(value) - 0.5);
mPhase += mPhaseIncrement;
while (mPhase >= twoPI) {
mPhase -= twoPI;
}
}
break;
Если вы разберете по частям -1.0 + (2.0 * mPhase / twoPI), как я это сделал раньше, то увидите, что это противоположность пиле. Абсолютное значение (fabs) восходящей пилы означает, что все значения ниже 0 будут инвертированы (перевернуты относительно оси x).
Значит, результирующее значение будет сначала возрастать, а потом убывать. Вычитание 0.5 выравнивает форму волны относительно нуля. Умножение на 2.0 масштабирует значение, и оно меняется от -1 до 1. Вот и треугольник.
Давайте уже используем наш осциллятор! Включите Oscillator.h и добавьте член Oscillator в класс Synthesis:
// ...
#include "Oscillator.h"
class Synthesis : public IPlug
{
// ...
private:
double mFrequency;
void CreatePresets();
Oscillator mOscillator;
};
Также нам надо переименовать mThreshold в mFrequency.
Теперь поменяйте параметры инициализации в конструкторе:
GetParam(kFrequency)->InitDouble("Frequency", 440.0, 50.0, 20000.0, 0.01, "Hz");
GetParam(kFrequency)->SetShape(2.0);
Покрутим ручку, протестируем класс. Будем менять частоту осциллятора от 50 Гц до 20 кГц (по умолчанию поставим 440).
Измените функцию createPresets:
void Synthesis::CreatePresets() {
MakePreset("clean", 440.0);
}
Нам нужно передать осциллятору, какая частота семплирования сейчас используется. Это надо сделать в функции Reset:
void Synthesis::Reset()
{
TRACE;
IMutexLock lock(this);
mOscillator.setSampleRate(GetSampleRate());
}
Если мы этого не сделаем и у осциллятора будет неверно задана частота семплирования, он будет генерировать те же формы волны, но частоты будут неправильными, т. к. будет вычислено неправильное приращение фазы. Функция-член GetSampleRate наследуется из класса IPlugBase.
OnParamChange тоже надо отредактировать, чтобы можно было менять частоту ручкой:
void Synthesis::OnParamChange(int paramIdx)
{
IMutexLock lock(this);
switch (paramIdx)
{
case kFrequency:
mOscillator.setFrequency(GetParam(kFrequency)->Value());
break;
default:
break;
}
}
Ну и наконец, надо использовать осциллятор в ProcessDoubleReplacing:
void Synthesis::ProcessDoubleReplacing(double** inputs,
double** outputs,
int nFrames) {
// Mutex is already locked for us.
double *leftOutput = outputs[0];
double *rightOutput = outputs[1];
mOscillator.generate(leftOutput, nFrames);
// Copy left buffer into right buffer:
for (int s = 0; s < nFrames; ++s) {
rightOutput[s] = leftOutput[s];
}
}
По сути mOscillator заполняет буфер левого канала, и мы просто копируем эти значения в буфер правого.
Давайте послушаем, как это звучит! Запускайте. Если в Xcode вылетают ошибки линкера, проверьте, добавили ли вы Oscillator.cpp в Compile Sources. Когда наша поделка запустится, будет слышен ровный тон. Покрутите ручку, и частота должна меняться.
Теперь поменяйте mOscillatorMode в Oscillator.h на этапе инициализации в конструкторе:
Oscillator() :
mOscillatorMode(OSCILLATOR_MODE_SAW),
mPI(2*acos(0.0)),
mFrequency(440.0),
mPhase(0.0),
mSampleRate(44100.0) { updateIncrement(); };
Перезапустите код, и теперь будет более резкий звук. Поиграйтесь с OSCILLATOR_MODE_SQUARE и OSCILLATOR_MODE_TRIANGLE, у них разные тембры.
Со всеми формами волны, кроме синуса, можно заметить, что на высоких частотах появляются странные шумы. Появляются дополнительные тоны даже ниже основной частоты. Они звучат негармонично, и когда крутишь ручку вверх и вниз, эти тоны смещаются в противоположных направлениях о_О
Алиасинг
Как мы уже видели в коде меандра, когда фаза возрастает до значения большего, чем два пи, в форме волны возникает мгновенный скачок от положительного максимума в текущем семпле до отрицательного в следующем. Противоположный скачок возникает, когда из mPhase вычитается twoPI и значение выражения снова становится меньше mPI. Основная идея в том, что резкие скачки сигнала означают, что в нем содержится много высокочастотных компонент.
Представьте себе, что вас попросили собрать этот скачок, используя только синусоидальные волны. Учитывая, что они гладкие, вам понадобится множество высокочастотных синусов. Вообще для создания идеального скачка теоретически понадобится бесконечное количество высокочастотных компонент, каждая со все большей частотой. Вот то же самое происходит при генерации меандра, пилы и треугольника.
Но в вычислительной технике все — конечное. Оперативная память и жесткий диск имеют конечный объем, так что для записи одной секунды звука компьютер может использовать только конечное количество значений, чтобы сохранить эту секунду. Это число (частота семплирования) может быть любым, но стандартами являются 44100, 48000 и 96000 семплов в секунду. Реже используются 176400 и 192000. Сигнал, представленный конечным количеством семплов, называется дискретным.
Чтобы описать сигнал, скачущий между -1 и 1, понадобится как минимум два семпла на цикл: один для -1, другой для 1. Значит, если семплировать с частотой 44100 раз в секунду, самой высокой корректно записанной частотой будет 22050 Гц (почитайте про частоту Найквиста)
Так что дискретным сигналом описать идеальный меандр, пилу или треугольник невозможно. Если мы все же будем пытаться это делать, то очень скоро столкнемся с эффектом алиасинга. Подробнее можно почитать здесь.
Так как же мы можем сгенерировать самую лучшую форму волны для заданной частоты дискретизации без эффектов алиасинга? «Самая лучшая» в данном случае означает «самая близкая к той, которую мы описали выше». Частота Найквиста — это некоторое ограничение в частотном диапазоне. Это ограничение означает не то, что сигнал не должен иметь пиков круче X, а то, что в сигнале не должно присутствовать частот выше X Гц. Так что нам надо переключиться в частотное представление сигнала для решения подобных задач. Мы сделаем это немного позже, а пока что — в следующем посте — нам предстоит разобраться, как читать MIDI.
Код из этого поста можно скачать здесь.
Автор: 1eqinfinity






