Даже не являясь навигатором, 2ГИС собирает и показывает информацию о пробках. Во-первых, это необходимо для построения оптимальных маршрутов, а во-вторых — такие данные очень нужны пользователям в больших городах.
В 2ГИС сервис пробок появился в сентябре 2011 года и сегодня работает в пяти городах (Новосибирск, Санкт-Петербург, Красноярск, Уфа, Казань). В планах на ближайшее будущее — запустить пробки во всех городах-миллионниках.
Под катом история про то, с какими проблемами мы столкнулись и как их решили.
Основа «Пробок» — это данные, а именно точки. Отдельная точка несёт следующую основную информацию:
- идентификатор проекта(города);
- время регистрации;
- координаты;
- моментальная скорость;
- направление движения в момент регистрации.
Такие точки мы получаем от наших поставщиков данных, а также пользователей мобильной версии 2ГИС. Перед тем как поучаствовать в расчёте, данные попадают в хранилище сырых данных, основанное на MongoDB.
Что такое «притяжка точек» и зачем она нужна:
Автомобильная пробка не существует сама по себе, а обычно расположена на какой-нибудь дороге. Сами точки не несут информации о том, по какому участку проезжало устройство в момент регистрации, поэтому их необходимо наложить на дорожную сеть.
Таким образом, притяжка точек — процесс соотнесения каждой точке участка дороги, на котором она была зарегистрирована, с учётом её скорости и направления движения.
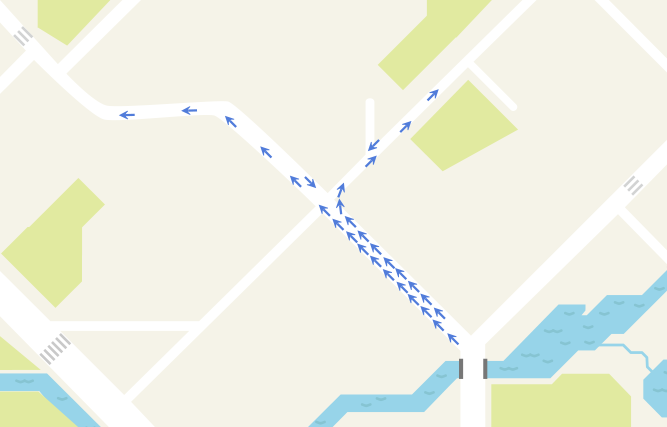
Давайте возьмём одну точку (рисунок a), и попробуем определить, на каком участке дороги она была зарегистрирована.
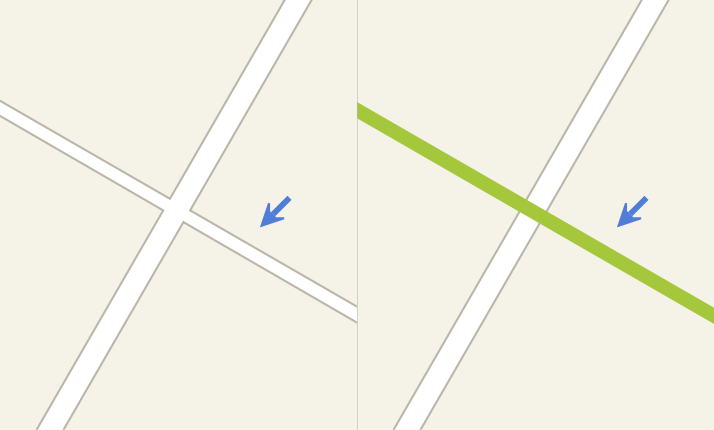
Понятно, что нужный участок дороги где-то рядом с точкой, поэтому сразу встаёт задача поиска ближайшего сегмента дорожной сети в некотором радиусе(например, 20 метров).
В данном случае прямое и обратное направления ближайшего сегмента (рисунок b) очень не совпадает с направлением, которое зафиксировало устройство в момент регистрации точки (показано стрелкой), поэтому этот сегмент — не то, что мы искали. Из рисунка видно, что правильный ответ оказался рядом. Такие ситуации могут возникать, например, из-за существенной погрешности устройств (трекеров). На более сложных (возможно, многоуровневых) развязках они возникают постоянно, поэтому такой поиск не подойдёт.
Модифицируем его следующим образом: будем искать не ближайший сегмент, а все сегементы в радиусе. В результате такого поиска получим сразу несколько сегментов, и уже с учётом их направления, расстояния до них, и прочих атрибутов сможем более правильно выбрать искомый сегмент.
Всё бы хорошо, но дорожая сеть в некоторых городах очень большая, сотни тысяч сегментов, а точек, которые нужно притянуть, — миллионы за несколько минут, так что наравне с качеством решения задачи встаёт вопрос и скорости поиска.
Что было раньше
Изначально, не было задачи считать онлайн-пробки, а была задача обработать данные за месяц с тем, чтобы в наших офлайн-продуктах выставить среднемесячные скорости по дорогам и более реалистично показывать время проезда.
Данные от поставщиков аггрегировались в центральном хранилище.
Поскольку центральное хранилище данных использует PostgreSQL, то и эта задача на ранних этапах решалась с помощью расширения PostGIS.
Упрощенно, алгоритм был примерно следующий:
- На этапе подготовки вокруг всех ребер графа строились полигоны (функция ST_Buffer), ширина (разная для разных классов дорог) которых определяла допустимое отклонение.
- Точка проверялись на попадание в эти полигоны и выбирались допустимые ребра.
- На все допустимые ребра строилась проекция точки (функция ST_ClosestPoint) и мы получали сортировку допустимых ребер по расстоянию.
- Используя сортировку по расстоянию, проверяя азимут точки и азимут сегмента ребра, класс и ширину дороги и предыдущие притянутые точки от данного устройства мы определяли вероятное ребро графа и проекцию точки на это ребро считали притянутой точкой и записывали в базу.
Вся эта кухня на хранимых процедурах работала, хотя и не очень быстро, но и срочности никакой в этих данных не было, так как задача решалась для офлайн-продуктов.
На среднем сервере, скорость получалась около 2 000 точек в секунду.
C появлением режима «Онлайн» этого решения стало недостаточно: данные обновляются каждые пять минут, так что полный цикл обработки данных должен укладываться в это время. С увеличением объёма данных этот этап стал выполняться настолько долго, что вписать в пять минут весь цикл было затруднительно даже на весьма мощном «железе».
Пришло время реализовать уже давно назревавшую идею — реализация расчётов на C++.
Поиск быстрых решений
Параллельно мы начали разрабатывать 2 решения — одно на основе библиотеки GEOS, а второе на полностью с нуля на основании квадродеревьев.
О GEOS
Это решение появилось первым, так как использовало готовую библиотеку GEOS, которую, кстати, использует и PostGIS.
Для поиска ближайших сегментов использовались Quadtree индексы из этой библиотеки.
Для этого в дерево загружаются все сегменты дорожного графа, указывается область попадания вокруг точки и на выходе мы имеем набор сегментов, которые пересекают область попадания, затем сегменты сортируются по расстоянию до точки и выбирается ближайщий.
Собственная реализация квадродеревьев
Эта реализация появилась второй, но (немного забегая вперед) получилась немного более удачной.
Сначала несколько общих определений, чтобы добавить ясности.
Квадродерево — это дерево, в котором каждый внутренний узел имеет четыре потомка.
Квадродерево позволяет рекурсивно разбить двухмерное пространство на четыре квадранта (области).
Квадродеревья способны хранить информацию о разных типах данных, однако нас интересует хранение сегментов(отрезков), поскольку дорожную сеть можно просто представить именно с помощью сегментов.
Для этого мы использовали оптимизированную для хранения сегментов версию PM Quadtree — Polygonal Map Random Quadtree.
PMR Quadtree:
- Использует вероятностное правило разбиения;
- Каждый узел содержит переменное количество сегментов;
- Каждый сегмент вставляется во все узлы, которые пересекает;
- Если узел содержит количество сегментов, превышающее ограничение, то происходит разбиение(только однажды) на 4 дочерних узла;
- Хорошо подходит для задачи поиска ближайшего сегмента.
Минусы:
- Возможна разбалансировка дерева.
Каждый узел дерева представляет некоторую область(например, квадратную) и содержит следующую информацию:
- Глубину;
- Координаты области;
- Четыре потомка, если узел внутренний;
- Сегменты, если узел внешний.
Узел хранит только те сегменты, которые пересекают его область. Количество сегментов в узле переменно.
Построение
Построение структуры данных представляет собой процесс последовательной вставки сегментов в дерево. Изначально дерево пустое.
Аналогично алгоритмам построения многих других иерархических структур данных, алгоритм построения PMR Quadtree основан на обходе сверху-вниз (top-down traversal). Другими словами, начиная с корневого узла мы посещаем все дочерние узлы, пересекающиеся с сегментом, и добавляем этот сегмент во все встретившиеся внешние узлы.
Ключевой аспект PMR Quadtree — правило разбиения, то есть условие, при котором узел делится. Для этой цели используется некоторый параметр t, ограничивающий количество сегментов, которое может содержаться в узле.
Если количество сегментов, которое пересекается с областью, превышает t и если не достигнут максимальный уровень глубины, то эта область делится на четыре дочерних, а все сегменты, которые с ним пересекались, вставляются в новые дочерние узлы. Стоить заметить, что сразу после разбиения дочерние узлы не разбиваются снова, даже если количество сегментов в узле превышает t. Это позволяет избежать чрезмерного разбиения и приводит к вероятностному поведению в том смысле, что порядок, в котором объекты вставляются, влияет на структуру полученного дерева.
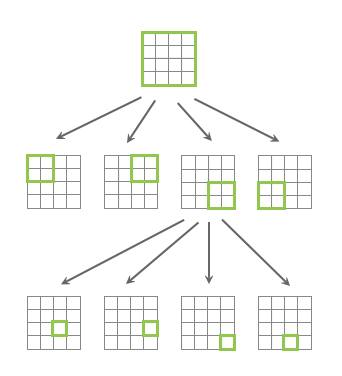
Визуализация


Поиск в дереве
Для поиска будем использовать очередь с приоритетом.
В очередь будем помещать объекты трёх типов:
- внутренние узлы;
- внешние узлы;
- сегменты.
Ключ в очереди — расстояние до исходной точки. Изначально очередь содержит только корневой узел.
Теперь на каждом шаге будем брать из очереди объект с минимальным расстоянием и в зависимости от его типа проводить соответствующие операции:
- Внутренний узел. Добавим в очередь каждый из четырёх потомков, если расстояние от него до точки не превышает R
- Внешний узел. Добавим в очередь все содержащиеся в нём сегменты, расстояние до которых от точки не превышает R
- Сегмент. Найден ответ на задачу.
Аналогично можно решить задачу нескольких ближайших сегментов в радиусе.
Сравнение
Сравнив реализацию на GEOS и собственную, мы были приятно удивлены:
На одном и том же железе для 300 000 сегментов:
| GEOS | PMR Quadtree | |
|---|---|---|
| Построение дерева | 2 секунды | 0,2 секунды |
| Потребление памяти | 200 Мб | 50 Мб |
| Притяжка точек | 35 500 точек в секунду | 383 500 точек в секунду |
В итоге собственное решение и легло в основу нового сервиса притяжки точек и позволяет на среднем сервере делать притяжку точек от всех поставщиков по всей России.
Заключение
В итоге, перейдя от PostGIS к узкоспециализированному решению на C++ мы получили ускорение с 2к до 380к (в 190 раз).
Пишите узкоспециализированные велосипеды!
Как работает сервис пробок можно посмотреть прямо сейчас или установив 2ГИС на iOS или Android.
Автор: stanislav_p