Одной из главных проблем при съёмке астрофотографий являются разнообразные шумы. Не буду подробно останавливаться на том, откуда они берутся и какие компоненты в них присутствуют. Об этом уже есть хорошая серия статей на Хабре. Здесь я только резюмирую основной способ борьбы с шумом: нужно снять несколько кадров одной и той же области неба (чем больше, тем лучше) и усреднить сигнал с соответствующих пикселей.
Но какие пиксели на разных кадрах считать соответствующими? Если бы можно было гарантировать, что объекты между кадрами не сдвинутся ни на пиксель, то всё было бы предельно ясно: просто суммируем одни и те же пиксели на матрице. Но что делать, когда слежение неидеально, или съёмка вовсе ведётся с неподвижного штатива? Тогда звёзды и другие небесные тела будут смещаться, и перед сложением кадры нужно будет правильно наложить друг на друга. Эта статья посвящена тому, как это сделать.

Итак, допустим, что мы сняли серию кадров ночного неба фотоаппаратом с широкоугольным объективом с неподвижного штатива. Широкоугольность означает, что в поле зрения находится большой участок неба, где присутствуют звёзды разных склонений. За счёт суточного вращения неба звёзды описывают круги около полюса. После проекции на плоскую матрицу их траектории оказываются весьма замысловатыми, как например на этом кадре:

На астрофотографиях присутствуют естественные ориентиры для выравнивания — это звёзды. К сожалению, звёзды, бывшие на первом снимке в одних местах, на втором окажутся совершенно в других, причем смещения у разных звёзд будут неодинаковы. Таким образом задачу по совмещению астрофотографий придётся разбить на три подзадачи:
-
Найти звёзды на всех снимках серии.
-
Отождествить звёзды на разных снимках
-
Пользуясь полученной информацией, наложить кадры друг на друга.
Шаг 1. Ищем звёзды
На этом шаге мы будем работать с изображением в градациях серого. Если оно изначально цветное, его нужно будет сначала сконвертировать в чёрно-белое.
Найти звёзды на снимке довольно просто. Достаточно вспомнить, что на изображении звезда выглядит, как группа смежных пикселей, чья яркость превышает фон. Создадим структуру, которая будет хранить информацию о звезде. Нам нужно будет знать прямоугольник, в который вписывается звезда, положение её центра (может не совпадать с центром прямоугольника), суммарная яркость всех пикселей, а также их количество.
struct Star
{
Rect rect;
PointF center;
double luminance = 0.0;
uint32_t pixelCount = 0;
};За фоновое значение можно взять медианную яркость пикселя по всему изображению, но чтобы отсечь случайные всплески из-за шумов, повысим этот порог на некоторый процент. На сколько конкретно процентов повысить - зависит от количества звёзд на снимке. Если звёзд много, то можно взять порог повыше, если мало — то наоборот, понизить.
auto median = data.begin() + data.size() / 2;
std::nth_element(data.begin(), median, data.end());
auto threshold = ChannelType( std::min(
uint32_t(*median * (1 + _thresholdPercent / 100.0f)),
uint32_t(std::numeric_limits<ChannelType>::max())) );Далее мы последовательно обходим все пиксели, и если натыкаемся на пиксель с яркостью выше пороговой, добавляем звезду.
auto pData = pGrayBitmap->GetScanline(0);
for (int i = roi.y; i < roi.y + roi.height; ++i)
for (int j = roi.x; j < roi.x + roi.width; ++j)
{
if (pData[i * w + j] > threshold)
{
stars.emplace_back(
Rect{ .x = int32_t( j ), .y = int32_t( i ), .width = 1, .height = 1 }
);
auto& star = stars.back();
InspectStar(star, threshold, pData, j, i, w, h, roi);
if (star.rect.width >= _minStarSize &&
star.rect.width <= _maxStarSize &&
star.rect.height >= _minStarSize &&
star.rect.height <= _maxStarSize)
{
star.center.x /= star.luminance;
star.center.y /= star.luminance;
}
}
}
Найдя один пиксель, превышающий заданный порог, нужно проверить его соседей. Причем верхних соседей и соседа слева проверять не нужно, те пиксели мы уже прошли. Остаются еще четыре соседних пикселя. Если сосед тоже ярче порога, то продолжаем рекурсивный обход.
Для каждого найденного пикселя мы вычисляем, насколько его яркость превышает порог. Далее это превышение добавляется к суммарной яркости звезды, а произведение с координатой добавляется к координате центра. В конце их нужно будет разделить на суммарную яркость звезды. Чтобы этот пиксель не поверять повторно, обнулим его. Так как мы тут работаем с копией данных, на исходной картинке это не отразится.
Код обхода звезды
template <typename ChannelType>
void InspectStar(Star& star, ChannelType threshold, ChannelType* pData, int x, int y, int w, int h, Rect roi)
{
++star.pixelCount;
auto pixelLuminance = pData[y * w + x] - threshold;
star.luminance += pixelLuminance;
star.center.x += x * pixelLuminance;
star.center.y += y * pixelLuminance;
pData[y * w + x] = 0;
if (x + 1 < roi.x + roi.width && pData[y * w + x + 1] > threshold)
{
star.rect.ExpandRight(x + 1);
InspectStar(star, threshold, pData, x + 1, y, w, h, roi);
}
if (x + 1 < roi.x + roi.width && y + 1 < roi.y + roi.height && pData[(y + 1) * w + x + 1] > threshold)
{
star.rect.ExpandRight(x + 1);
star.rect.ExpandDown(y + 1);
InspectStar(star, threshold, pData, x + 1, y + 1, w, h, roi);
}
if (y + 1 < roi.y + roi.height && pData[(y + 1) * w + x] > threshold)
{
star.rect.ExpandDown(y + 1);
InspectStar(star, threshold, pData, x, y + 1, w, h, roi);
}
if (x > roi.x && y + 1 < roi.y + roi.height && pData[(y + 1) * w + x - 1] > threshold)
{
star.rect.ExpandDown(y + 1);
star.rect.ExpandLeft(x - 1);
InspectStar(star, threshold, pData, x - 1, y + 1, w, h, roi);
}
}После того, как мы получили полный список звёзд, отсортируем его по убыванию яркости и нормируем яркости всех звёзд.
std::sort(stars.begin(), stars.end(), [](auto& a, auto& b) {return a.luminance > b.luminance; });
auto maxLuminance = stars[0].luminance;
for (auto& star : stars)
star.luminance /= maxLuminance;Шаг 2. Отождествляем звёзды
Теперь у нас есть списки звёзд для каждого кадра. Выберем один опорный кадр и сопоставим ему звёзды на всех других изображениях. Обычно все кадры сняты с одним и тем же фокусным расстоянием, так что можем исходить из предположения, что угловые расстояния между звёздами между кадрами не меняется.
Выберем одну пару звёзд из опорного списка и другую пару из целевого списка. Если разница расстояний между ними больше допустимой погрешности, то отбрасываем эту комбинацию и переходим к следующей. Если же разница укладывается в погрешность, то нужно вычислить аффинную матрицу, которая отображает целевую пару точек в опорную. Проще говоря — угол и сдвиг, с которыми нужно наложить целевой снимок на опорный, чтобы данные пары звёзд совпали. Выполнив такое наложение, смотрим, сколько целевых звёзд совпали с опорными. И снова переходим к следующей комбинации пар.
Код алгоритма
for (size_t i = 0; i < refLim - 1; ++i)
for (size_t j = i + 1; j < refLim; ++j)
{
PointFPair refPair{ _refStars[i].center, _refStars[j].center };
for (size_t k = 0; k < targetLim - 1; ++k)
for (size_t l = k + 1; l < targetLim; ++l)
{
PointFPair targetPair{ _targetStars[k].center, _targetStars[l].center };
auto penalty = std::fabs(refPair.first.Distance(refPair.second) - targetPair.first.Distance(targetPair.second));
if (penalty > _eps)
continue;
IndexMap temp {{k, i}, {l, j}};
auto transform = CalculateTransform(refPair, targetPair);
BruteForceCheckTransform(refLim, targetLim, temp, transform);
if (temp.size() > res.first.size())
{
res.first = temp;
res.second = transform;
}
temp = IndexMap{ {k, j}, {l, i} };
transform = CalculateTransform(refPair, { _targetStars[l].center , _targetStars[k].center });
BruteForceCheckTransform(refLim, targetLim, temp, transform);
if (temp.size() > res.first.size())
{
res.first = temp;
res.second = transform;
}
}
}
...
Среди всех наложений выбираем то, которое даёт больше всего совпадений звёзд. Именно такую матрицу нужно применить к координатам пикселей целевого изображения, чтобы суммировать сигнал.
Проверяем матрицу
void FastAligner::BruteForceCheckTransform(const size_t refLim, const size_t targetLim, IndexMap& temp, const agg::trans_affine& transform)
{
size_t refs[2] = { temp.begin()->second, std::next(temp.begin())->second };
size_t targets[2] = { temp.begin()->first, std::next(temp.begin())->first };
for (size_t i = 0; i < targetLim; ++i)
{
if (targets[0] == i || targets[1] == i)
continue;
auto transformedRefPoint = _targetStars[i].center;
transform.transform(&transformedRefPoint.x, &transformedRefPoint.y);
for (size_t j = 0; j < refLim; ++j)
{
if (refs[0] == j || refs[1] == j)
continue;
if (transformedRefPoint.Distance(_refStars[j].center) > _eps)
continue;
temp[i] = j;
break;
}
}
}Рассмотрим искусственный пример (с картинками)
Пусть на опорном кадре мы обнаружили 5 звёзд, а на целевом — 6. Расположены они так, как показано на иллюстрации (синий цвет — опорные звезды, розовый — целевые). Многие пары мы не сможем совместить, потому что между звездами разное расстояние, например (r0, r1) и (t0, t5).
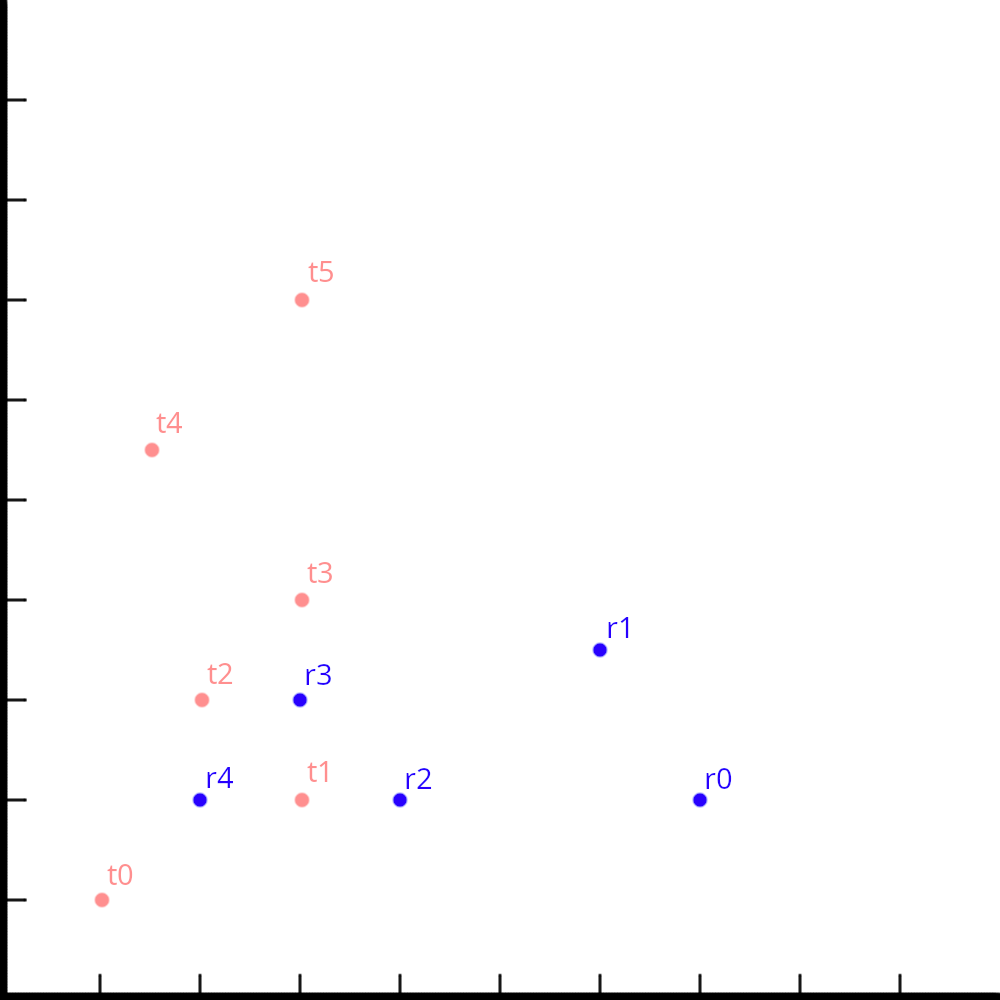
Мы можем совместить пары (r2, r3) и (t1, t2), но тогда кроме этих звёзд больше никакие не совпадут.
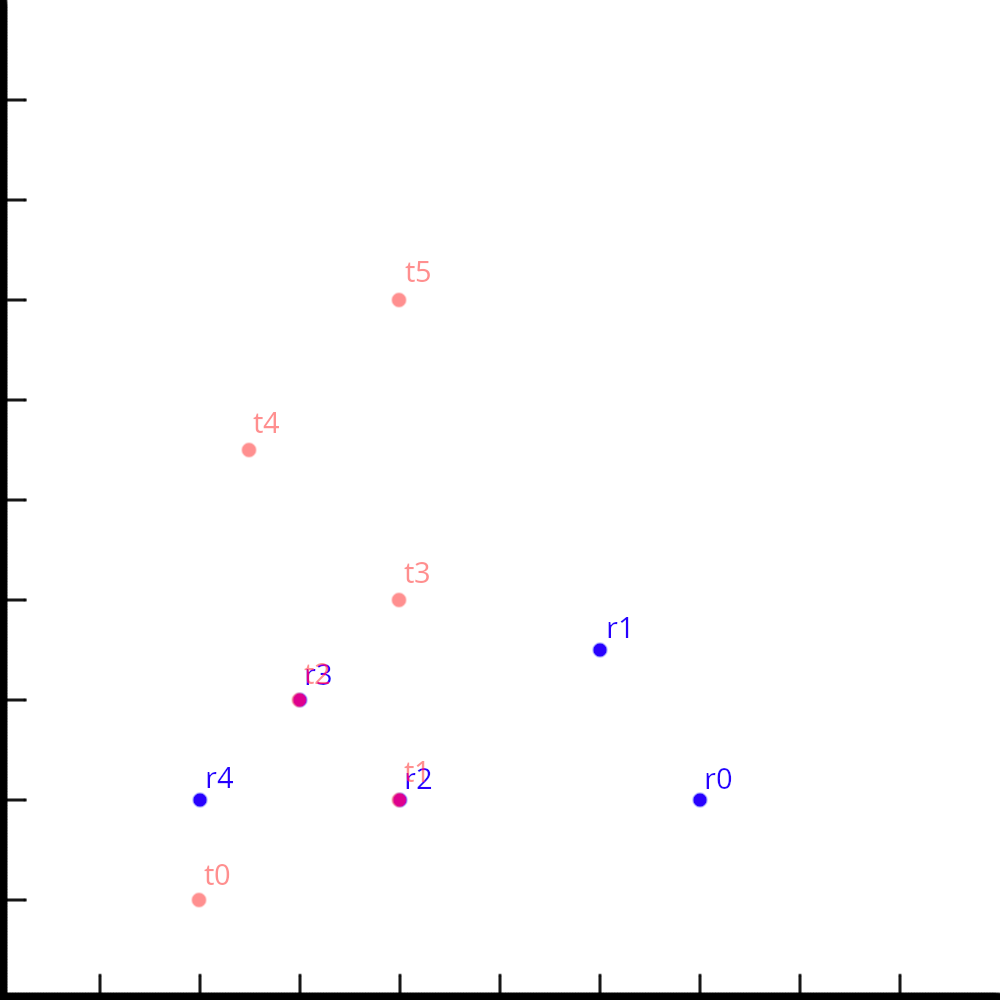
А вот, совмещая пары (r0, r4) и (t1, t5), мы получим наибольшее число совпадений, а именно 4.
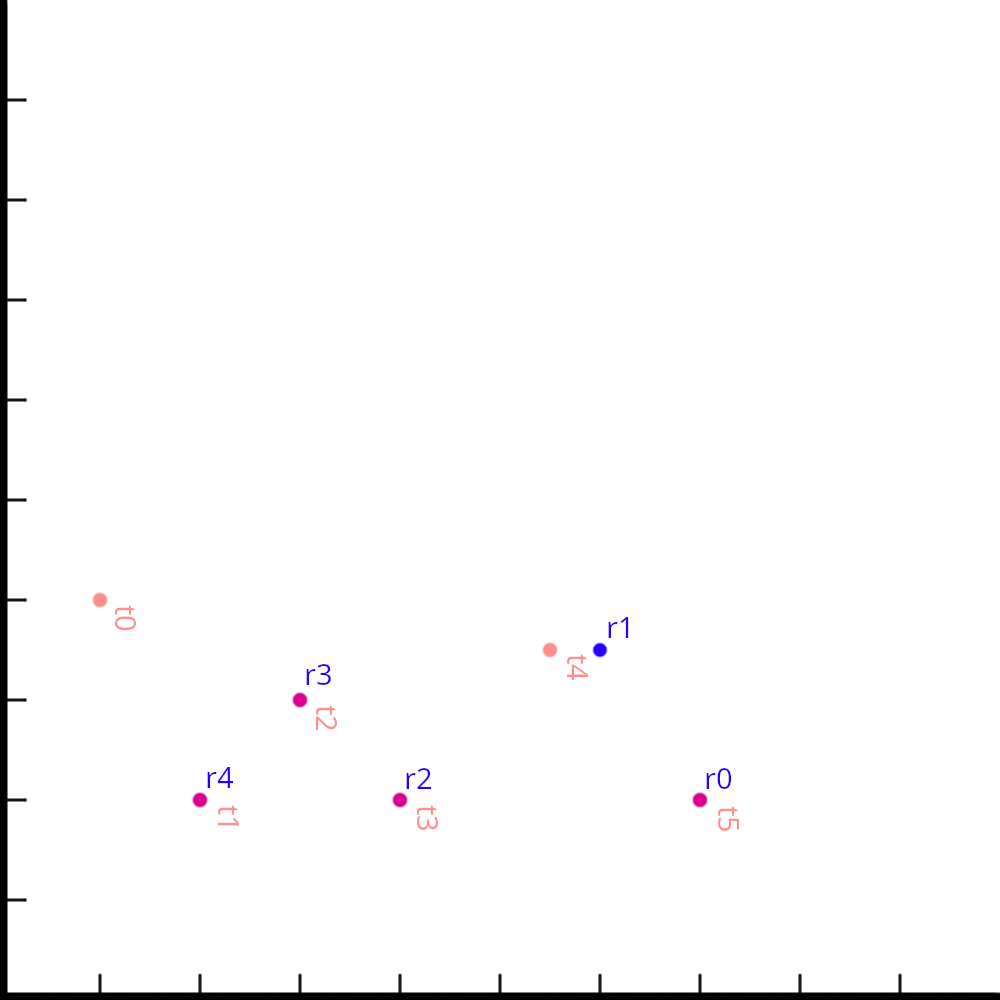
Шаг 2.1. Оптимизация
На этом можно было бы и остановиться, но этот алгоритм не что иное, как грубая сила, он очень медленный. Давайте оценим его сложность. Мы должны перебрать каждую пару звёзд на опорном кадре, это уже квадрат. Также мы должны попробовать совместить её с каждой парой на целевом кадре, это еще квадрат. И после совмещения мы проверяем каждую опорную звезду на совпадение с какой-либо целевой звездой, это еще один квадрат. Итого получаем сложность O(n6). Не очень воодушевляет, правда? Он хорошо и точно находит преобразование, но работает за приемлемое время только для небольшого числа звёзд.
Мы не просто так отсортировали звёзды по яркости на предыдущем шаге. Мы можем взять до 30 (число подобрано опытным путём) самых ярких звёзд с каждого кадра и найти правильное наложение брутфорсом. Если же на снимках больше 30 звёзд, то дальнейшие соответствия будем искать следующим образом.
Берём 31-ю опорную звезду и бежим по всем целевым звёздам, ищем какая из целевых звезд отображается найденным преобразованием с ошибкой меньше допустимой. Не найдя соответствия, отбрасываем опорную звезду. Далее повторяем процесс со следующей опорной звездой. Мы полагаемся на точность преобразования, найденного по небольшому набору звёзд, поэтому теперь нам уже не надо так много проверок. Сложность алгоритма снижается до O(n2), что уже приятнее.
Ищем совпадающие звёзды быстрее
constexpr size_t bruteForceSearchSize = 30;
auto res = BruteForceSearch(bruteForceSearchSize);
...
for (size_t i = bruteForceSearchSize + 1; i < _refStars.size(); ++i)
{
IndexMap temp(res.first);
if (TryRefStar(i, temp, res.second))
return;
}
...
bool TryRefStar(size_t refIndex, IndexMap& matches, const TransformType& transform)
{
if (refIndex == _refStars.size())
{
if (matches.size() > _matches.size() && matches.size() > 2)
{
_matches = matches;
return true;
}
return false;
}
const auto& refStar = _refStars[refIndex];
for (size_t i = 0; i < _targetStars.size(); ++i)
{
auto it = matches.find(i);
if (it != std::end(matches))
continue;
matches.insert({ i, refIndex });
const auto& targetStar = _targetStars[i];
PointF targetPos = targetStar.center;
transform.transform(&targetPos.x, &targetPos.y);
auto penalty = targetPos.Distance(refStar.center);
if (penalty < _eps)
{
if (TryRefStar(refIndex + 1, matches, transform))
return true;
}
matches.erase(i);
}
if (TryRefStar(refIndex + 1, matches, transform))
return true;
return false;
}Шаг 2.2. Широкоугольные проблемы
Если мы фотографируем небольшой участок неба или используем монтировку с ведением, то нам хватит и такого алгоритма. Но если съёмка идет на широкоугольный объектив и с неподвижного штатива, то мы столкнёмся с тем, что звёзды на разных склонениях смещаются по разному. Ярче всего проблема проявляется, если через кадр проходит небесный экватор. Треки звезд из северного и из южного полушарий загибаются в разные стороны, каждые к своему полюсу. Если попытаться наложить кадр просто со сдвигом и поворотом, мы получим примерно следующую картину. Звёзды по краям кадра очень сильно расплывутся.

С этой проблемой можно справиться, если разбить кадры на достаточно малые прямоугольные фрагменты, чтобы разницей в треках звёзд за время съёмки можно было пренебречь. Искать и совмещать звезды будем в каждом фрагменте независимо, дополнительный плюс в том, что это можно делать параллельно. Все найденные соответствия складываются в один общий контейнер.
Ещё немного кода
class AlignmentHelper
{
Stacker& _stacker;
size_t _alignerIndex;
std::mutex _mutex;
AlignmentHelper( Stacker& stacker, size_t alignerIndex )
: _stacker( stacker )
, _alignerIndex( alignerIndex )
{
if ( _stacker._stackingData.size() <= _alignerIndex )
throw std::invalid_argument( "aligner index exceeds tile count" );
}
void Job( uint32_t i )
{
_stacker._aligners[i]->Align( _stacker._stackingData[_alignerIndex].stars[i] );
auto tileMatches = _stacker._aligners[i]->GetMatches();
_mutex.lock();
_stacker._matches.insert( tileMatches.begin(), tileMatches.end() );
_mutex.unlock();
}
public:
static void Run( Stacker& stacker, size_t alignerIndex )
{
AlignmentHelper helper( stacker, alignerIndex );
auto [hTileCount, vTileCount] = GetTileCounts( stacker._width, stacker._height );
oneapi::tbb::parallel_for( oneapi::tbb::blocked_range<int>( 0, hTileCount * vTileCount ), [&helper] ( const oneapi::tbb::blocked_range<int>& range )
{
for ( int i = range.begin(); i < range.end(); ++i )
{
helper.Job( i );
}
} );
}
};Итак, у нас есть список опорных звёзд, список целевых звёзд, а также соответствия между ними. Построим триангуляцию Делоне по целевым звёздам и получим список треугольников. Для триангуляции я использую библиотечный алгоритм, на его деталях мы останавливаться не будем.
Имея список треугольников по целевым звездам и список соответствий между опорными и целевыми звёздами, мы можем сразу построить треугольники и для опорных звёзд. А для каждой пары соответствующих треугольников легко получить аффинное преобразование, отображающее один треугольник в другой.
И ещё немного кода
std::vector<double> coords;
for (auto& match : _matches)
{
coords.push_back(match.first.x);
coords.push_back(match.first.y);
}
delaunator::Delaunator d(coords);
Grid grid;
_grid.clear();
_grid.resize(_gridWidth * _gridHeight);
for (std::size_t i = 0; i < d.triangles.size(); i += 3)
{
Triangle targetTriangle{ PointF {d.coords[2 * d.triangles[i]], d.coords[2 * d.triangles[i] + 1]}, PointF {d.coords[2 * d.triangles[i + 1]], d.coords[2 * d.triangles[i + 1] + 1]}, PointF {d.coords[2 * d.triangles[i + 2]], d.coords[2 * d.triangles[i + 2] + 1]} };
Triangle refTriangle{ _matches[targetTriangle.vertices[0]], _matches[targetTriangle.vertices[1]], _matches[targetTriangle.vertices[2]] };
TriangleTransformPair pair { refTriangle, agg::trans_affine(reinterpret_cast<double*>(refTriangle.vertices.data()), reinterpret_cast<double*>(targetTriangle.vertices.data())) };
for (size_t j = 0; j < _gridWidth * _gridHeight; ++j)
{
RectF cell
{
static_cast<double>((j % _gridWidth) * gridSize),
static_cast<double>((j / _gridWidth) * gridSize),
gridSize,
gridSize
};
if (refTriangle.GetBoundingBox().Overlaps(cell))
{
_grid[j].push_back(pair);
}
}
}Шаг 3. Сложение
Теперь дело за малым: мы можем просто бежать по пикселям опорного кадра, смотреть внутри какого треугольника лежит данный пиксель, отображать координаты в целевую систему соответствующей этому треугольнику матрицей и суммировать сигнал. Ели пиксель находится за пределами любых треугольников, то выбираем ближайший к нему.
Последний фрагмент кода, обещаю
for ( uint32_t x = 0; x < _stacker._width; ++x )
{
PointF p{ static_cast< double >( x ), static_cast< double >( i ) };
size_t hGridIndex = x / _stacker.gridSize;
size_t vGridIndex = i / _stacker.gridSize;
if ( !_stacker._grid.empty() )
{
_stacker.ChooseTriangle( p, lastPair, _stacker._grid[vGridIndex * _stacker._gridWidth + hGridIndex] );
lastPair.second.transform( &p.x, &p.y );
}
if ( ( _stacker._grid.empty() || lastPair.second != agg::trans_affine_null() ) && p.x >= 0 && p.x <= _stacker._width - 1 && p.y >= 0 && p.y <= _stacker._height - 1 )
{
for ( uint32_t ch = 0; ch < channelCount; ++ch )
{
const auto interpolatedChannel = _pBitmap->GetInterpolatedChannel( static_cast< float >( p.x ), static_cast< float >( p.y ), ch );
const size_t index = i * _stacker._width * channelCount + x * channelCount + ch;
auto& mean = _stacker._means[index];
auto& dev = _stacker._devs[index];
auto& n = _stacker._counts[index];
auto sigma = sqrt( dev );
const auto kappa = 3.0;
if ( n <= 5 || fabs( mean - interpolatedChannel ) < kappa * sigma )
{
dev = n * ( dev + ( interpolatedChannel - mean ) * ( interpolatedChannel - mean ) / ( n + 1 ) ) / ( n + 1 );
mean = std::clamp( ( n * mean + interpolatedChannel ) / ( n + 1 ), 0.0f, static_cast< float >( std::numeric_limits<typename PixelFormatTraits<pixelFormat>::ChannelType>::max() ) );
++n;
}
}
}
}Заключение
Целиком проект доступен на моём гитхабе. Хотя он ещё находится на ранней стадии разработки, я уже использую его для обработки своих астрофотографий, и результаты вполне способны радовать глаз. Один из таких результатов на КПДВ, еще несколько под спойлером.
Несколько примеров фотографий




Если сообществу будет интересно, то в следующей статье расскажу подробнее о внутреннем устройстве проекта и приведу сравнение с аналогами по качеству и по производительности.
Автор: Алексей Коксин






