Совсем недавно мне пришлось решать очередную тривиальную учебную задачу от своего преподавателя. Однако, решая ее, мне удалось обратить внимание на вещи о коих я ранее вовсе не задумывался, возможно, не задумывались и Вы. Эта статья скорее будет полезна студентам да и всем, кто начинает свой путь в мир параллельного программирования с использованием MPI.

Наше «Дано: »
Итак, суть нашей, в сущности вычислительной задачи, заключается в том, чтобы сравнить во сколько раз программа, использующая неблокирующие отложенные двухточечные передачи быстрее той, что использует блокирующие двухточечные передачи. Измерения будем проводить для входных массивов размерностью 64, 256, 1024, 4096, 8192, 16384, 65536, 262144, 1048576, 4194304, 16777216, 33554432 элементов. По умолчанию предлагается решать ее четырьмя процессами. А вот, собственно, и то, что мы будем считать:
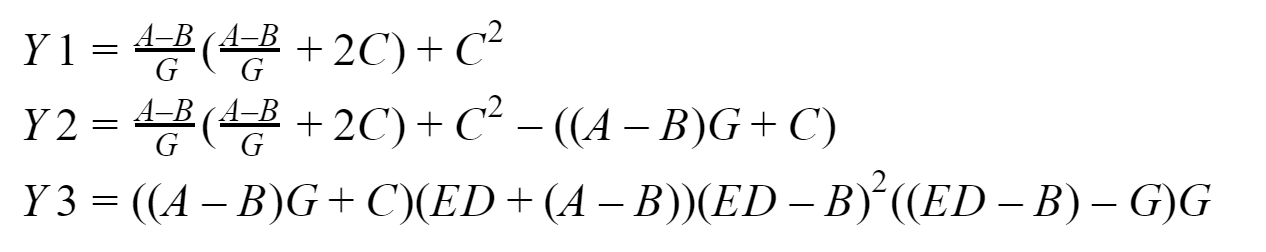
На выходе у нас должно получиться три вектора: Y1, Y2 и Y3, которые соберет у себя нулевой процесс. Все это дело я буду тестировать на своей системе на базе процессора Intel с 16 ГБ ОЗУ. Для разработки программ будем использовать реализацию стандарта MPI от Microsoft версии 9.0.1 (на момент написания статьи она актуальна), Visual Studio Community 2017 и не Fortran.
Матчасть
Я бы не хотел подробно описывать то, как работают функции MPI, которые будут использованы, за этим всегда можно сходить и подсмотреть в документацию, поэтому проведу лишь краткий обзор того, что мы будем использовать.
Блокирующий обмен
Для блокирующего обмена сообщениями типа точка-точка будем пользоваться функциями:
MPI_Send — осуществляет блокирующую отправку сообщения, т.е. после вызова функции процесс блокируется до тех пор пока отправляемые им данные не будут записаны из его памяти в внутрисистемный буфер среды MPI, после процесс продолжает работать дальше;
MPI_Recv — осуществляет блокирующий прием сообщения, т.е. после вызова функции процесс блокируется до тех пор пока не поступят данные от процесса-отправителя и пока эти данные не будут полностью записаны в буфер процесса-приемника средой MPI.
Отложенный неблокирующий обмен
Для отложенного неблокирующего обмена сообщениями типа точка-точка будем пользоваться функциями:
MPI_Send_init — в фоновом режиме подготавливает среду к посылке данных, которая произойдет в некотором будущем и никаких блокировок;
MPI_Recv_init — эта функция работает аналогично предыдущей, только на этот раз для приема данных;
MPI_Start — запускает сам процесс приема или передачи сообщения, он так же проходит в фоновом режиме а.к.а. без блокировки;
MPI_Wait — используется для проверки и, при необходимости, ожидания завершения посылки или приема сообщения, а вот она как раз и блочит процесс при необходимости (если данные «недоотправлены» или «недоприняты»). Например, процесс хочет использовать данные, которые к нему еще не дошли — не хорошо, поэтому вставляем MPI_Wait перед тем местом, где ему эти данные понадобятся (вставляем её даже если просто есть риск повреждения данных). Еще пример, процесс запустил фоновую передачу данных, а после запуска передачи данных сразу же стал эти данные как-то изменять — не хорошо, поэтому вставляем MPI_Wait перед тем местом в программе, где он начинает эти данные изменять (тут так же вставляем её даже если просто есть риск повреждения данных).
Таким образом семантически последовательность вызовов при отложенном неблокирующем обмене такая:
- MPI_Send_init / MPI_Recv_init — готовим среду к приему или передаче
- MPI_Start — запускаем процесс приема/передачи
- MPI_Wait — вызываем при риске повреждения (в т.ч. «недоотправки» и «недоприема») передаваемых или принимаемых данных
Так же я использовал в своих тестовых программах MPI_Startall, MPI_Waitall, смысл их в принципе аналогичен MPI_Start и MPI_Wait соответственно, только они оперируют несколькими посылками и/или передачами. Но это еще далеко не весь список функций старта и ожидания, есть еще несколько функций проверки завершенности операций.
Архитектура связей между процессами
Для наглядности построим граф выполнения вычислений четырьмя процессами. При этом надо постараться относительно равномерно распределить все векторные арифметические операции по процессам. Вот что у меня получилось:
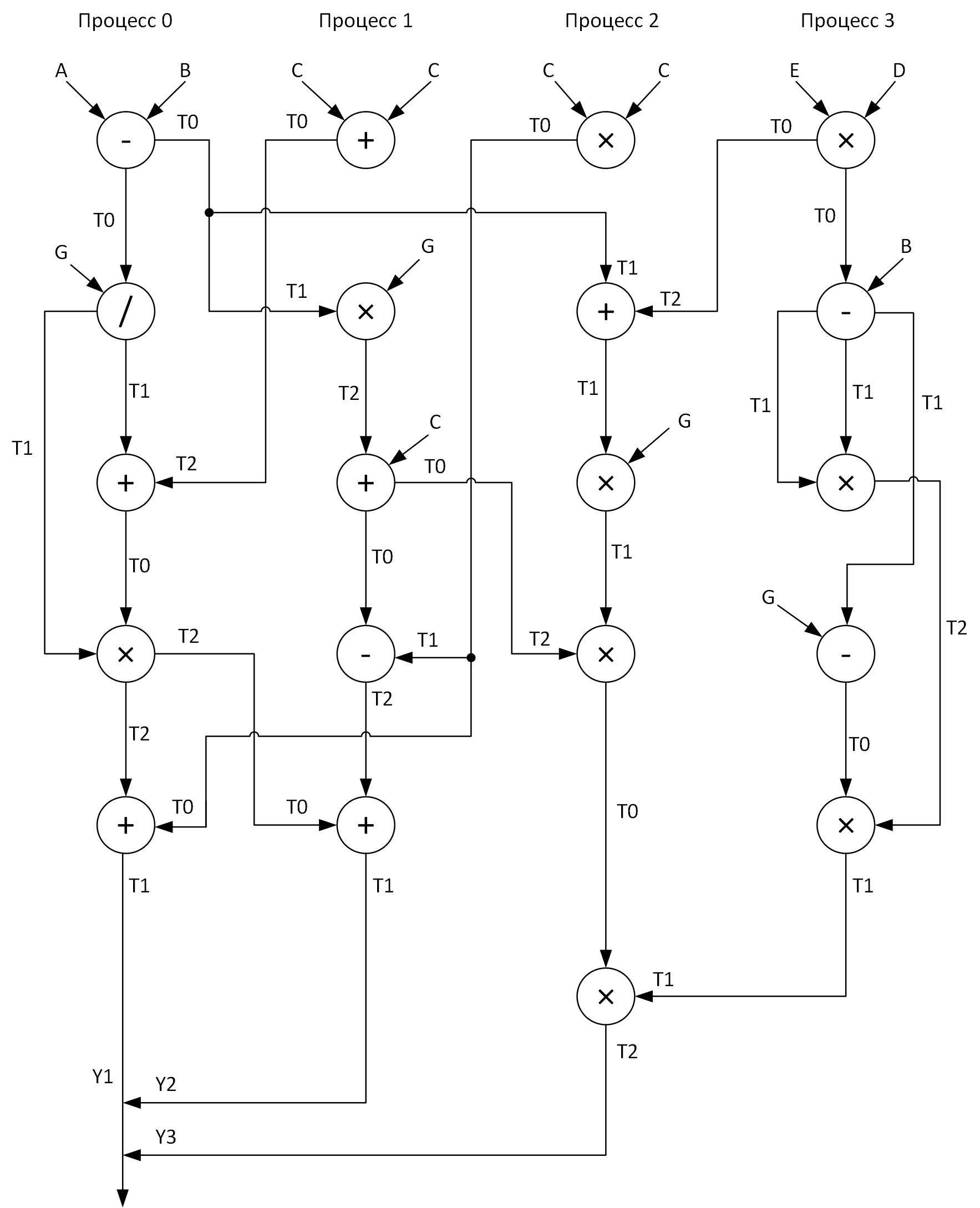
Видите эти массивы T0-T2? Это буферы для хранения промежуточных результатов операций. Так же на графе при передаче сообщений от одного процесса к другому в начале стрелки стоит название массива, данные которого передаются, а в конце стрелки — массив, принимающий эти данные.
Ну что же, когда мы наконец ответили на вопросы:
- Что за задачу решаем?
- Какие средства будем использовать для ее решения?
- Как будем ее решать?
Осталось только ее решить…
Наше «Решение: »
Далее я представлю коды двух программ о которых шла речь выше, но для начала дам еще немного пояснений что да как.
Все векторные арифметические операции я вынес в отдельные процедуры (add, sub, mul, div) дабы увеличить читаемость кода. Все входные массивы инициализируются в соответствии с формулами, которые я указал почти что наобум. Так как нулевой процесс осуществляет сборку результатов работы со всех остальных процессов, следовательно, он работает дольше всех, поэтому время его работы логично считать равным времени выполнения программы (как мы помним, нас интересует: арифметика + меседжинг) и в первом и во втором случае. Измерение интервалов времени будем осуществлять с помощью функции MPI_Wtime и заодно я решил вывести какое у меня там разрешение часиков с помощью MPI_Wtick (где-то в душе я надеюсь, что они подвяжутся к моему инвариантному TSC, в этом случае, я даже готов простить им погрешность, связанную с временем вызова функции MPI_Wtime). Так вот, соберем воедино все о чем я писал выше и в соответствии с графом разработаем наконец эти программы (и отладим конечно же тоже).
Кому интересно посмотреть код:
#include "pch.h"
#include <iostream>
#include <iomanip>
#include <fstream>
#include <mpi.h>
using namespace std;
void add(double *A, double *B, double *C, int n);
void sub(double *A, double *B, double *C, int n);
void mul(double *A, double *B, double *C, int n);
void div(double *A, double *B, double *C, int n);
int main(int argc, char **argv)
{
if (argc < 2)
{
return 1;
}
int n = atoi(argv[1]);
int rank;
double start_time, end_time;
MPI_Status status;
double *A = new double[n];
double *B = new double[n];
double *C = new double[n];
double *D = new double[n];
double *E = new double[n];
double *G = new double[n];
double *T0 = new double[n];
double *T1 = new double[n];
double *T2 = new double[n];
for (int i = 0; i < n; i++)
{
A[i] = double (2 * i + 1);
B[i] = double(2 * i);
C[i] = double(0.003 * (i + 1));
D[i] = A[i] * 0.001;
E[i] = B[i];
G[i] = C[i];
}
cout.setf(ios::fixed);
cout << fixed << setprecision(9);
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
if (rank == 0)
{
start_time = MPI_Wtime();
sub(A, B, T0, n);
MPI_Send(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD);
MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD);
div(T0, G, T1, n);
MPI_Recv(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status);
add(T1, T2, T0, n);
mul(T0, T1, T2, n);
MPI_Recv(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status);
MPI_Send(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD);
add(T0, T2, T1, n);
MPI_Recv(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status);
MPI_Recv(T2, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status);
end_time = MPI_Wtime();
cout << "Clock resolution: " << MPI_Wtick() << " secs" << endl;
cout << "Thread " << rank << " execution time: " << end_time - start_time << endl;
}
if (rank == 1)
{
add(C, C, T0, n);
MPI_Recv(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status);
MPI_Send(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
mul(T1, G, T2, n);
add(T2, C, T0, n);
MPI_Recv(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &status);
MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD);
sub(T1, T0, T2, n);
MPI_Recv(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status);
add(T0, T2, T1, n);
MPI_Send(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
}
if (rank == 2)
{
mul(C, C, T0, n);
MPI_Recv(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &status);
MPI_Recv(T2, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &status);
MPI_Send(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD);
MPI_Send(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
add(T1, T2, T0, n);
mul(T0, G, T1, n);
MPI_Recv(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &status);
mul(T1, T2, T0, n);
MPI_Recv(T1, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &status);
mul(T0, T1, T2, n);
MPI_Send(T2, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD);
}
if (rank == 3)
{
mul(E, D, T0, n);
MPI_Send(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD);
sub(T0, B, T1, n);
mul(T1, T1, T2, n);
sub(T1, G, T0, n);
mul(T0, T2, T1, n);
MPI_Send(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD);
}
MPI_Finalize();
delete[] A, B, C, D, E, G, T0, T1, T2;
return 0;
}
void add(double *A, double *B, double *C, int n)
{
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] + B[i];
}
}
void sub(double *A, double *B, double *C, int n)
{
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] - B[i];
}
}
void mul(double *A, double *B, double *C, int n)
{
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] * B[i];
}
}
void div(double *A, double *B, double *C, int n)
{
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] / B[i];
}
}
#include "pch.h"
#include <iostream>
#include <iomanip>
#include <fstream>
#include <mpi.h>
using namespace std;
void add(double *A, double *B, double *C, int n);
void sub(double *A, double *B, double *C, int n);
void mul(double *A, double *B, double *C, int n);
void div(double *A, double *B, double *C, int n);
int main(int argc, char **argv)
{
if (argc < 2)
{
return 1;
}
int n = atoi(argv[1]);
int rank;
double start_time, end_time;
MPI_Request request[7];
MPI_Status statuses[4];
double *A = new double[n];
double *B = new double[n];
double *C = new double[n];
double *D = new double[n];
double *E = new double[n];
double *G = new double[n];
double *T0 = new double[n];
double *T1 = new double[n];
double *T2 = new double[n];
for (int i = 0; i < n; i++)
{
A[i] = double(2 * i + 1);
B[i] = double(2 * i);
C[i] = double(0.003 * (i + 1));
D[i] = A[i] * 0.001;
E[i] = B[i];
G[i] = C[i];
}
cout.setf(ios::fixed);
cout << fixed << setprecision(9);
MPI_Init(&argc, &argv);
MPI_Comm_rank(MPI_COMM_WORLD, &rank);
if (rank == 0)
{
start_time = MPI_Wtime();
MPI_Send_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[0]);//
MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[1]);//
MPI_Recv_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[2]);//
MPI_Recv_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[3]);//
MPI_Send_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[4]);//
MPI_Recv_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[5]);//
MPI_Recv_init(T2, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[6]);//
MPI_Start(&request[2]);
sub(A, B, T0, n);
MPI_Startall(2, &request[0]);
div(T0, G, T1, n);
MPI_Waitall(3, &request[0], statuses);
add(T1, T2, T0, n);
mul(T0, T1, T2, n);
MPI_Startall(2, &request[3]);
MPI_Wait(&request[3], &statuses[0]);
add(T0, T2, T1, n);
MPI_Startall(2, &request[5]);
MPI_Wait(&request[4], &statuses[0]);
MPI_Waitall(2, &request[5], statuses);
end_time = MPI_Wtime();
cout << "Clock resolution: " << MPI_Wtick() << " secs" << endl;
cout << "Thread " << rank << " execution time: " << end_time - start_time << endl;
}
if (rank == 1)
{
MPI_Recv_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[0]);//
MPI_Send_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[1]);//
MPI_Recv_init(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[2]);//
MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[3]);//
MPI_Recv_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[4]);//
MPI_Send_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[5]);//
MPI_Start(&request[0]);
add(C, C, T0, n);
MPI_Start(&request[1]);
MPI_Wait(&request[0], &statuses[0]);
mul(T1, G, T2, n);
MPI_Start(&request[2]);
MPI_Wait(&request[1], &statuses[0]);
add(T2, C, T0, n);
MPI_Start(&request[3]);
MPI_Wait(&request[2], &statuses[0]);
sub(T1, T0, T2, n);
MPI_Wait(&request[3], &statuses[0]);
MPI_Start(&request[4]);
MPI_Wait(&request[4], &statuses[0]);
add(T0, T2, T1, n);
MPI_Start(&request[5]);
MPI_Wait(&request[5], &statuses[0]);
}
if (rank == 2)
{
MPI_Recv_init(T1, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[0]);//
MPI_Recv_init(T2, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &request[1]);//
MPI_Send_init(T0, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[2]);//
MPI_Send_init(T0, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[3]);//
MPI_Recv_init(T2, n, MPI_DOUBLE, 1, 0, MPI_COMM_WORLD, &request[4]);//
MPI_Recv_init(T1, n, MPI_DOUBLE, 3, 0, MPI_COMM_WORLD, &request[5]);//
MPI_Send_init(T2, n, MPI_DOUBLE, 0, 0, MPI_COMM_WORLD, &request[6]);//
MPI_Startall(2, &request[0]);
mul(C, C, T0, n);
MPI_Startall(2, &request[2]);
MPI_Waitall(4, &request[0], statuses);
add(T1, T2, T0, n);
MPI_Start(&request[4]);
mul(T0, G, T1, n);
MPI_Wait(&request[4], &statuses[0]);
mul(T1, T2, T0, n);
MPI_Start(&request[5]);
MPI_Wait(&request[5], &statuses[0]);
mul(T0, T1, T2, n);
MPI_Start(&request[6]);
MPI_Wait(&request[6], &statuses[0]);
}
if (rank == 3)
{
MPI_Send_init(T0, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[0]);
MPI_Send_init(T1, n, MPI_DOUBLE, 2, 0, MPI_COMM_WORLD, &request[1]);
mul(E, D, T0, n);
MPI_Start(&request[0]);
sub(T0, B, T1, n);
mul(T1, T1, T2, n);
MPI_Wait(&request[0], &statuses[0]);
sub(T1, G, T0, n);
mul(T0, T2, T1, n);
MPI_Start(&request[1]);
MPI_Wait(&request[1], &statuses[0]);
}
MPI_Finalize();
delete[] A, B, C, D, E, G, T0, T1, T2;
return 0;
}
void add(double *A, double *B, double *C, int n)
{
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] + B[i];
}
}
void sub(double *A, double *B, double *C, int n)
{
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] - B[i];
}
}
void mul(double *A, double *B, double *C, int n)
{
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] * B[i];
}
}
void div(double *A, double *B, double *C, int n)
{
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] / B[i];
}
}
Тестирование и анализ
Давайте запустим наши программы для массивов разных размеров и посмотрим что из этого выйдет. Результаты тестов сведем в таблицу, в последнем столбце которой рассчитаем и запишем коэффициент ускорения, который определим так: Куск = Tотл. неблок. / Tблок.
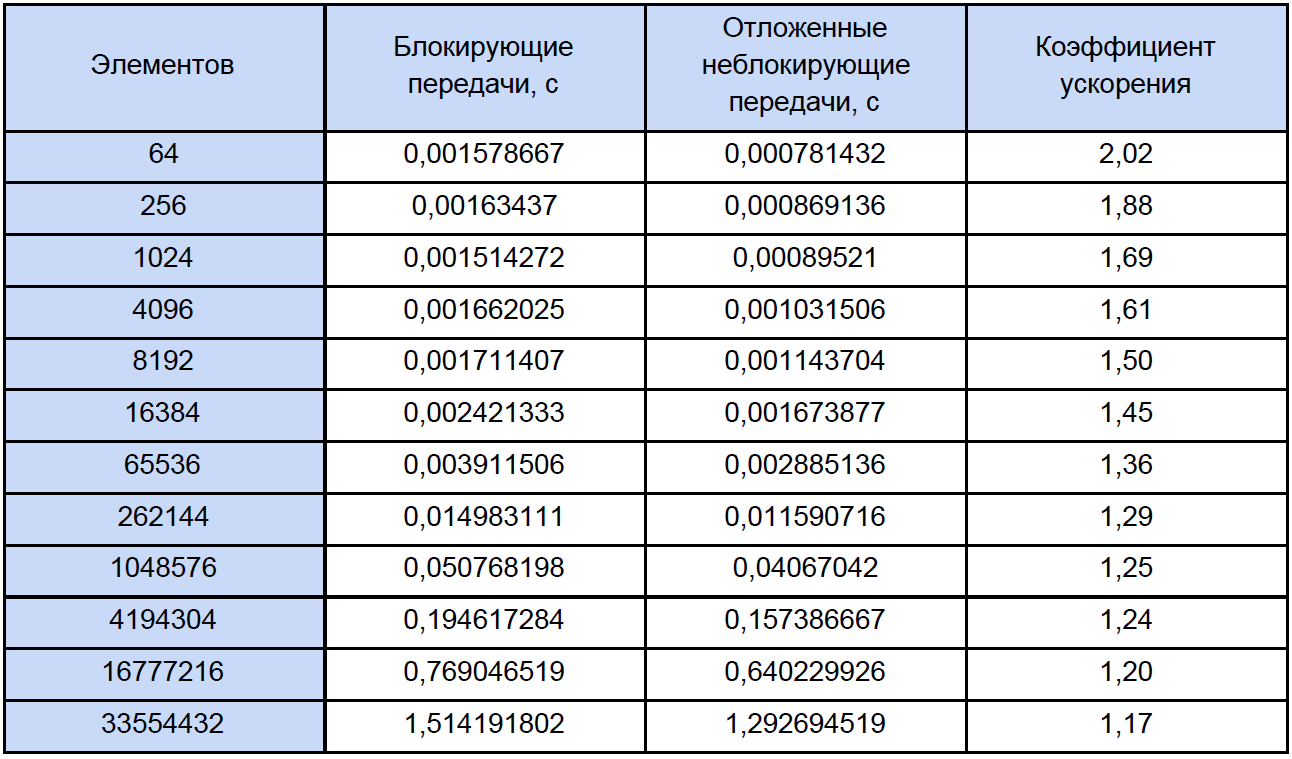
Если посмотреть на эту таблицу чуть внимательнее чем обычно, то можно заметить, что при увеличении числа обрабатываемых элементов коэффициент ускорения убывает как-то так:
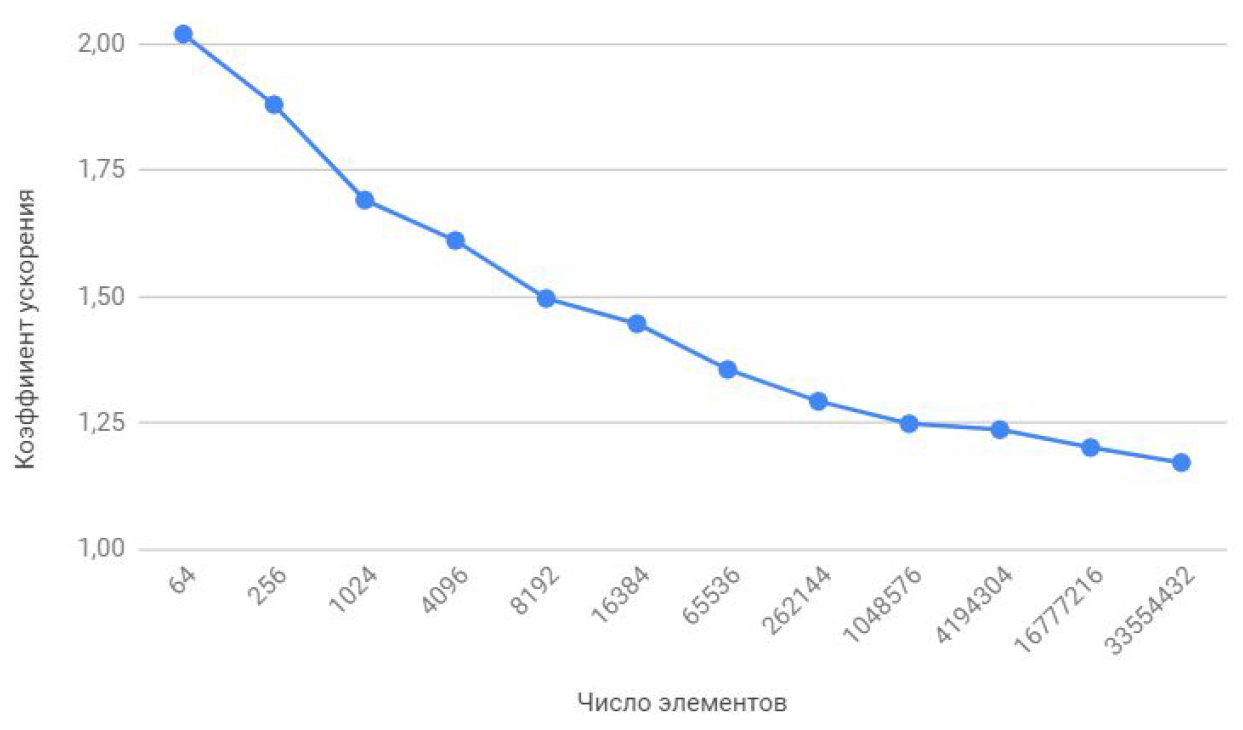
Давайте попробуем определить в чем же дело? Для этого я предлагаю написать маленькую тестовую программку, которая будет измерять время каждой векторной арифметической операции и бережно сводить результаты в обыкновенный текстовый файл.
Вот, собственно, сама программа:
#include "pch.h"
#include <iostream>
#include <iomanip>
#include <Windows.h>
#include <fstream>
using namespace std;
void add(double *A, double *B, double *C, int n);
void sub(double *A, double *B, double *C, int n);
void mul(double *A, double *B, double *C, int n);
void div(double *A, double *B, double *C, int n);
int main()
{
struct res
{
double add;
double sub;
double mul;
double div;
};
int i, j, k, n, loop;
LARGE_INTEGER start_time, end_time, freq;
ofstream fout("test_measuring.txt");
int N[12] = { 64, 256, 1024, 4096, 8192, 16384, 65536, 262144, 1048576, 4194304, 16777216, 33554432 };
SetConsoleOutputCP(1251);
cout << "Введите число циклов loop: ";
cin >> loop;
fout << setiosflags(ios::fixed) << setiosflags(ios::right) << setprecision(9);
fout << "Циклов измерений: " << loop << endl;
fout << setw(10) << "n Элементов" << setw(30) << "Ср. время суммирования (c)" << setw(30) << "Ср. время вычитания (c)"
<< setw(30) << "Ср.время умножения (c)" << setw(30) << "Ср. время деления (c)" << endl;
QueryPerformanceFrequency(&freq);
cout << "nЧастота счета: " << freq.QuadPart << " Гц" << endl;
for (k = 0; k < sizeof(N) / sizeof(int); k++)
{
res output = {};
n = N[k];
double *A = new double[n];
double *B = new double[n];
double *C = new double[n];
for (i = 0; i < n; i++)
{
A[i] = 2.0 * i;
B[i] = 2.0 * i + 1;
C[i] = 0;
}
for (j = 0; j < loop; j++)
{
QueryPerformanceCounter(&start_time);
add(A, B, C, n);
QueryPerformanceCounter(&end_time);
output.add += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart);
QueryPerformanceCounter(&start_time);
sub(A, B, C, n);
QueryPerformanceCounter(&end_time);
output.sub += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart);
QueryPerformanceCounter(&start_time);
mul(A, B, C, n);
QueryPerformanceCounter(&end_time);
output.mul += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart);
QueryPerformanceCounter(&start_time);
div(A, B, C, n);
QueryPerformanceCounter(&end_time);
output.div += double(end_time.QuadPart - start_time.QuadPart) / double(freq.QuadPart);
}
fout << setw(10) << n << setw(30) << output.add / loop << setw(30) << output.sub / loop
<< setw(30) << output.mul / loop << setw(30) << output.div / loop << endl;
delete[] A, B, C;
}
fout.close();
cout << endl;
system("pause");
return 0;
}
void add(double *A, double *B, double *C, int n)
{
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] + B[i];
}
}
void sub(double *A, double *B, double *C, int n)
{
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] - B[i];
}
}
void mul(double *A, double *B, double *C, int n)
{
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] * B[i];
}
}
void div(double *A, double *B, double *C, int n)
{
for (size_t i = 0; i < n; i++)
{
C[i] = A[i] / B[i];
}
}
При запуске она просит ввести число циклов измерений, я тестировал для 10000 циклов. На выходе получаем усредненный результат по каждой операции:
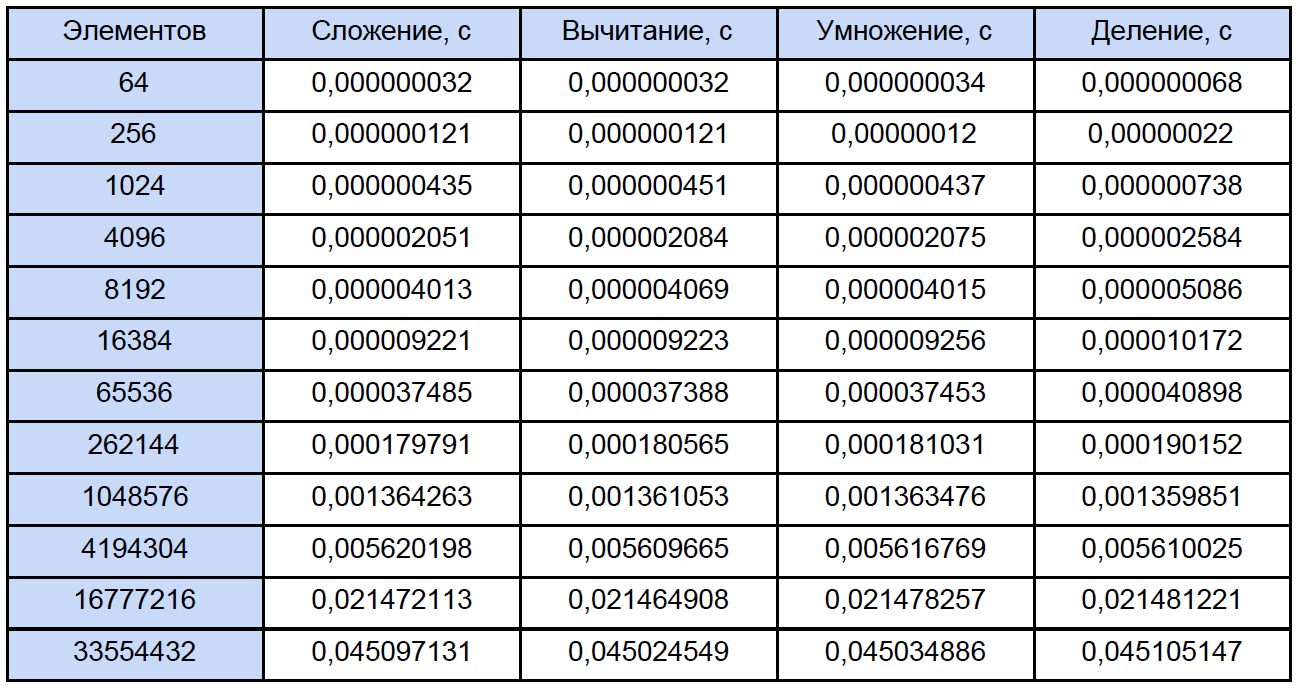
Для измерения времени я использовал высокоуровненую QueryPerformanceCounter. Настойчиво рекомендую почитать этот FAQ чтобы большинство вопросов по измерению времени этой функцией отпали сами собой. Она по моим наблюдениям цепляется за TSC (но теоретически может и не за него), а возвращает, согласно справке, текущее число тиков счетчика. Но дело в том, что мой счетчик физически не может измерить интервал времени 32 нс (см. первую строку таблицы результатов). Такой результат получается из-за того, что между двумя вызовами QueryPerformanceCounter проходит то 0 тиков, то 1. Для первой строки в таблице можно лишь заключить, что примерно треть результатов из 10000 равны 1 тик. Так что данные в этой таблице для 64, 256 и даже для 1024 элементов есть нечто совсем приблизительное. Теперь, давайте откроем любую из программ и посчитаем сколько всего операций каждого типа в ней встречается, традиционно все «размажем» по очередной таблице:
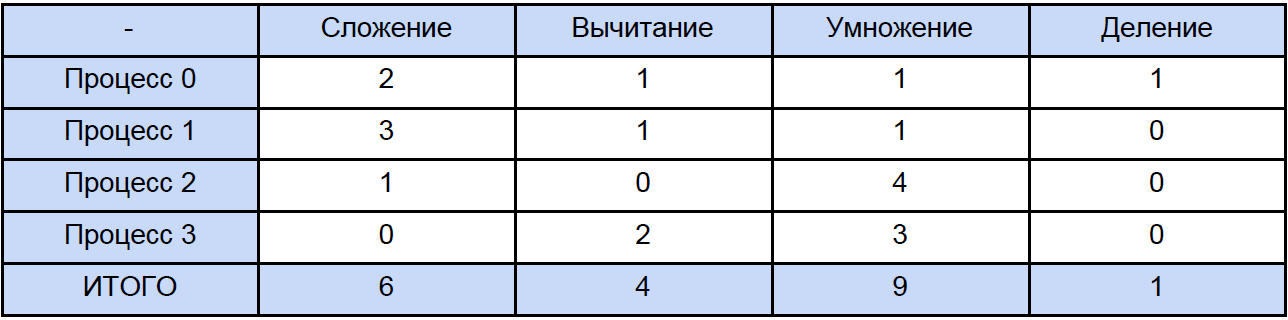
Наконец-то мы знаем время каждой векторной арифметической операции и сколько её в нашей программе, попробуем узнать сколько времени тратится на эти операции в параллельных программах и сколько времени уходит на блокирующий и отложенный неблокирующий обмен данными между процессами и снова, для наглядности, сведем это в таблицу:
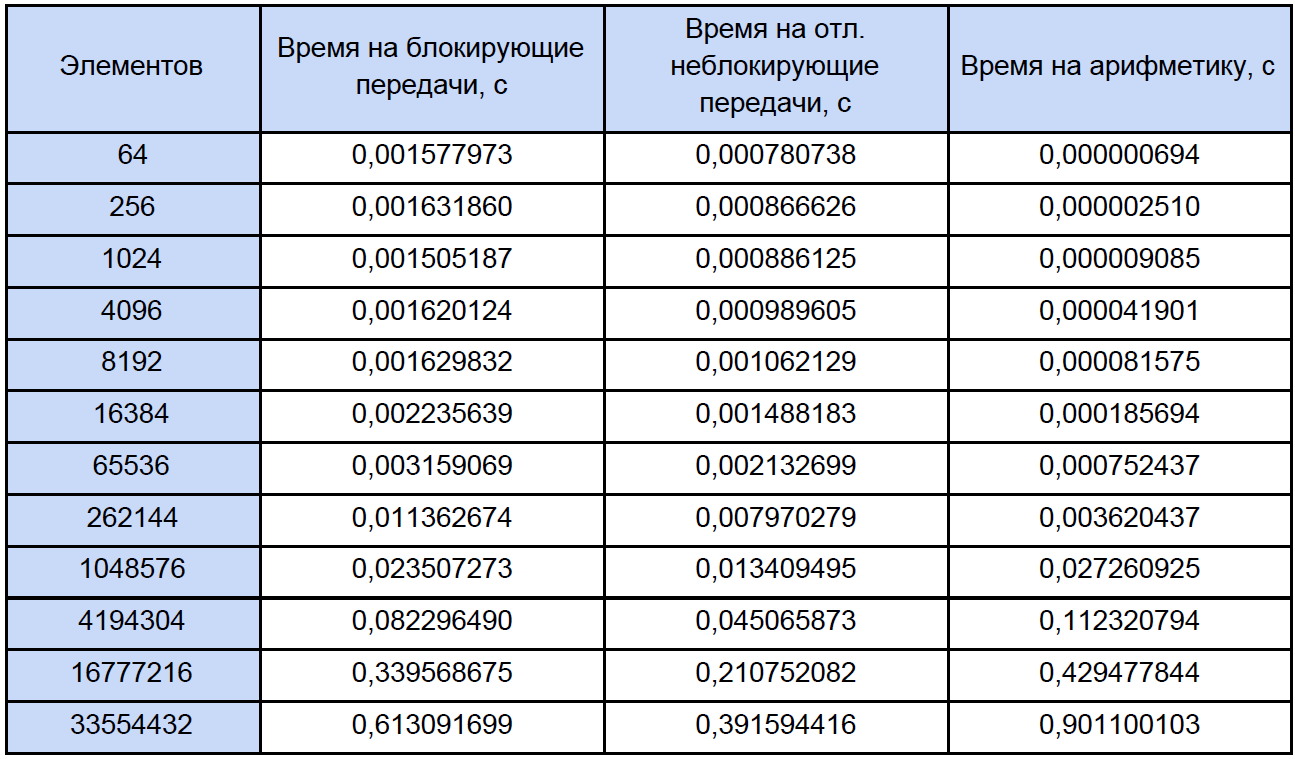
По результатам полученных данных построим график трех функций: первая — описывает изменение времени, тратящегося на блокирующие передачи между процессами, от числа элементов массивов, вторая — изменение времени, тратящегося на отложенные неблокирующие передачи между процессами, от числа элементов массивов и третья — изменение времени, тратящегося на арифметические операции, от числа элементов массивов:
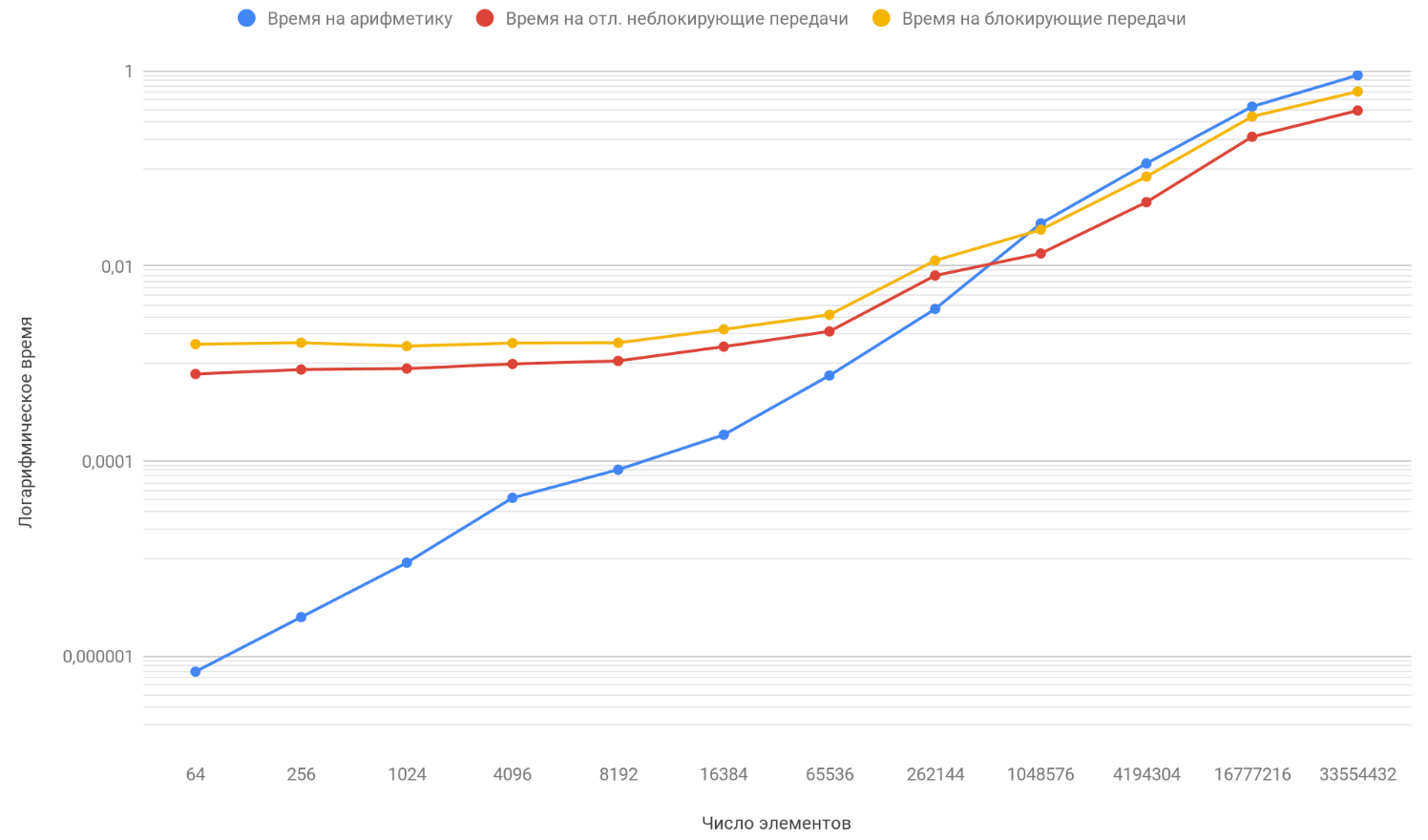
Как вы уже обратили внимание, вертикальная шкала графика — логарифмическая, это вынужденная мера, т.к. разброс времен слишком большой и на обычном графике не было бы видно ровным счетом ничего. Обратите внимание на функцию зависимости времени, затрачиваемого на арифметику, от количества элементов, она благополучно обгоняет две другие функции уже на приблизительно на 1 млн. элементов. Все дело в том, что она растет на бесконечности быстрее, чем два ее оппонента. Поэтому, с увеличением числа обрабатываемых элементов, время работы программ все более определяется арифметикой, а не передачами. Предположим, что вы увеличили число передач между процессами, концептуально вы увидите лишь то, что момент, когда функция арифметики обгонит две другие произойдет попозже.
Итоги
Таким образом, продолжая увеличивать длину массивов вы придете к тому, что программа с отложенными неблокирующими передачами будет лишь совсем немного быстрее той, что использует блокирующий обмен. А если устремить длину массивов в бесконечность (ну или просто брать очень уж длинные массивы), то время работы вашей программы будет прочти на 100% определяться вычислениями, а коэффициент ускорения будет благополучно стремиться к 1.
Автор: cotterrium






