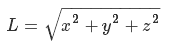Трудно поспорить, что ландшафт — неотъемлемая часть большинства компьютерных игр на открытых пространствах. Традиционный метод реализации изменения рельефа окружающей игрока поверхности следующий — берем сетку (Mesh), представляющую из себя плоскость и для каждого примитива в этой сетке производим смещение по нормали к этой плоскости на значение, конкретное для данного примитива. Говоря простыми словами, у нас есть одноканальная текстура размером 256 на 256 пикселей и сетка плоскости. Для каждого примитива по его координатам на плоскости берем значение из текстуры. Теперь просто смещаем по нормали к плоскости координаты примитива на полученное значение(рис.1)
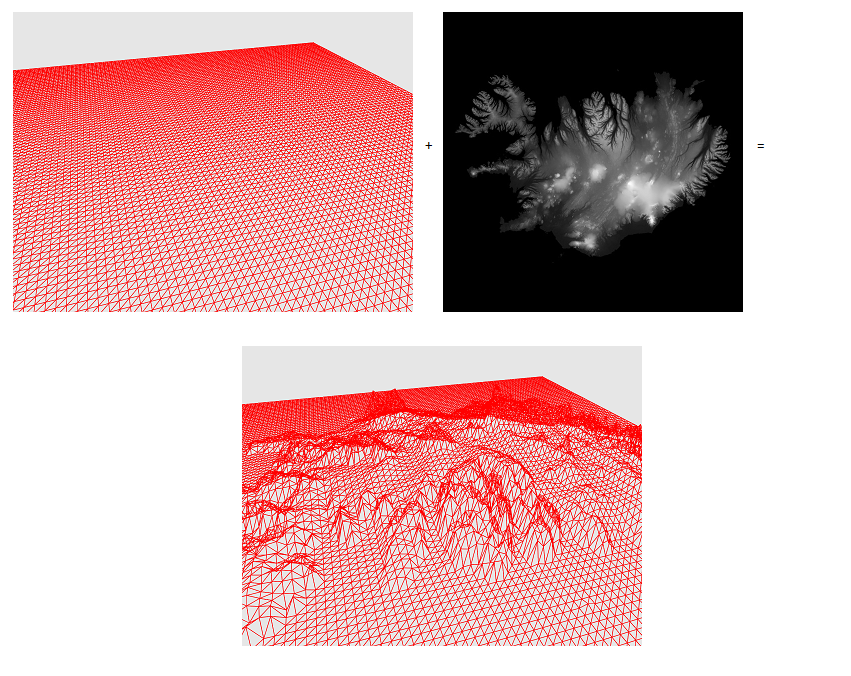
Рис.1 карта высот + плоскость = ландшафт
Почему это работает? Если представить, что игрок находится на поверхности сферы, и радиус этой сферы чрезвычайно велик по отношению к размеру игрока, то искривлением поверхности можно пренебречь и использовать плоскость. Но что если не пренебрегать тем фактом, что мы находимся на сфере? Своим опытом построения такого рода ландшафтов я хочу поделиться с читателем в данной статье.
1. Сектор
Очевидно, что не разумно строить ландшафт сразу для всей сферы — большую ее часть не будет видно. Поэтому нам нужно создать некую минимальную область пространства — некий примитив, из которых будет состоять рельеф видимой части сферы. Я назову его сектор. Как же нам его получить? Итак, посмотрите на рис.2a. Зеленая ячейка — это наш сектор. Далее построим шесть сеток, каждая из которых является гранью куба (рис.2b). Теперь давайте нормализуем координаты примитивов, которые формируют сетки (рис.2с).
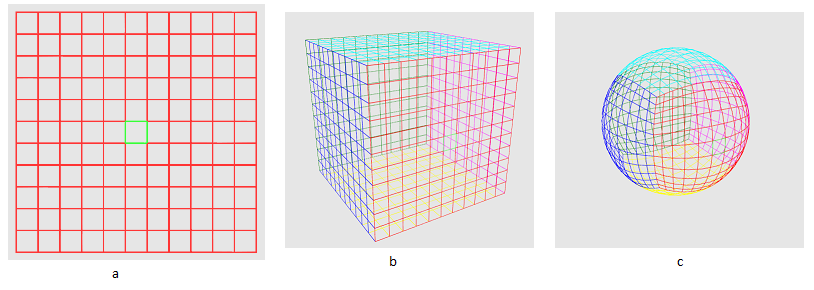
Рис.2
В итоге мы получили спроецированный на сферу куб, где сектором является область на одной из его граней. Почему это работает? Рассмотрим произвольную точку на сетке как вектор от начала координат. Что есть нормализация вектора? Это преобразование заданного вектора в вектор в том же направлении, но с единичной длиной. Процесс следующий: сперва найдем длину вектора в евклидовой метрике согласно теореме Пифагора
Затем поделим каждый из компонентов вектора на это значение
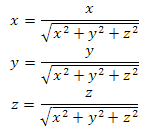
Теперь спросим себя, что такое сфера? Сфера — это множество точек, равноудаленных от заданной точки. Параметрическое уравнение сферы выглядит так
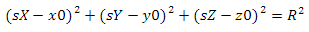
где x0, y0, z0 — координаты центра сферы, а R — ее радиус. В нашем случае центр сферы — это начало координат, а радиус равен единице. Подставляем известные значения и берем корень от двух частей уравнения. Получается следующее
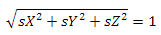
Буквально последнее преобразование говорит нам следующее: «Для того, чтобы принадлежать сфере, длина вектора должна быть равна единице». Этого мы и добились нормализацией.
А что если сфера имеет произвольный центр и радиус? Найти точку, которая ей принадлежит, можно с помощью следующего уравнения
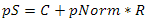
где pS — точка на сфере, C — центр сферы, pNorm — ранее нормализованный вектор и R — радиус сферы. Говоря простыми словами, здесь происходит следующее — «мы перемещаемся от центра сферы по направлению к точке на сетке на расстояние R». Так как каждый вектор имеет единичную длину, то в итоге все точки равноудалены от центра сферы на расстояние ее радиуса, что делает истинным уравнение сферы.
2. Управление
Нам нужно получить группу секторов, которые потенциально видны из точки обзора. Но как это сделать? Предположим, что у нас есть сфера с центром в некоторой точке. Также у нас есть сектор, который расположен на сфере и точка P, расположенная в пространстве около сферы. Теперь построим два вектора — один направлен от центра сферы до центра сектора, другой — от центра сферы до точки обзора. Посмотрите на рис.3 — сектор может быть виден только если абсолютное значение угла между этими векторами меньше 90 градусов.
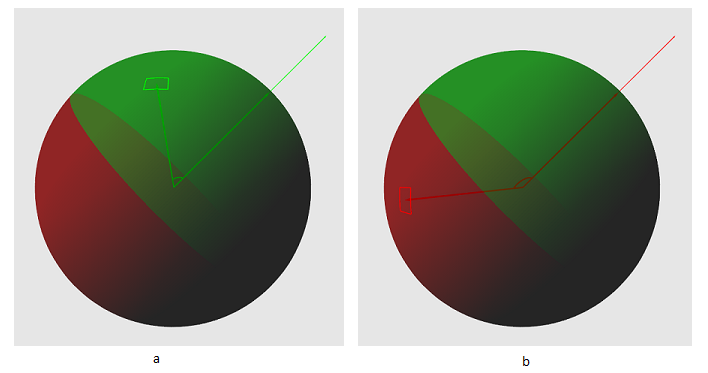
Рис.3 a — угол меньше 90 — сектор потенциально виден. b — угол болше 90 — сектор не виден
Как получить этот угол? Для этого нужно использовать скалярное произведение векторов. Для трехмерного случая оно вычисляется так:
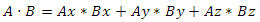
Скалярное произведение обладает дистрибутивным свойством:
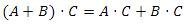
Ранее мы определили уравнение длины вектора — теперь мы можем сказать, что длина вектора равна корню от скалярного произведения этого вектора самого на себя. Или наоборот — скалярное произведения вектора самого на себя равно квадрату его длины.
Теперь давайте обратимся к закону косинусов. Одна из двух его формулировок выглядит так(рис.4):
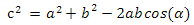
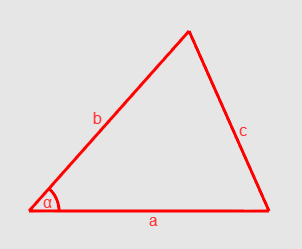
Рис.4 закон косинусов
Если взять за a и b длины наших векторов, тогда угол alfa — то, что мы ищем. Но как нам получить значение с? Смотрите: если мы отнимем a от b, то получим вектор, направленный от a к b, а так как вектор характеризуется лишь направлением и длиной, то мы можем графически расположить его начало в конце вектора a. Исходя из этого, мы можем сказать, что с равен длине вектора b — a. Итак, у нас получилось
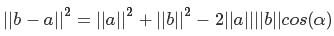
выразим квадраты длин как скалярные произведения
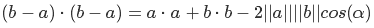
раскроем скобки, пользуясь дистрибутивным свойством
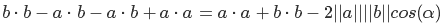
немного сократим
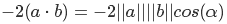
и наконец, поделив обе чести уравнения на минус два, получим
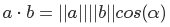
Это еще одно свойство скалярного произведения. В нашем случае надо нормализовать векторы, чтобы их длины были равны единице. Угол нам вычислять не обязательно — достаточно значения косинуса. Если оно меньше нуля — то можно смело утверждать, что этот сектор нас не интересует
3. Сетка
Пора задуматься о том, как рисовать примитивы. Как я говорил ранее, сектор является основным компонентом в нашей схеме, поэтому для каждого потенциально видимого сектора мы будем рисовать сетку, примитивы которой будут формировать ландшафт. Каждую из ее ячеек можно отобразить с помощью двух треугольников. Из-за того, что каждая ячейка имеет смежные грани, значения большинства вершин треугольников повторяются для двух или более ячеек. Чтобы не дублировать данные в буфере вершин, заполним буфер индексов. Если индексы используются, то с их помощью графический конвейер определяет, какой примитив в буфере вершин ему обрабатывать. (рис.5) Выбранная мной топология — triangle list (D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST)
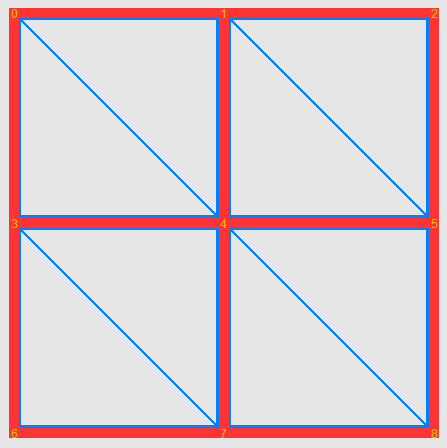
Рис.5 Визуальное отображение индексов и примитивов
Создавать для каждого сектора отдельный буфер вершин слишком накладно. Гораздо эффективнее использовать один буфер с координатами в пространстве сетки, то есть x — столбец, а у — строка. Но как из них получить точку на сфере? Сектор представляет из себя квадратную область с началом в некой точке S. Все секторы имеют одинаковую длину грани — назовем ее SLen. Сетка покрывает всю площадь сектора а также имеет одинаковое количество строк и столбцов, поэтому для нахождение длины грани ячейки мы можем построить следующее уравнение
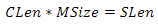
где СLen — длина грани ячейки, MSize — количество строк или столбцов сетки. Делим обе части на MSize и получаем CLen
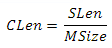
Идем далее. Пространство грани куба, которой принадлежит сектор, можно выразить как линейную комбинацию двух векторов единичной длины — назовем их V1 и V2. У нас выходит следующее уравнение(см. рис.6)
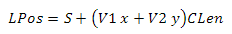
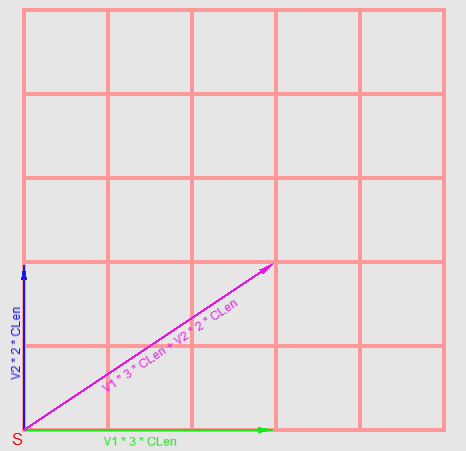
Рис.6 Наглядное отображение формирования точки на сетке
чтобы получить точку на сфере, воспользуемся уравнением, выведенным ранее
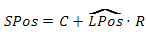
4. Высота
Все, чего мы добились к этому моменту, мало напоминает ландшафт. Пришло время добавить то, что сделает его таковым — разность высот. Давайте представим, что у нас есть сфера единичного радиуса с центром в начале координат, а также множество точек {P0, P1, P2… PN}, которые расположены на этой сфере. Каждую из этих точек можно представить как единичный вектор от начала координат. Теперь представьте, что у нас есть набор значений, каждое из которых является длиной конкретного вектора (рис.7).

Хранить эти значения я буду в двухмерной текстуре. Нам нужно найти связь между координатами пикселя текстуры и вектором-точкой на сфере. Приступим.
Помимо декартовой, точка на сфере также может быть описана с помощью сферической системы координат. В этом случае ее координаты будут состоять из трех элементов: азимутного угла, полярного угла и значения кратчайшего расстояния от начала координат до точки. Азимутный угол — это угол между осью X и проекцией луча от начала координат до точки на плоскость XZ. Он может принимать значения от нуля до 360 градусов. Полярный угол — угол между осью Y и лучом от начала координат до точки. Он также может называться зенитным или нормальным. Принимает значения от нуля до 180 градусов. (см. рис.8)
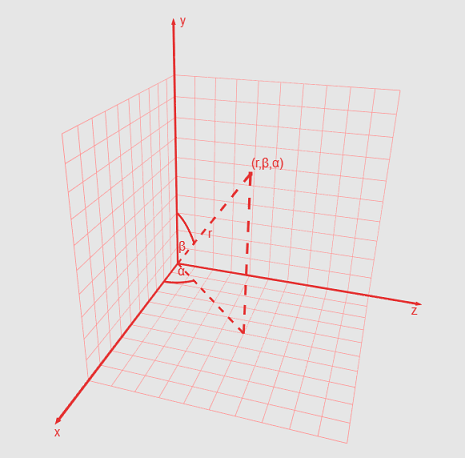
Рис.8 Сферические координаты
Для перехода из декартовой системы в сферическую я пользуюсь следующими уравнениями(я полагаю, что ось Y направлена вверх):
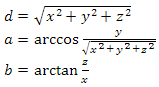
где d — расстояние до точки, a — полярный угол, b — азимутный угол. Параметр d также можно описать как «длина вектора от начала координат до точки»(что видно из уравнения). Если мы используем нормализованные координаты, то можем избежать деления при нахождении полярного угла. Собственно, зачем нам эти углы? Разделив каждый из них на его максимальный диапазон, мы получим коэффициенты от нуля до единицы и с их помощью произведем выборку из текстуры в шейдере. При получении коэффициента для полярного угла необходимо учитывать четверть, в которой расположен угол. «Но ведь значение выражения z / x не определено при x равном нулю» — скажете вы. Я более того скажу — при z равном нулю угол будет нулевым независимо от значения x. Давайте добавим несколько специальных случаев для этих значений. У нас есть нормализованные координаты(нормаль) — добавим несколько условий: если значение X нормали равно нулю и значение Z больше нуля — тогда коэффициент равен 0.25, если X нулевое и Z меньше нуля — то будет 0.75. Если же значение Z равно нулю и X меньше нуля, то в этом случае коэффициент будет равен 0.5. Все это легко проверить на окружности. Но как поступить, если Z нулевое и X больше нуля — ведь в таком случае будут корректными как 0 так и 1? Представим, что мы выбрали 1 — чтож, давайте возьмем сектор с минимальным азимутным углом 0 и максимальным — 90 градусов. Теперь рассмотрим первые три вершины в первой строке сетки, которая этот сектор отображает. Для первой вершины у нас выполнилось условие и мы установили для текстурной координаты X значение 1. Очевидно, что для последующих двух вершин это условие не выполнится — углы для них находятся в первой четверти и в результате мы получим примерно такой набор — (1.0, 0.05, 0.1). Но для сектора с углами от 270 до 360 для последних трех вершин в той же строке все будет корректно — сработает условие для последней вершины, и мы получим набор (0.9, 0.95, 1.0). Если же мы выберем в качестве результата ноль, то получим наборы (0.0, 0.05, 0.1) и (0.9, 0.95, 0.0) — в любом случае это приведет к довольно заметным искажениям поверхности. Поэтому давайте применим следующее. Возьмем центр сектора, затем нормализуем его центр, переместив тем самым на сферу. Теперь вычислим скалярное произведение нормализованного центра на вектор (0, 0, 1). Формально говоря этот вектор является нормалью к плоскости XY, и вычислив его скалярное произведение с нормализованным вектором центра сектора, мы сможем понять, с какой стороны от плоскости центр находится. Если оно меньше нуля, то сектор находится позади плоскости и нам нужно значение 1. Если скалярное произведение больше нуля, то сектор находится спереди от плоскости и поэтому граничным значением будет 0.(см. рис.9)

Рис.9 Проблема выбора между 0 и 1 для текстурных координат
Вот код получения текстурных координат из сферических. Обратите внимание — из-за погрешности в вычислениях мы не можем проверять значения нормали на равенство нулю, вместо этого мы должны сравнивать их абсолютные величины с неким пороговым значением (например 0.001)
//norm - нормализованные координаты точки, для которой мы получаем текстурные координаты
//offset - нормализованные координаты центра сектора, которому принадлежит norm
//zeroTreshold - пороговое значение (0.001)
float2 GetTexCoords(float3 norm, float3 offset)
{
float tX = 0.0f, tY = 0.0f;
bool normXIsZero = abs(norm.x) < zeroTreshold;
bool normZIsZero = abs(norm.z) < zeroTreshold;
if(normXIsZero || normZIsZero){
if(normXIsZero && norm.z > 0.0f)
tX = 0.25f;
else if(norm.x < 0.0f && normZIsZero)
tX = 0.5f;
else if(normXIsZero && norm.z < 0.0f)
tX = 0.75f;
else if(norm.x > 0.0f && normZIsZero){
if(dot(float3(0.0f, 0.0f, 1.0f), offset) < 0.0f)
tX = 1.0f;
else
tX = 0.0f;
}
}else{
tX = atan(norm.z / norm.x);
if(norm.x < 0.0f && norm.z > 0.0f)
tX += 3.141592;
else if(norm.x < 0.0f && norm.z < 0.0f)
tX += 3.141592;
else if(norm.x > 0.0f && norm.z < 0.0f)
tX = 3.141592 * 2.0f + tX;
tX = tX / (3.141592 * 2.0f);
}
tY = acos(norm.y) / 3.141592;
return float2(tX, tY);
}
приведу промежуточный вариант вершинного шейдера
//startPos - начало грани куба
//vec1, vec2 - векторы направления грани куба
//gridStep - размер ячейки
//sideSize - длина ребра сектора
//GetTexCoords() - преобразует сферические координаты в текстурные
VOut ProcessVertex(VIn input)
{
float3 planePos = startPos + vec1 * input.netPos.x * gridStep.x
+ vec2 * input.netPos.y * gridStep.y;
float3 sphPos = normalize(planePos);
float3 normOffset = normalize(startPos + (vec1 + vec2) * sideSize * 0.5f);
float2 tc = GetTexCoords(sphPos, normOffset);
float height = mainHeightTex.SampleLevel(mainHeightTexSampler, tc, 0).x;
posL = sphPos * (sphereRadius + height);
VOut output;
output.posH = mul(float4(posL, 1.0f), worldViewProj);
output.texCoords = tc;
return output;
}
5. Освещение
Чтобы реализовать зависимость цвета ландшафта от освещения, воспользуемся следующим уравнением:
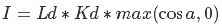
Где I — цвет точки, Ld — цвет источника света, Kd — цвет материала освещаемой поверхности, a — угол между вектором на источник и нормалью к освещаемой поверхности. Это частный случай закона косинусов Ламберта. Давайте разберемся, что здесь и почему. Под умножением Ld на Kd подразумевается покомпонентное умножение цветов, то есть (Ld.r * Kd.r, Ld.g * Kd.g, Ld.b * Kd.b). Возможно будет проще понять смысл, если представить следующую ситуацию: допустим, мы хотим осветить объект зеленым источником света, поэтому мы ожидаем, что цвет объекта будет в градациях зеленого. Результат (0 * Kd.r, 1 * Kd.g, 0 * Kd.b) дает (0, Kd.g, 0) — ровно то, что нам нужно. Идем далее. Как было озвучено ранее, косинусом угла между нормализованными векорами является их скалярное произведение. Давайте рассмотрим его максимальное и минимальное значение с нашей точки зрения. Если косинус угла между векторами равен 1, то этот угол равен 0 — следовательно, оба вектора коллинеарны (лежат на одной прямой). Тоже самое справедливо и для значения косинуса -1, только в этом случае векторы указывают в противоположных направлениях. Получается, чем ближе вектор нормали и вектор к источнику света к состоянию коллинеарности — тем выше коэффициент освещенности поверхности, которой принадлежит нормаль. Также предполагается, что поверхность не может быть освещена, если ее нормаль указывает в противоположную по отношению к направлению на источник сторону — именно поэтому я использую только положительные значения косинуса.Я использую параллельный источник, поэтому его позицией можно пренебречь. Единственное, что нужно учесть -то, что мы используем вектор на источник света. То есть, если направление лучей (1.0, -1.0, 0) — нам надо использовать вектор (-1.0, 1.0, 0). Единственное, что для нас представляет трудность — вектор нормали. Вычислить нормаль к плоскости просто — нам надо произвести векторное произведение двух векторов, которые ее описывают. Важно помнить что векторное произведение антикоммутативно — нужно учитывать порядок множителей. В нашем случае получить нормаль к треугольнику, зная координаты его вершин в пространстве сетки, можно следующим образом (Обратите внимание, что я не учитываю граничные случаи для p.x и p.y)
float3 p1 = GetPosOnSphere(p);
float3 p2 = GetPosOnSphere(float2(p.x + 1, p.y));
float3 p3 = GetPosOnSphere(float2(p.x, p.y + 1));
float3 v1 = p2 - p1;
float3 v2 = p3 - p1;
float3 n = normalzie(cross(v1, v2));
Но это еще не все. Большинство вершин сетки принадлежат сразу четырем плоскостям. Чтобы получить приемлемый результат, надо вычислить усредненную нормаль следующим образом:
Na = normalize(n0 + n1 + n2 + n3)
Реализовывать данный метод на GPU довольно затратно — нам потребуется два этапа на вычисление нормалей и их усреднение. К тому же эффективность оставляет желать лучшего. Исходя из этого я выбрал другой способ — использовать карту нормалей.(рис.10)

Рис.10 Карта нормалей
Принцип работы с ней такой же, как и с картой высот — преобразуем сферические координаты вершины сетки в текстурные и делаем выборку. Только вот напрямую эти данные мы использовать не сможем — ведь мы работаем со сферой, и у вершины есть своя нормаль, которую нужно учитывать. Поэтому данные карты нормалей мы будем использовать в качестве координат TBN базиса. Что такое базис? Вот вам такой пример. Представьте, что вы космонавт и сидите на маячке где-то в космосе. Вам из ЦУПа приходит сообщение: «Тебе нужно переместиться от маячка на 1 метр влево, на 2 метра вверх и на 3 метра вперед». Как это можно выразить математически? (1, 0, 0) * 1 + (0, 1, 0) * 2 + (0, 0, 1) * 3 = (1,2,3). В матричной форме данное уравнение можно выразить так:
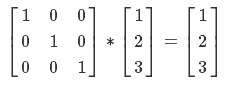
Теперь представьте, что вы также сидите на маячке, только теперь вам из ЦУПа пишут: «мы там тебе векторы направлений прислали — ты должен продвинуться 1 метра по первому вектору, 2 метра по второму и 3 — по третьему». Уравнение для новых координат будет таким:
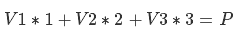
покомпонентная запись выглядит так:
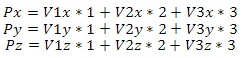
Или в матричной форме:
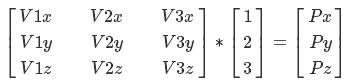
так вот, матрица с векторами V1, V2 и V3 — это базис, а вектор (1,2,3) — координаты в пространстве этого базиса.
Представим теперь, что у вас есть набор векторов (базис M) и вы знаете, где вы находитесь относительно маячка (точка P). Вам нужно узнать ваши координаты в пространстве этого базиса — на сколько вам нужно продвинуться по этим векторам, чтобы оказаться в том же месте. Представим искомые координаты (X)
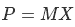
Будь P, M и X числами, мы бы просто разделили обе части уравнения на M, но увы… Пойдем другим путем — согласно свойству обратной матрицы
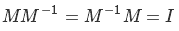
где I это единичная матрица. В нашем случае она выглядит так
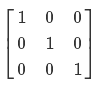
Что это нам дает? Попробуйте умножить это матрицу на X и вы получите
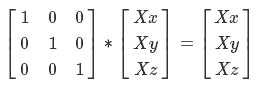
Также надо уточнить, что умножение матриц обладает свойством ассоциативности
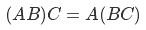
Вектор мы вполне законно можем рассматривать как матрицу 3 на 1
Учитывая все вышесказанное, можно слелать вывод, что чтобы получить Х в правой части уравнения, нам нужно в правильном порядке умножить обе части на обратную M матрицу
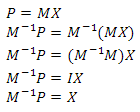
Этот результат понадобится нам в дальнейшем
Теперь вернемся к нашей проблеме. Я буду использовать ортонормированный базис — это значит, что V1, V2 и V3 ортогональны по отношению друг к другу(образуют угол 90 градусов) и имеют единичную длину. В качестве V1 будет выступать tangent вектор, V2 — bitangent вектор, V3 — нормаль. В традиционном для DirectX транспонированном виде матрица выглядит так:
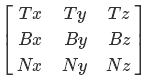
где T — tangent вектор, B — bitangent вектор и N — нормаль. Давайте найдем их. С нормалью проще всего-по сути это нормализованные координаты точки. Bitangent вектор равен векторному произведению нормали и tangent вектора. Сложнее всего придется с tangent вектором. Он равен направлению касательной к окружности в точке. Давайте разберем этот момент. Сперва найдем координаты точки на единичной окружности в плоскости XZ для некоторого угла a
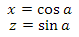
Направление касательной к окружности в этой точке можно найти двумя способами. Вектор до точки на окружности и вектор касательной ортогональны — поэтому, так как функции sin и cos периодические — мы можем просто прибавить pi/2 к углу a и получим искомое направление. Согласно свойству смещения на pi/2:
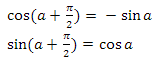
у нас получился следующий вектор:
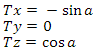
Мы также можем воспользоваться дифференцированием — подробнее см. в Приложении 3. Итак, на рисунке 11 вы можете видеть сферу, для каждой вершины которой построен базис. Синими векторами обозначены нормали, красными — tangent векторы, зелеными — bitangent векторы.
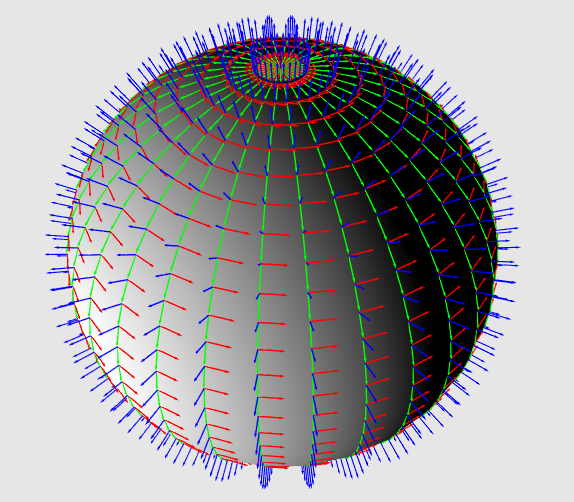
Рис.11 Сфера с TBN базисами в каждой вершине. Красные — tangent векторы, зеленые — bitangent векторы, синие векторы — нормали
С базисом разобрались — теперь давайте получим карту нормалей. Для этого воспользуемся фильтром Собеля. Фильтр Собеля вычисляет градиент яркости изображения в каждой точке(грубо говоря, вектор изменения яркости). Принцип действия фильтра заключается в том, что нужно применить некую матрицу значений, которая назвается «Ядром», к каждому пикселю и его соседям в пределах размерности этой матрицы. Предположим, что мы обрабатываем пиксель P ядром K. Если он не находится на границе изображения, то у него есть восемь соседей — левый верхний, верхний, правый верхний и так далее. Назовем их tl, t, tb, l, r, bl, b, br. Так вот, применение ядра K к этому пикселю заключается в следующем:
Pn = tl * K(0, 0) + t * K(0,1) + tb * K(0,2) +
          l * K(1, 0) + P * K(1,1) + r * K(1,2) +
          bl * K(2, 0) + b * K(2,1) + br * K(2,2)
Этот процесс называется «Свертка». Фильтр Собеля использует два ядра для вычисления градиента по вертикали и горизонтали. Обозначим их как Kx и Kу:
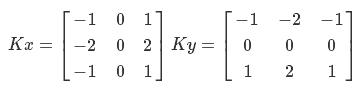
Основа есть — можно приступать к реализации. Сперва нам надо вычислить яркость пикселя. Я пользуюсь преобразованием из цветовой модели RGB в модель YUV для системы PAL:
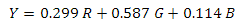
Но так как наше изображение изначально в градациях серого, то этот этап можно пропустить. Теперь нам нужно «свернуть» исходное изображение с ядрами Kx и Ky. Так мы получим компоненты X и Y градиента. Также очень полезным может оказаться значение нормали этого вектора — его мы использовать не будем, но у избражений, содержащих нормализованные значения нормали градиента, есть несколько полезных применений. Под нормализацией я имею ввиду следующее уравнение
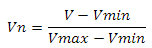
где V — значение, которое нормализуем, Vmin и Vmax — область этих значений. В нашем случае минимальное и максимальное значения отслеживаются в процессе генерации. Вот пример реализации фильтра Собеля:
float SobelFilter::GetGrayscaleData(const Point2 &Coords)
{
Point2 coords;
coords.x = Math::Saturate(Coords.x, RangeI(0, image.size.width - 1));
coords.y = Math::Saturate(Coords.y, RangeI(0, image.size.height - 1));
int32_t offset = (coords.y * image.size.width + coords.x) * image.pixelSize;
const uint8_t *pixel = &image.pixels[offset];
return (image.pixelFormat == PXL_FMT_R8) ? pixel[0] : (0.30f * pixel[0] + //R
0.59f * pixel[1] + //G
0.11f * pixel[2]); //B
}
void SobelFilter::Process()
{
RangeF dirXVr, dirYVr, magNormVr;
for(int32_t y = 0; y < image.size.height; y++)
for(int32_t x = 0; x < image.size.width; x++){
float tl = GetGrayscaleData({x - 1, y - 1});
float t = GetGrayscaleData({x , y - 1});
float tr = GetGrayscaleData({x + 1, y - 1});
float l = GetGrayscaleData({x - 1, y });
float r = GetGrayscaleData({x + 1, y });
float bl = GetGrayscaleData({x - 1, y + 1});
float b = GetGrayscaleData({x , y + 1});
float br = GetGrayscaleData({x + 1, y + 1});
float dirX = -1.0f * tl + 0.0f + 1.0f * tr +
-2.0f * l + 0.0f + 2.0f * r +
-1.0f * bl + 0.0f + 1.0f * br;
float dirY = -1.0f * tl + -2.0f * t + -1.0f * tr +
0.0f + 0.0f + 0.0f +
1.0f * bl + 2.0f * b + 1.0f * br;
float magNorm = sqrtf(dirX * dirX + dirY * dirY);
int32_t ind = y * image.size.width + x;
dirXData[ind] = dirX;
dirYData[ind] = dirY;
magNData[ind] = magNorm;
dirXVr.Update(dirX);
dirYVr.Update(dirY);
magNormVr.Update(magNorm);
}
if(normaliseDirections){
for(float &dirX : dirXData)
dirX = (dirX - dirXVr.minVal) / (dirXVr.maxVal - dirXVr.minVal);
for(float &dirY : dirYData)
dirY = (dirY - dirYVr.minVal) / (dirYVr.maxVal - dirYVr.minVal);
}
for(float &magNorm : magNData)
magNorm = (magNorm - magNormVr.minVal) / (magNormVr.maxVal - magNormVr.minVal);
}
Надо сказать, что фильтр Собеля обладает свойством линейной сепарабельности, поэтому данный метод может быть оптимизирован.
Сложная часть закончилась — осталось записать X и Y координаты направления градиента в R и G каналы пикселей карты нормалей.Для координаты Z я использую еденицу. Также я использую трехмерный вектор коэффициентов для настройки этих значений. Далее приведен пример генерации карты нормалей с комментариями:
//ImageProcessing::ImageData Image - оригинальное изображение. Структора содержит формат пикселя и данные изображения
ImageProcessing::SobelFilter sobelFilter;
sobelFilter.Init(Image);
sobelFilter.NormaliseDirections() = false;
sobelFilter.Process();
const auto &resX =sobelFilter.GetFilteredData(ImageProcessing::SobelFilter::SOBEL_DIR_X);
const auto &resY =sobelFilter.GetFilteredData(ImageProcessing::SobelFilter::SOBEL_DIR_Y);
ImageProcessing::ImageData destImage = {DXGI_FORMAT_R8G8B8A8_UNORM, Image.size};
size_t dstImageSize = Image.size.width * Image.size.height * destImage.pixelSize;
std::vector<uint8_t> dstImgPixels(dstImageSize);
for(int32_t d = 0 ; d < resX.size(); d++){
//используем вектор настроечных коэффициентов. У меня он равен (0.03, 0.03, 1.0)
Vector3 norm = Vector3::Normalize({resX[d] * NormalScalling.x,
resY[d] * NormalScalling.y,
1.0f * NormalScalling.z});
Point2 coords(d % Image.size.width, d / Image.size.width);
int32_t offset = (coords.y * Image.size.width + coords.x) * destImage.pixelSize;
uint8_t *pixel = &dstImgPixels[offset];
//переводим значения из области [-1.0, 1.0] в [0.0, 1.0] а затем в область [0, 256]
pixel[0] = (0.5f + norm.x * 0.5f) * 255.999f;
pixel[1] = (0.5f + norm.y * 0.5f) * 255.999f;
pixel[2] = (0.5f + norm.z * 0.5f) * 255.999f;
}
destImage.pixels = &dstImgPixels[0];
SaveImage(destImage, OutFilePath);
Теперь приведу пример использования карты нормалей в шейдере:
//texCoords - текстурные коорлинаты которые мы получили способом, описанным в п.4
//normalL - нормаль вершины
//lightDir - вектор на источник света
//Ld - цвет источника света
//Kd - цвет материала освещаемой поверхности
float4 normColor = mainNormalTex.SampleLevel(mainNormalTexSampler, texCoords, 0);
//переводим значение из области [0.0, 1.0] в [-1.0, 1.0] и нормализуем результат
float3 normalT = normalize(2.0f * mainNormColor.rgb - 1.0f);
//переводим текстурную координату Х из области [0.0, 1.0] в [0.0, Pi*2.0]
float ang = texCoords.x * 3.141592f * 2.0f;
float3 tangent;
tangent.x = -sin(ang);
tangent.y = 0.0f;
tangent.z = cos(ang);
float3 bitangent = normalize(cross(normalL, tangent));
float3x3 tbn = float3x3(tangent, bitangent, normalL);
float3 resNormal = mul(normalT, tbn);
float diff = saturate(dot(resNormal, lightDir.xyz));
float4 resColor = Ld * Kd * diff;
6. Level Of Detail
Ну вот, теперь наш ландшафт освещен! Можно лететь на Луну — загураем карту высот, ставим цвет материала, загружаем секторы, устанавливаем размер сетки равным {16, 16} и… Да, что-то маловато — поставлю ка я {256, 256} — ой, что-то все тормозит, да и зачем высокая детализация на дальних секторах? К томуже, чем ближе наблюдатель к планете, тем меньше секторов он может увидеть. Да… походу у нас еще много работы! Давайте сперва разберемся, как отсечь лишние секторы. Определяющей величиной здесь будет высота наблюдателя от поверхности планеты — чем она выше, тем больше секторов он может увидеть (рис.12)
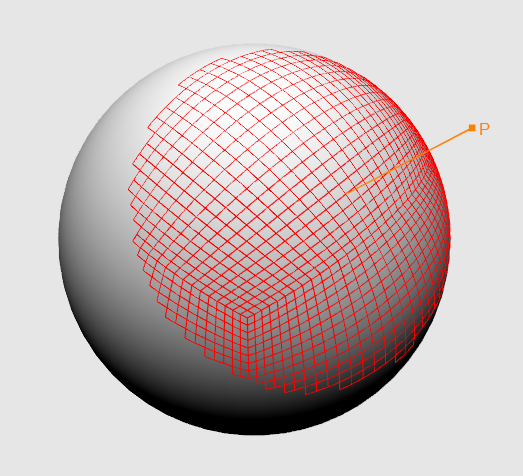
Рис.12 Зависимость высоты наблюдателя от кол-ва обрабатываемых секторов
Высоту находим следующим образом — строим вектор от позиции наблюдателя на центр сферы, вычисляем его длину и отнимаем от нее значение радиуса сферы. Ранее я говорил, что если скаларное произведение вектора на наблюдателя и вектора на центр сектора меньше нуля, то этот сектор нас не интересует — теперь вместо нуля мы мы будем использовать значение, линейно зависимое от высоты. Сперва давайте определимся с переменными — итак, у нас будут минимальное и максимальное значения скалярного произведения и минимальное и максимальное значение высоты. Построим следующую систему уравнений
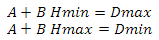
Теперь выразим А во втором уравнении
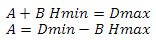
подставим А из второго уравнения в первое
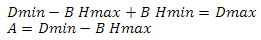
выразим B из первого уравнения
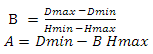
подставим B из первого уравнения во второе
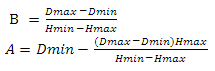
Теперь подставим переменные в функцию
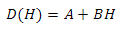
и получим
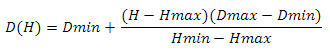
Где Hmin и Hmax-минимальное и максимальное значение высоты, Dmin и Dmax — минимальное и максимальное значения скалярного произведения. Эту задачу можно решить иначе — см. приложение 4.
Теперь нужно разобраться с уровнями детализации. Каждый из них будет определять область значения скалярного произведения. В псевдокоде процесс определения принадлежности сектора определенному уровню выглядит так:
цикл по всем секторам
вычисляем скалярное произведение вектора на наблюдателя и вектора на центр сектора
если скалярное произведение меньше минимального порога, вычисленного ранее
переходим к следующему сектору
цикл по уровням детализации
если скалярное произведение находится в рамках определенных для этого уровня
добавляем сектор к этому уровню
конец цикла по уровням детализации
конец цикла по всем секторам
Нам надо вычислить область значения для каждого уровня. Сначала построим систему из двух уравнений
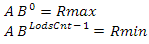
решив ее, получим
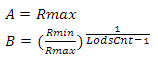
Используя эти коэффициенты, определим функцию
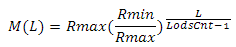
где Rmax это область значения скалярного произведения (D(H) — Dmin), Rmin — минимальная область, определяемая уровнем. Я использую значение 0.01. Теперь нам нужно отнять результат от Dmax
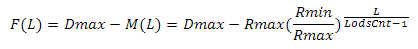
C помощью этой функции мы получим области для всех уровней. Вот пример:
const float dotArea = dotRange.maxVal - dotRange.minVal;
const float Rmax = dotArea, Rmin = 0.01f;
float lodsCnt = lods.size();
float A = Rmax;
float B = powf(Rmin / Rmax, 1.0f / (lodsCnt - 1.0f));
for(size_t g = 0; g < lods.size(); g++){
lods[g].dotRange.minVal = dotRange.maxVal - A * powf(B, g);
lods[g].dotRange.maxVal = dotRange.maxVal - A * powf(B, g + 1);
}
lods[lods.size() - 1].dotRange.maxVal = 1.0f;
Теперь мы можем определить, к какому уровню детализации принадлежит сектор (рис.13).

Рис.13 Цветовая дифференциация секторов согласно уровням детализации
Далее надо разобраться с размерами сеток. Хранить для каждого уровня свою сетку будет очень накладно — гораздо эффективнее менять детализацию одной сетки на лету с помощью тесселяции. Для этого нам надо помимо превычных вершинного и пиксельного, также реализовать hull и domain шейдеры. В Hull шейдере основная задача — подготовить контрольные точки. Он состоит из двух частей — основной функции и функции, вычисляющей параметры контрольной точки. Обязательно нужно указать значения для следующих атрибутов:
domain
partitioning
outputtopology
outputcontrolpoints
patchconstantfunc
Вот пример Hull шейдера для разбиения треугольниками:
struct PatchData
{
float edges[3] : SV_TessFactor;
float inside : SV_InsideTessFactor;
};
PatchData GetPatchData(InputPatch<VIn, 3> Patch, uint PatchId : SV_PrimitiveID)
{
PatchData output;
flloat tessFactor = 2.0f;
output.edges[0] = tessFactor;
output.edges[1] = tessFactor;
output.edges[2] = tessFactor;
output.inside = tessFactor;
return output;
}
[domain("tri")]
[partitioning("integer")]
[outputtopology("triangle_cw")]
[outputcontrolpoints(3)]
[patchconstantfunc("GetPatchData")]
VIn ProcessHull(InputPatch<VIn, 3> Patch,
uint PointId : SV_OutputControlPointID,
uint PatchId : SV_PrimitiveID)
{
return Patch[PointId];
}
Видите, основная работа выполняется в GetPatchData(). Ее задача — установить фактор тесселяции. О нем мы поговорим позднее-сейчас перейдем к Domain шейдеру. Он получает контрольные точки от Hull шейдера и координаты от тесселятора. Новое значение позиции или текстурных координат в случае разбиения треугольниками нужно вычислять по следующей формуле
N = C1 * F.x + C2 * F.y + C3 * F.z
где C1, C2 и C3 — значения контрольных точек, F — координаты тесселятора. Также в Domain шейдере нужно установить атрибут domain, значение которого соответствует тому, которое было указано в Hull шейдере. Вот пример Domain шейдера:
cbuffer buff0 : register(b0)
{
matrix worldViewProj;
}
struct PatchData
{
float edges[3] : SV_TessFactor;
float inside : SV_InsideTessFactor;
};
[domain("quad")]
PIn ProcessDomain(PatchData Patch,
float3 Coord : SV_DomainLocation,
const OutputPatch<VIn, 3> Tri)
{
float3 posL = Tri[0].posL * Coord.x +
Tri[1].posL * Coord.y +
Tri[2].posL * Coord.z;
float2 texCoords = Tri[0].texCoords * Coord.x +
Tri[1].texCoords * Coord.y +
Tri[2].texCoords * Coord.z;
PIn output;
output.posH = mul(float4(posL, 1.0f), worldViewProj);
output.normalW = Tri[0].normalW;
output.texCoords = texCoords;
return output;
}
Роль вершинного шейдера в этом случае сведена к минимуму — у меня он просто «прокидывает» данные на следующий этап.
Теперь нужно реализовать нечто подобное. Наша первостепенная задача — вычислить фактор тесселяции, а если точнее, то построить его зависимость от высоты наблюдателя. Снова построим систему уравнений
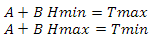
решив ее таким же способом, как и ранее, получим
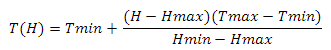
где Tmin и Tmax — минимальный и максимальный коэффициенты тесселяции, Hmin и Hmax — минимальное и максимальное значения высоты наблюдателя. Минимальный коэффициент тесселяции у меня равен единице. максимальный устанавливается отдельно для каждого уровня
(например 1, 2, 4, 16).
В дальнейшем нам будет необходимо, чтобы рост фактора был ограничен ближайшей степенью двойки. то есть для значений от двух до трех мы устанавливаем значение два, для значений от 4 до 7 установим 4, при значениях от 8 до 15 фактор будет равен 8 и т.д. Давайте решим эту задачу для фактора 6. Сперва решим следующее уравнение
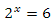
давайте возьмем десятичный логарифм от двух частей уравнения
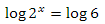
согласно свойству логарифмов, мы можем переписать уравнение следующим образом
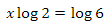
теперь нам остается разделить обе части на log(2)
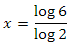
Но это еще не все. Х равен приблизительно 2.58. Далее нужно сбросить дробную часть и возвести двойку в степень получившегося числа. Вот код вычисления факторов тесселяции для уровней детализации
float h = camera->GetHeight();
const RangeF &hR = heightRange;
for(LodsStorage::Lod &lod : lods){
//derived from system
//A + B * Hmax = Lmin
//A + B * Hmin = Lmax
//and getting A then substitution B in second equality
float mTf = (float)lod.GetMaxTessFactor();
float tessFactor = 1.0f + (mTf - 1.0f) * ((h - hR.maxVal) / (hR.minVal - hR.maxVal));
tessFactor = Math::Saturate(tessFactor, RangeF(1.0f, mTf));
float nearPowOfTwo = pow(2.0f, floor(log(tessFactor) / log(2)));
lod.SetTessFactor(nearPowOfTwo);
}
7. Шум
Давайте посмотрим, как можно увеличить детализацию ландшафта, не изменяя при этом размер карты высот. Мне на ум приходит следующее — изменять значение высоты на значение, полученное из текстуры градиентного шума. Координаты, по которым мы будем осуществлять выборку, будут в N раз больше основных. При выборке будет задействован зеркальный тип адресации (D3D11_TEXTURE_ADDRESS_MIRROR) (см. рис.14).

Рис.14 Сфера с картой высот + сфера с шумовой картой = сфера с итоговой высотой
В этом случае высота будет вычисляться следующим образом:
//float2 tc1 - текстурные координаты, полученные из нормализованной точки, как было
//рассказано ранее
//texCoordsScale - множитель текстурных координат. В моем случае равен значению 300
//mainHeightTex, mainHeightTexSampler - текстура карты высот
//distHeightTex, distHeightTexSampler - текстура градиентного шума
//maxTerrainHeight - максимальная высота ландшафта. В моем случае 0.03
float2 tc2 = tc1 * texCoordsScale;
float4 mainHeighTexColor = mainHeightTex.SampleLevel(mainHeightTexSampler, tc1, 0);
float4 distHeighTexColor = distHeightTex.SampleLevel(distHeightTexSampler, tc2, 0);
float height = (mainHeighTexColor.x + distHeighTexColor.x) * maxTerrainHeight;
Пока что периодический характер выражается значительно, но с добавлением освещения и текстурирования ситуация изменится в лучшую сторону. А что такое из себя представляет текстура градиентного шума? Грубо говоря это решётка из случайных значений. Давайте разберемся, как сопоставить размеры решетки размеру текстуры. Предположим мы хотим создать шумовую текстуру размера 256 на 256 пикселей. Все просто, если размеры решетки совпадают с размерами текстуры — у нас получится что-то подобное белому шуму в телевизоре. А как быть, если наша решетка имеет размеры, скажем, 2 на 2? Ответ прост — использовать интерполяцию. Одна из формулировок линейной интерполяции выглядит так:
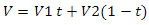
Это самый быстрый, но в тоже время наименее подходящий нам вариант. Лучше использовать интерполяцию на основе косинуса:
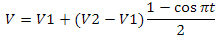
Но мы не можем просто интерполировать между значениями по краям диагонали (левым нижним и правым верхним углом ячейки). В нашем случае интерполяцию нужно будет применять дважды. Давайте предствим одну из ячеек решетки. У нее есть четыре угла — назовем их V1, V2, V3, V4. Также внутри этой ячейки будет своя двухмерная система координат, где точка (0, 0) соответствует V1 и точка (1, 1) — V3 (см. рис.15a). Для того, чтобы получить значение с координатами (0.5, 0.5), нам сперва нужно получить два интерполированных по Х значения — между V1 и V4 и между V2 и V3, и наконец интерполировать по Y между этими значениями(рис.15b).
Вот пример:
float2 coords(0.5f, 0.5f)
float4 P1 = lerp(V1, V4, coords.x);
float4 P2 = lerp(V2, V3, coords.x);
float4 P = lerp(P1, P2, coords.y)
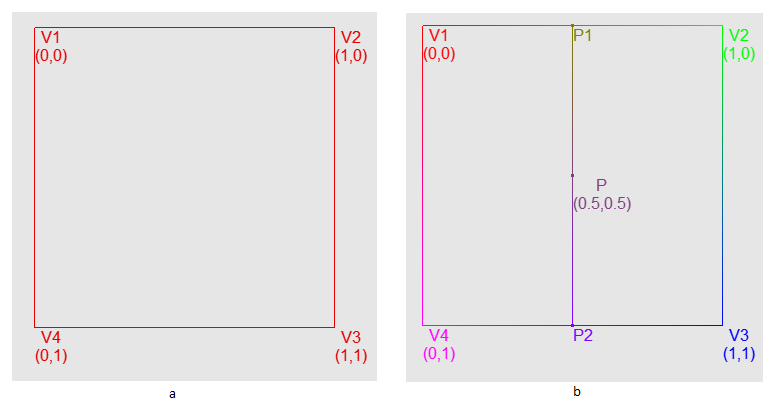
Рис.15 a — Изображение ячейки решетки с координатами V1, V2, V3 и V4. b — Последовательность двух интерполяций на примере ячейки
теперь давайте сделаем следующее — для каждого пикселя шумовой текстуры возьмем интерполированное значение для сетки 2х2, затем прибавим к нему интерполированное значение для сетки 4х4, умноженное на 0.5, затем для сетки 8х8, умноженное на 0.25 и т.д до определенного предела — это назвается сложение октав (рис.16). Формула выглядит так:
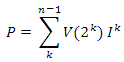

Рис.16 Пример сложения октав
Вот пример реализации:
for(int32_t x = 0; x < size.width; x++)
for(int32_t y = 0; y < size.height; y++){
float val = 0.0f;
Vector2 normPos = {(float)x / (float)(sideSize - 1),
(float)y / (float)(sideSize - 1)};
for(int32_t o = 0; o < octavesCnt; o++){
float frequency = powf(2.0f, (float)(startFrequency + o));
float intencity = powf(intencityFactor, (float)o);
Vector2 freqPos = normPos * frequency;
Point2 topLeftFreqPos = Cast<Point2>(freqPos);
Point2 btmRightFreqPos = topLeftFreqPos + Point2(1, 1);
float xFrac = freqPos.x - (float)topLeftFreqPos.x;
float yFrac = freqPos.y - (float)topLeftFreqPos.y;
float iVal = GetInterpolatedValue(topLeftFreqPos,
btmRightFreqPos,
xFrac,
yFrac);
val += iVal * intencity;
}
noiseValues[y * size.width + x] = val;
}
Также для V1, V2, V3 и V4 вы можете получить сумму от самого значения и его соседей следующим образом:
float GetSmoothValue(const Point2 &Coords)
{
float corners = (GetValue({Coords.x - 1, Coords.y - 1}) +
GetValue({Coords.x + 1, Coords.y - 1}) +
GetValue({Coords.x - 1, Coords.y + 1}) +
GetValue({Coords.x + 1, Coords.y + 1})) / 16.0f;
float sides = (GetValue({Coords.x - 1, Coords.y}) +
GetValue({Coords.x + 1, Coords.y}) +
GetValue({Coords.x, Coords.y - 1}) +
GetValue({Coords.x, Coords.y + 1})) / 8.0f;
float center = GetValue(Coords) / 4.0f;
return center + sides + corners;
}
и использовать эти значения при интерполяции. Вот остальной код:
float GetInterpolatedValue(const Point2 &TopLeftCoord,
const Point2 &BottomRightCoord,
float XFactor,
float YFactor)
{
Point2 tlCoords(TopLeftCoord.x, TopLeftCoord.y);
Point2 trCoords(BottomRightCoord.x, TopLeftCoord.y);
Point2 brCoords(BottomRightCoord.x, BottomRightCoord.y);
Point2 blCoords(TopLeftCoord.x, BottomRightCoord.y);
float tl = (useSmoothValues) ? GetSmoothValue(tlCoords) : GetValue(tlCoords);
float tr = (useSmoothValues) ? GetSmoothValue(trCoords) : GetValue(trCoords);
float br = (useSmoothValues) ? GetSmoothValue(brCoords) : GetValue(brCoords);
float bl = (useSmoothValues) ? GetSmoothValue(blCoords) : GetValue(blCoords);
float bottomVal = Math::CosInterpolation(bl, br, XFactor);
float topVal = Math::CosInterpolation(tl, tr, XFactor);
return Math::CosInterpolation(topVal, bottomVal, YFactor);
}
В заключении подраздела хочу сказать, что все описанное мной до этого момента — несколько отличающаяся от канонической реализация шума Перлина.
С высотой разобрались — теперь давайте посмотрим, как быть с нормалями. Как и в случае с основной карты высот, из текстры шума нам надо сгенерировать карту нормалей. Затем в шейдере мы просто складываем нормаль из основной карты с нормалью из шумовой текстуры. Надо сказать, что это не совсем корректно, но дает приемлимый результат. Вот пример:
//float2 texCoords1 - текстурные координаты, полученные из нормализованной точки, как было рассказано ранее
//mainNormalTex, mainNormalTexSampler - основная карта нормалей
//distNormalTex, distNormalTexSampler - карта нормалей градиентного шума
float2 texCoords2 = texCoords1 * texCoordsScale;
float4 mainNormColor = mainNormalTex.SampleLevel(mainNormalTexSampler, TexCoords1, 0);
float4 distNormColor = distNormalTex.SampleLevel(distNormalTexSampler, TexCoords2, 0);
float3 mainNormal = 2.0f * mainNormColor.rgb - 1.0f;
float3 distNormal = 2.0f * distNormColor.rgb - 1.0f;
float3 normal = normalize(mainNormal + distNormal);
8. Hardware Instancing
Займемся оптимизацией. Сейчас цикл отрисовки секторов в псевдокоде выглядит так
цикл по всем секторам
вычисляем скаларное произведение вектора на точку и вектора на центр сектора
если оно больше нуля
устанавливаем значение S в данных шейдера
устанавливаем значение V1 в данных шейдера
устанавливаем значение V2 в данных шейдера
отрисовываем сетку
конец условия
конец цикла по всем секторам
производительность даного подхода чрезвычайно мала. Вариантов оптимизации несколько — можно построить квадродерево для каждой плоскости куба, чтобы не вычислять скалярное произведение для каждого сектора. Также можно обновлять значения V1 и V2 не для каждого сектора, а для шести плоскостей куба, кторым они принадлежат. Я выбрал третий вариант — Instancing. Вкратце о том, что это такое. Допустим, вы хотите нарисовать лес. У вас есть модель дерева, также имеется набор матриц преобразований — позиции деревьев, возможное масштабирование или поворот. Вы можете создать один буфер, в котором будут содержаться преобразованные в мировое пространство вершины всех деревьев — вариант неплохой, лес по карте не бегает. А что если вам надо реализовывать преобразования — скажем, покачивания деревьев на ветру. Можно сделать так — копируем данные вершин модели N раз в один буфер, добавляя к данным вершины индекс дерева (от 0 до N). Далее обновляем массив матриц преобразований и передаем его как переменную в шейдер. В шейдере мы выбираем нужную матрицу по индексу дерева. Как можно избежать дублирования данных? Для начала хочу обратить ваше внимание, что данные вершины можно собрать из нескольких буферов. Для при описании вершины нужно указать индекс источника в поле InputSlot структуры D3D11_INPUT_ELEMENT_DESC. Это можно использовать при реализации морфирующей лицевой анимации — скажем у вас есть два буфера вершин, содержаших два состояния лица, и вы хотите линейно интерполировать эти значения. Вот как нужно описать вершину:
D3D11_INPUT_ELEMENT_DESC desc[] = {
/*part1*/
{"POSITION", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 0, D3D11_INPUT_PER_VERTEX_DATA, 0},
{"NORMAL", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 12, D3D11_INPUT_PER_VERTEX_DATA, 0},
{"TEXCOORD", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 24, D3D11_INPUT_PER_VERTEX_DATA, 0},
/*part2*/
{"POSITION", 1, DXGI_FORMAT_R32G32B32_FLOAT, 1, 0, D3D11_INPUT_PER_VERTEX_DATA, 0},
{"NORMAL", 1, DXGI_FORMAT_R32G32B32_FLOAT, 1, 12, D3D11_INPUT_PER_VERTEX_DATA, 0},
{"TEXCOORD", 1, DXGI_FORMAT_R32G32B32_FLOAT, 1, 24, D3D11_INPUT_PER_VERTEX_DATA, 0}
}
в шейдере вершину нужно описать так:
struct VIn
{
float3 position1 : POSITION0;
float3 normal1 : NORMAL0;
float2 tex1 : TEXCOORD0;
float3 position2 : POSITION1;
float3 normal2 : NORMAL1;
float2 tex2 : TEXCOORD1;
}
далее вы просто интерполируете значения
float3 res = lerp(input.position1, input.position2, factor);
К чему я это? Вернемся к примеру с деревьями. Вершину будем собирать из двух источников — первый будет содержать позицию в локальном пространстве, текстурные координаты и нормаль, второй — матрицу преобразования в виде четырех четырехмерных векторов. Описание вершины выглядит так:
D3D11_INPUT_ELEMENT_DESC desc[] = {
/*part1*/
{"POSITION", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 0, D3D11_INPUT_PER_VERTEX_DATA, 0},
{"NORMAL", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 12, D3D11_INPUT_PER_VERTEX_DATA, 0},
{"TEXCOORD", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 24, D3D11_INPUT_PER_VERTEX_DATA, 0},
/*part2*/
{"WORLD", 0, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 0, D3D11_INPUT_PER_INSTANCE_DATA, 1},
{"WORLD", 1, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 16, D3D11_INPUT_PER_INSTANCE_DATA, 1},
{"WORLD", 2, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 32, D3D11_INPUT_PER_INSTANCE_DATA, 1},
{"WORLD", 3, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 48, D3D11_INPUT_PER_INSTANCE_DATA, 1},
}
Обратите внимание, что во второй части поле InputSlotClass равно D3D11_INPUT_PER_INSTANCE_DATA и поле InstanceDataStepRate равно единице (Краткое описание поля InstanceDataStepRate см. в приложении 1). В этом случае сборщик будет использовать данные всего буфера из источника с типом D3D11_INPUT_PER_VERTEX_DATA для каждого элемента из источника с типом D3D11_INPUT_PER_INSTANCE_DATA. При этом в шейдере данные вершины можно описать следующим образом:
struct VIn
{
float3 posL : POSITION;
float3 normalL : NORMAL;
float2 tex : TEXCOORD;
row_major float4x4 world : WORLD;
};
Создав второй буфер с атрибутами D3D11_USAGE_DYNAMIC и D3D11_CPU_ACCESS_WRITE, мы сможем обновлять его со стороны CPU. Отрисовывать такого рода геометрию нужно с помощью вызовов DrawInstanced() или DrawIndexedInstanced(). Есть еще вызовы DrawInstancedIndirect() и DrawIndexedInstancedIndirect() — про них см. в приложении 2.
Приведу пример установки буферов и использования функции DrawIndexedInstanced():
//vb - вершинный буфер
//tb - "истансный" буфер
//ib - индексный буфер
//vertexSize - размер элемента в вершинном буфере
//instanceSize - размер элемента в "инстансном" буфере
//indicesCnt - количество индексов
//instancesCnt - количество "инстансев"
std::vector<ID3D11Buffer*> buffers = {vb, tb};
std::vector<UINT> strides = {vertexSize, instanceSize};
std::vector<UINT> offsets = {0, 0};
deviceContext->IASetVertexBuffers(0,buffers.size(),&buffers[0],&strides[0],&offsets[0]);
deviceContext->IASetIndexBuffer(ib, DXGI_FORMAT_R32_UINT, 0);
deviceContext->IASetPrimitiveTopology(D3D11_PRIMITIVE_TOPOLOGY_TRIANGLELIST);
deviceContext->DrawIndexedInstanced(indicesCnt, instancesCnt, 0, 0, 0);
Теперь давайте наконец вернемся к нашей теме. Сектор мужно описать точкой на плоскости, которой он принадлежит и двумя векторами, которые эту плоскость описывают. Следовательно вершина будет состоять из двух источников. Первый — координаты в пространстве сетки, второй — данные сектора. Описание вершины выглядит так:
std::vector<D3D11_INPUT_ELEMENT_DESC> meta = {
//координаты в пространстве сетки
{"POSITION", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 0, D3D11_INPUT_PER_VERTEX_DATA, 0}
//первый вектор грани
{"TEXCOORD", 0, DXGI_FORMAT_R32G32B32_FLOAT, 1, 0, D3D11_INPUT_PER_INSTANCE_DATA, 1},
//второй вектор грани
{"TEXCOORD", 1, DXGI_FORMAT_R32G32B32_FLOAT, 1, 12, D3D11_INPUT_PER_INSTANCE_DATA, 1},
//начало грани
{"TEXCOORD", 2, DXGI_FORMAT_R32G32B32_FLOAT, 1, 24, D3D11_INPUT_PER_INSTANCE_DATA, 1}
}
Обратите внимание, что для хранения координат в пространстве сетки я использую трехмерный вектор (координата z не используется)
9. Frustum culling
Еще один важный компонент оптимизации — отсечение по пирамиде видимости (Frustum culling). Пирамида видимости — это та область сцены, которую «видит» камера. Как ее построить? Сперва вспомним, что точка может быть в четырех системах координат — локальной, мировой, видовой и системе координат проекции. Переход между ними осуществляется посредством матриц — мировой, видовой и матрицы проекции, причем преобразования должны проходить последовательно — от локального в мировое, из мирового в видовое и наконец из видового в пространство проекции. Все эти преобразования можно объединить в одно посредством умножения этих матриц.
     Мы используем перспективную проекцию, которая подразумевает так называемое «однородное деление» — после умножения вектора (Px, Py, Pz, 1) на матрицу проекции его компоненты следует разделить на компонент W этого вектора. После перехода в пространство проекции и однородного деления точка оказывается в NDC пространстве. NDC пространство представляет из себя набор из трех координат x, y, z, где x и y принадлежат [-1, 1], а z — [0,1] (Надо сказать, что в OpenGL параметры несколько иные).
     Теперь давайте приступим к решению нашей задачи. В моем случае пирамида расположена в видовом пространстве. Нам нужно шесть плоскостей, которые ее описывают (рис.17а). Плоскость можно описать с помощью нормали и точки, которая этой плоскости принадлежит. Сперва давайте получим точки — для этого возьмем следующий набор координат в NDC пространстве:
std::vector<Point4F> pointsN = {
{-1.0f, -1.0f, 0.0f, 1.0f}, {-1.0f, 1.0f, 0.0f, 1.0f},
{ 1.0f, 1.0f, 0.0f, 1.0f}, {1.0f, -1.0f, 0.0f, 1.0f},
{-1.0f, -1.0f, 1.0f, 1.0f}, {-1.0f, 1.0f, 1.0f, 1.0f},
{ 1.0f, 1.0f, 1.0f, 1.0f}, {1.0f, -1.0f, 1.0f, 1.0f}
};
Посмотрите, в первых четырех точках значение z равно 0 — это значит что они принадлежат ближней плоскости отсечения, в последних четырех z равно 1 — они принадлежат дальней плоскости отсечения. Теперь эти точки нужно преобразовать в видовое пространство. Но как?
Помните пример про космонавта — так вот тут тоже самое. Нам нужно умножить точки на обратную матрицу проекции. Правда, после этого нужно еще поделить каждый из них на его координату W. В результате мы получим нужные координаты (рис.17b). Давайте теперь разберемся с нормалями — они должны быть направлены внутрь пирамиды, поэтому нам надо выбрать необходимый порядок вычисления векторного произведения.
Matrix4x4 invProj = Matrix4x4::Inverse(camera->GetProjMatrix());
std::vector<Point3F> pointsV;
for(const Point4F &pN : pointsN){
Point4F pV = invProj.Transform(pN);
pV /= pV.w;
pointsV.push_back(Cast<Point3F>(pV));
}
planes[0] = {pointsV[0], pointsV[1], pointsV[2]}; //near plane
planes[1] = {pointsV[4], pointsV[5], pointsV[6]}; //far plane
planes[2] = {pointsV[0], pointsV[1], pointsV[4]}; //left plane
planes[3] = {pointsV[2], pointsV[3], pointsV[6]}; //right plane
planes[4] = {pointsV[1], pointsV[2], pointsV[6]}; //top plane
planes[5] = {pointsV[0], pointsV[3], pointsV[7]}; //bottom plane
planes[0].normal *= -1.0f;
planes[5].normal *= -1.0f;
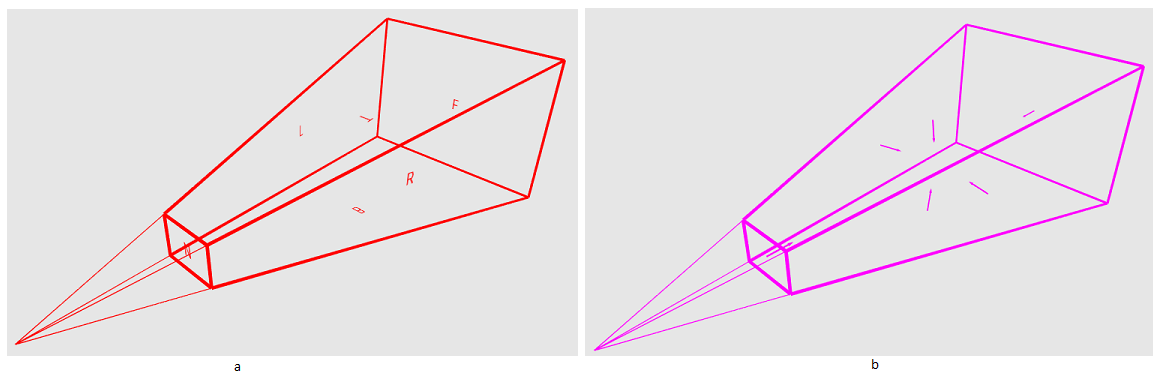
Рис.17 Пирамида видимости
Пирамида построена — настало время ее использовать. Те секторы, которые не попадают внутрь пирамиды, мы не рисуем. Для того, что бы определить, находится ли сектор внутри пирамиды видимости, мы будем проверять ограничивающую сферу, расположенную в центре этого сектора. Это не дает точных результатов, но в данном случае я не вижу ничего страшного в том, что будут нарисованы несколько лишних секторов. Радиус сферы вычисляется следующим образом:
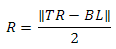
где TR — правый верхний угол сектора, BL — левый нижний угол. Так как все секторы имеют одинаковую площадь, то радиус достаточно вычислить один раз.
Как нам определить, находится ли сфера, описывающая сектор, внутри пирамиды видимости? Сперва нам нужно определить, пересекается ли сфера с плоскостьтю и если нет, то с какой стороны от нее она находится. Давайте получим вектор на центр сферы
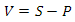
где P — точка на плоскости и S — центр сферы. Теперь вычислим скалярное произведение этого вектора на нормаль плоскости. Ориентацию можно определить с помошью знака скалярного произведения — как говорилось ранее, если он положительный, то сфера находится спереди от плоскости, если отрицательный, то сфера находится позади. Осталось определить, пересекает ли сфера плоскость. Давайте возьмем два вектора — N (вектор нормали) и V. Теперь построим вектор от N до V — назовем его K. Так вот, нам надо найти такую длину N, чтобы он с K образовывал угол 90 градусов (формально говоря, чтобы N и K были ортогональны). Оки доки, посмотрите на рис.18a — из свойств прямоугольного треугольника мы знаем, что
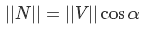
Нужно найти косинус. Используя ранее упомянутое свойство скалярного произведения
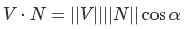
делим обе части на |V|*|N| и получаем
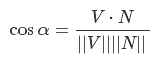
используем этот результат:
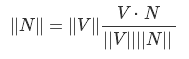
так как |V| это просто число, то можно сократить на |V|, и тогда мы получим
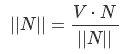
Так как вектор N нормализован, то последним шагом мы просто умножем его на получившееся значение, в противном случае вектор следует нормализовать — в этом случае конечное уравнение выглядит так:
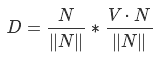
Где D это наш новый вектор. Этот процес называется «Векторная проекция»(рис.18b). Но зачем нам это? Мы знаем, что вектор определяется длиной и направлением и никак не меняется от его положения — это значит, что если мы расположим D так, чтобы он указывал на S, то его длина будет равна минимальному расстоянию от S до плоскости (рис.18с)
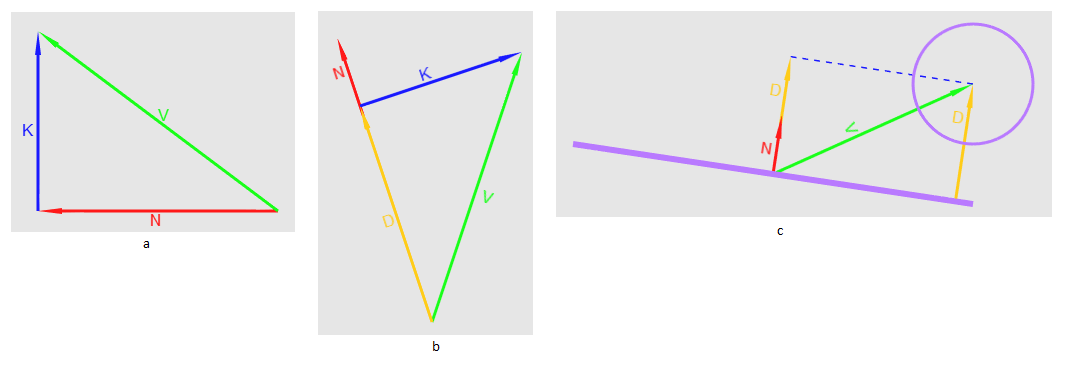
Рис.18 a Проекция N на V, b Наглядное отображение длины спроецированного N применительно к точке, с Наглядное отображение
длины спроецированного N применительно к сфере с центром в S
Так как у нас нет необходимости в спроецированном векторе, достаточно лишь вычислить его длину. Учитывая, что N это единичный вектор, нам нужно лишь вычислить скалярное произведение V на N. Собрав все воедино, мы можем наконец заключить, что сфера пересекает плоскость, если значение скалярного произведения вектора на центр сферы и нормали к плоскости больше нуля и меньше значения радиуса этой сферы.
Для того, чтобы утверждать, что сфера находится внутри пирамиды видимости, нам надо убедиться, что она либо пересекает одну из плоскостей, либо находится спереди от каждой из них. Можно поставить вопрос подругому — если сфера не пересекает и находится позади хотябы одной из плоскостей — она определенно вне пирамиды видимости. Так мы и сделаем. Обратите внимание, что я перевожу центр сферы в тоже пространство, в котором расположена пирамида — в пространство вида.
bool Frustum::TestSphere(const Point3F &Pos,
float Radius,
const Matrix4x4 &WorldViewMatrix) const
{
Point3F posV = WorldViewMatrix.Transform(Pos);
for(const Plane &pl : planes){
Vector3 toSphPos = posV - pl.pos;
if(Vector3::Dot(toSphPos, pl.normal) < -Radius)
return false;
}
return true;
}
10. Трещины
Еще одна проблема, которую нам предстоит решить — трещины на границах уровней детализации (рис.19).

Рис.19 демонстрация трещин ландшафта
В первую очередь нам надо определить те секторы, которые лежат на границе уровней детализации. На первый взгляд кажется, что это ресурсоемкая задача — ведь количество секторов на каждом из уровней постоянно меняется. Но если использовать данные смежности, то решение значительно упрощается. Что такое данные смежности? Смотрите, у каждого сектора есть четыре соседа. Набор ссылок на них — будь то указатели или индексы — и есть данные смежности. С их помощью мы легко определим, какой сектор лежит на границе — достаточно проверить, какому уровню принадлежат его соседи.
Ну что же, давайте найдем соседей каждого сектора. И опять же нам не нужно переберать в цикле все секторы. Представим, что мы работаем с сектором с координатами X и Y в пространстве сетки. Если он не касается ребра куба, то координаты его соседей будут такими:
Сосед сверху — (X, Y — 1)
Сосед снизу — (X, Y + 1)
Сосед слева — (X — 1, Y)
Сосед справа — (X + 1, Y)
Если же сектор касается ребра, то мы помещаем его специальный контейнер. После обработки всех шести граней в нем будут содержаться все граничные секторы куба. Вот в этом контейнере нам и предстоит осуществлять перебор. Заранее вычислим ребра для каждого сектора:
struct SectorEdges
{
CubeSectors::Sector *owner;
typedef std::pair<Point3F, Point3F> Edge;
Edge edges[4];
};
std::vector<SectorEdges> sectorsEdges;
//borderSectors - контейнер с граничными секторами
for(CubeSectors::Sector &sec : borderSectors){
// каждый сектор содержит два вектора, которые описывают грань куба,
// которой он принадлежит
Vector3 v1 = sec.vec1 * sec.sideSize;
Vector3 v2 = sec.vec2 * sec.sideSize;
//sec.startPos - начало сектора в локальном пространстве
SectorEdges secEdges;
secEdges.owner = &sec;
secEdges.edges[ADJ_BOTTOM] = {sec.startPos, sec.startPos + v1};
secEdges.edges[ADJ_LEFT] = {sec.startPos, sec.startPos + v2};
secEdges.edges[ADJ_TOP] = {sec.startPos + v2, sec.startPos + v2 + v1};
secEdges.edges[ADJ_RIGHT] = {sec.startPos + v1, sec.startPos + v2 + v1};
sectorsEdges.push_back(secEdges);
}
Далее идет сам перебор
for(SectorEdges &edgs : sectorsEdges)
for(size_t e = 0; e < 4; e++)
if(edgs.owner->adjacency[e] == nullptr)
FindSectorEdgeAdjacency(edgs, (AdjacencySide)e, sectorsEdges);
Функция FindSectorEdgeAdjacency() выглядит так
void CubeSectors::FindSectorEdgeAdjacency(SectorEdges &Sector,
CubeSectors::AdjacencySide Side,
std::vector<SectorEdges> &Neibs)
{
SectorEdges::Edge &e = Sector.edges[Side];
for(SectorEdges &edgs2 : Neibs){
if(edgs2.owner == Sector.owner)
continue;
for(size_t e = 0; e < 4; e++){
SectorEdges::Edge &e2 = edgs2.edges[e];
if((Math::Equals(e.first, e2.first) && Math::Equals(e.second, e2.second)) ||
(Math::Equals(e.second, e2.first) && Math::Equals(e.first, e2.second)))
{
Sector.owner->adjacency[Side] = edgs2.owner;
edgs2.owner->adjacency[e] = Sector.owner;
return;
}
}
}
}
Обратите внимание, что мы обновляем данные смежности для двух секторов — искомого (Sector) и найденного соседа
Теперь, используя полученные нами данные смежности, нам предстоит найти те ребра секторов, которые принадлежат границе уровней детализации. План такой — перед отрисовкой найдем граничные секторы. Затем для каждого сектора в Instance buffer помимо основной
информации запишем коэффициент тесселяции и четырехмерный вектор коэффициентов тесселяции для соседних секторов. Описание вершины теперь будет выглядеть так:
std::vector<D3D11_INPUT_ELEMENT_DESC> meta = {
//координаты в пространстве сетки
{"POSITION", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 0, D3D11_INPUT_PER_VERTEX_DATA, 0}
//первый вектор грани
{"TEXCOORD", 0, DXGI_FORMAT_R32G32B32_FLOAT, 1, 0,D3D11_INPUT_PER_INSTANCE_DATA, 1},
//второй вектор грани
{"TEXCOORD", 1, DXGI_FORMAT_R32G32B32_FLOAT, 1, 12, D3D11_INPUT_PER_INSTANCE_DATA, 1},
//начало грани
{"TEXCOORD", 2, DXGI_FORMAT_R32G32B32_FLOAT, 1, 24, D3D11_INPUT_PER_INSTANCE_DATA, 1},
//коэффициенты тесселяции соседних секторов
{"TEXCOORD", 3, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 36, D3D11_INPUT_PER_INSTANCE_DATA, 1},
//коэффициент тесселяции сектора
{"TEXCOORD", 4, DXGI_FORMAT_R32_FLOAT, 1, 52, D3D11_INPUT_PER_INSTANCE_DATA, 1}
}
После того, как мы распределили секторы по уровням детализации, определим соседние коэффициенты тесселяции для каждого сектора:
for(LodsStorage::Lod &lod : lods){
const std::vector<Sector*> §ors = lod.GetSectors();
bool lastLod = lod.GetInd() == lods.GetCount() - 1;
for(Sector *s : sectors){
int32_t tessFacor = s->GetTessFactor();
s->GetBorderTessFactor() = {
GetNeibTessFactor(s, Sector::ADJ_BOTTOM, tessFacor, lastLod),
GetNeibTessFactor(s, Sector::ADJ_LEFT, tessFacor, lastLod),
GetNeibTessFactor(s, Sector::ADJ_TOP, tessFacor, lastLod),
GetNeibTessFactor(s, Sector::ADJ_RIGHT, tessFacor, lastLod)
};
}
}
Функция, которая ищет соседний фактор тесселяции:
float Terrain::GetNeibTessFactor(Sector *Sec,
Sector::AdjacencySide Side,
int32_t TessFactor,
bool IsLastLod)
{
Sector *neib = Sec->GetAdjacency()[Side];
int32_t neibTessFactor = neib->GetTessFactor();
return (neibTessFactor < TessFactor) ? (float)neibTessFactor : 0.0f;
}
Если мы возвращаем ноль, то сосед на стороне Side не представляет для нас интерес. Забегу вперед и скажу, что нам нужно устранять трещины со стороны уровня с большим коэффициентом тесселяции.
Теперь передем к шейдеру. Напомню, что сперва нам нужно получить координаты сетки, используя координаты тесселятора. Затем эти координаты преобразуются в точку на грани куба, эта точка нормализуется — и вот мы имеем точку на сфере:
float3 p = Tri[0].netPos * Coord.x + Tri[1].netPos * Coord.y + Tri[2].netPos * Coord.z;
float3 planePos = Tri[0].startPos + Tri[0].vec1 * p.x * gridStep.x
+ Tri[0].vec2 * p.y * gridStep.y;
float3 sphPos = normalize(planePos);
Сперва нам надо выяснить, принадлежит ли вершина либо первой или последней строке сетки, либо первому или последнему столбцу — в этом случае вершина принадлежит ребру сектора. Но этого не достаточно — нам нужно определить, принадлежит ли вершина границе уровней детализации. Для этого используем информацию о соседних секторах, а точнее их уровни тесселяции:
float4 bTf = Tri[0].borderTessFactor;
bool isEdge = (bTf.x != 0.0f && p.y == 0.0f) || //bottom
(bTf.y != 0.0f && p.x == 0.0f) || //left
(bTf.z != 0.0f && p.y == gridSize.y) || //top
(bTf.w != 0.0f && p.x == gridSize.x) //right
Теперь главный этап — собственно, устранение трещин. Посмотрите на рис.20. Красная линия — грань вершины, принадлежащей второму уровню детализации. Две синие линии — грани третьего уровня детализации. Нам нужно, чтобы V3 принадлежала красной линии — то есть лежала на грани второго уровня. Как как высоты V1 и V2 равны для обоих уровней, V3 можно найти с помощью линейной интерполяции между ними
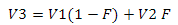
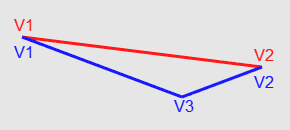
Рис.20 Демонстрация граней, которые образуют трещину, в виде линий
Пока мы не имеем ни V1 и V2, ни коэффициента F. Сначала нам нужно найти индекс точки V3. Тоесть если сетка имеет размер 32 на 32 и коэффициент тесселяции равен четырем, то этот индекс будет от нуля до 128 (32 * 4). У нас уже есть координаты в пространстве сетки p — в рамках данного примера они могут быть например (15.5, 16). Для получения индекса нужно умножить одну из координат p на коэффициент тесселяции. Нам также понадобится начало грани и направление на ее конец — один из углов сектора.
float edgeVertInd = 0.0f;
float3 edgeVec = float3(0.0f, 0.0f, 0.0f);
float3 startPos = float3(0.0f, 0.0f, 0.0f);
uint neibTessFactor = 0;
if(bTf.x != 0.0f && p.y == 0.0f){ // bottom
edgeVertInd = p.x * Tri[0].tessFactor;
edgeVec = Tri[0].vec1;
startPos = Tri[0].startPos;
neibTessFactor = (uint)Tri[0].borderTessFactor.x;
}else if(bTf.y != 0.0f && p.x == 0.0f){ // left
edgeVertInd = p.y * Tri[0].tessFactor;
edgeVec = Tri[0].vec2;
startPos = Tri[0].startPos;
neibTessFactor = (uint)Tri[0].borderTessFactor.y;
}else if(bTf.z != 0.0f && p.y == gridSize.y){ // top
edgeVertInd = p.x * Tri[0].tessFactor;
edgeVec = Tri[0].vec1;
startPos = Tri[0].startPos + Tri[0].vec2 * (gridStep.x * gridSize.x);
neibTessFactor = (uint)Tri[0].borderTessFactor.z;
}else if(bTf.w != 0.0f && p.x == gridSize.x){ // right
edgeVertInd = p.y * Tri[0].tessFactor;
edgeVec = Tri[0].vec2;
startPos = Tri[0].startPos + Tri[0].vec1 * (gridStep.x * gridSize.x);
neibTessFactor = (uint)Tri[0].borderTessFactor.w;
}
Далее нам нужно найти индексы для V1 и V2. Представтье что у вас есть число 3. Вам нужно найти два ближайших числа, кратных двум. Для этого вы вычисляете остаток от деления трех на два — он равен еденице. Затем вы вычитаете либо прибавляете этот остаток к трем и получаете нужный результат. Также с индексами, только вместо двух у нас будет соотношение коэффициентов тесселяции уровней детализации. Тоесть если у третьего уровня коэффициент равен 16, а у второго 2, то соотношение будет равно 8. Теперь, чтобы получить высоты, сперва надо получить соответствующие точки на сфере, нормализовав точки на грани. Начало и направление ребра мы уже подготовили — осталось вычислить длину вектора от V1 до V2. Так как длина ребра ячейки оригинальной сетки равна gridStep.x, то нужная нам длина равна gridStep.x / Tri[0].tessFactor. Затем по точкам на сфере мы получим высоту, как было рассказано ранее.
float GetNeibHeight(float3 EdgeStartPos, float3 EdgeVec, float VecLen, float3 NormOffset)
{
float3 neibPos = EdgeStartPos + EdgeVec * VecLen;
neibPos = normalize(neibPos);
return GetHeight(neibPos, NormOffset);
}
float vertOffset = gridStep.x / Tri[0].tessFactor;
uint tessRatio = (uint)tessFactor / (uint)neibTessFactor;
uint ind = (uint)edgeVertInd % tessRatio;
uint leftNeibInd = (uint)edgeVertInd - ind;
float leftNeibHeight = GetNeibHeight(startPos,
edgeVec,
vertOffset * leftNeibInd,
normOffset);
uint rightNeibInd = (uint)edgeVertInd + ind;
float rightNeibHeight = GetNeibHeight(startPos,
edgeVec,
vertOffset * rightNeibInd,
normOffset);
Ну и послендний компонент — фактор F. Его мы получим разделив остаток от деления на соотношение коэффициентов (ind) на соотношение коэффициентов (tessRatio)
float factor = (float)ind / (float)tessRatio;
Завершающий этап — линейная интерполяция высот и получение новой вершины
float avgHeight = lerp(leftNeibHeight, rightNeibHeight, factor);
posL = sphPos * (sphereRadius + avgHeight);
Также может появиться трещина в месте, где граничат секторы с текстурными координатами ребер равными 1 или 0. В этом случае я беру среднее значение между высотами для двух координат:
float GetHeight(float2 TexCoords)
{
float2 texCoords2 = TexCoords * texCoordsScale;
float mHeight = mainHeightTex.SampleLevel(mainHeightTexSampler, TexCoords, 0).x;
float dHeight = distHeightTex.SampleLevel(distHeightTexSampler, texCoords2, 0).x;
return (mHeight + dHeight) * maxTerrainHeight;
}
float GetHeight(float3 SphPos, float3 NormOffset)
{
float2 texCoords1 = GetTexCoords(SphPos, NormOffset);
float height = GetHeight(texCoords1);
if(texCoords1.x == 1.0f){
float height2 = GetHeight(float2(0.0f, texCoords1.y));
return lerp(height, height2, 0.5f);
}else if(texCoords1.x == 0.0f){
float height2 = GetHeight(float2(1.0f, texCoords1.y));
return lerp(height, height2, 0.5f);
}else
return height;
}
11. Обработка на GPU
Давайте перенесем обработку секторов на GPU. У нас будет два Compute шейдера — первый выполнит отсечение по пирамиде видимости и определит уровень детализации, второй получит граничные коэффициенты тесселяции для устранения трещин. Разделение на два этапа нужно потому, что как и в случае с CPU, мы не можем коректно определить соседей для секторов до тех пор, пока не произведем отсечение. Так как оба шейдера будут использовать данные уровней детализации и работать с секторами, я ввел две общих структуры: Sector и Lod
struct Sector
{
float3 vec1, vec2;
float3 startPos;
float3 normCenter;
int adjacency[4];
float borderTessFactor[4];
int lod;
};
struct Lod
{
RangeF dotRange;
float tessFactor;
float padding;
float4 color;
};
Мы будем использовать три основных буфера — входной(содержит изначальную информацию о секторах), промежуточный(в нем находятся данные секторов, полученных в результате работы первого этапа) и итоговый(Будет передаваться на отрисовку). Данные входного буфера не будут меняться, поэтому в поле Usage структуры D3D11_BUFFER_DESC разумно использовать значение D3D11_USAGE_IMMUTABLE Мы просто запишем в него данные всех секторов с единственной разницей, что для данных смежности мы будем использовать индексы секторов, а не указатели на них. Для индекса уровня детализации и граничных коэффициентов тесселяции установим нулевые значения:
static const size_t sectorSize = sizeof(Vector3) + //vec1
sizeof(Vector3) + //vec2
sizeof(Point3F) + //normCenter
sizeof(Point3F) + //startPos
sizeof(Point4) + //adjacency
sizeof(Vector4) + //borderTessFactor
sizeof(int32_t);//lod
size_t sectorsDataSize = sectors.GetSectors().size() * sectorSize;
std::vector<char> sectorsData(sectorsDataSize);
char* ptr = §orsData[0];
const Sector* firstPtr = §ors.GetSectors()[0];
for(const Sector &sec : sectors){
Utils::AddToStream<Vector3>(ptr, sec.GetVec1());
Utils::AddToStream<Vector3>(ptr, sec.GetVec2());
Utils::AddToStream<Point3F>(ptr, sec.GetStartPos());
Utils::AddToStream<Point3F>(ptr, sec.GetNormCenter());
Utils::AddToStream<int32_t>(ptr, sec.GetAdjacency()[0] - firstPtr);
Utils::AddToStream<int32_t>(ptr, sec.GetAdjacency()[1] - firstPtr);
Utils::AddToStream<int32_t>(ptr, sec.GetAdjacency()[2] - firstPtr);
Utils::AddToStream<int32_t>(ptr, sec.GetAdjacency()[3] - firstPtr);
Utils::AddToStream<Vector4>(ptr, Vector4());
Utils::AddToStream<int32_t>(ptr, 0);
}
inputData = Utils::DirectX::CreateBuffer(§orsData[0],//Raw data
sectorsDataSize,//Buffer size
D3D11_BIND_SHADER_RESOURCE,//bind flags
D3D11_USAGE_IMMUTABLE,//usage
0,//CPU access flags
D3D11_RESOURCE_MISC_BUFFER_STRUCTURED,//misc flags
sectorSize);//structure byte stride
Теперь пара слов о промежуточном буфере. Он будет играть две роли — выходного для первого шейдера и входного для второго, поэтому мы укажем в поле BindFlags значение D3D11_BIND_UNORDERED_ACCESS | D3D11_BIND_SHADER_RESOURCE. Также создадим для него два отображения — UnorderedAccessView, которое позволит шейдеру записывать в него результат работы и ShaderResourceView, с помощью которого мы будем использовать буфер как входной. Размер его будет таким же, как у ранее созданного входного буфера
UINT miscFlags = D3D11_BIND_UNORDERED_ACCESS | D3D11_BIND_SHADER_RESOURCE;
intermediateData = Utils::DirectX::CreateBuffer(
sectors.GetSectors().size() * sectorSize,//Buffer size
miscFlags,
D3D11_USAGE_DEFAULT,//usage
0,//CPU access flags
D3D11_RESOURCE_MISC_BUFFER_STRUCTURED,//misc flags
sectorSize);//structure byte stride
intermediateUAW = Utils::DirectX::CreateUnorderedAccessView(
intermediateData,
D3D11_BUFFER_UAV{0, sectors.GetSectors().size(), 0});
intermediateSRV = Utils::DirectX::CreateShaderResourceView(
intermediateData,
D3D11_BUFFEREX_SRV{0, sectors.GetSectors().size(), 0});
Далее я приведу основную функцию первого шейдера:
StructuredBuffer<Sector> inputData : register(t0);
RWStructuredBuffer<Sector> outputData : register(u0);
[numthreads(1, 1, 1)]
void Process( int3 TId : SV_DispatchThreadID )
{
int ind = TId.x;
Sector sector = inputData[ind];
float dotVal = dot(toWorldPos, sector.normCenter);
if(dotVal < dotRange.minVal || dotVal > dotRange.maxVal){
outputData[ind] = sector;
return;
}
if(!IsVisible(sector.normCenter)){
outputData[ind] = sector;
return;
}
for(int l = 0; l < 4; l++){
Lod lod = lods[l];
if(dotVal >= lod.dotRange.minVal && dotVal <= lod.dotRange.maxVal)
sector.lod = l + 1;
}
outputData[ind] = sector;
}
После вычисления скалярного произведения мы проверяем, находится ли сектор в потенциально видимой области. Далее мы уточняем факт его видимости с помощью вызова IsVisible(), который идентичен вызову Frustum::TestSphere(), показанному ранее. Работа функции зависит от переменных worldView, sphereRadius, frustumPlanesPosV и frustumPlanesNormalsV, значения для которых нужно передать в шейдер заранее. Далее мы определяем уровень детализации. Обратите внимание, что индекс уровня мы указываем от еденицы — это нужно для того, чтобы на втором этапе отбросить те секторы, уровень детализации которых равен нулю.
Теперь нам нужно подготовить буферы для второго этапа. Мы хотим использовать буфер, как выходной у Compute шейдера и входной для тесселятора — для этого нам нужно указать в поле BindFlags значение D3D11_BIND_UNORDERED_ACCESS | D3D11_BIND_VERTEX_BUFFER. Нам придется работать с данными буфера напрямую, поэтому укажем в поле MiscFlags значение D3D11_RESOURCE_MISC_BUFFER_ALLOW_RAW_VIEWS Для отображения такого буфера мы будем использовать значение DXGI_FORMAT_R32_TYPELESS в поле Flags, а в поле NumElements укажем всего буфера, деленный на четыре
size_t instancesByteSize = instanceByteSize * sectors.GetSectors().size();
outputData = Utils::DirectX::CreateBuffer(instancesByteSize,
D3D11_BIND_UNORDERED_ACCESS | D3D11_BIND_VERTEX_BUFFER,
D3D11_USAGE_DEFAULT,
0,
D3D11_RESOURCE_MISC_BUFFER_ALLOW_RAW_VIEWS,
0);
D3D11_BUFFER_UAV uavParams = {0, instancesByteSize / 4, D3D11_BUFFER_UAV_FLAG_RAW};
outputUAW = Utils::DirectX::CreateUnorderedAccessView(outputData,
uavParams,
DXGI_FORMAT_R32_TYPELESS);
Нам также потребуется счетчик. С его помощью мы осуществим адресацию памяти в шейдере и используем его конечное значение в аргументе instanceCount вызова DrawIndexedInstanced(). Счетчик я реализовал в виде буфера размером 16 байтов. Также при создании отображения в поле Flags поля D3D11_BUFFER_UAV я использовал значение D3D11_BUFFER_UAV_FLAG_COUNTER
counter = Utils::DirectX::CreateBuffer(sizeof(UINT),
D3D11_BIND_UNORDERED_ACCESS,
D3D11_USAGE_DEFAULT,
0,
D3D11_RESOURCE_MISC_BUFFER_STRUCTURED,
4);
D3D11_BUFFER_UAV uavParams = {0, 1, D3D11_BUFFER_UAV_FLAG_COUNTER};
counterUAW = Utils::DirectX::CreateUnorderedAccessView(counter, uavParams);
Настало время привести код второго шейдера
StructuredBuffer<Sector> inputData : register(t0);
RWByteAddressBuffer outputData : register(u0);
RWStructuredBuffer<uint> counter : register(u1);
[numthreads(1, 1, 1)]
void Process( int3 TId : SV_DispatchThreadID )
{
int ind = TId.x;
Sector sector = inputData[ind];
if(sector.lod != 0){
sector.borderTessFactor[0] = GetNeibTessFactor(sector, 0); //Bottom
sector.borderTessFactor[1] = GetNeibTessFactor(sector, 1); //Left
sector.borderTessFactor[2] = GetNeibTessFactor(sector, 2); //Top
sector.borderTessFactor[3] = GetNeibTessFactor(sector, 3); //Right
int c = counter.IncrementCounter();
int dataSize = 56;
outputData.Store(c * dataSize + 0, asuint(sector.startPos.x));
outputData.Store(c * dataSize + 4, asuint(sector.startPos.y));
outputData.Store(c * dataSize + 8, asuint(sector.startPos.z));
outputData.Store(c * dataSize + 12, asuint(sector.vec1.x));
outputData.Store(c * dataSize + 16, asuint(sector.vec1.y));
outputData.Store(c * dataSize + 20, asuint(sector.vec1.z));
outputData.Store(c * dataSize + 24, asuint(sector.vec2.x));
outputData.Store(c * dataSize + 28, asuint(sector.vec2.y));
outputData.Store(c * dataSize + 32, asuint(sector.vec2.z));
outputData.Store(c * dataSize + 36, asuint(sector.borderTessFactor[0]));
outputData.Store(c * dataSize + 40, asuint(sector.borderTessFactor[1]));
outputData.Store(c * dataSize + 44, asuint(sector.borderTessFactor[2]));
outputData.Store(c * dataSize + 48, asuint(sector.borderTessFactor[3]));
outputData.Store(c * dataSize + 52, asuint(sector.lod));
}
}
Код функции GetNeibTessFactor() практически идентичен ее CPU аналогу. Единственное различие в том, что мы используем индексы соседей а не указатели на них. Буфер outputData имеет тип RWByteAddressBuffer, поэтому для работы с ним мы используем метод Store(in uint address, in uint value). Значение переменной dataSize равно размеру данных вершины с классом D3D11_INPUT_PER_INSTANCE_DATA, Описание вершины можно посмотреть в разделе 10. В общем это традиционная для C/С++ работа с указателями. После выполнения двух шейдеров мы можем использовать outputData как InstanceBuffer. Процесс отрисовки выглядит так
Utils::DirectX::SetPrimitiveStream({vb, outputData},
ib,
{vertexSize, instanceByteSize},
D3D11_PRIMITIVE_TOPOLOGY_3_CONTROL_POINT_PATCHLIST);
DeviceKeeper::GetDeviceContext()->CopyStructureCount(indirectArgs, 4, counterUAW);
Shaders::Apply(terrainShaders, [&]()
{
DeviceKeeper::GetDeviceContext()->DrawIndexedInstancedIndirect(indirectArgs, 0);
});
Utils::DirectX::SetPrimitiveStream({nullptr, nullptr}, nullptr, {0, 0});
За более подробной информацией о методах DrawIndexedInstancedIndirect() и CopyStructureCount() обращайтесь к приложению 2
12. Камера
Наверняка вам известно, как помтроить модель простой FPS(First Person Shooter) камеры. Я действую по такому сценарию:
- 1. Из двух углов получаю вектор направления
- 2. с помошью вектора направления и вектора (0, 1, 0) получаю базис
- 3. согласно вектору направления и вактору вправо, полученному в п.2 изменяю позицию камеры
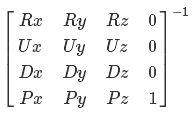
В нашем случае ситуация несколько осложняется — во первых мы должны двигаться относительно центра планеты, во вторых, при построении базиса вместо вектора (0, 1, 0) мы должны использовать нормаль сферы в точке, которой сейчас находимся. Чтобы достичь желаемых результатов, я буду использовать два базиса. Согласно первому будет изменяться позиция, второй будет описывать ориентацию камеры. Базисы взаимозависимы, но первым я вычисляю базис позиции, поэтому начну с него. Предположим, что у нас есть начальный базис позиции (pDir, pUp, pRight) и вектор направления vDir, по которому мы хотим продвинуться на некоторое расстояние. Прежде всего нам надо вычислить проекции vDir на pDir и pRight. Сложив их, мы получим обновленный вектор направления (рис.21).
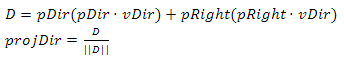
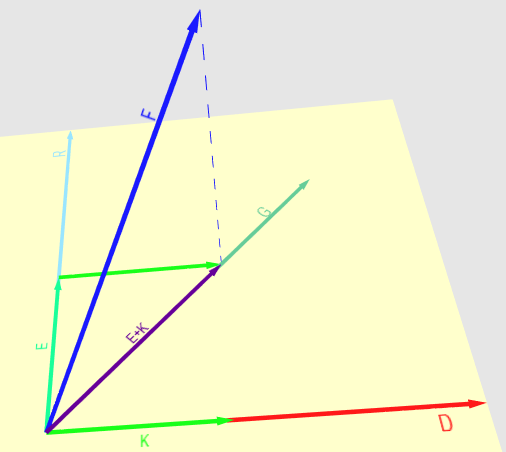
Рис.21 Наглядный процесс получения projDir
Далее мы движемся по этому вектору
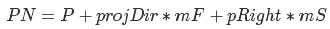
где P это позиция камеры, mF и mS — коэффициенты, означающе на сколько нам нужно продвинуться вперед либо вбок.
Мы не можем использовать PN как новую позицию камеры, потому что PN не принадлежит сфере. Вместо этого мы находим нормаль сферы в точке PN, и эта нормаль будет являться новым значением вектора вверх. Теперь мы можем сформировать обновленный базис
Vector3 nUp = Vector3::Normalize(PN - spherePos);
Vector3 nDir = projDir
Vector3 nRight = Vector3::Normalize(Vector3::Cross(pUp, pDir))
где spherePos — центр сферы.
Нам надо сделать так, чтобы каждый из его векторов был ортогональным по отношению к двум другим. Согласно свойству векторного произведения nRight удовлетворяет этому условию. Осталось добиться тогоже для nUp и nDir. Для этого спроецируем nDir на nUp и отнимим получившийся вектор от nDir (рис.22)
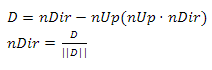
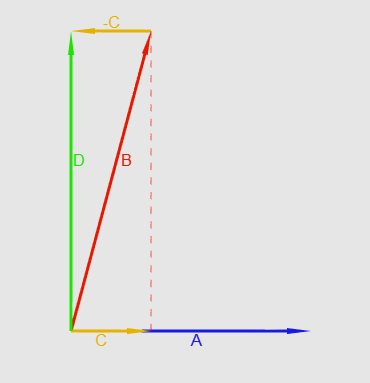
Рис.22 Ортогонализация nDir по отношению к nUp
Мы могли бы проделать тоже самое с nUp, но тогда он бы изменил свое направление, что в нашем случае неприемлимо. Теперь нормализуем nDir и получим обновленный ортонормированный базис направления
Вторым ключевым этапом является построение базиса ориентации. Основную сложность представляет получение вектора направления. наиболее подходящее решение — перевести точку с полярным углом a, азимутным углом b и расстоянием от начала координат равным единице из сферических координат в декартовые. Только если мы осуществим такой переход для точки с полярным углом равным нулю, то получим вектор, смотрящий вверх. Нам это не совсем подходит, так как мы будем инкрементировать углы и предполагаем, что такой вектор будет смотреть вперед. Банальное смещение угла на 90 градусов решит проблему, но более элегантно будет воспользоваться правилом смещения угла, которое гласит, что
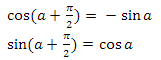
так и сделаем. В итоге у нас выходит следующее
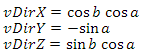
где a — полярный угол, b — азимутный угол.
Этот результат нам не совсем подходит — нам нужно построить вектор направления относительно базиса позиции. Давайте перепишем уравнение для vDir:
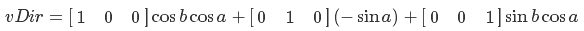
Все, как у космонавтов — по этому направлению столько, по тому столько. Теперь должно быть очевидно, что если мы заменим векторы стандартного базиса на pDir, pUp и pRight, то получим нужное нам направление. Вот так
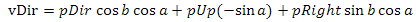
Можно представить тоже самое в виде матричного умножения
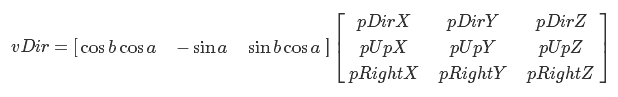
Вектор vUp изначально будет равен pUp. Вычислив векторное произведение vUp и vDir, мы получим vRight
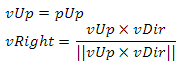
Теперь мы сделаем так, что бы vUp был ортогональным по отношению к остальным векторам базиса. Принцип тот же, что и при работе с nDir
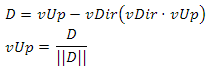
С базисами разобрались — осталось вычислить позицию камеры. Это делается так
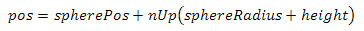
где spherePos — центр сферы, sphereRadius — радиус сферы и height — высота над поверхностью сферы. Приведу код работы описанной камеры:
float moveFactor = 0.0f, sideFactor = 0.0f, heightFactor = 0.0f;
DirectInput::GetInsance()->ProcessKeyboardDown({
{DIK_W, [&](){moveFactor = 1.0f;}},
{DIK_S, [&](){moveFactor = -1.0f;}},
{DIK_D, [&](){sideFactor = 1.0f;}},
{DIK_A, [&](){sideFactor = -1.0f;}},
{DIK_Q, [&](){heightFactor = 1.0f;}},
{DIK_E, [&](){heightFactor = -1.0f;}}
});
if(moveFactor != 0.0f || sideFactor != 0.0f){
Vector3 newDir = Vector3::Normalize(pDir * Vector3::Dot(pDir, vDir) +
pRight * Vector3::Dot(pRight, vDir));
Point3F newPos = pos + (newDir * moveFactor + pRight * sideFactor) * Tf * speed;
pDir = newDir;
pUp = Vector3::Normalize(newPos - spherePos);
pRight = Vector3::Normalize(Vector3::Cross(pUp, pDir));
pDir = Vector3::Normalize(pDir - pUp * Vector3::Dot(pUp, pDir));
pos = spherePos + pUp * (sphereRadius + height);
angles.x = 0.0f;
}
if(heightFactor != 0.0f){
height = Math::Saturate(height + heightFactor * Tf * speed, heightRange);
pos = spherePos + pUp * (sphereRadius + height);
}
DirectInput::MouseState mState = DirectInput::GetInsance()->GetMouseDelta();
if(mState.x != 0 || mState.y != 0 || moveFactor != 0.0f || sideFactor != 0.0f){
if(mState.x != 0)
angles.x = angles.x + mState.x / 80.0f;
if(mState.y != 0)
angles.y = Math::Saturate(angles.y + mState.y / 80.0f,
RangeF(-Pi * 0.499f, Pi * 0.499f));
vDir = Vector3::Normalize(pRight * sinf(angles.x) * cosf(angles.y) +
pUp * -sinf(angles.y) +
pDir * cosf(angles.x) * cosf(angles.y));
vUp = pUp;
vRight = Vector3::Normalize(Vector3::Cross(vUp, vDir));
vUp = Vector3::Normalize(vUp - vDir * Vector3::Dot(vDir, vUp));
}
viewMatrix = Matrix4x4::Inverse({{vRight, 0.0f},
{vUp, 0.0f},
{vDir, 0.0f},
{pos, 1.0f}});
Обратите внимание, что мы обнуляем angles.x после того, как обновили базис позиции. Это критически важно. Давайте представим, что мы одновременно изменяем угол обзора и перемещаемся по сфере. Сперва мы спроецируем вектор направления на pDir и pRight, получим смещение (newPos) и на его основе обновим базис позиции. Также сработает второе условие, и мы начнем обновлять базис ориентации. Но так как pDir и pRight уже был изменены в зависимости от vDir, то без сброса азимутного угла (angles.x) поворот будет более «крутым»
Заключение
Я благодарю читателя за проявленный интерес к статье. Надеюсь, что информация, в ней изложенная, была ему доступна, интересна и полезна. Предложения и замечания можете присылать мне по почте aliexwin32@mail.ru или оставлять в виде комментариев.
Желаю вам успеха!
UINT colorsRate = 99 / 3;
std::vector<D3D11_INPUT_ELEMENT_DESC> meta = {
{"POSITION", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 0, D3D11_INPUT_PER_VERTEX_DATA, 0},
{"NORMAL", 0, DXGI_FORMAT_R32G32B32_FLOAT, 0, 12, D3D11_INPUT_PER_VERTEX_DATA, 0},
{"TEXCOORD", 0, DXGI_FORMAT_R32G32_FLOAT, 0, 24, D3D11_INPUT_PER_VERTEX_DATA, 0},
{"WORLD", 0, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 0, D3D11_INPUT_PER_INSTANCE_DATA, 1},
{"WORLD", 1, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 16, D3D11_INPUT_PER_INSTANCE_DATA, 1},
{"WORLD", 2, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 32, D3D11_INPUT_PER_INSTANCE_DATA, 1},
{"WORLD", 3, DXGI_FORMAT_R32G32B32A32_FLOAT, 1, 48, D3D11_INPUT_PER_INSTANCE_DATA, 1},
{"COLOR", 0, DXGI_FORMAT_R32G32B32A32_FLOAT, 2, 0, D3D11_INPUT_PER_INSTANCE_DATA, colorsRate},
};
Обратите внимание, что вершина собирается из трех источников, причем данные последнего обновляются раз в 33 «инстанса». В итоге мы получим 33 инстанса первого цвета, еще 33 — второго и т.д. Теперь создадим буферы. Причем, так как цвета не будут меняться, буфер с цветами можем создать c флагом D3D11_USAGE_IMMUTABLE. Это значит, что после того как буфер будет инициализирован, только GPU будет иметь доступ к его данным, при чем только для чтения. Вот код создания буферов:
matricesTb = Utils::DirectX::CreateBuffer(sizeof(Matrix4x4) * 99,
D3D11_BIND_VERTEX_BUFFER,
D3D11_USAGE_DYNAMIC,
D3D11_CPU_ACCESS_WRITE);
colorsTb = Utils::DirectX::CreateBuffer(colors,
D3D11_BIND_VERTEX_BUFFER,
D3D11_USAGE_IMMUTABLE,
0);
далее по надобности обновляем буфер с матрицами(я использую функции своей библиотеки — надеюсь, что все будет ясно)
Utils::DirectX::Map<Matrix4x4>(matricesTb, [&](Matrix4x4 *Data)
{
//сначала записываем в буфер данные для шаров первого цвета
//затем для второго и т.д. Обратите внимание, что нужное соответсвие
//данных цветам нужно обеспечить на этапе формирования данных буфера
});
Доступ к данным в шейдере можно реализовать также, как я описал ранее
//indicesCnt - кол-во индексов, которое мы хотим отобразить
//instancesCnt - кол-во "инстансев", которое мы хотим отобразить
std::vector<UINT> args =
{
indicesCnt, //IndexCountPerInstance
instancesCnt,//InstanceCount
0,//StartIndexLocation
0,//BaseVertexLocation
0//StartInstanceLocation
};
D3D11_BUFFER_DESC bd = {};
bd.Usage = D3D11_USAGE_DEFAULT;
bd.ByteWidth = sizeof(UINT) * args.size();
bd.BindFlags = 0;
bd.CPUAccessFlags = 0;
bd.MiscFlags = D3D11_RESOURCE_MISC_DRAWINDIRECT_ARGS;
bd.StructureByteStride = 0;
ID3D11Buffer* buffer;
D3D11_SUBRESOURCE_DATA initData = {};
initData.pSysMem = &args[0];
HR(DeviceKeeper::GetDevice()->CreateBuffer(&bd, &initData, &buffer));
пример вызова DrawIndexedInstancedIndirect():
DeviceKeeper::GetDeviceContext()->DrawIndexedInstancedIndirect(indirectArgs, 0);
вторым аргументом мы передаем смещение в байтах от начала буфера, с которого нужно начинать читать данные. Как это можно использовать? Например, при реализации отсечения невидимой геометрии на GPU. В общем хронология такая — сперва в Compute шейдере мы заполняем AppendStructuredBuffer, который содержит данные видимой геометрии. Затем с помощью CopyStructureCount() мы устанавливаем значение количества «инстансев», которые хотим отбразить равным количеству записей в этом буфере и вызываем DrawIndexedInstancedIndirect()
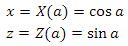
Теперь нам нужно для каждой функции вычислить производную. По сути, производная функции в заданной точке равна скорости изменения значений функции именно в этой точке. Согласно правилам дифференцирования тригонометрических функций:
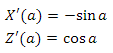
что в итоге дает нам тот же результат:
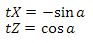
Почему мы можем использовать значения скорости как компоненты вектора направления? Я понимаю это так. Представьте, что у нас есть векторная функция (для t >= 0):
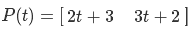
Вычислим производную для координаты X
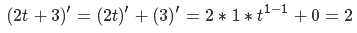
Теперь для Y
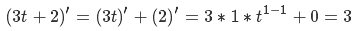
у нас получилось, что вектор скорости равен (2, 3), теперь найдем начальную точку
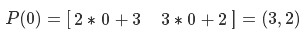
в итоге функцию P(t) мы можем выразить так:
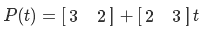
что простыми словами можно описать как «точка двигается от начала с координатами (3, 2) на t по направлению (2, 3)». Теперь давайте другой пример:
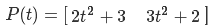
Снова вычислим производную для координаты X
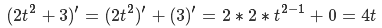
И для координаты Y
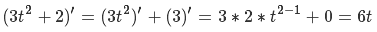
Теперь вектор скорости меняется в зависимости от аргумента. В этому случае простыми словами ситуацию можно описать так: «Точка движется от начала с координатами (3, 2), и направление ее движения постоянно меняется».
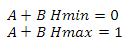
я получил
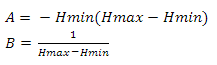
в результате этого функция F приобретает вид
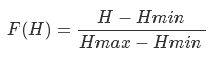
Теперь нам нужна функция, которая принимает коэффициент высоты от 0 до 1 и возвращает минимальное значение для скалярного произведения. Нам надо учесть, что чем ближе наблюдатель к поверхности — тем оно больше. Получается следующее уравнение:
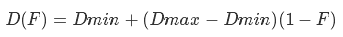
Раскроем скобки
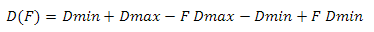
Упростим и получим
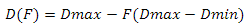
Теперь выразим D(F(H)) и получим
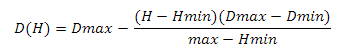
Автор: AlexWIN32