Функциональное программирование и c++ на практике

Функциональное программирование (далее ФП) нынче в моде. Статьи, книги, блоги. На каждой конференции обязательно присутствуют выступления, где люди рассказывают о красоте и удобстве функционального подхода. Я долгое время смотрел в его сторону издалека, но пришла пора попробовать применить его на практике. Прочитав достаточное количество теории и сложив в голове общую картину я решил написать небольшое приложение в функциональном стиле. Так как в данный момент я c++ программист, то буду использовать этот замечательный язык. За основу я возьму код из моей предыдущей статьи, т.е. моим примером будет упрощенная 2Д симуляция физических тел.

Заявление

Я ни в коем случае ни эксперт. Моей целью была попытка понять ФП и область его применения. В статье я шаг за шагом опишу как я превращал ООП код в некое подобие функционального с использованием c++. Из функциональных языков программирования я имел опыт только с Erlang. Другими словами, здесь я опишу процесс своего обучения — возможно, кому-то это поможет. И конечно же я приветствую конструктивную критику и замечания. Даже настаиваю, чтобы вы оставляли комментарии — что я делал неправильно, что можно улучшить.

Введение

В статье я не буду рассказывать теорию ФП — в сети великое множество материала, в том числе и на хабре. Хоть я и старался приблизить программу к чистому ФП, на 100% мне это сделать не удалось. В некоторых случаях из-за нецелесообразности, в некоторых — из-за отсутствия опыта. Так, например, рендер выполнен в привычном ООП стиле. Почему? Потому что одним из принципов ФП является неизменность данных (immutable data) и отсутствие состояния. Но для DirectX (API, который я использую) необходимо хранить буферы, текстуры, устройства. Конечно возможно создавать все заново каждый фрейм, но это будет чертовски долго (о производительности мы поговорим в конце статьи). Еще пример — в ФП часто применяются ленивые вычисления (lazy evaluation). Но я не нашел в программе места для их использования, поэтому их вы не встретите.

Main

Исходный код находится в этом коммите.

Все начинается в функции main() — здесь мы создаем фигуры (struct Shape) и запускаем бесконечный цикл, где будем обновлять симуляцию. Сразу стоит обратить внимание на оформление кода — я пишу функцию в отдельном cpp файле и в месте использования объявляю ее как extern — таким образом мне не нужно создавать отдельный заголовочный файл или даже отдельный тип, что положительно сказывается на времени компиляции и в целом делает код более читабельным: одна функция — один файл.

Итак, в главной функции мы создали набор данных и теперь нам нужно передать его далее — в функцию updateSimulation().

Update Simulation

Это сердце нашей программы и именно та часть, к которой применялось ФП. Сигнатура выглядит следующим образом:

vector<Shape> updateSimulation(float const dt, vector<Shape> const shapes, float const width, float const height);

Мы принимаем копию исходных данных и возвращаем новый вектор с измененными данными. Но почему копию, а не константную ссылку? Ведь выше я писал, что одним из принципов ФП является неизменность данных и const reference гарантирует это. Это так, но следующим важнейшим принципом является чистота функций (pure function) — т.е. отсутствие побочных эффектов и гарантия того, что функция будет возвращать одинаковые значения при одинаковых входных данных. Но, получая ссылку, мы этого гарантировать не можем. Разберем на примере. Допустим мы имеем некоторую функцию, принимающую константную ссылку:

int foo(vector<int> const & data)
{
    return accumulate(data.begin(), data.end(), 0);
}

И вызываем так:

vector<int> data{1, 1, 1};
int result{foo(data)};

Хотя foo() и принимает const &, сами данные не являются константными, а это значит, что они могут быть изменены до и в момент вызова accumulate(), например, другим потоком. Именно поэтому все данные должны приходить в виде копии.

Кроме того, чтобы поддержать принцип неизменности данных все поля всех пользовательских типов должны быть константами. Так выглядит, например, класс вектора:

struct Vec2
{
	float const x;
	float const y;

	Vec2(float const x = 0.0f, float const y = 0.0f) : x{ x }, y{ y }
	{}

	// member functions
}

Как видите, состояние задается при создании объекта и не меняется никогда! Т.е. даже состоянием назвать это можно с натяжкой — просто набор данных.

Вернемся к нашей функции updateSimulation(). Вызывается она следующим образом:

shapes = updateSimulation(dtStep, move(shapes), wSize.x, wSize.y);

Здесь используется семантика перемещения (std::move()) — это позволяет избавиться от лишних копий. В нашем случае, однако, это не имеет никакого эффекта, т.к. мы оперируем примитивными типами и перемещение эквивалентно копированию.

Есть еще интересный момент — наша функция возвращает новый набор данных, который мы присваиваем старой переменной shapes, что, по сути, является нарушением принципа отсутствия состояния. Однако я считаю, что локальную переменную мы можем менять безбоязненно — на результат функции это не повлияет, т.к. это изменение остается инкапсулированным внутри этой функции.

Тело функции выглядит так:

vector<Shape> updateSimulation(float const dt, vector<Shape> const shapes, float const width, float const height)
{
	// step 1 - update calculate current positions
	vector<Shape> const updatedShapes1{ calculatePositionsAndBounds(dt, move(shapes)) };

	// step 2 - for each shape calculate cells it fits in
	uint32_t rows;
	uint32_t columns;
	tie(rows, columns) = getNumberOfCells(width, height); // auto [rows, columns] = getNumberOfCells(width, height); - c++17 structured bindings - not supported in vs2017 at the moment of writing

	vector<Shape> const updatedShapes2{ calculateCellsRanges(width, height, rows, columns, move(updatedShapes1)) };

	// step 3 - put shapes in corresponding cells
	vector<vector<Shape>> const cellsWithShapes{ fillGrid(width, height, rows, columns, updatedShapes2) };

	// step 4 - calculate collisions
	vector<VelocityAfterImpact> const velocityAfterImpact{ solveCollisions(move(cellsWithShapes), columns) };

	// step 5- apply velocities
	vector<Shape> const updatedShapes3{ applyVelocities(move(updatedShapes2), velocityAfterImpact) };

	return updatedShapes3;
}

Здесь мы снова принимаем копии данных и возвращаем копию измененных данных. По моему мнению код выглядит очень наглядно и легок для понимания — здесь мы вызываем функцию за функцией, передавая измененные данные наподобие конвейера.

Далее я опишу сам алгоритм симуляции и как мне пришлось модифицировать его, чтобы вписаться в функциональный стиль, но без формул. Поэтому должно быть интересно.

Сalculate Positions And Bounds

Еще одна чистая функция, которая работает с копией данных и возвращает новые. Выглядит следующим образом:

vector<Shape> calculatePositionsAndBounds(float const dt, vector<Shape> const shapes)
{
	vector<Shape> updatedShapes;
	updatedShapes.reserve(shapes.size());

	for_each(shapes.begin(), shapes.end(), [dt, &updatedShapes](Shape const shape)
	{
		Shape const newShape{ shape.id, shape.vertices, calculatePosition(shape, dt), shape.velocity, shape.bounds, shape.cellsRange, shape.color, shape.massInverse };
		updatedShapes.emplace_back(newShape.id, newShape.vertices, newShape.position, newShape.velocity, calculateBounds(newShape), newShape.cellsRange, newShape.color, newShape.massInverse);
	});

	return updatedShapes;
}

Стандартная библиотека уже много лет поддерживает ФП. Алгоритм for_each — это функция высшего порядка, т.е. функция, принимающая другие функции. Вообще stl очень богат на алгоритмы, поэтому знание библиотеки очень важно, если вы пишите в функциональном стиле.

В приведенном коде есть пара интересных моментов. Первый — это ссылка на вектор в списке захвата лямбды. Да, я старался обойтись без ссылок совсем, но в данном месте это просто необходимо. И, как я писал выше, это не должно нарушать принципов, т.к. ссылка берется на локальный вектор, т.е. закрытый для внешнего мира. Здесь можно было бы обойтись без нее, используя цикл for, но я пошел в сторону наглядности и читабельности.

Второй момент связан с самим циклом. Опять же, так как не должно быть состояний, то и циклов быть не должно — ведь счетчик цикла и есть состояние. В чистом ФП циклов нет, их заменяет рекурсия. Давайте попробуем переписать функцию с ее использованием:

vector<Shape> updateOne(float const dt, vector<Shape> shapes, vector<Shape> updatedShapes)
{
	if (shapes.size() > 0)
	{
		Shape shape{ shapes.back() };
		shapes.pop_back();

		Shape const newShape{ shape.id, shape.vertices, calculatePosition(shape, dt), shape.velocity, shape.bounds, shape.cellsRange, shape.color, shape.massInverse };
		updatedShapes.emplace_back(newShape.id, newShape.vertices, newShape.position, newShape.velocity, calculateBounds(newShape), newShape.cellsRange, newShape.color, newShape.massInverse);
	}
	else
	{
		return updatedShapes;
	}

	return updateOne(dt, move(shapes), move(updatedShapes));
}

vector<Shape> calculatePositionsAndBounds(float const dt, vector<Shape> const shapes)
{
	return updateOne(dt, move(shapes), {});
}

Мы избавились от ссылок! Но вместо одной функции получилось две. И, что самое главное, ухудшилась читабельность (по крайней мере, для меня — человека выросшего на традиционном ООП). Интересный момент — здесь используется так называемая хвостовая рекурсия (tail recursion) — в теории в этом случае стэк должен очищаться. Однако, я не нашел в стандарте c++ записей о таком поведении, поэтому я не могу гарантировать отсутствие переполнения стэка (stack overflow). Учитывая все вышесказанное я решил остановиться на циклах и больше рекурсию в этой статье вы не увидите.

Calculate Cells Ranges и Fill Grid

Для ускорения расчетов я использую 2Д сетку, разделенную на ячейки. Находясь в этой сетке, объект может занимать несколько ячеек, как показано на картинке:

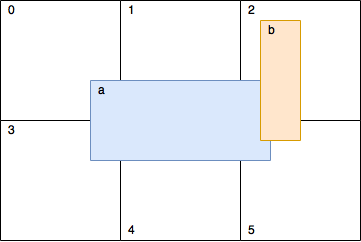
Функция calculateCellsRanges() рассчитывает ячейки, занимаемые фигурой, и возвращает измененные данные.

В функции fillGrid() мы наполняем каждую ячейку (в нашем примере ячейка — это просто std::vector) соответствующими фигурами. Т.е. если ячейка не содержит ничего, вернется пустой вектор. Позже в коде мы будем пробегать по каждой ячейке, и проверять внутри нее каждую фигуру с каждой другой на пересечение. Но на рисунке можно увидеть, что фигура a и фигура b находятся (помимо других ячеек) как в ячейке 2, так и в ячейке 5. Это значит, что проверка будет осуществляться дважды. Поэтому мы добавим логику, которая скажет — нужна ли проверка. Зная строки и столбцы сделать это тривиально.

Solve Collisions

В моей предыдущей статье я использовал следующую технику — если оказалось, что объекты накладывались, мы отодвигали их друг от друга.

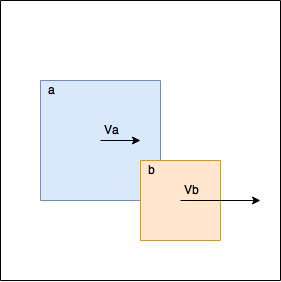
Т.е. мы делали так, чтобы объекты a и b переставали соприкасаться. Это добавляло много сложностей — нужно было заново рассчитывать bounding box каждый раз когда мы двигали объект. Чтобы избежать многократной перестановки мы ввели специальный аккумулятор, в который складывали все перестановки и позднее применяли этот аккумулятор только один раз. Так или иначе, пришлось ввести мьютексы для синхронизации, код был сложен и в таком виде не годился для функционального подхода. В новой попытке мы не будем перемещать объекты совсем, кроме того, мы будем производить рассчеты, только если они действительно необходимы. На картинке, например, рассчеты не нужны, т.к. фигура b движется быстрее фигуры a, т.е. они отдаляются друг от друга, и рано или поздно они перестанут соприкасаться без нашего участия. Конечно же это физически неправдоподобно, но если скорости невелики и/или используется маленький шаг симуляции, то выглядит вполне нормально. Если же рассчеты нужны, мы считаем изменения в скоростях, которые произошли при столкновении и возвращаем эти скорости вместе с идентификатором фигуры.

Apply Velocities

Имея на руках изменения скоростей, функция applyVelocities() просто суммирует их и применяет к объекту. Снова о правдоподобности речь не идет и, вполне возможно, при некоторых условиях появятся артефакты, но на моих тестовых данных я не заметил проблем с данным подходом. Да и целью эксперимента была вовсе не правдоподобность.

Результат

После этих нехитрых шагов мы будем иметь новые данные, которые мы передадим отрисовщику. Потом все сначала, и так до бесконечности. В качестве доказательства, что все это работает вот короткое видео:

Код — в этом коммите.

Заключение

ФП требует перестройки мышления. Но стоит ли оно того? Вот мои за и против.

За:

• Читаемость кода. Вместе с SRP код очень легок в понимании.
• Тестируемость. Так как результат функции не зависит от окружения мы уже имеем все необходимое для тестирования.
• На мой взгляд — самый важный пункт. Великолепная возможность распараллеливания. Каждая (да-да — каждая!) функция в нашем примере может быть вызвана несколькими потоками безопасно! Без средств синхронизации!

Против:

• Только одна ложка дегтя — даже не ложка, половник. Производительность. Вспомните, в прошлой статье в одном потоке с 2Д сеткой мы могли симулировать 8000 фигур. Сейчас всего 330. Триста тридцать, Карл!

Я десять лет проработал в геймдеве, стараясь выжимать максимум из каждой строчки. Для 3Д движка функциональный подход в том виде, в котором был представлен сегодня, несомненно, самоубийство. Однако, c++ — это не только геймдев. Не могу сказать точно, но интуиция подсказывает, что для большинства приложений ФП окажется вполне конкурентоспособной техникой.

Имея на руках несколько техник, почему бы не попробовать совместить их? В моей следующей статье я попробую скрестить ООП, DOD и ФП. Я не знаю результат, но уже вижу места, где можно значительно увеличить производительность. Поэтому оставайтесь на связи — должно быть интересно.

Автор: nikitablack

Источник