В последнее время все чаще можно встретить обсуждение интересной, но не очень популярной парадигмы — так называемой Data Oriented Design (DOD). Если вы устраиваетесь на работу, связанную с высокопроизводительными вычислениями, будьте готовы к соответствующим вопросам. Но я был очень очень удивлен, узнав, что некоторые мои коллеги не слышали об этом подходе и после недолго обсуждения отнеслись к нему скептически. В этой статье я постараюсь сравнить традиционный OOP подход с DOD.
Что такое DOD?
Данная статья была задумана как попытка сравнить разные подходы без попытки объяснить их суть. На Хабре есть несколько статей по теме, например эта. Стоит также посмотреть видео с конференции CppCon. Но в двух словах, DOD — это способ оперировать данными в cache friendly манере. Звучит непонятно, пример объяснит лучше.
#include <chrono>
#include <iostream>
#include <vector>
using namespace std;
using namespace std::chrono;
struct S
{
uint64_t u;
double d;
int i;
float f;
};
struct Data
{
vector<uint64_t> vu;
vector<double> vd;
vector<int> vi;
vector<float> vf;
};
int test1(S const & s1, S const & s2)
{
return s1.i + s2.i;
}
int test2(Data const & data, size_t const ind1, size_t const ind2)
{
return data.vi[ind1] + data.vi[ind2];
}
int main()
{
size_t const N{ 30000 };
size_t const R{ 10 };
vector<S> v(N);
Data data;
data.vu.resize(N);
data.vd.resize(N);
data.vi.resize(N);
data.vf.resize(N);
int result{ 0 };
cout << "test #1" << endl;
for (uint32_t i{ 0 }; i < R; ++i)
{
auto const start{ high_resolution_clock::now() };
for (size_t a{ 0 }; a < v.size() - 1; ++a)
{
for (size_t b{ a + 1 }; b < v.size(); ++b)
{
result += test1(v[a], v[b]);
}
}
cout << duration<float>{ high_resolution_clock::now() - start }.count() << endl;
}
cout << "test #2" << endl;
for (uint32_t i{ 0 }; i < R; ++i)
{
auto const start{ high_resolution_clock::now() };
for (size_t a{ 0 }; a < v.size() - 1; ++a)
{
for (size_t b{ a + 1 }; b < v.size(); ++b)
{
result += test2(data, a, b);
}
}
cout << duration<float>{ high_resolution_clock::now() - start }.count() << endl;
}
return result;
}
Второй тест выполняется быстрее на 30% (в VS2017 и gcc7.0.1). Но почему?
Размер структуры S равен 24 байтам. Мой процессор (Intel Core i7) имеет 32KB кэш на ядро с 64B кэш-линией (cache line). Это значит, что при запросе данных из памяти в одну кэш-линию полностью поместятся только две структуры S. В первом тесте я читаю только одно int поле, т.е. при одном обращении к памяти в одной кэш-линии будет только 2 (иногда 3) нужных нам поля. Во втором тесте я читаю такое же int значение, но из вектора. std::vector гарантирует последовательность данных. Это означает, что при обращении к памяти в одной кэш-линии будет 16 (64KB / sizeof(int) = 16) нужных нам значений. Получается, что во втором тесте мы обращаемся к памяти реже. A обращение к памяти, как известно, является слабым звеном в современных процессорах.
Как дела обстоят на практике?
Пример выше наглядно показывает преимущества использования SoA (Struct of Arrays) вместо AoS (Array of Structs), но этот пример из разряда Hello World, т.е. далек от реальной жизни. В реальном коде много зависимостей и специфических данных, которые, возможно не дадут прироста производительности. К тому же, если в тестах мы будем обращаться ко всем полям структуры, разницы в производительности не будет.
Чтобы понять реальность применения подхода я решил написать более-менее комплексный код, используя обе техники и сравнить результаты. Пускай это будет 2d симуляция твердых тел — мы создадим N выпуклых многоугольников, зададим параметры — массу, скорость и т.п. и посмотрим, сколько объектов мы сможем симулировать оставаясь на отметке 30 fps.
1. Array of Structures
1.1. Первая версия программы
Исходный код для первой версии программы можно взять из этого коммита. Сейчас мы кратко пробежимся по коду.
Для простоты программа написана для Windows и использует DirectX11 для отрисовки. Цель этой статьи — сравнение производительности на процессоре, поэтому графику мы обсуждать не будем. Класс Shape, который представляет физическое тело, выглядит так:
class Shape
{
public:
Shape(uint32_t const numVertices, float radius, math::Vec2 const pos, math::Vec2 const vel, float m, math::Color const col);
static Shape createWall(float const w, float const h, math::Vec2 const pos);
public:
math::Vec2 position{ 0.0f, 0.0f };
math::Vec2 velocity{ 0.0f, 0.0f };
math::Vec2 overlapResolveAccumulator{ 0.0f, 0.0f };
float massInverse;
math::Color color;
std::vector<math::Vec2> vertices;
math::Bounds bounds;
};
- Назначение
positionиvelocity, думаю, очевидно.vertices— вершины фигуры заданные рандомно. bounds— это ограничивающий прямоугольник, который полностью содержит фигуру — используется для предварительной проверки пересечений.massInverse— единица, разделенная на массу — мы будем использовать только это значение, поэтому будем хранить его, вместо массы.color— цвет — используется только при рендеринге, но хранится в экземпляре фигуры, задается рандомно.overlapResolveAccumulatorсм. пояснение ниже.
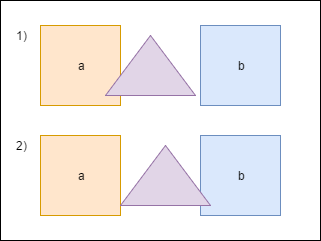
Когда треугольник пересекается с фигурой a, мы должны подвинуть его немного, чтобы исключить наложение фигур друг на друга. Также мы должны пересчитать bounds. Но после перемещения треугольник пересекает другую фигуру — b, и мы снова должны переместить его и снова пересчитать bounds. Заметьте, что после второго перемещения треугольник снова окажется над фигурой a. Чтобы избежать повторных вычислений мы будем хранить величину, на которую нужно переместить треугольник в специальном аккумуляторе — overlapResolveAccumulator — и позже будем перемещать фигуру на это значение, но только один раз.
Сердце нашей программы — это метод ShapesApp::update(). Вот его упрощенный вариант:
void ShapesApp::update(float const dt)
{
float const dtStep{ dt / NUM_PHYSICS_STEPS };
for (uint32_t s{ 0 }; s < NUM_PHYSICS_STEPS; ++s)
{
updatePositions(dtStep);
for (size_t i{ 0 }; i < _shapes.size() - 1; ++i)
{
for (size_t j{ i + 1 }; j < _shapes.size(); ++j)
{
CollisionSolver::solveCollision(_shapes[i].get(), _shapes[j].get());
}
}
}
}
Каждый кадр мы вызываем ShapesApp::updatePositions() метод, который меняет положение каждой фигуры и рассчитывает новый Shape::bounds. Затем мы проверяем каждую фигуру с каждой другой на пересечение — CollisionSolver::solveCollision(). Я использовал Separating Axis Theorem (SAT). Все эти проверки мы делаем NUM_PHYSICS_STEPS раз. Эта переменная служит нескольким целям — во-первых, физика получается более стабильная, во-вторых, она ограничивает количество объектов на экране. с++ быстр, очень быстр, и без этой переменной у нас будут десятки тысяч фигур, что замедлит отрисовку. Я использовал NUM_PHYSICS_STEPS = 20
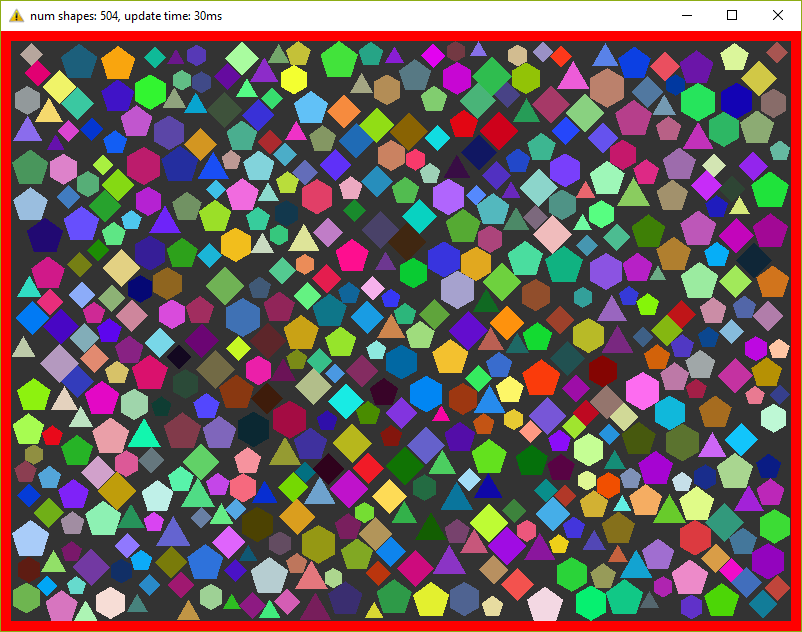
На моем стареньком ноутбуке эта программа рассчитывает 500 фигур максимум, перед тем, как fps начинает падать ниже 30. Фуууу, всего 500???! Согласен, немного, но не забывайте, что каждый кадр мы повторяем расчеты 20 раз.
Думаю, что стоит разбавить статью скриншотами, поэтому вот:
1.2. Оптимизация номер 1. Spatial Grid
Я упоминал, что хочу провести тесты на как можно более приближенной к реальности программе. То, что мы написали выше в реальности не используется — проверять каждую фигуру с каждой ооочень медленно. Для ускорения расчетов обычно используется специальная структура. Предлагаю использовать обыкновенную 2d сетку — я назвал ее Grid — которая состоит из NxM ячеек — Cell. В начале расчетов мы будем записывать в каждую ячейку объекты, которые находятся в ней. Тогда нам нужно будет всего лишь пробежаться по всем ячейкам и проверить пересечения нескольких пар объектов. Я неоднократно использовал этот подход в релизах и он зарекомендовал себя — пишется очень быстро, легко отлаживается, прост в понимании.
Коммит второй версии программы можно посмотреть здесь. Появился новый класс Grid и немного изменился метод ShapesApp::update() — теперь он вызывает методы сетки для проверки пересечений.
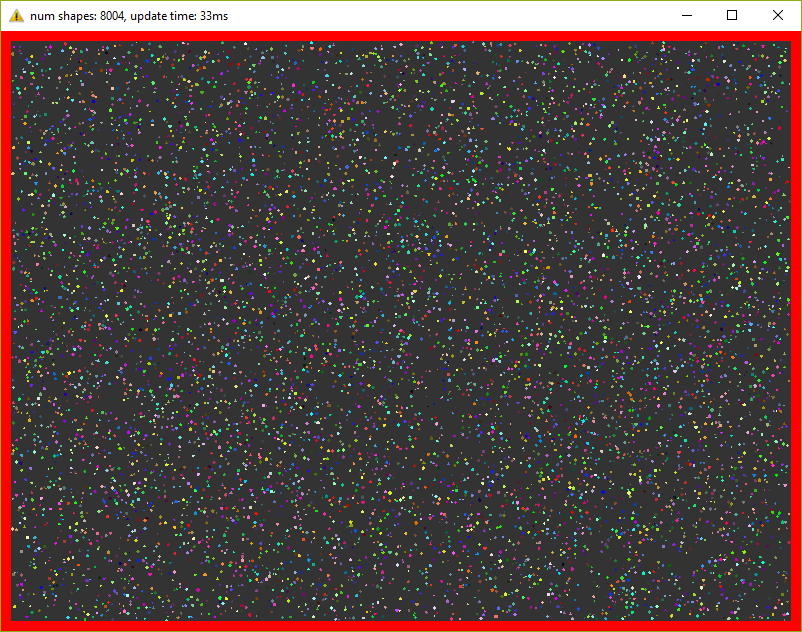
Эта версия держит уже 8000 фигур при 30 fps (не забываем про 20 итераций в каждом кадре)! Пришлось уменьшить фигуры в 10 раз, чтобы они поместились в окне.
1.3. Оптимизация номер 2. Multithreading.
Сегодня, когда даже на телефонах устанавливаются процессоры с четырьмя ядрами, игнорировать многопоточность просто глупо. В этой, последней, оптимизации мы добавим пул потоков и разделим основные задачи на равные таски. Так, например, метод ShapesApp::updatePositions, который раньше пробегал по всем фигурам, устанавливая новую позицию и пересчитывая bounds, теперь пробегает только по части фигур, уменьшая, тем самым, нагрузку на одно ядро. Класс пула был честно скопипастен отсюда. В тестах я использую четыре потока (считая основной). Готовую версию можно найти здесь.
Разделение основных задач добавило немного головной боли. Так например, если фигура пересекает границу ячейки в сетке, то она будет находится одновременно в нескольких ячейках:
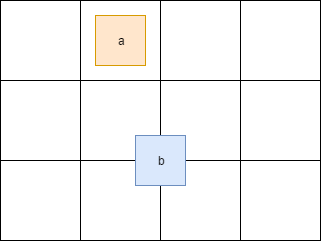
Здесь фигура a находится в одной ячейке, тогда как b сразу в четырех. Поэтому доступ к этим ячейкам необходимо синхронизировать. Также нужно синхронизировать доступ к некоторым полям класса Shape. Для этого мы добавили std::mutex в Shape и Cell.
Запустив эту версию я могу наблюдать 13000 фигур при 30 fps. Для такого количества объектов пришлось увеличить окно! И снова — в каждом кадре мы повторяем симуляцию 20 раз.

2. Structure of Arrays
2.1. Первая версия программы
То, что мы писали выше я называю традиционным подходом — я пишу такой код много лет и читаю, в основном, похожий код. Но теперь мы убьем структуру Shape и посмотрим — сможет ли эта небольшая модификация повлиять на производительность. Ко всеобщей радости рефакторинг оказался не сложным, даже тривиальным. Вместо Shape мы будем использовать структуру с векторами:
struct ShapesData
{
std::vector<math::Vec2> positions;
std::vector<math::Vec2> velocities;
std::vector<math::Vec2> overlapAccumulators;
std::vector<float> massesInverses;
std::vector<math::Color> colors;
std::vector<std::vector<math::Vec2>> vertices;
std::vector<math::Bounds> bounds;
};
И передаем мы эту структуру так:
solveCollision(struct ShapesData & data, std::size_t const indA, std::size_t const indB);Т.е. вместо конкретных фигур передаются их индексы и в методе из нужных векторов берутся нужные данные.
Эта версия программы выдает 500 фигур при 30 fps, т.е. не отличается от самой первой версии. Связано это с тем, что измерения проводятся на малом количестве данных и к тому же самый тяжелый метод использует почти все поля структуры.
Далее без картинок, т.к. они точно такие же, как были ранее.
2.2. Оптимизация номер 1. Spatial Grid
Все как и раньше, меняем только AoS на SoA. Код здесь. Результат лучше, чем был ранее — 9500 фигур (было 8000), т.е. разница в производительности около 15%.
2.3. Оптимизация номер 2. Multithreading
Снова берем старый код, меняем структуры и получаем 15000 фигур при 30 fps. Т.е. прирост производительности около 15%. Исходный код финальной версии лежит здесь.
3. Заключение
Изначально код писался для себя с целью проверить различные подходы, их производительность и удобство. Как показали результаты, небольшое изменение в коде может дать довольно ощутимый прирост. А может и не дать, может быть даже наоборот — производительность будет хуже. Так например, если нам нужна всего один экземпляр, то используя стандартный подход мы прочитаем его из памяти только один раз и будем иметь доступ ко всем полям. Используя же структуру векторов, мы вынуждены будем запрашивать каждое поле индивидуально, имея cache-miss при каждом запросе. Плюс ко всему немного ухудшается читабельность и усложняется код.
Поэтому однозначно ответить — стоит ли переходить на новую парадигму всем и каждому — невозможно. Когда я работал в геймдеве над игровым движком, 10% прироста производительности — внушительная цифра. Когда я писал пользовательские утилиты типа лаунчера, то применение DOD подхода вызвало бы только недоумение коллег. В общем, профилируйте, измеряйте и делайте выводы сами :).
Автор: nikitablack






