Параллельное программирование с помощью вычислительного графа

Есть приложения, которые хорошо реализуются как системы передачи сообщений. Сообщениями в широком смысле может быть что угодно – блоки данных, управляющие «сигналы» и т.д. Логика же состоит из узлов, обрабатывающих сообщения, и связей между ними. Такая структура естественно представляется графом, по рёбрам которого «текут» сообщения, обрабатываемые в узлах. Наиболее устоявшееся название такой модели – вычислительный граф.

С помощью вычислительного графа можно установить зависимости между задачами и в какой-то мере программно реализовать «dataflow архитектуру».

В этом посте я опишу, как реализовать такую модель на С++, используя библиотеку Intel® Threading Building Blocks (Intel® TBB), а именно класс tbb::flow::graph.

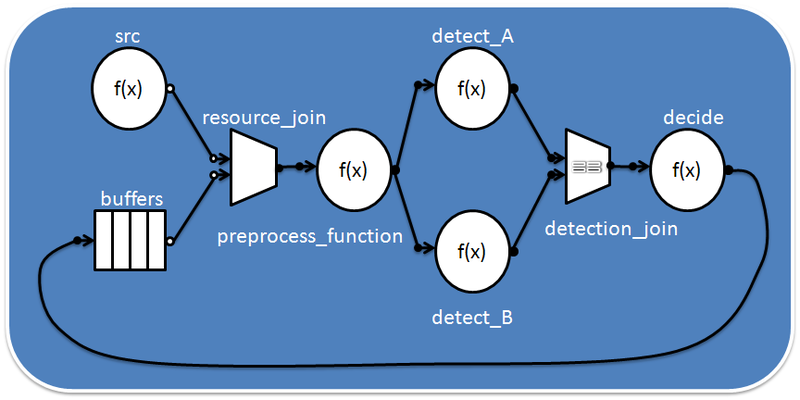
Что такое Intel TBB и класс tbb::flow::graph

Intel® Threading Building Blocks – библиотека шаблонов С++ для параллельного программирования. Распространяется она бесплатно в реализации с открытым исходным кодом, но есть и коммерческая версия. В бинарном виде выпускается для Windows*, Linux* и OS X*.

В TBB есть множество готовых алгоритмов, конструкций и структур данных, «заточенных» для использования в параллельных вычислениях. В том числе, есть и конструкции, позволяющие реализовать вычислительный граф, о котором и пойдёт речь.

Граф, как известно, состоит из вершин (узлов) и рёбер. Вычислительный граф tbb::flow::graph также состоит из узлов (node), рёбер (edge) и объекта всего графа.

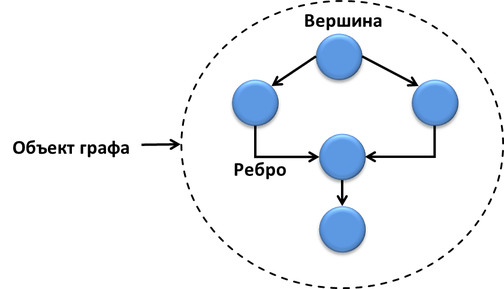
Узлы графа имеют интерфейсы отправителя и получателя, управляют сообщениями или выполняют какие-то функции. Рёбра соединяют узлы графа и являются «каналами» передачи сообщений.

Тело каждого узла представлено задачей TBB и может исполняться параллельно с другими, если между ними нет зависимостей. В TBB многие параллельные алгоритмы (или все) строятся на задачах – небольших элементах работы (инструкций), которые исполняются рабочими потоками. Между задачами могут быть зависимости, они могут динамически перераспределяться между потоками. Благодаря использованию задач можно достигнуть оптимальной гранулярности и баланса нагрузки на CPU, а также строить более высокоуровневые параллельные конструкции на их основе – такие как tbb::flow::graph.

Самый простой граф зависимостей

Граф, состоящий из двух вершин, соединённых одним ребром, одна из которых печатает “Hello”, а вторая “World”, схематично можно изобразить так:

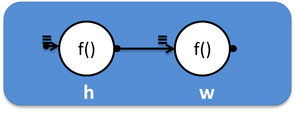
А в коде это будет выглядеть так:

#include <iostream>
#include <tbb/flow_graph.h>

int main(int argc, char *argv[]) {
	tbb::flow::graph g; 
	tbb::flow::continue_node< tbb::flow::continue_msg > 
		h( g, []( const tbb::flow::continue_msg & ) { std::cout << "Hello "; } );

	tbb::flow::continue_node< tbb::flow::continue_msg > 
		w( g, []( const tbb::flow::continue_msg & ) { std::cout << "Worldn"; } );
                            
	tbb::flow::make_edge( h, w );

	h.try_put(tbb::flow::continue_msg());
	g.wait_for_all();
	return 0;
}

Здесь создаётся объект графа g и два узла типа continue_node – h и w. Эти узлы принимают и передают сообщение типа continue_msg – внутренне управляющее сообщение. Они используются для построения графов зависимостей, когда тело узла исполняется лишь после того, как получено сообщение от предшественника.

Каждый из continue_node исполняет некоторый условно полезный код – печать “Hello” и “World”. Узлы объединяются ребром с помощью метода make_edge. Всё, структура вычислительного графа готова – можно запускать его на исполнение, подавая ему на вход сообщение методом try_put. Далее граф отрабатывает, и, чтобы убедиться, что все его задачи выполнены, ждём с помощью метода wait_for_all.

Простой граф передачи сообщений

Представьте, что наша программа должна посчитать выражение x²+x³ для x от 1 до 10. Да, это не самая сложная вычислительная задача, но вполне сгодиться для демонстрации.

Попробуем представить подсчёт выражения в виде графа. Первый узел будет принимать значения x из входящего потока данных и отсылать его узлам, возводящим в куб и в квадрат. Операции возведения в степень не зависят друг от друга и могут исполняться параллельно. Для сглаживания возможных дисбалансов они передают свой результат в буферные узлы. Далее идёт объединяющий узел, поставляющий результаты возведения в степень суммирующему узлу, на чём вычисление и заканчивается:

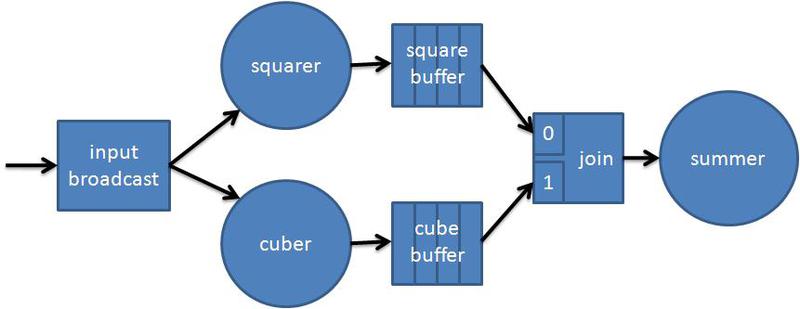
Код такого графа:

#include <tbb/flow_graph.h>
#include <windows.h>

using namespace tbb::flow;

struct square { 
  int operator()(int v) {
    printf("squaring %dn", v);
    Sleep(1000);		 
    return v*v; 
  }
};

struct cube {
  int operator()(int v) {
     printf("cubing %dn", v);
    Sleep(1000); 
    return v*v*v; 
  }
};

class sum {
  int &my_sum;
public:
  sum( int &s ) : my_sum(s) {}
  int operator()( std::tuple<int,int> v ) {
    printf("adding %d and %d to %dn", std::get<0>(v), std::get<1>(v), my_sum);
    my_sum += std::get<0>(v) + std::get<1>(v);
    return my_sum;
  }
};

int main(int argc, char *argv[]) {
	int result = 0;

	graph g; 
	broadcast_node<int> input (g);
	function_node<int,int> squarer( g, unlimited, square() );
	function_node<int,int> cuber( g, unlimited, cube() );
	buffer_node<int> square_buffer(g);
	buffer_node<int> cube_buffer(g);
	join_node< std::tuple<int,int>, queueing > join(g);
	function_node<std::tuple<int,int>,int>
		summer( g, serial, sum(result) );
 
	make_edge( input, squarer );
	make_edge( input, cuber );
	make_edge( squarer, square_buffer );
	make_edge( squarer, input_port<0>(join) );
	make_edge( cuber, cube_buffer );
	make_edge( cuber, input_port<1>(join)		);
	make_edge( join, summer );
 
	for (int i = 1; i <= 10; ++i)
		input.try_put(i);
	g.wait_for_all();
 
	printf("Final result is %dn", result);
	return 0;
}

Функция Sleep(1000) добавлена для визуализации процесса (пример компилировался на Windows, используйте эквивалентные вызовы на других платформах). Далее всё как в первом примере – создаём узлы, объединяем их рёбрами и запускаем на исполнение. Второй параметр в function_node (unlimited или serial) определяет, сколько экземпляров тела узла может исполняться параллельно. Узел типа join_node определяет готовность входных данных/сообщений на каждой входе, и когда оба готовы – передаёт их следующему узлу в виде std::tuple.

Решение проблемы «обедающих философов» с помощью tbb::flow::graph

Из википедии:
«Проблема обедающих философов» — классический пример, используемый в информатике для иллюстрации проблем синхронизации в дизайне параллельных алгоритмов и техник решения этих проблем.

В задаче несколько философов сидят за столом, и могут либо есть, либо думать, но не одновременно. В нашем варианте философы едят лапшу палочками – чтобы есть нужно две палочки, но в наличии на каждого по одной:

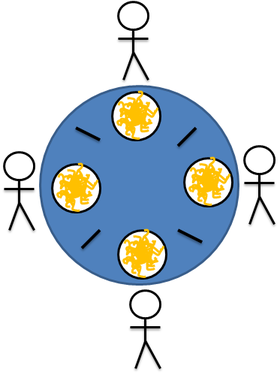
В такой ситуации может случиться deadlock (взаимная блокировка), если, например, каждый философ захватит левую от себя палочку, поэтому требуется синхронизация действий между обедающими.

Попробуем представить стол с философами в виде tbb::flow::graph. Каждый философ будет представлен двумя узлами: join_node для захвата палочек и function_node для осуществления задач «есть» и «думать». Место для палочки на столе реализуем через queue_node. В очереди queue_node может быть не больше одной палочки, и если она там есть – она доступна для захвата. Граф будет выглядеть так:

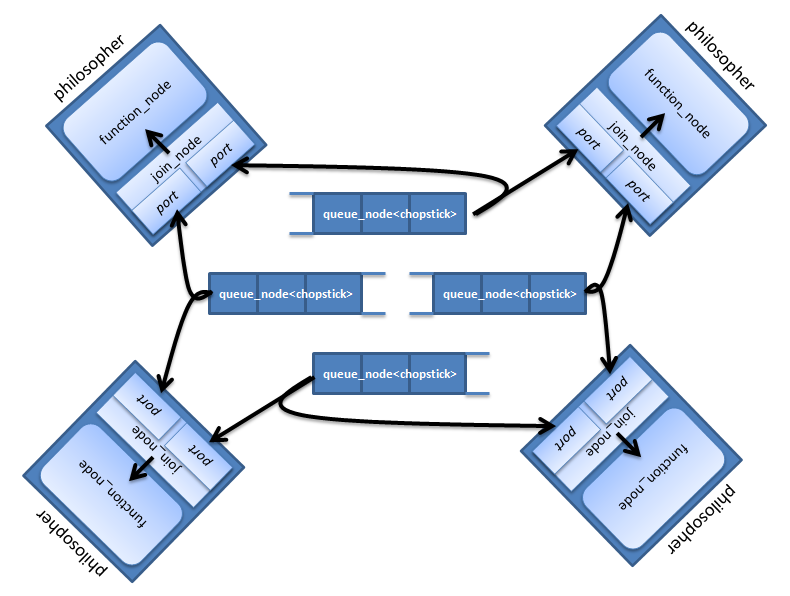
Функция main с некоторыми константами и заголовочными файлами:

#include <windows.h>
#include <tbb/flow_graph.h>
#include <tbb/task_scheduler_init.h>

using namespace tbb::flow;

const char *names[] = 
{ "Archimedes", "Aristotle", "Democritus", "Epicurus", "Euclid", 
"Heraclitus", "Plato", "Pythagoras", "Socrates", "Thales" };

….
int main(int argc, char *argv[]) {
  int num_threads = 0;
  int num_philosophers = 10;
  if ( argc > 1 ) num_threads = atoi(argv[1]);
  if ( argc > 2 ) num_philosophers = atoi(argv[2]);

  if ( num_threads < 1 || num_philosophers < 1 || num_philosophers > 10 ) exit(1);

  tbb::task_scheduler_init init(num_threads);
  graph g;
  printf("n%d philosophers with %d threadsnn", 
         num_philosophers, num_threads);

  std::vector< queue_node<chopstick> * > places;
  for ( int i = 0; i < num_philosophers; ++i ) {
    queue_node<chopstick> *qn_ptr = new queue_node<chopstick>(g);
    qn_ptr->try_put(chopstick());
    places.push_back( qn_ptr );
  }

  std::vector< philosopher > philosophers;
  for ( int i = 0; i < num_philosophers; ++i ) {
    philosophers.push_back( philosopher( names[i], g,
                                         places[i], 
                                         places[(i+1)%num_philosophers] ) );
    g.run( philosophers[i] );
  }
  g.wait_for_all();

  for ( int i = 0; i < num_philosophers; ++i ) philosophers[i].check();

  return 0;
}

После обработки параметров командной строки библиотека инициализируется созданием объекта типа tbb::task_scheduler_init. Это позволяет управлять моментом инициализации и вручную задавать количество потоков-обработчиков. Без этого инициализация пройдёт автоматически. Далее создаётся объект графа g. «Места для палочек» queue_node помещаются в std::vector, и в каждую очередь помещается по палочке.

Дальше похожим способом создаются и философы – помещаются в std::vector. Объект каждого философа передаётся функции run объекта графа. Класс philosopher будет содержать operator(), и функция run позволяет исполнить этот функтор в задаче, дочерней к корневой задаче объекта графа g. Так мы сможем дождаться исполнения этих задач во время вызова g.wait_for_all().

Класс philosopher:

const int think_time = 1000; 
const int eat_time = 1000; 
const int num_times = 10; 

class chopstick {}; 

class philosopher { 
public: 

  typedef queue_node< chopstick > chopstick_buffer; 
  typedef join_node< std::tuple<chopstick,chopstick> > join_type; 

  philosopher( const char *name, graph &the_graph,
               chopstick_buffer *left, chopstick_buffer *right ) : 
  my_name(name), my_graph(&the_graph),
  my_left_chopstick(left), my_right_chopstick(right),
  my_join(new join_type(the_graph)), my_function_node(NULL),
  my_count(new int(num_times)) {} 

  void operator()(); 
  void check(); 

private: 

  const char *my_name; 
  graph *my_graph; 
  chopstick_buffer *my_left_chopstick; 
  chopstick_buffer *my_right_chopstick; 
  join_type *my_join; 
  function_node< join_type::output_type, continue_msg > *my_function_node; 
  int *my_count; 

  friend class node_body; 

  void eat_and_think( ); 
  void eat( ); 
  void think( ); 
  void make_my_node(); 

};

У каждого философа есть имя, указатели на объект графа и на левую и правую палочки, узел join_node, функциональный узел function_node и счётчик my_count, отсчитывающий, сколько раз философ думал и ел.

operator()(), вызываемый функцией run графа, реализован так, чтобы философ сначала думал, а потом присоединял себя к графу.

void philosopher::operator()() { 
  think(); 
  make_my_node(); 
} 

Методы think и eat просто спят положенное время:
void philosopher::think() { 
  printf("%s thinkingn", my_name ); 
  Sleep(think_time); 
  printf("%s done thinkingn", my_name ); 
} 

void philosopher::eat() { 
  printf("%s eatingn", my_name ); 
  Sleep(eat_time); 
  printf("%s done eatingn", my_name ); 
}

Метод make_my_node создаёт функциональный узел, и связывает и его, и join_node с остальным графом:

void philosopher::make_my_node() { 
  my_left_chopstick->register_successor( input_port<0>(*my_join) ); 
  my_right_chopstick->register_successor( input_port<1>(*my_join) ); 
  my_function_node = 
    new function_node< join_type::output_type, continue_msg >( *my_graph, 
      serial, node_body( *this ) ); 
  make_edge( *my_join, *my_function_node ); 
}

Обратите внимание, что граф создаётся динамически – ребро формируется методом register_successor. Не обязательно сначала полностью создавать структуру графа, а потом запускать его на исполнение. В TBB есть возможность менять эту структуру на лету, даже когда граф уже запущен – удалять и добавлять новые узлы. Это добавляет ещё больше гибкости концепции вычислительного графа.

Класс node_body — простой функтор, вызывающий метод philosopher::eat_and_think():

class node_body { 
  philosopher &my_philosopher; 
public: 
  node_body( philosopher &p ) : my_philosopher(p) { } 
  void operator()( philosopher::join_type::output_type ) { 
    my_philosopher.eat_and_think(); 
  } 
};

Метод eat_and_think вызывает функцию eat() и декрементирует счётчик. Дальше философ кладёт свои палочки на стол и думает. А если он поел и подумал положенное число раз, он встаёт из-за стола – разрывает связи своего join_node с графом методом remove_successor. Здесь опять видна динамическая структура графа – часть узлов удаляется, пока остальные продолжают работать.

void philosopher::eat_and_think( ) { 
  eat(); 
  --(*my_count); 

  if (*my_count > 0) { 
    my_left_chopstick->try_put( chopstick() ); 
    my_right_chopstick->try_put( chopstick() ); 
    think(); 
  } else { 
    my_left_chopstick->remove_successor( input_port<0>(*my_join) );
    my_right_chopstick->remove_successor( input_port<1>(*my_join) );
    my_left_chopstick->try_put( chopstick() ); 
    my_right_chopstick->try_put( chopstick() ); 
  } 
}

В нашем графе есть ребро от queue_node (места для палочки) к философу, точнее его join_node. А в обратную сторону нет. Тем не менее, метод eat_and_think может вызывать try_put для того, чтобы положить палочку обратно в очередь.

В конце функции main() для каждого философа вызывается метод check, который удостоверяется, что философ поел и подумал правильное количество раз и делает необходимую «очистку»:

void philosopher::check() { 
  if ( *my_count != 0 ) { 
    printf("ERROR: philosopher %s still had to run %d more timesn", my_name, *my_count); 
    exit(1); 
  } else { 
    printf("%s done.n", my_name); 
  } 
  delete my_function_node; 
  delete my_join; 
  delete my_count; 
}

Deadlock в этом примере не случается благодаря использованию join_node. Этот тип узлов создаёт std::tuple из полученных с обоих входов объектов. При этом входные данные не потребляются сразу при поступлении. join_node сначала дожидается, когда данные появятся на обоих входах, потом пытается их зарезервировать по очереди. Если эта операция успешна – только тогда они «потребляются» и из них создаётся std::tuple. Если резервирование хотя бы одного входного «канала» не получилось – те, что уже зарезервированы, отпускаются. Т.е. если философ может захватить одну палочку, но вторая занята – он отпустить первую и подождёт, не блокируя соседей понапрасну.

Этот пример с обедающими философами демонстрирует несколько возможностей TBB графа:

• Использование join_node для обеспечения синхронизации доступа к ресурсам
• Динамическое построение графа – узлы могут добавляться и удаляться во время работы
• Отсутствие единых точек входа и выхода, граф может иметь петли
• Использование функции run графа

Типы узлов

tbb::flow::graph предоставляет довольно широкий набор вариантов узлов. Их можно разделить на четыре группы: функциональные (functional), буферизующие, объединяющие и разделяющие, и прочие. Список типов узлов с условными обозначениями:

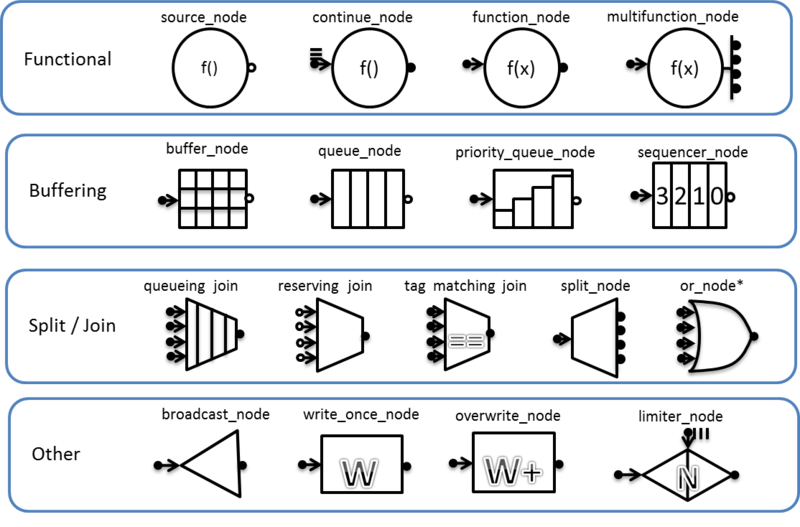
Заключение

С помощью графа, реализованного в Intel TBB, можно создать сложную и интересную логику параллельной программы, иногда называемую «неструктурированным параллелизмом». Вычислительный граф позволяет организовать зависимости между задачами, строить приложения, основанные на передаче сообщений и событий.

Структура графа может быть как статической, так и динамической – узлы и рёбра могут добавляться и удаляться «на лету». Можно соединять отдельные подграфы в большой граф.

Большая часть материала базируется на англоязычных публикациях моих заокеанских коллег.

Для тех, кто заинтересовался, пробуйте:

Скачать библиотеку Intel® Threading Building Blocks (Версия с открытым исходным кодом):
http://threadingbuildingblocks.org

Коммерческая версия Intel TBB (функционально не отличается):
http://software.intel.com/en-us/intel-tbb

Англоязычные блоги о tbb::flow::graph:
http://software.intel.com/en-us/tags/17218
http://software.intel.com/en-us/tags/17455

Автор: krogozh

Источник