Нейронная сеть Хопфилда на пальцах

Статья посвящена введению в нейронные сети и примеру их реализации. В первой части дано небольшое теоретическое введение в нейронные сети на примере нейронной сети Хопфилда. Показано, как осуществляется обучение сети и как описывается ее динамика. Во второй части показано, как можно реализовать алгоритмы, описанные в первой части при помощи языка С++. Разработанная программа наглядно показывает способность нейронной сети очищать от шума ключевой образ. В конце статьи есть ссылка на исходный код проекта.

Теоретическое описание

Введение

Для начала, необходимо определить, что такое нейрон. В биологии нейрон — специализированная клетка, из которой состоит нервная система. Биологический нейрон имеет строение, показанное на рис.1.

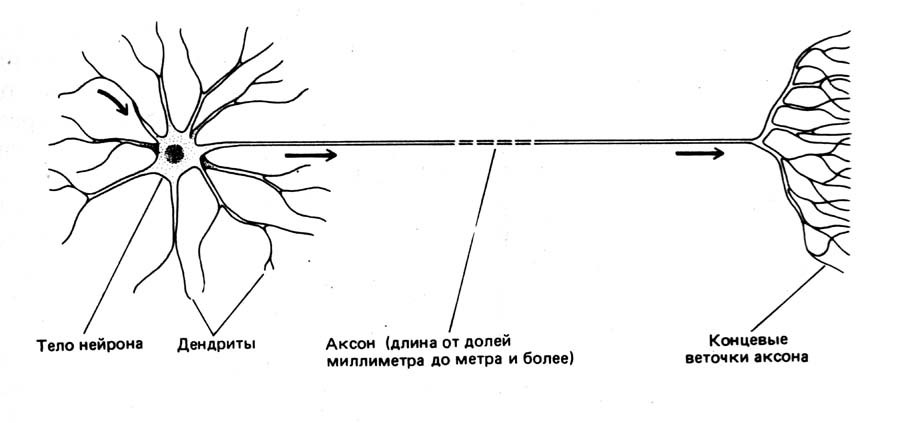
Рис.1 Схема нейрона

Нейронную сеть можно ввести как совокупность нейронов и их взаимосвязей. Следовательно, для того, чтобы определить искусственную (не биологическую) нейронную сеть необходимо:

1. Задать архитектуру сети;
2. Определить динамику отдельных элементов сети — нейронов;
3. Определить правила, по которым нейроны будут взаимодействовать между собой;
4. Описать алгоритм обучения, т.е. формирования связей для решения поставленной задачи.

В качестве архитектуры нейронной сети будет использоваться сеть Хопфилда. Данная модель, видимо, является наиболее распространенной математической моделью в нейронауке. Это обусловлено ее простотой и наглядность. Сеть Хопфилда показывает, каким образом может быть организована память в сети из элементов, которые не являются очень надежными. Экспериментальные данные показывают, что при увеличении количества вышедших из строя нейронов до 50%, вероятность правильного ответа крайне близка к 100%. Даже поверхностное сопоставление нейронной сети (например, мозга) и Фон-Неймановской ЭВМ показывает, насколько сильно различаются эти объекты: к примеру, частота изменения состояний нейронов («тактовая частота») не превышает 200Гц, тогда как частота изменения состояния элементов современного процессора может достигать нескольких ГГц (Гц).
Формальное описание сети Хопфилда

Сеть состоит из N искусственных нейронов, аксон каждого нейрона связан с дендритами остальных нейронов, образуя обратную связь. Архитектура сети изображена на рис. 2.

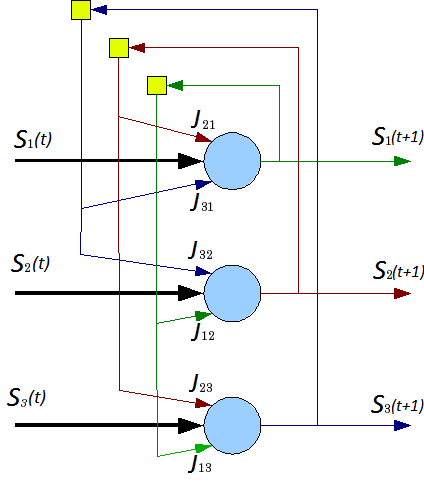
Рис.2 Архитектура нейронной сети Хопфилда

Каждый нейрон может находиться в одном из 2-х состояний:

где — состояние нейрона в момент . «Возбуждению» нейрона соответствует , а «торможению» . Дискретность состояний нейрона отражает нелинейный, пороговый характер его функционирования и известный в нейрофизиологи как принцип «все или ничего».

Динамика состояния во времени -ого нейрона в сети из нейронов описывается дискретной динамической системой:

где — матрица весовых коэффициентов, описывающих взаимодействие дендритов -ого нейрона с аксонами -ого нейрона.

Стоит отметить, что и случай не рассматриваются.

Обучение и устойчивость к шуму

Обучение сети Хопфилда выходным образам сводится к вычислению значений элементов матрицы . Формально можно описать процесс обучения следующим образом: пусть необходимо обучить нейронную сеть распознавать образов, обозначенных . Входной образ представляет собой: где — шум, наложенный на исходный образ .
Фактически, обучение нейронной сети — определение нормы в пространстве образов . Тогда, очистка входного образа от шума можно описать как минимизацию этого выражения.

Важной характеристикой нейронной сети является отношение числа ключевых образов , которые могут быть запомнены, к числу нейронов сети : . Для сети Хопфилда значение не больше 0.14.

Вычисление квадратной матрицы размера для ключевых образов производится по правилу Хебба:

где означает -ый элемент образа .

Стоит отметить, что в силу коммутативности операции умножения, соблюдается равенство

Входной образ, который предъявляется для распознавания соответствует начальным данным для системы, служащий начальным условием для динамической системы (2):

Уравнений (1), (2), (3), (4) достаточно для определения искусственной нейронной сети Хопфилда и можно перейти к ее реализации.

Реализация нейронной сети Хопфилда

Реализация нейронной сети Хопфилда, определенной выше будет производиться на языке C++. Для упрощения экспериментов, добавим основные определения типов, напрямую связанных с видом нейрона и его передаточной функции в класс simple_neuron, а производные определим далее.

Самыми основными типами, напрямую связанными с нейроном являются:

1. тип весовых коэффициентов (выбран float);
2. тип, описывающий состояния нейрона (введен перечислимый тип с 2 допустимыми значениями).

На основе этих типов можно ввести остальные базовые типы:

1. тип, описывающий состояние сети в момент (выбран стандартный контейнер vector);
2. тип, описывающий матрицу весовых коэффициентов связей нейронов (выбран контейнер vector контейнеров vector).

struct simple_neuron {
    enum state {LOWER_STATE=-1, UPPER_STATE=1};

    typedef float coeff_t;    <<(1)
    typedef state state_t;    <<(2)
...
};

typedef simple_neuron neuron_t;
typedef neuron_t::state_t state_t;

typedef vector<state_t> neurons_line;                     <<(3)
typedef vector<vector<neuron_t::coeff_t>> link_coeffs;    <<(4)

Обучение сети, или, вычисление элементов матрицы в соответствии с (3) производится функцией learn_neuro_net, принимающей на вход список обучающих образов и возвращающей объект типа link_coeffs_t. Значения вычисляются только для нижнетреугольных элементов. Значения верхнетреугольных элементов вычисляются в соответствии с (4). Общий вид метода learn_neuro_net показан в листинге 2.

link_coeffs learn_neuro_net(const list<neurons_line> &src_images) {
    link_coeffs result_coeffs;
    size_t neurons_count = src_images.front().size();

    result_coeffs.resize(neurons_count);
    for (size_t i = 0; i < neurons_count; ++i) {
        result_coeffs[i].resize(neurons_count, 0);
    }

    for (size_t i = 0; i < neurons_count; ++i) {
        for (size_t j = 0; j < i; ++j) {
            neuron_t::coeff_t val = 0;
            val = std::accumulate(
                begin(src_images),
                end(src_images),
                neuron_t::coeff_t(0.0),
                [i, j] (neuron_t::coeff_t old_val, const neurons_line &image) -> neuron_t::coeff_t{
                    return old_val + (image[i] * image[j]);
                });
            result_coeffs[i][j] = val;
            result_coeffs[j][i] = val;
        }
    }

    return result_coeffs;
}

Обновление состояний нейронов реализовано с помощью функтора neuro_net_system. Аргументом метода _do функтора является начальное состояние , являющееся распознаваемых образом (в соответствии с (5)) — ссылка на объект типа neurons_line.

Метод функтора модифицирует передаваемый объект типа neurons_line до состояния нейронной сети в момент времени . Значение жестко не фиксировано и определяется выражением:

т.е., когда состояние каждого нейрона не изменилось за 1 «такт».

Для вычисления (2) применены 2 алгоритма STL:

1. std::inner_product для вычисления суммы произведений весовых коэффициентов и состояний нейронов (т.е. вычисление (2) для определенного );
2. std::transform для вычисления новых значений для каждого нейрона (т.е. вычисление пункта выше для каждого возможного )

Исходный код функтора neurons_net_system и метода calculate класса simple_neuron показан в листинге 3.

struct simple_neuron {
...
    template <typename _Iv, typename _Ic>
    static state_t calculate(_Iv val_b, _Iv val_e, _Ic coeff_b) {
        auto value = std::inner_product(
                    val_b,
                    val_e,
                    coeff_b,
                    coeff_t(0)
                    );

        return value > 0 ? UPPER_STATE : LOWER_STATE;
    }
};

struct neuro_net_system {
    const link_coeffs &_coeffs;
    neuro_net_system(const link_coeffs &coeffs): _coeffs(coeffs) {}
    bool do_step(neurons_line& line) {
        bool value_changed = false;

        neurons_line old_values(begin(line), end(line));
        link_coeffs::const_iterator it_coeffs = begin(_coeffs);

        std::transform(
            begin(line),
            end(line), 
            begin(line), 
            [&old_values, &it_coeffs, &value_changed] (state_t old_value) -> state_t {
                auto new_value = neuron_t::calculate(
                    begin(old_values),
                    end(old_values),
                    begin(*it_coeffs++)
                    );

                value_changed = (new_value != old_value) || value_changed;

                return new_value;
            });

        return value_changed;
    }
    size_t _do(neurons_line& line) {
        bool need_continue = true;
        size_t steps_done = 0;

        while (need_continue) {
            need_continue = do_step(line);
            ++steps_done;
        }

        return steps_done;
    }
};

Для вывода в консоль входных и выходных образов создан тип neurons_line_print_descriptor, который хранит ссылку на образ и формат форматирования (ширину и высоту прямоугольника, в который будет вписан образ). Для этого типа переопределен оператор <<. Исходный код типа neurons_line_print_descriptor и оператора вывода в поток показан в листинге 4.

struct neurons_line_print_descriptor {
    const neurons_line &_line;
    const size_t _width;
    const size_t _height;

    neurons_line_print_descriptor (
        const neurons_line &line,
        size_t width,
        size_t height
        ): _line(line), 
           _width(width),
           _height(height)
        {}
};

template <typename Ch, typename Tr>
std::basic_ostream<Ch, Tr>& 
operator << (std::basic_ostream<Ch, Tr>&stm, const neurons_line_print_descriptor &line) {
    neurons_line::const_iterator it = begin(line._line), it_end = end(line._line);

    for (size_t i = 0; i < line._height; ++i) {
        for (size_t j = 0; j < line._width; ++j) {
            stm << neuron_t::write(*it);
            ++it;
        }
        stm << endl;
    }

    return stm;
}

Пример работы нейронной сети

Для проверки работоспособности реализации, нейронная сеть была обучена 2 ключевым образам:

Рис.3 Ключевые образы

На вход подавались искаженные образы. Нейронная сеть корректно распознала исходные образы. Искаженные образы и распознанные образы показаны на рис.4, 5

Рис.4 Распознавание образа 1

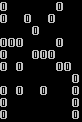
Рис.5 Распознавание образа 2

Запуск программы производится из командной строки строчкой вида: AppName WIDTH HEIGHT SOURCE_FILE [LEARNE_FILE_N], где:

AppNaame - название исполняемого файла;
WIDTH, HEIGHT - ширина и высота прямоугольника, в который будут вписываться выходной и ключевые образы;
SOURCE_FILE - исходный файл с начальным образом;
[LEARNE_FILE_N] - один или несколько файлов с ключывыми образами (через пробел).

Исходный код выложен на GitHub -> https://github.com/RainM/hopfield_neuro_net

В репозитории проект CMake, из которого можно сгенерировать проект Visual Studio (VS2015 компилирует проект успешно) или обычные Unix Makefile’ы.

Использованная литература

1. Г.Г. Малинецкий. Математические основы синергетики. Москва, URSS, 2009.
2. Статья «Нейронная_сеть_Хопфилда» на Википедии.

Автор: RainM

Источник