В школе, когда мы решали уравнения или считали формулы, мы пытались их сперва сократить несколько раз, к примеру Z = X - (Y + X) сокращается в Z = -Y. В современных компиляторах это подмножество так называемых peephole-оптимизаций, в которых мы по, грубо говоря, набору шаблонов сокращаем выражения, заменяем инструкции на более быстрые для конкретного процессора и т.п. В этой статье я собрал наборчик таких оптимизаций, которые удалось найти в исходниках LLVM, GCC и .NET Core (CoreCLR).
Начнем с простых примеров:
X * 1 => X
-X * -Y => X * Y
-(X - Y) => Y - X
X * Z - Y * Z => Z * (X - Y) проверим последний пример в С++ и в C#:
int Test(int x, int y, int z) {
return x * z - y * z; // => z * (x - y)
}и посмотрим на ассемблер от Clang (LLVM), GCC, MSVC и .NET Core:

Все три компилятора С++ (GCC, Clang и MSVC) сократили одно умножение (видим только одну инструкцию imul). C# с RyuJIT этого не сделал, но не спешите его за это ругать, просто этот класс оптимизаций там доступен в ограниченном составе. Что бы вы понимали — реализация всей InstCombine трансформации в LLVM занимает более 30к строк кода (+20к строк на DAGCombiner.cpp), к тому же эта трансформация частенько становится причиной долгой компиляции. Вот, кстати, участок ответственный за эту оптимизацию там. В GCC есть специальный DSL, на котором описываются пипхол оптимизации, вот и сниппет).
Я решил, ради статьи, попробовать реализовать эту оптимизацию в C# JIT (подержите мое пиво):
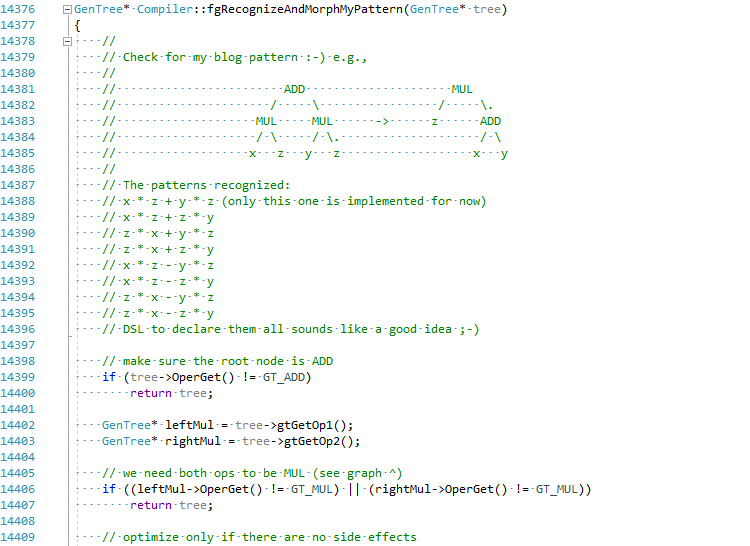
Полный коммит можно можно увидеть тут EgorBo/coreclr. Давайте теперь проверим мое улучшение ( в Visual Studio 2019 + Disasmo:
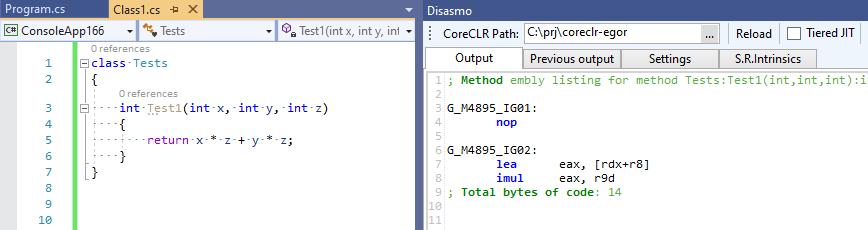
Работает! lea + imul вместо imul, imul и add.
Давайте вернемся к С++ и отследим эту оптимизацию в Clang. Для этого попросим clang выдать нам первоначальный LLVM IR через -emit-llvm -g0, а потом отдать его LLVM оптимизатору, используя параметры -O2 -print-before-all -print-after-all для того, чтобы уловить момент, какая именно трансформация из набора -O2 уберет умножение (всё это можно увидеть на замечательно ресурсе godbolt.org):
; *** IR Dump Before Combine redundant instructions ***
define dso_local i32 @_Z5Case1iii(i32, i32, i32) {
%4 = mul nsw i32 %0, %2
%5 = mul nsw i32 %1, %2
%6 = sub nsw i32 %4, %5
ret i32 %6
}
; *** IR Dump After Combine redundant instructions ***
define dso_local i32 @_Z5Case1iii(i32, i32, i32) {
%4 = sub i32 %0, %1
%5 = mul i32 %4, %2
ret i32 %5
}Там же на godbolt можно так же развлекаться с инструментами LLVM — opt (оптимизатор) и llc (для компиляции LLVM IR в asm):

Вернемся к примерам. Этот очень милый пример я нашёл в GCC.
X == C - X => false if C is oddИ ведь правда: если С (константа, литерал) четное то, можно, например, записать 4 == 8 - 4. Но если вместо 8 записать любое нечетное то вы не сможете найти такое X чтобы равенство выполнилось:
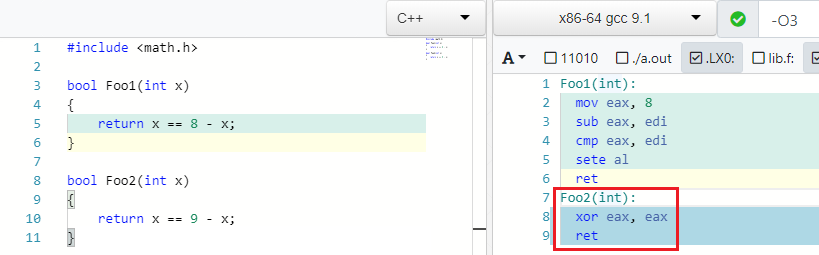
IEEE754 наносит ответный удар
Многие оптимизации работают для разных типов данных, например byte, int, unsigned, float, double. С последними не так всё просто и оптимизации связаны по рукам и ногам IEEE754 спецификацией, которая с ума сойдет если вы A - B - A сократите до -B или (A * B) * C переставите в A * (B * C) т.к. операции неассоциативны. Но есть в современных компиляторах особый режим, который разрешает пренебрегать спекой и граничными значениями (NaN, +-Inf, +-0.0) в таких случаях и смело выполнять оптимизации — это Fast Math (мой PR реквест на добавление такого режима в C# можно найти тут).
Как вы видите в режиме -ffast-math больше нет двух vsubss:
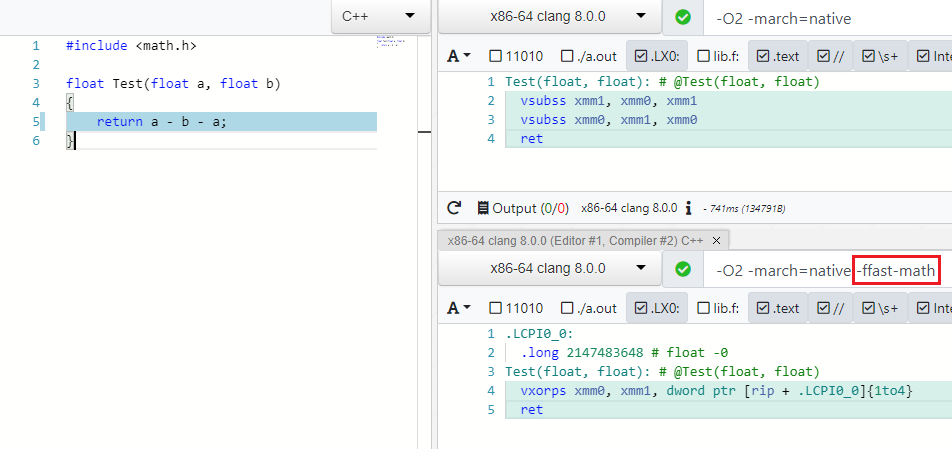
Помимо выражений, оптимизаторы так же принимают в расчет жонглирование математическими функциями из math.h, к примеру, произведение модулей числа Х равно произведению числа Х:
abs(X) * abs(X) => X * XКвадратный корень всегда положителен:
sqrt(X) < Y => false, if Y is negative.
sqrt(X) < 0 => falseЗачем вычислять корень, если можно на этапе компиляции рассчитать квадрат константы справа?:
sqrt(X) > C => X > C * C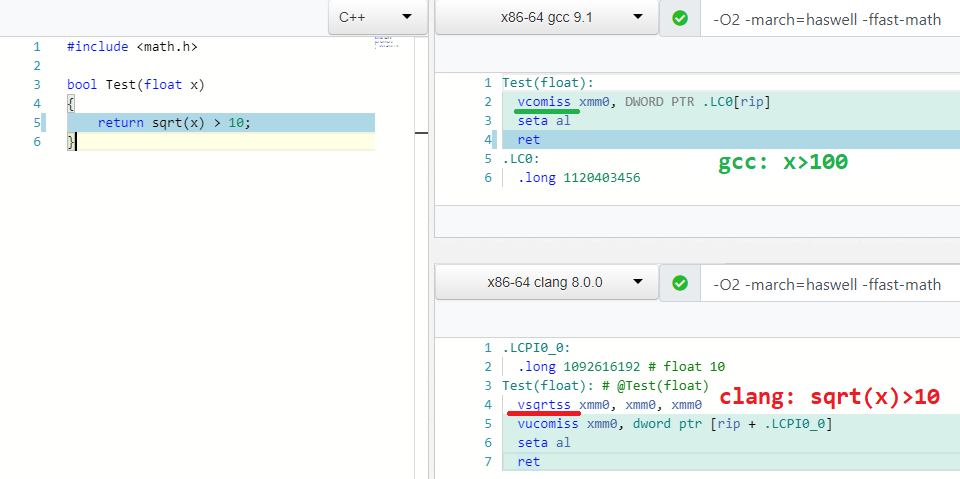
Больше операций с корнями:
sqrt(X) == sqrt(Y) => X == Y
sqrt(X) * sqrt(X) => X
sqrt(X) * sqrt(Y) => sqrt(X * Y)
logN(sqrt(X)) => 0.5*logN(X)Еще немного школьной математики:
expN(X) * expN(Y) -> expN(X + Y)И моя любимая оптимизация:
sin(X) / cos(X) => tan(X)
Много скучных битовых и булевых операций:
((a ^ b) | a) -> (a | b)
(a & ~b) | (a ^ b) --> a ^ b
((a ^ b) | a) -> (a | b)
(X & ~Y) |^+ (~X & Y) -> X ^ Y
A - (A & B) into ~B & A
X <= Y - 1 equals to X < Y
A < B || A >= B -> true
... их очень много!Низкоуровневые оптимизации
Есть набор оптимизации, которые на первый взгляд не имеют смысла с т.з. математики, но более дружественны к железу.
X / 2 => X * 0.5заменяем деление умножением:

Операция умножение над флотами обычно имеет лучшие характеристики (latency/throughput) чем деление. Вот, например, параметры для Intel Haswell:
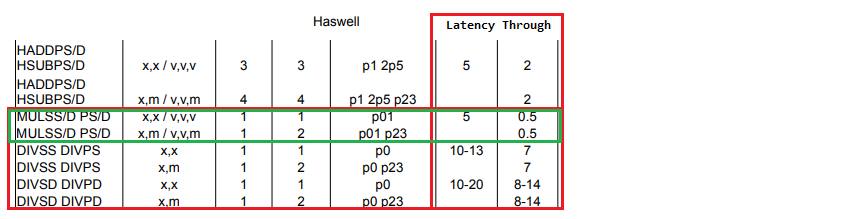
В не fast-math режиме можно применять только если константа является степенью двойки.
Кстати, недавно я попытался добавить такую оптимизацию в C#. Т.е. если вам, к примеру, надо открыть файл с 3Д моделью и уменьшить все координаты в 10 раз, то * 0.1 справится с этим на 20-100% быстрее что может быть существенно.
Тоже самое обоснование для:
X * 2 => X + XСравнение с нулем (test) лучше, чем сравнения с единицей (cmp) — мой PR для деталей — dotnet/coreclr#25458:
X >= 1 => X > 0
X < 1 => X <= 0
X <= -1 => X >= 0
X > -1 => X >= 0А как вам такое:
pow(X, 0.5) => sqrt(x)
pow(X, 0.25) => sqrt(sqrt(X))
pow(X, 2) => X * X ; 1 mul
pow(X, 3) => X * X * X ; 2 mul
Как вы думаете, сколько нужно операций умножения, чтобы посчитать mod(X, 4) или X * X * X * X?
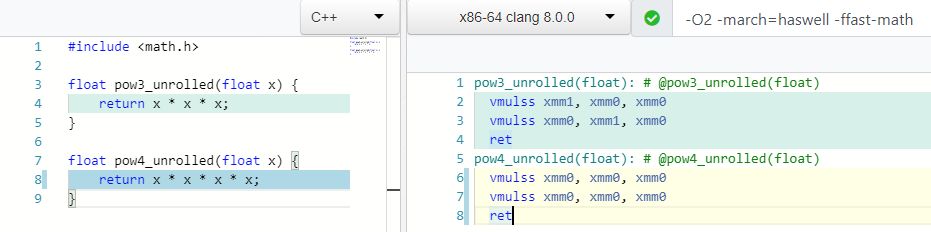
Две! Так же как и для расчета 3ей степени, причем в случае 4 мы используем только один регистр xmm0.
Многие процессоры поддерживают особую инструкцию (FMA), которая позволяет за раз выполнить умножение и сложение, причем с сохранением точности при умножении:
X * Y + Z => fmadd(X, Y, Z)
Еще два моих любимых примера — сворачивание некоторых алгоритмов в одну инструкцию (если процессор ее поддерживает):
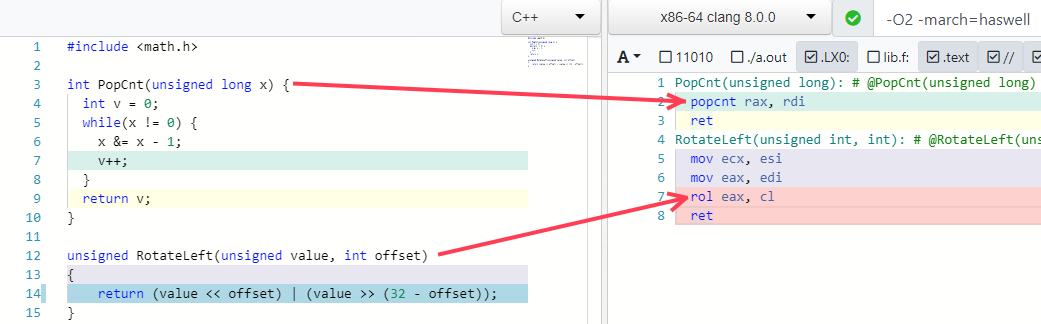
Ловушки для оптимизаций
Я думаю, все понимают, что нельзя так просто бросаться и сокращать выражения по трем причинам:
- Можно сломать код на каких-нибудь граничных значениях, переполнении, скрытых side-эффектов и т.п… Багзилла LLVM содержит много InstCombine багов.
- В идеале, оптимизации должны работать вместе в конкретной последовательности.
- Выражение или его части, которые вы хотите сократить, возможно ещё где-то используются и их сокращение приведет к деградации производительности.
Давайте как раз и рассмотрим пример для последнего пункта (подсмотрел в статье Future Directions for Optimizing Compilers).
Представьте, что у нас есть такой код:
int Foo1(int a, int b) {
int na = -a;
int nb = -b;
return na + nb;
}нам нужно сделать три операции: 0 - a, 0 - b, и na + nb. Но оптимизатор за нас сокращает это до двух — return -(a + b);:
define dso_local i32 @_Z4Foo1ii(i32, i32) {
%3 = add i32 %0, %1 ; a + b
%4 = sub i32 0, %3 ; 0 - %3
ret i32 %4
}Теперь представим, что нам нужно записать промежуточные значения na и nb в глобальные переменные:
int x, y;
int Foo2(int a, int b) {
int na = -a;
int nb = -b;
x = na;
y = nb;
return na + nb;
}Оптимизатор всё так же находит этот паттерн и убирает ненужные (с его точки зрения) операции 0 - a и 0 - b, но по факту-то выходят что они-то нужные! мы записываем результаты этих "ненужных" операций в глобальные переменные! Это приводит к такому коду:
define dso_local i32 @_Z4Foo2ii(i32, i32) {
%3 = sub nsw i32 0, %0 ; 0 - a
%4 = sub nsw i32 0, %1 ; 0 - b
store i32 %3, i32* @x, align 4, !tbaa !2
store i32 %4, i32* @y, align 4, !tbaa !2
%5 = add i32 %0, %1 ; a + b
%6 = sub i32 0, %5 ; 0 - %5
ret i32 %6
}Четыре математические операции вместо трёх! Наш оптимизатор нас подвел и не убедился, что промежуточные выражения, которые он оптимизировал, были ещё кому-то нужны. Теперь посмотрим на вывод C# RuyJIT, в котором нет такой умной оптимизации:
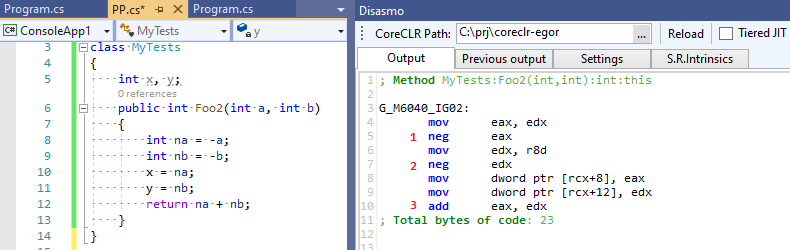
Три операции вместо четырех — C# оказался быстрее C++ :-)!.
А нужны ли такие оптимизации?
Никогда не знаешь как будет выглядеть код после того, как компилятор заинлайнит всё, что сможет и выполнит constant folding, copy propogation, CSE и т.п. — для него откроется совсем другая картина. LLVM IR и .NET IL не привязаны к конкретному языку программирования и нельзя быть уверенным что конкретный/новый ЯП сможет эффективно транслировать себя в IR. Ну и зачем об этом рассуждать если можно на конкретном приложении протестировать производительность с включенным и выключенным InstCombine ;-). Вряд ли это будет внушительная разница, но кто знает.
А что на счет C#?
Как я и говорил, оптимизации выражений, которые мы рассмотрели, скорее всего отсутствуют в C#. Но когда я говорю C# я подразумеваю самый популярный рантайм — CoreCLR и RyuJIT. Но помимо CoreCLR есть еще и другие рантаймы, в том числе использующие LLVM в качестве бэкенда: Mono (см. мой твит), Unity Burst, IL2CPP (через clang) и LILLC — вот к ним можно смело приравнивать результаты C++ с clang. Ребята из Unity даже переписывают внутренний С++ код на C# без потерь в производительности, пруф!
Вот некоторые пипхол оптимизации, которые удалось найти в файле morph.cpp в исходниках CoreCLR по комментариям (их явно немного больше):
*(&X) => X
X % 1 => 0
X / 1 => X
X % Y => X - (X / Y) * Y
X ^ -1 => ~x
X >= 1 => X > 0
X < 1 => X <= 0
X + С1 == C2 => X == C2 - C1
((X + C1) + C2) => (X + (C1 + C2))
((X + C1) + (Y + C2)) => ((X + Y) + (C1 + C2))Еще несколько можно найти в lowering.cpp (низкоуровневые) но в целом RyuJIT очевидно проигрывает тут С++ компиляторам. У RyuJIT немного другие приоритеты — до появления Tiering Compilation ему необходимо было обеспечивать приемлемую скорость компиляции, с чем он справляется на отлично в отличии от С++ компиляторов (вспомните про один только 30к-строчный InstCombine pass в LLVM и в целом почитайте интересный пост "Modern" C++ Lamentations) и куда полезнее развивать оптимизации в области девиртуализации вызовов, устранении боксинга и аллокаций (тот же Object Stack Allocation) — всё это, очевидно, намного важнее, чем сворачивание деления синуса на косинус в тангенс.
Возможно, с появлением Tiering Compilation со временем появится много новых, не критичных ко времени компиляции, оптимизаций для tier1 или даже tier2. Может даже со своим Add-in API и DSL — вы только прочитайте эту статью, в ней Prathamesh Kulkarni добавил оптимизацию выражения в GCC всего в пару строк DSL-я:
(simplify
(plus (mult (SIN @0) (SIN @0))
(mult (COS @0) (COS @0)))
(if (flag_unsafe_math_optimizations)1.
{ build_one_cst (TREE_TYPE (@0)); }))для вот такого выражения из учебника по математике ;-) :
cos^2(X) + sin^2(X) equals to 1 Полезные ссылки
- "Future Directions for Optimizing Compilers", Nuno P. Lopes and John Regehr
- "How LLVM Optimizes a Function", John Regehr
- "The surprising cleverness of modern compilers", Daniel Lemire
- "Adding peephole optimization to GCC", Prathamesh Kulkarni
- "1. C++, C# and Unity", Lucas Meijer
- "Modern" C++ Lamentations", Aras Pranckevičius
- "Provably Correct Peephole Optimizations with Alive", Nuno P. Lopes, David Menendez, Santosh Nagarakatte and John Regehr
Автор: Егор

