Всем привет! Сегодня хотелось бы поговорить о математике. Математика очень интересная наука и она может сильно пригодиться при разработке игр, да и в целом при работе с компьютерной графикой. Многие (особенно новички) просто не знают о том, как она применяется при разработке. Существует множество задач, не требующих глубокого понимания таких понятий как: интегралы, комплексные числа, группы, кольца и др, но благодаря математике вы можете решать многие интересные задачи. В этой статье мы рассмотрим векторы и интегралы. Если интересно, добро пожаловать под кат. Иллюстрирующий Unity проект, как всегда, прилагается.

Векторная математика.
Векторы и векторная математика являются необходимыми инструментами для разработки игр. Многие операции и действия завязаны на ней целиком. Забавно, что для реализации класса, который отображает стрелочку вектора в Unity, уже потребовалось большинство типовых операций. Если вы хорошо разбираетесь в векторной математике данный блок вам будет неинтересен.
Векторная арифметика и полезные функции
Аналитические формулы и прочие детали легко нагуглить, так что не будем тратить на это время. Сами операции будут проиллюстрированы гиф-анимациями ниже.
Важно понимать, что любая точка в сущности является вектором с началом в нулевой точке.
Гифки делались с помощью Unity, так что нужно было бы реализовывать класс, отвечающий за отрисовку стрелочек. Стрелка вектора состоит из трех основных компонент – линии, наконечника и текста с именем вектора. Для отрисовки линии и наконечника я воспользовался LineRenderer. Посмотрим на класс самого вектора:
using System.Collections;
using System.Collections.Generic;
using TMPro;
using UnityEngine;
public class VectorArrow : MonoBehaviour
{
[SerializeField] private Vector3 _VectorStart;
[SerializeField] private Vector3 _VectorEnd;
[SerializeField] private float TextOffsetY;
[SerializeField] private TMP_Text _Label;
[SerializeField] private Color _Color;
[SerializeField] private LineRenderer _Line;
[SerializeField] private float _CupLength;
[SerializeField] private LineRenderer _Cup;
private void OnValidate()
{
UpdateVector();
}
private void UpdateVector()
{
if(_Line == null || _Cup == null) return;
SetColor(_Color);
_Line.positionCount = _Cup.positionCount = 2;
_Line.SetPosition(0, _VectorStart);
_Line.SetPosition(1, _VectorEnd - (_VectorEnd - _VectorStart).normalized * _CupLength);
_Cup.SetPosition(0, _VectorEnd - (_VectorEnd - _VectorStart).normalized * _CupLength);
_Cup.SetPosition(1, _VectorEnd );
if (_Label != null)
{
var dv = _VectorEnd - _VectorStart;
var normal = new Vector3(-dv.y, dv.x).normalized;
normal = normal.y > 0 ? normal : -normal;
_Label.transform.localPosition
= (_VectorEnd + _VectorStart) / 2
+ normal * TextOffsetY;
_Label.transform.up = normal;
}
}
public void SetPositions(Vector3 start, Vector3 end)
{
_VectorStart = start;
_VectorEnd = end;
UpdateVector();
}
public void SetLabel(string label)
{
_Label.text = label;
}
public void SetColor(Color color)
{
_Color = color;
_Line.startColor = _Line.endColor = _Cup.startColor = _Cup.endColor = _Color;
}
}
Так как мы хотим, чтобы вектор был определённой длинны и точно соответствовал точкам, которые мы задаём, то длинна линии рассчитывается по формуле:
_VectorEnd - (_VectorEnd - _VectorStart).normalized * _CupLengthВ данной формуле (_VectorEnd — _VectorStart).normalized – это направление вектора. Это можно понять из анимации с разницей векторов, приняв что _VectorEnd и _VectorStart – это вектора с началом в (0,0,0).
Дальше разберём две оставшиеся базовые операции:
Нахождение нормали (перпендикуляра) и середины вектора – это очень часто встречающиеся задачи при разработке игр. Разберём их на примере размещения подписи над вектором.
var dv = _VectorEnd - _VectorStart;
var normal = new Vector3(-dv.y, dv.x).normalized;
normal = normal.y > 0 ? normal : -normal;
_Label.transform.localPosition = (_VectorEnd + _VectorStart) / 2 + normal * TextOffsetY;
_Label.transform.up = normal;Для того, чтобы разместить текст перпендикулярно вектору нам понадобится нормаль. В 2D графике нормаль находится достаточно просто.
var dv = _VectorEnd - _VectorStart;
var normal = new Vector3(-dv.y, dv.x).normalized;Вот мы и получили нормаль к отрезку.
normal = normal.y > 0? normal: -normal; — эта операция отвечает за то, чтобы текст всегда показывался над вектором.
Дальше остаётся поместить его в середину вектора и поднять по нормали на расстояние, которое будет смотреться красиво.
_Label.transform.localPosition
= (_VectorEnd + _VectorStart) / 2
+ normal * TextOffsetY;В коде использованы локальные позиции, чтобы можно была возможность двигать получившуюся стрелочку.
Но это было про 2D, а что же с 3D?
В 3D плюс-минус всё тоже самое. Отличается только формула нормали, так как нормаль уже берётся не к отрезку, а к плоскости.
В данном примере контролла нормаль к плоскости используется, чтобы сместить конечную точку траектории право, чтобы планету не загораживал интерфейс. Нормаль в 3д графике – это нормализованное векторное произведение двух векторов. Что удобно, в Юнити есть обе эти операции и мы получаем красивую компактную запись:
var right = Vector3.Cross(hit.normal, Vector3.up).normalized;Думаю, многим, кто думает, что математика не нужна и зачем вообще это знать, стало чуть понятнее какие задачи с помощью неё можно решать просто и элегантно. Но это был простой вариант, который должен знать каждый разработчик игр не стажёр. Поднимем планку — поговорим об интегралах.
Интегралы
Вообще у интегралов очень много применений, таких как: физические симуляции, VFX, аналитика и многое другое. Я не готов сейчас детально описывать все. Хочется описать простой и визуально понятный. Поговорим про физику.
Допустим есть задача – двигать объект в определённую точку. К примеру, чтобы при вхождении в определённый триггер, должны вылетать книги с полок. Если вы хотите двигать равномерно и без физики, то задача тривиальна и не требует интегралов, но когда книги выталкивает с полки призрак, такое распределение скорости будет смотреться совсем не так.
Что такое интеграл?
По сути это площадь под кривой. Но что это означает в контексте физики? Допустим у вас есть распределение скорости по времени. В данном случае площадь под кривой – это путь который пройдёт объект, а это как раз то, что нам и нужно.
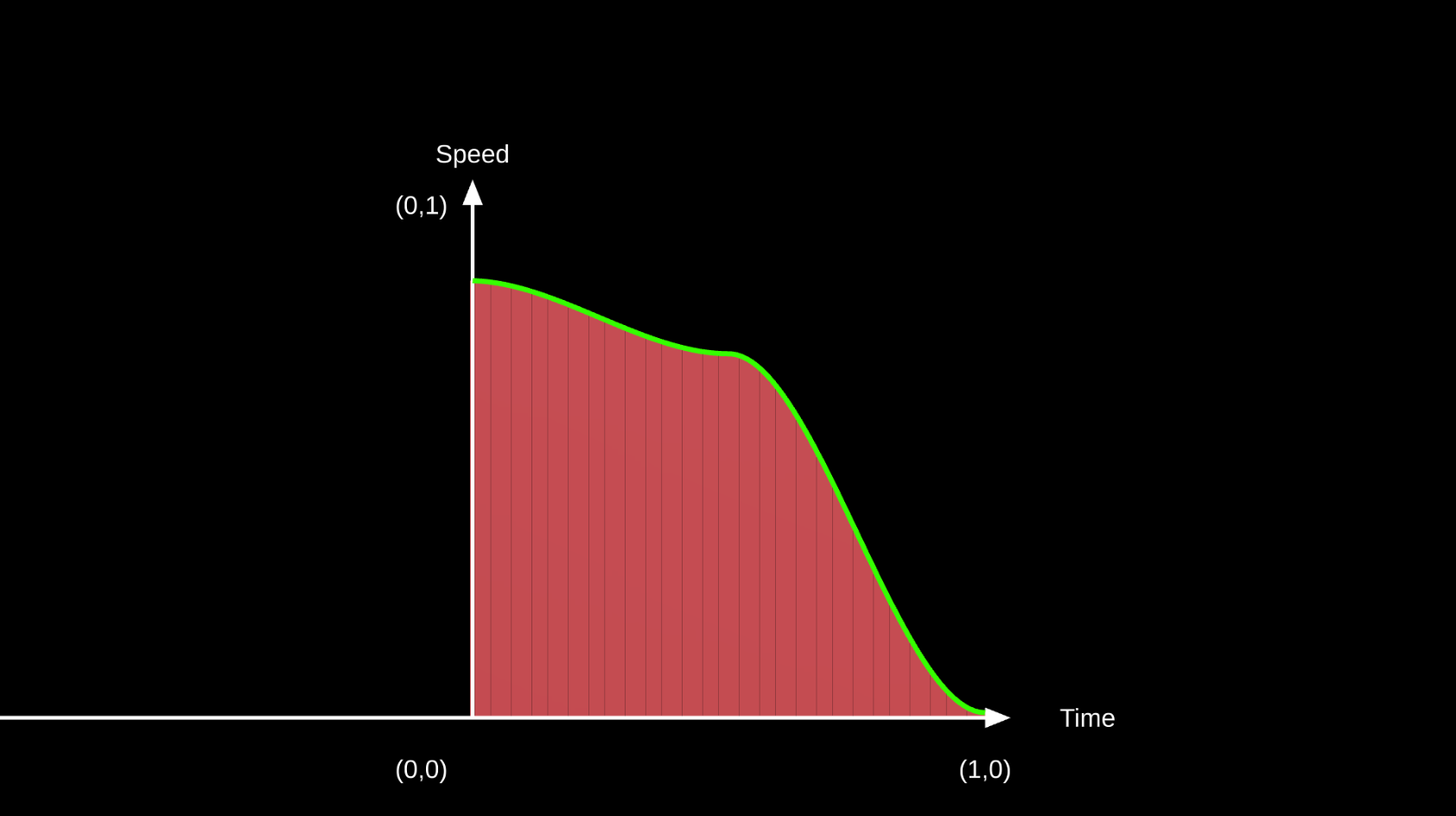
Если перейти от теории к практике, то в Unity есть замечательный инструмент под названием AnimationCurve. С помощью него можно задать распределение скорости с течением времени. Создадим вот такой класс.
using System.Collections;
using UnityEngine;
[RequireComponent(typeof(Rigidbody))]
public class MoveObject : MonoBehaviour
{
[SerializeField] private Transform _Target;
[SerializeField] private GraphData _Data;
private Rigidbody _Rigidbody;
private void Start()
{
_Rigidbody = GetComponent<Rigidbody>();
Move(2f, _Data.AnimationCurve);
}
public void Move(float time, AnimationCurve speedLaw)
{
StartCoroutine(MovingCoroutine(time, speedLaw));
}
private IEnumerator MovingCoroutine(float time, AnimationCurve speedLaw)
{
float timer = 0;
var dv = (_Target.position - transform.position);
var distance = dv.magnitude;
var direction = dv.normalized;
var speedK = distance / (Utils.GetApproxSquareAnimCurve(speedLaw) * time);
while (timer < time)
{
_Rigidbody.velocity = speedLaw.Evaluate(timer / time) * direction * speedK;
yield return new WaitForFixedUpdate();
timer += Time.fixedDeltaTime;
}
_Rigidbody.isKinematic = true;
}
}
Метод GetApproxSquareAnimCurve – это и есть наше интегрирование. Мы делаем его простейшим численным методом, просто идём по значениям фукнции и суммируем их определённое число раз. Я выставил 1000 для верности, в целом можно подобрать оптимальнее.
private const int Iterations = 1000;
public static float GetApproxSquareAnimCurve(AnimationCurve curve)
{
float square = 0;
for (int i = 0; i <= Iterations; i++)
{
square += curve.Evaluate((float) i / Iterations);
}
return square / Iterations;
}Благодаря этой площади мы дальше уже знаем, какое относительное расстояние. А дальше сравнив два пройденных пути мы получаем коэффициент скорости speedK, который отвечает за то, чтобы мы прошли заданное расстояние.
Можно заметить, что объекты не совсем совпадают, это связано с ошибкой float. В целом можно пересчитать тоже самое в decimal, а потом перегнать в float для большей точности.
Собственно на этом на сегодня всё. Как всегда в конце ссылка на GitHub проект, в котором все исходники по данной статье. И с ними можно поиграться.
Если статья зайдёт — сделаю продолжение в котором расскажу уже про применение чуть более сложных понятий, таких как комплексные числа, поля, группы и другое.
Автор: DyadichenkoGA




