«Паттерны» функционального программирования

Многие люди представляют функциональное программирование как нечто очень сложное и «наукоемкое», а представителей ФП-сообщества – эстетствующими философами, живущими в башне из слоновой кости.

До недавнего времени такой взгляд на вещи действительно был недалек от истины: говорим ФП, подразумеваем Хаскель и теорию категорий. В последнее время ситуация изменилась и функциональная парадигма набирает обороты в web-разработке, не без помощи F#, Scala и React. Попробуем взглянуть на «паттерны» функционального программирования, полезные для решения повседневных задач с точки зрения ООП – парадигмы.

ООП широко распространено в разработке прикладного ПО не одно десятилетие. Все мы знакомы с SOLID и GOF. Что будет их функциональным эквивалентом?.. Функции! Функциональное программирование просто «другое» и предлагает другие решения.

Основные принципы функционального проектирования (дизайна)

Функции как объекты первого класса

В отличие от «классического» ООП (первые версии C++, C#, Java) функции в ФП представляют собой самостоятельные объекты и не должны принадлежать какому-либо классу. Удобно представлять функцию как волшебный железнодорожный тоннель: подаете на вход яблоки, а на выходе получаете бананы (apple -> banana).

Синтаксис F# подчеркивает, что функции и значения равны в правах:

let z = 1
let add = x + y // int -> int ->int

Композиция как основной «строительный материал»

Если у нас есть две функции, одна преобразующая яблоки в бананы (apple -> banana), а другая бананы в вишни (banana -> cherry), объединив их мы получим функции преобразования яблок в вишни (apple -> cherry). С точки зрения программиста нет разницы получена эта функция с помощью композиции или написана вручную, главное – ее сигнатура.

Композиция применима как на уровне совсем небольших функций, так и на уровне целого приложения. Вы можете представить бизнес-процесс, как цепочку вариантов использования (use case) и скомпоновать их в функцию httpRequest -> httpResponse. Конечно это возможно только для синхронных операций, но для асинхронных есть реактивное функциональное программирование, позволяющее сделать тоже самое.

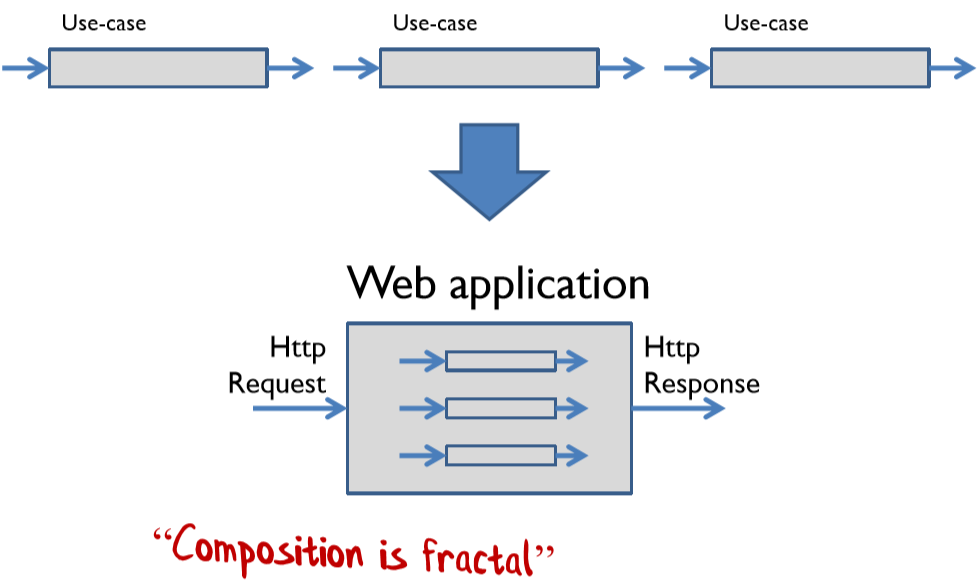
Можно представлять себе композицию функций как фрактал. Определение фрактала в строгом смысле не совпадает с определением композиции. Представляя фрактал вы можете визуализировать как ваш control flow состоит из скомпонованных функций, состоящих из скомпонованных функций, состоящих из…

Шаблон компоновщик (Composite) в ООП тоже можно представлять себе «фракталом», но компоновщик работает со структурами данных, а не преобразованиями.

Типы != классы

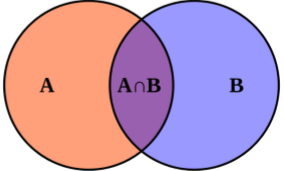У системы типов в ФП больше общего с теорией множеств, чем с классами из ООП. int – это тип. Но тип не обязательно должен быть примитивом. Customer – это тоже тип. Функции могут принимать на вход и возвращать функции. int -> int – тоже тип. Так что «тип» — это название для некоторого множества.

Типы тоже можно компоновать. Большая часть функциональных ЯП работает с алгебраической системой типов, отличающейся от системы классов в ООП.

Перемножение (логическое «и», record type в F#)

На первый взгляд это может показаться странным, однако в этом есть смысл. Если взять множество людей и множество дат, «перемножив» их мы получим множество дней рождений.

type Birthday = Person * Date

Сложение (логическое «или», discriminated union type в F#)

type PaymentMethod =  
| Cash
| Cheque of ChequeNumber
| Card of CardType * CardNumber

Discriminated union – сложное название. Проще представлять себе этот тип как выбор. Например, вы можете на выбор оплатить товар наличными, банковским переводом или с помощью кредитной карты. Между этими вариантами нет ничего общего, кроме того, все они являются способом оплаты.

Однажды нам пригодились «объединения» для моделирования предметной модели.
Entity Framework умеет работать с такими типами из коробки, нужно лишь добавить id.

Стремление к «полноте»

Давайте рассмотрим функцию «разделить 12 на». Ее сигнатура int -> int и это ложь! Если мы подадим на вход 0, функция выбросит исключение. Вместо этого мы можем заменить сигнатуру на NonZeroInteger -> int или на int -> int option.

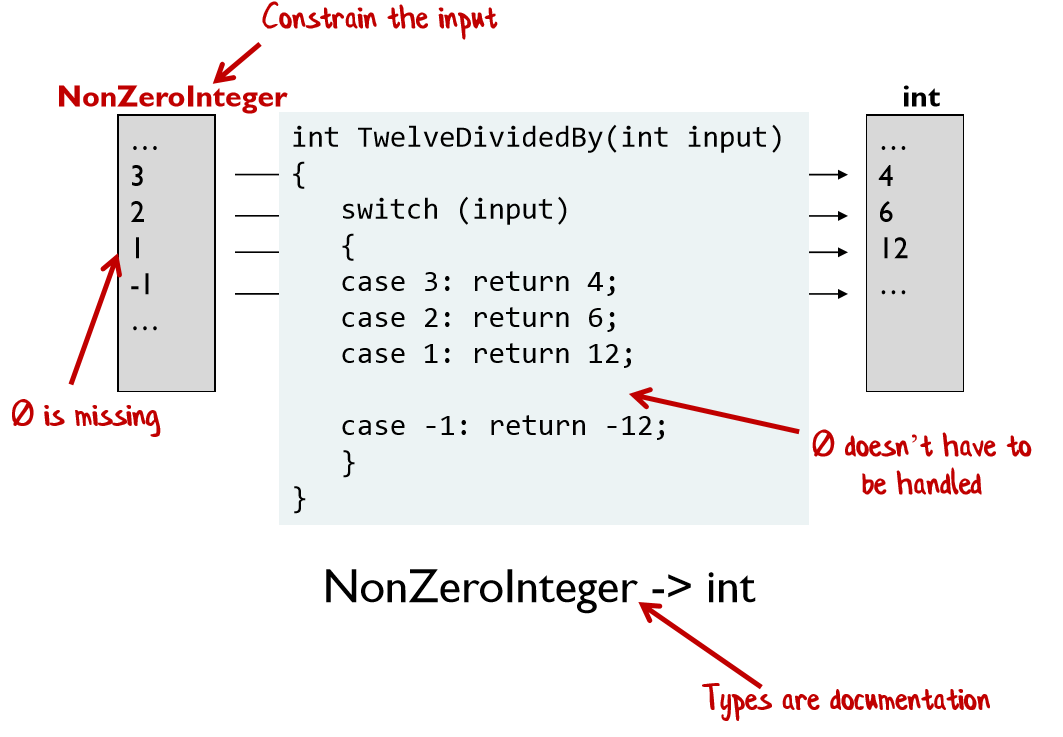
ФП подталкивает вас к более строгому и полному описанию сигнатур функций. Если функции не выбрасывают исключений вы можете использовать сигнатуру и систему типов в качестве документации. Вы также можете использовать систему типов для создания предметной модели (Domain Model) и описания бизнес-правил (Business Rules). Таким образом можно гарантировать, что операции не допустимые в реальном мире не будут компилироваться в приложении, что дает более надежную защиту, чем модульные тесты. Подробнее об этом подходе вы можете прочитать в отдельной статье.

Функции в качестве аргументов

Хардкодить данные считается дурным тоном в программирование, вместо этого мы передаем их в качестве параметров (аргументов методов). В ФП мы идем дальше. Почему бы не параметризировать и поведение?

Вместо функции с одним аргументом опишем функцию с двумя. Теперь не важно, что это за список и куда мы выводим данные (на консоль или в лог).

let printList anAction aList =
    for i in aList do
        anAction i

Пойдем дальше. Рассмотрим императивный пример на C#. Очевидно, что в данном коде присутствует дублирование (одинаковые циклы). Для того чтобы устранить дублирование нужно выделить общее и выделить общее в функцию:

public static int Product(int n)
{     
    int product = 1; // инициализация
    for (int i = 1; i <= n; i++) // цикл
    {
        product *= i; // действие
    }

    return product; // возвращаемое значение
} 
 
public static int Sum(int n) 
{
    int sum = 0; // инициализация
    for (int i = 1; i <= n; i++) // цикл
    {
        sum += i;
    }

    return sum; // возвращаемое значение
} 

В F# для работы с последовательностями уже есть функция fold:

let product n =
    let initialValue = 1
    let action productSoFar x = productSoFar * x

[1..n] |> List.fold action initialValue 
 
let sum n =
    let initialValue = 0
    let action sumSoFar x = sumSoFar+x

[1..n] |> List.fold action initialValue

Но, позвольте, в C# есть Aggregate, который делает тоже самое! Поздравляю, LINQ написан в функциональном стиле :)

Рекомендую цикл статей Эрика Липперта о монадах в C#. С десятой части начинается объяснение «монадической» природы SelectMany

Функции в качестве интерфейсов

Допустим у нас есть интерфейс.

interface IBunchOfStuff
{
    int DoSomething(int x);
    string DoSomethingElse(int x); // один интерфейс - одно дело
    void DoAThirdThing(string x); // нужно разделить
} 

Если взять SRP и ISP и возвести их в абсолют все интерфейсы будут содержать только одну функцию.

interface IBunchOfStuff
{
    int DoSomething(int x);
} 

Тогда это просто функция int -> int. В F# не нужно объявлять интерфейс, чтобы сделать функции взаимозаменяемыми, они взаимозаменяемы «из коробки» просто по своей сигнатуре. Таким образом паттерн «стратегия» реализуется простой передачей функции в качестве аргумента другой функции:

let DoSomethingWithStuff strategy x =
    strategy x

Паттерн «декоратор» реализуется с помощью композиции функций

let isEvenWithLogging = log >> isEven >> log  // int -> bool

Здесь автор для простоты изложения опускает вопросы семантики. При моделировании реальных предметных моделей одной сигнатуры функции не всегда достаточно.

Каррирование и частичное применение

Итак, использую одну только композицию мы можем проектировать целые приложения. Плохие новости: композиция работает только с функциями от одного параметра. Хорошие новости: в ФП все функции являются функциями от одного параметра.

Обратите внимание, сигнатура int -> int -> int не содержит скобок не случайно. Можно воспринимать сложение, как функцию от двух аргументов типа int, возвращающую значение типа int или как функцию от одного аргумента, возвращающую функциональный тип int -> int. Возвращаемая функция будет называться сумматор по основанию n, где n — число переданное аргументом в первую функцию. Повторив эту операцию рекурсивно можно функцию от любого числа аргументов преобразовать в функции от одного аргумента.

Такие преобразования возможны не только для компилируемых функций в программировании, но и для математических функций. Возможность такого преобразования впервые отмечена в трудах Готтлоба Фреге, систематически изучена Моисеем Шейнфинкелем в 1920-е годы, а наименование получило по имени Хаскелла Карри — разработчика комбинаторной логики, в которой сведение к функциям одного аргумента носит основополагающий характер.

Возможность преобразования функций от многих аргументов к функции от одного аргумента естественна для функциональных ЯП, поэтому компилятор не будет против, если вы передадите только одно значения для вычисления суммы.

let three = 1 + 2 
let three = (+) 1 2 
let three = ((+) 1) 2 
let add1 = (+) 1  
let three = add1 2 

Это называется частичным применением. В функциональных ЯП частичное применение заменяет принцип инъекции зависимостей (Dependency Injection)

// эта функция требует зависимость
let getCustomerFromDatabase connection (customerId:CustomerId) =
    from connection
    select customer
    where customerId = customerId
 
// а эта уже нет
let getCustomer1 = getCustomerFromDatabase myConnection 

Продолжения (continuations)

Зачастую решения, закладываемые в реализацию, оказываются не достаточно гибкими. Вернемся к примеру с делением. Кто сказал, что я хочу, чтобы функция выбрасывала исключения? Может быть мне лучше подойдет «особый случай»

int Divide(int top, int bottom) 
{
    if (bottom == 0)
    {
        // кто решил, что нужно выбросить исключение?
        throw new InvalidOperationException("div by 0");
    }
    else 
    {
        return top/bottom;
    }
}

Вместо того, чтобы решать за пользователя, мы можем предоставить решение ему:

void Divide(int top, int bottom, Action ifZero, Action<int> ifSuccess) 
{
    if (bottom == 0)
    {
        ifZero();
    }
    else
    {
        ifSuccess( top/bottom );
     }
}
 

Если вы когда-нибудь писали асинхронный код, то наверняка знакомы с «пирамидой погибели» (Pyramid Of Doom)

Продолжения позволяют исправить этот код и избавиться от уровней вложенности. Для этого необходимо инкапуслировать условный переход в функцию:

let ifSomeDo f opt =
    if opt.IsSome then
        f opt.Value
    else
        None

И переписать код, используя продолжения

let example input =
    doSomething input
    |> ifSomeDo doSomethingElse
    |> ifSomeDo doAThirdThing
    |> ifSomeDo (fun z -> Some z)

Монады

Монады – это одно из «страшных» слов ФП. В первую очередь, из-за того, что обычно объяснения начинаются с теории категорий. Во вторую — из-за того что «монада» — это очень абстрактное понятие, не имеющее прямой аналогии с объектами реального мира. Я большой сторонник подхода «от частного к общему». Поняв практическую пользу на конкретном примере проще двигаться дальше к более полному и абстрактному определению.

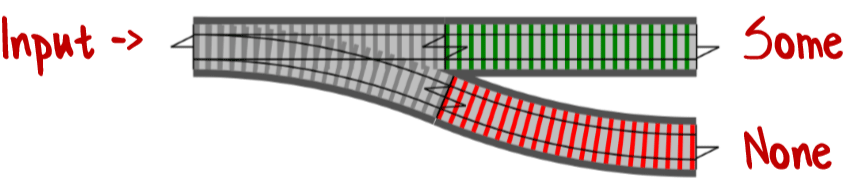
Зная о «продолжениях», вернемся к аналогии с рельсами и тоннелем. Функцию, в которую передаются аргумент и два «продолжения» можно представить как развилку.

Но такие функции не компонуются :(

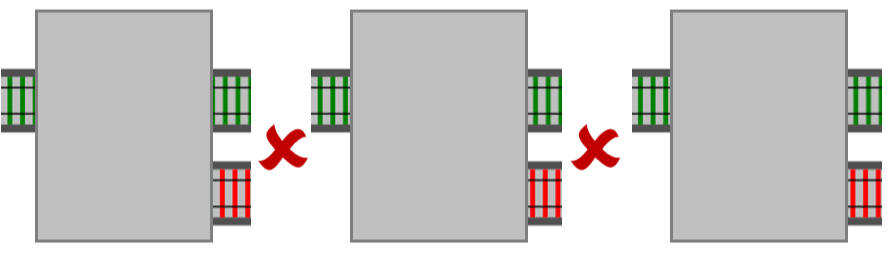
На помощь приходит функция bind

let bind nextFunction optionInput =
    match optionInput with
    // передаем результат выполнения предыдущей функции в случае успеха
    | Some s -> nextFunction s
    // или просто пробрасываем значение None дальше
    | None -> None

Код пирамиды погибели может быть переписан с помощью bind

// было
let example input =
    let x = doSomething input
    if x.IsSome then
        let y = doSomethingElse (x.Value)
        if y.IsSome then
            let z = doAThirdThing (y.Value)
            if z.IsSome then
                let result = z.Value
                Some result
            else
               None
        else 
            None 
    else
        None 

// стало
let bind f opt =
    match opt with
        | Some v -> f v
        | None -> None

let example input =
    doSomething input
        |> bind doSomethingElse
        |> bind doAThirdThing
        |> bind (fun z -> Some z)

Кстати, это называется «monadic bind». Скажите своим друзьям, любителям хаскеля, что вы знаете, что такое «monadic bind» и вас примут в тайное общество:)

Bind можно использовать для сцепления асинхронных операций (промисы в JS устроены именно так)

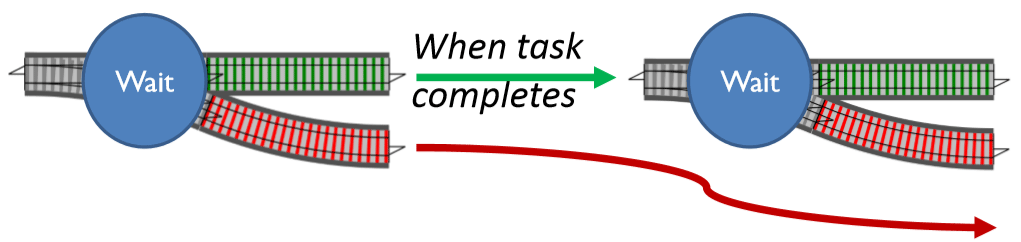
Bind для обработки ошибок

Если у вас появилось смутное ощущение, что дальше идет описание монады Either, так оно и есть

Рассмотрим код на C#. Он выглядит достаточно хорошо: все кратко и понятно. Однако в нем отсутствует обработка ошибок. Действительно, что может пойти не так?

string UpdateCustomerWithErrorHandling() 
{
    var request = receiveRequest();
    validateRequest(request);
    canonicalizeEmail(request);
    db.updateDbFromRequest(request);
    smtpServer.sendEmail(request.Email) 
    return "OK";
} 

Мы все знаем, что обрабатывать ошибки нужно. Добавим обработку.

string UpdateCustomerWithErrorHandling() 
{
    var request = receiveRequest();
    var isValidated = validateRequest(request);
    if (!isValidated) 
    {
        return "Request is not valid"
    }
    
    canonicalizeEmail(request);
    try 
    {
         var result = db.updateDbFromRequest(request);
         if (!result) 
        {
           return "Customer record not found"
        }
    }
    catch
    {
        return "DB error: Customer record not updated"
    } 
 
    if (!smtpServer.sendEmail(request.Email))
    {
        log.Error "Customer email not sent"
    } 
 
    return "OK";
} 

Вместо шести понятных теперь 18 не понятных строчек. Это 200% дополнительных строчек кода. Кроме того, линейная логика метода теперь зашумлена ветвлениями и ранними выходами.

С помощью bind можно абстрагировать логику обработки ошибок. Вот так будет выглядеть метод без обработки ошибок, если его переписать на F#:

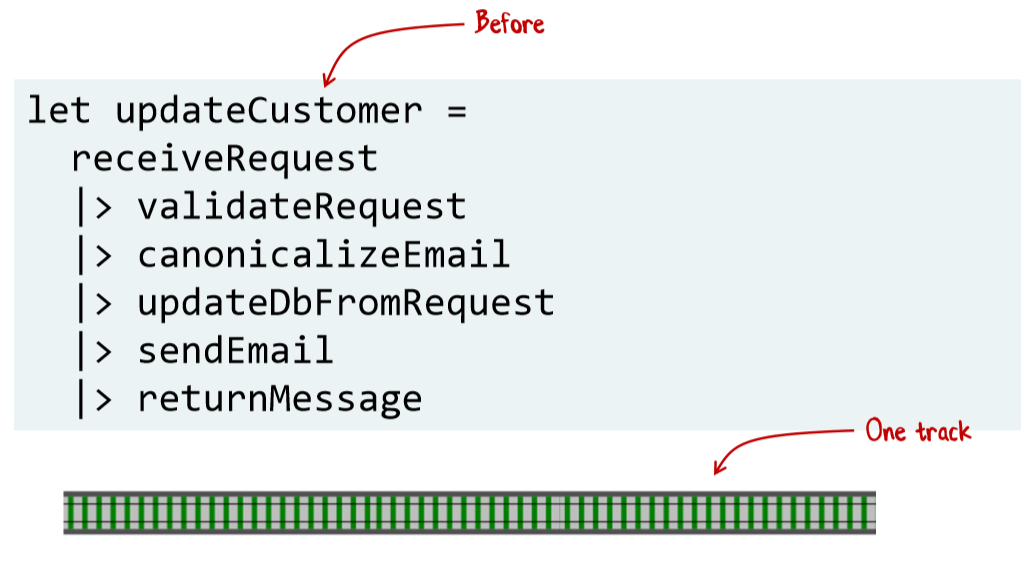
А вот этот код но уже с обработкой ошибок:

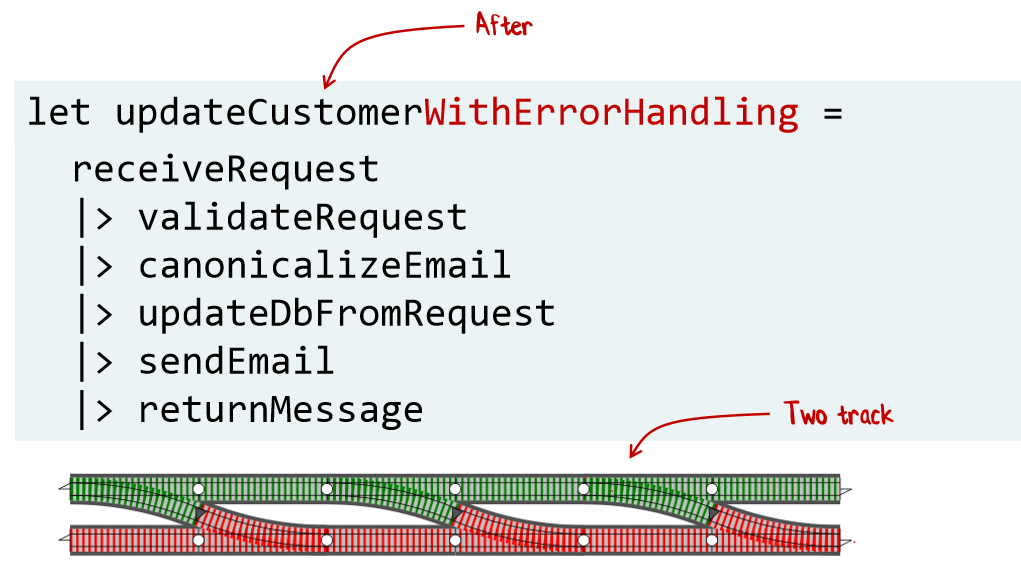
Более подробно эта тема раскрыта в отдельном докладе.

Функторы

Мне не очень понравилось описание функторов у Скотта. Прочитайте лучше статью «Функторы, аппликативные функторы и монады в картинках»

Моноиды

К сожалению, для объяснения моноидов не подходят простые аналогии. Приготовьтесь к математике.

Я предупредил, итак, математика

• 1 + 2 = 3
• 1 + (2 + 3) = (1 + 2) + 3
• 1 + 0 = 1
  0 + 1 = 1

И еще немного

• 2 * 3 = 6
• 2 * (3 * 4) = (2 * 3) * 4
• 1 * 2 = 2
  2 * 1 = 2

Что общего между этими примерами?

1. Есть некоторые объекты, в данном случае числа, и способ их взаимодействия. Причем результат взаимодействия — это тоже число (замкнутость).
2. Порядок взаимодействия не важен (ассоциативность).
3. Кроме того, есть некоторый специальный элемент, взаимодействие с которым не меняет исходный объект (нейтральный элемент).

За более строгим определением обратитесь к википедии. В рамках статьи обсуждается лишь несколько примеров применения моноидов на практике.

Замкнутость

Дает возможность перейти от попарных операций к операциям на списках

1 * 2 * 3 * 4
[ 1; 2; 3; 4 ] |> List.reduce (*)

Ассоциативность

Применение принципа «разделяй и властвуй», «халявная» параллелизация. Если у нашего процессора 2 ядра и нам нужно рассчитать значение 1 + 2 + 3 + 4. Мы можем вычислить 1 + 2 на первом ядре, а 3 + 4 — на втором, а результат сложить. Больше последовательных вычислений — больше ядер.

Нейтральный элемент

С reduce есть несколько проблем: что делать с пустыми списками? Что делать, если у нас нечетное количество элементов? Правильно, добавить в список нейтральный элемент.

Кстати, в математике часто встречается определение моноида как полугруппы с нейтральным элементом. Если нейтральный элемент отсутствует, то можно попробовать его доопределить, чтобы воспользоваться преимуществами моноида.

Map / Reduce

Если ваши объекты — не моноиды, попробуйте преобразовать их. Знаменитая модель распределенных вычислений Google — не более чем эксплуатация моноидов.

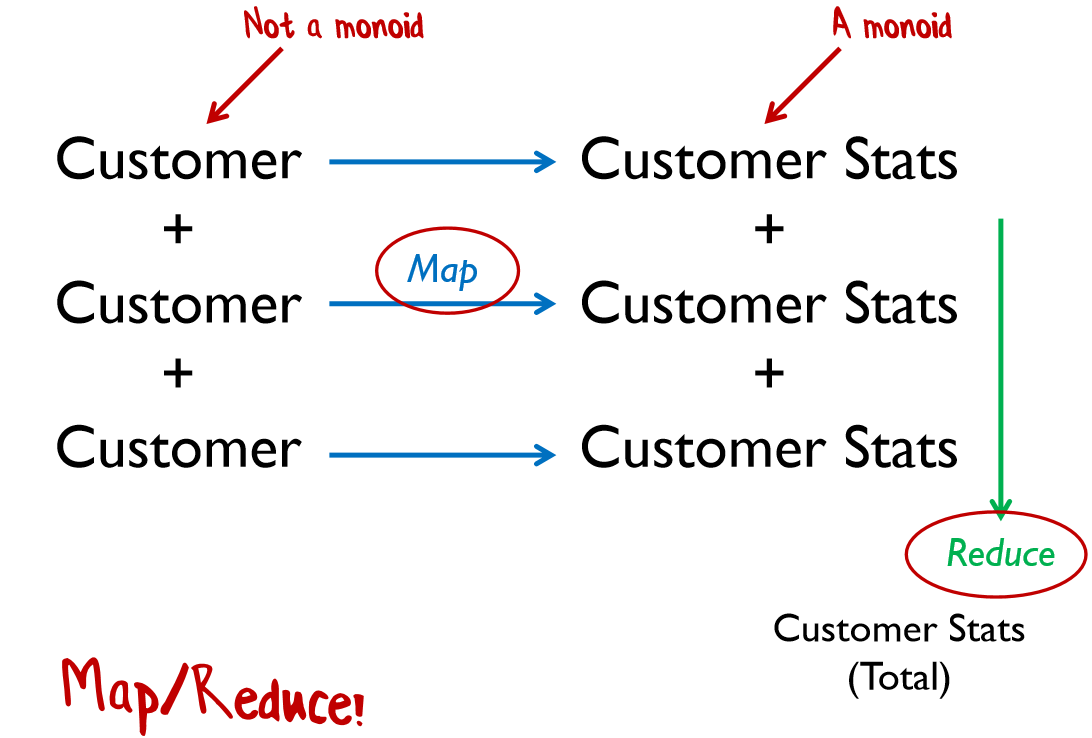
Эндоморфизмы

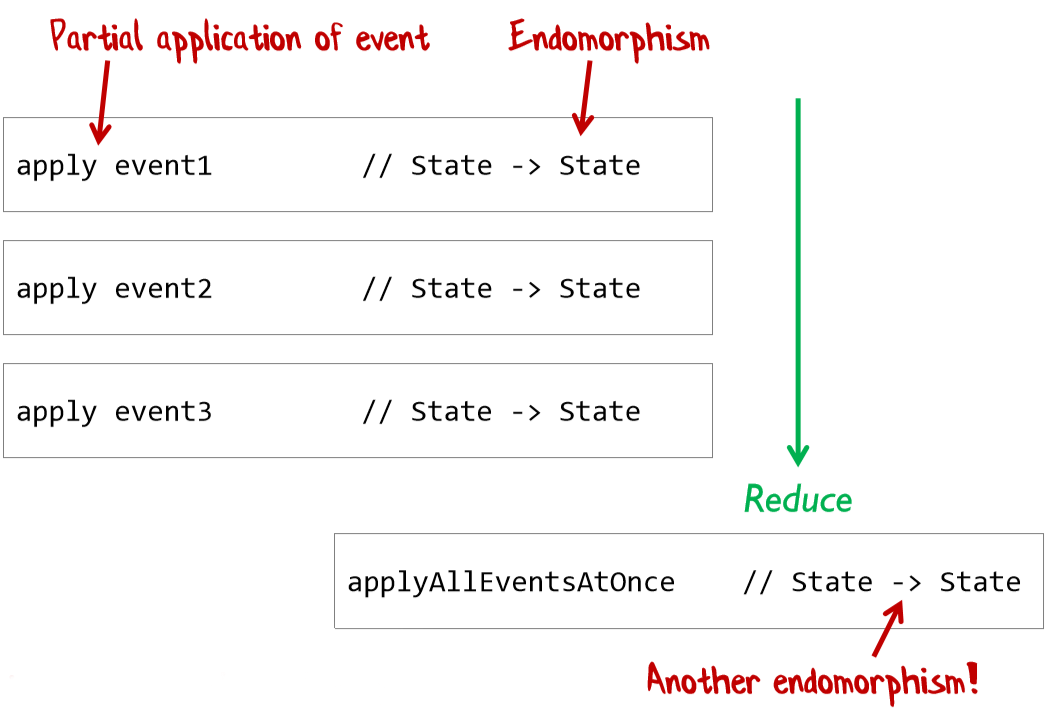
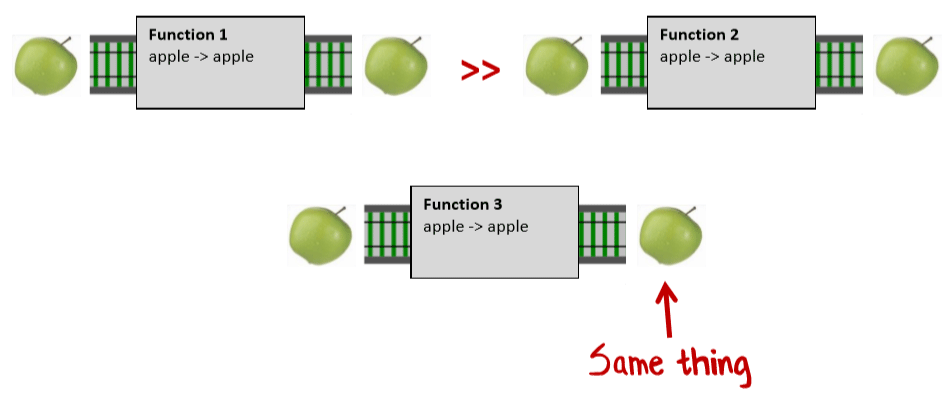Функции с одинаковым типом входного и выходного значения являются моноидами и имеют специальное название — «эндоморфизмы» (название заимствовано из теории категорий). Что более важно, функции, содержащие эндоморфизмы могут быть преобразованы к эндоморфизмам с помощью частичного применения.

Грег Янг открыто заявляет, что Event Sourcing — это просто функциональный код. Flux и unidirectional data flow, кстати тоже.

Монады VS моноиды

Монады являются моноидами, ведь как известно, монада — это всего лишь моноид в категории эндофункторов, а монадические законы — не более чем определение моноида в контексте продолжений.

Кстати, бастион ООП — GOF тоже содержит монады. Паттерн «интерпретатор» — это так называемая свободная монада.

Автор: Максим Аршинов

Источник