Главная

Безытеративное обучение однослойного персептрона. Задача классификации

2017-07-15 в 7:40, admin, рубрики: .net, C#, математика, машинное обучение, нейронные сети, персептрон

Я продолжаю цикл статей по разработке метода безытеративного обучения нейронных сетей. В этой статье будем обучать однослойный персептрон с сигмоидальной активационной ф-ей. Но этот метод можно применить для любых нелинейных биективных активационных ф-й с насыщением и первые производные которых симметричны относительно оси OY.

В прошлой статье мы рассмотрели метод обучения основанный на решении СЛАУ, решать ее мы не будем т.к. это слишком трудоемкий процесс. Сейчас нас интересует из этого метода только вектор «B», в этом векторе отражено насколько важен тот или иной признак для классификации.

$\B={b_1...b_m}; \b_k=-sum_{i=1}^nx_k^i cdot y^i; \k in [1,m];$

И тут из-за того, что имеется активационная ф-я с насыщением можно выразить веса как:

$\W={w_1,...,w_m}; \W=Kcdot B;$

Первое, что необходимо сделать — это заменить $y^i$ на $t^i$ . Т.к. в задачи классификации «y» может быть либо 1(принадлежит), либо 0(не принадлежит). То t должно быть либо 1, либо -1. Отсюда $t^i=2cdot y^i-1$ . Теперь

$b_k=-sum_{i=1}^nx^i_kcdot t^i;$

Теперь выразим коэффициент «K» как дробь, где в числителе функция, обратная ф-и активации от 0.99(от единицы взять нельзя т.к. будет +бесконечность), а в знаменателе усредненное значение модулей всех элементов входящих в выборку(вероятно, можно использовать квадратный корень из усредненной энергии). И умножается все это на -1.

Итоговая формула получается:

$w_k=frac{ncdot mcdot f^{-1}_a(0.99)cdot sum_{i=1}^nx^i_kcdot t^i}{sum^n_{i=1}sum^m_{j=1}|x^i_j|};$

Для сигмоиды, которая имеет вид $f_a(x)=frac{1}{1+exp(-betacdot x)}$ , обратная ф-я — $f^{-1}_a(x)=-frac{ln(frac{1}{x}-1)}{beta}$ , при $beta=1; f^{-1}_a(0.99)=4.6$

*Небольшая проверка
Пусть есть две пары $x^1={1,0,1,0}; y^1=1; x^2={0.7,1,0.1,1}; y^2=0;$ . Рассчитаем веса по формуле приведенной выше:

$\w_1=-1.83; \w_2=-6.1; \w_3=5.49; \w_4=-6.1;$

Теперь «прогоним» наши вектора через получившийся нейрон, напомню формулу отклика нейрона:

$y(x)=f_a(sum_{i=1}^nw_ix_i);$

Первый вектор дал результат 0.997, второй — $2cdot 10^{-6}$ , что очень похоже на правду.

*Тестирование

Для тестирования была взята обучающая выборка 2 сигнала без шума, 1 и 2 Гц, 200 отсчетов. Одному герцу соответствует отклик НС {0,1}, двум {1,0}.

Во время тестирования распознавался сигнал + гауссов шум. ОСШ = 0.33

Ниже представлено распознавание:
1Гц, самый хороший результат

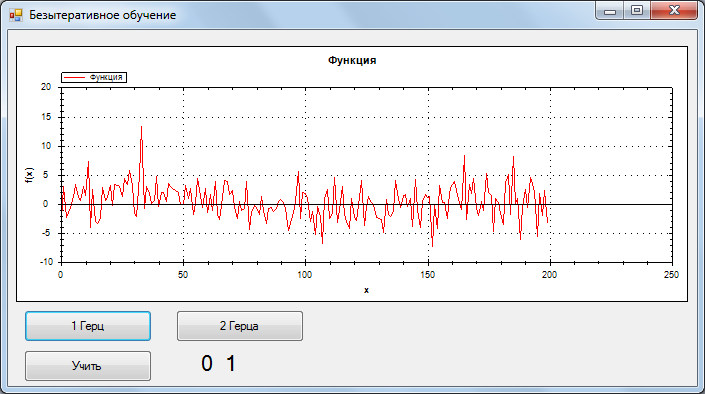
2 Гц, самый хороший результат
Безытеративное обучение однослойного персептрона. Задача классификации - 16
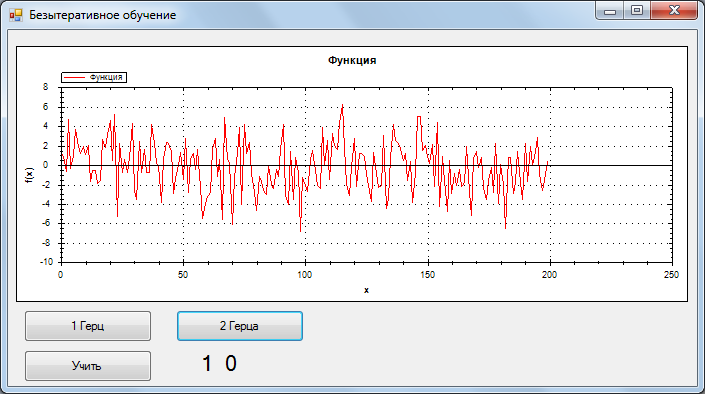
1 Гц, самый плохой результат

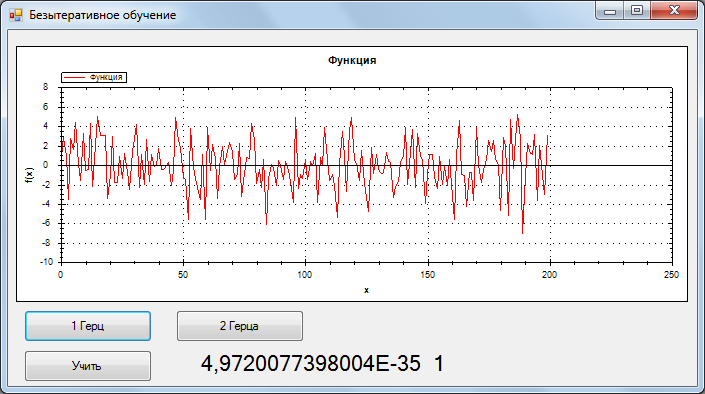
Учитывая, то что точность очень высокая(тестировал и на других сигналах). Я предполагаю, что данный метод сводит функцию ошибки в глобальный минимум.

Код обучения:

	public void Train(Vector[] inp, Vector[] outp)
		{
			OutNew = new Vector[outp.Length];
			In = new Vector[outp.Length];
			Array.Copy(outp, OutNew, outp.Length);
			Array.Copy(inp, In, inp.Length);
			
			
			for (int i = 0; i < OutNew.Length; i++)
			{
				OutNew[i] = 2*OutNew[i]-1;
			}
			
			
			K = 4.6*inp[0].N*inp.Length;
			
			double summ = 0;
			
			for (int i = 0; i < inp.Length; i++)
			{
				summ += Functions.Summ(MathFunc.abs(In[i]));
			}
			
			K /= summ;
			
			
			Parallel.For(0, _neurons.Length, LoopTrain);
		}
		
		
		void LoopTrain(int i)
		{
			
			for (int k = 0; k < In[0].N; k++) {
				
				for (int j = 0; j < OutNew.Length; j++)
				{
					_neurons[i].B.Vecktor[k] += OutNew[j].Vecktor[i]*In[j].Vecktor[k];
				}
			
			}
			
			_neurons[i].W = K*_neurons[i].B;
		}

В дальнейших статьях планирую рассмотреть, обучение многослойных сетей, генерацию сетей с оптимальной архитектурой и обучение сверточных сетей.

Автор: Понимаш Захар Алексеевич

Источник