В настоящее время огромное количество задач требует большой производительности систем. Бесконечно увеличивать количество транзисторов на кристалле процессора не позволяют физические ограничения. Геометрические размеры транзисторов нельзя физически уменьшать, так как при превышении возможно допустимых размеров начинают проявляться явления, которые не заметны при больших размерах активных элементов — начинают сильно сказываться квантовые размерные эффекты. Транзисторы начинают работать не как транзисторы.
А закон Мура здесь ни при чем. Это был и остается законом стоимости, а увеличение количества транзисторов на кристалле — это скорее следствие из закона. Таким образом, для того, чтобы увеличивать мощность компьютерных систем приходится искать другие способы. Это использование мультипроцессоров, мультикомпьютеров. Такой подход характеризуется большим количеством процессорных элементов, что приводит к независимому исполнение подзадач на каждом вычислительном устройстве.
Параллельные методы обработки:
| Источник параллелизма | Ускорение | Усилие программиста | Популярность |
|---|---|---|---|
| Множество ядер | 2х-128х | Умеренное | Высокая |
| Множество машин | 1х-Бесконечность | Умеренно-Высокое | Высокая |
| Векторизация | 2х-8х | Умеренное | Низкая |
| Графические адаптеры | 128х-2048х | Высокое | Низкая |
| Сопроцессор | 40х-80х | Умеренно-высокое | Чрезвычайно-низкая |
Способов для повышения эффективности систем много и все довольно различны. Одним из таких способов является использование векторных процессоров, которые в разы повышают скорость вычислений. В отличие от скалярных процессоров, которые обрабатывают один элемент данных за одну инструкцию (SISD), векторные процессоры способны за одну инструкцию обрабатывать несколько элементов данных (SIMD). Большинство современных процессоров являются скалярными. Но многие задачи, которые они решают, требуют большого объема вычислений: обработка видео, звука, работа с графикой, научные расчеты и многое другое. Для ускорения процесса вычислений производители процессоров стали встраивать в свои устройства дополнительные потоковые SIMD-расширения.
Соответственно при определенном подходе программирования стало возможным использование векторной обработки данных в процессоре. Существующие расширения: MMX, SSE и AVX. Они позволяют использовать дополнительные возможности процессора для ускоренной обработки больших массивов данных. При этом векторизация позволяет добиться ускорения без явного параллелизма. Т.е. он есть с точки зрения обработки данных, но с точки зрения программиста это не требует каких-либо затрат на разработку специальных алгоритмов для предотвращения состояния гонки или синхронизации, а стиль разработки не отличается от синхронного. Мы получаем ускорение без особых усилий, почти совершенно бесплатно. И в этом нет никакой магии.
Что такое SSE?
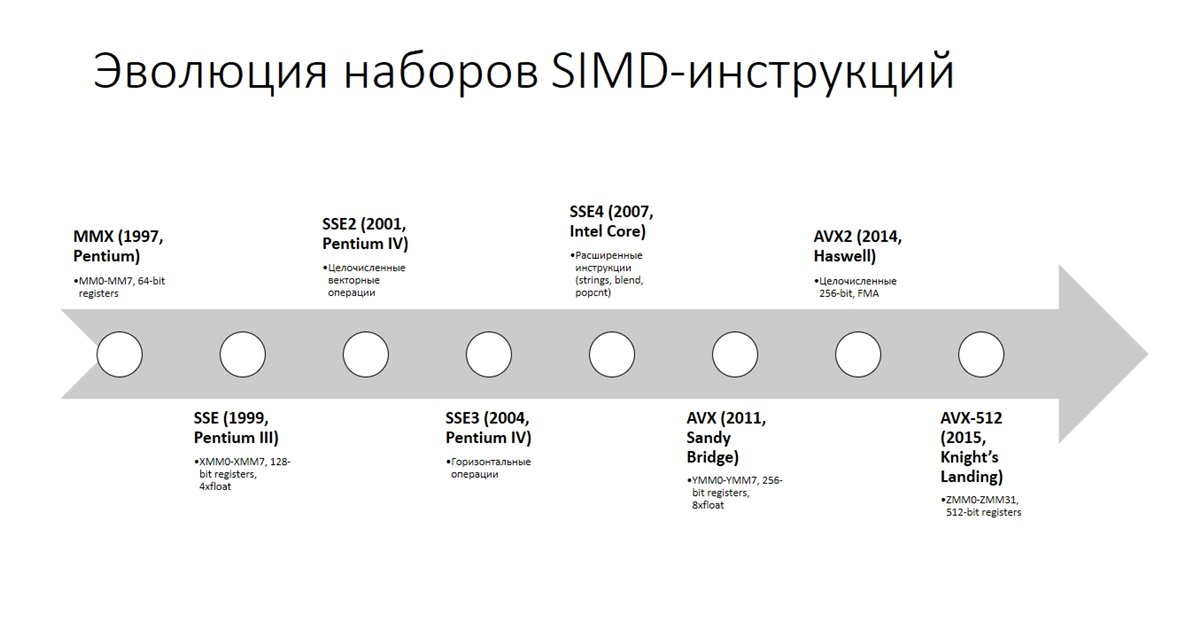
SSE (англ. Streaming SIMD Extensions, потоковое SIMD-расширение процессора) — это SIMD (англ. Single Instruction, Multiple Data, Одна инструкция — множество данных) набор инструкций. SSE включает в архитектуру процессора восемь 128-битных регистров и набор инструкций. Технология SSE была впервые введена в Pentium III в 1999 году. Со временем, этот набор инструкций был улучшен путем добавления более сложных операций. Восемь (в x86-64 — шестнадцать) 128-битовых регистров были добавлены к процессору: от xmm0 до xmm7.

Изначально эти регистры могли быть использованы только для одинарной точности вычислений (т.е. для типа float). Но после выхода SSE2, эти регистры могут использоваться для любого примитивного типа данных. Учитывая стандартную 32-разрядную машину таким образом, мы можем хранить и обрабатывать параллельно:
- 2 double
- 2 long
- 4 float
- 4 int
- 8 short
- 16 char
Если же использовать технологию AVX, то вы будете манипулировать уже 256-битными регистрами, соответственно больше чисел за одну инструкцию. Так уже есть и 512-битные регистры.
Сначала на примере С++ (кому не интересно, можете пропустить) мы напишем программу, которая будет суммировать два массива из 8 элементов типа float.
Пример векторизации на С++
Технология SSE в С++ реализована низкоуровневыми инструкциями, представленные в виде псевдокода, которые отражают команды на ассемблере. Так, например, команда __m128 _mm_add_ps(__m128 a, __m128 b ); преобразуется в инструкцию ассемблера ADDPS операнд1, операнд2. Соответственно команда __m128 _mm_add_ss(__m128 a, __m128 b ); будет преобразовываться в инструкцию ADDSS операнд1, операнд2. Эти две команды делают почти одинаковые операции: складывают элементы массива, но немного по-разному. _mm_add_ps складывает полностью регистр с регистром, так что:
- r0 := a0 + b0
- r1 := a1 + b1
- r2 := a2 + b2
- r3 := a3 + b3
При этом весь регистр __m128 и есть набор r0-r3. А вот команда _mm_add_ss складывает только часть регистра, так что:
- r0 := a0 + b0
- r1 := a1
- r2 := a2
- r3 := a3
По такому же принципу устроены и остальные команды, такие как вычитание, деление, квадратный корень, минимум, максимум и другие операции.
Для написания программы можно манипулировать 128-битовыми регистрами типа __m128 для float, __m128d для double и __m128i для int, short, char. При этом можно не использовать массивы типа __m128, а использовать приведенные указатели массива float к типу __m128*.
При этом следует учитывать несколько условий для работы:
- Данные float, загруженные и хранящиеся в __m128 объекте должны иметь 16-байтовое выравнивание
- Некоторые встроенные функции требуют, чтобы их аргумент был типа констант целых чисел, в силу природы инструкции
- Результат арифметических операций, действующих на два NAN аргументов, не определен
Такой вот маленький экскурс в теорию. Однако, рассмотрим пример программы с использованием SSE:
#include "iostream"
#include "xmmintrin.h"
int main()
{
const auto N = 8;
alignas(16) float a[] = { 41982.0, 81.5091, 3.14, 42.666, 54776.45, 342.4556, 6756.2344, 4563.789 };
alignas(16) float b[] = { 85989.111, 156.5091, 3.14, 42.666, 1006.45, 9999.4546, 0.2344, 7893.789 };
__m128* a_simd = reinterpret_cast<__m128*>(a);
__m128* b_simd = reinterpret_cast<__m128*>(b);
auto size = sizeof(float);
void *ptr = _aligned_malloc(N * size, 32);
float* c = reinterpret_cast<float*>(ptr);
for (size_t i = 0; i < N/2; i++, a_simd++, b_simd++, c += 4)
_mm_store_ps(c, _mm_add_ps(*a_simd, *b_simd));
c -= N;
std::cout.precision(10);
for (size_t i = 0; i < N; i++)
std::cout << c[i] << std::endl;
_aligned_free(ptr);
system("PAUSE");
return 0;
}
- alignas(#) — стандартный для С++ переносимый способ задания настраиваемого выравнивания переменных и пользовательских типов. Используется в С++11 и поддерживается Visual Studio 2015. Можно использовать и другой вариант — __declspec( align( #)) declarator. Данные средства для управления выравниванием при статическом выделении памяти. Если необходимо выравнивание с динамическим выделением, необходимо использовать void* _aligned_malloc(size_t size, size_t alignment);
- Затем преобразуем указатель на массив a и b к типу _m128* при помощи reinterpret_cast, который позволяет преобразовывать любой указатель в указатель любого другого типа.
- После динамически выделим выравненную память при помощи уже упомянутой выше функции _aligned_malloc(N*sizeof(float), 16);
- Количество необходимых байт выделяем исходя из количества элементов с учетом размерности типа, а 16 это значение выравнивания, которое должно быть степенью двойки. А затем указатель на этот участок памяти приводим к другому типу указателя, чтобы с ним можно было бы работать с учетом размерности типа float как с массивом.
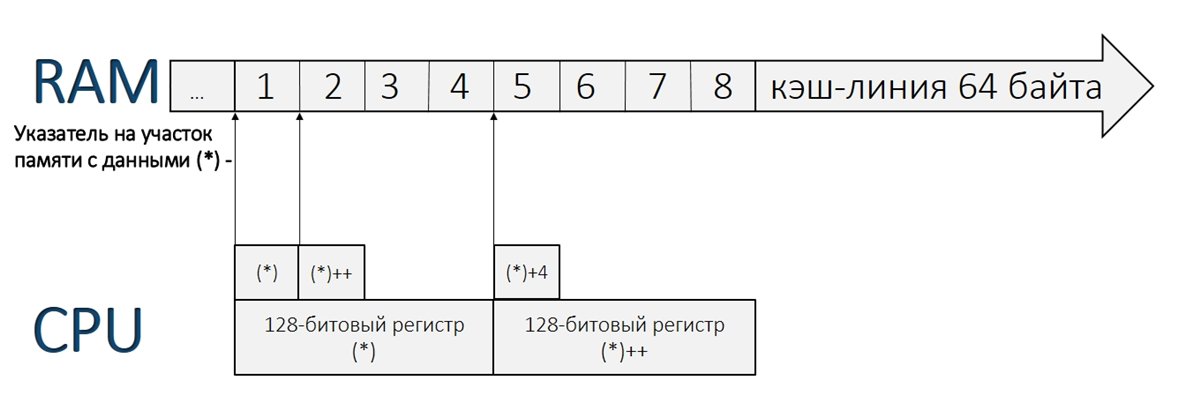
Таким образом все приготовления для работы SSE выполнены. Дальше в цикле суммируем элементы массивов. Подход основан на арифметике указателей. Так как a_simd, b_simd и с — это указатели, то их увеличение приводит к смещению на sizeof(T) по памяти. Если взять к примеру динамический массив с, то с[0] и *с покажут одинаковое значение, т.к. с указывает на первый элемент массива. Инкремент с приведет к смещению указателя на 4 байта вперед и теперь указатель будет указывать на 2 элемент массива. Таким образом можно двигаться по массиву вперед и назад увеличивая и уменьшая указатель. Но при этом следует учитывать размерность массива, так как легко выйти за его пределы и обратиться к чужому участку памяти. Работа с указателями a_simd и b_simd аналогична, только инкремент указателя приведет к перемещению на 128-бит вперед и при этом с точки зрения типа float будет пропущено 4 переменных массива a и b. В принципе указатель a_simd и a, как и b_simd и b указывают соответственно на один участок в памяти, за тем исключением, что обрабатываются они по-разному с учетом размерности типа указателя:
for (int i = 0; i < N/2; i++, a_simd++, b_simd++, c += 4)
_mm_store_ps(c, _mm_add_ps(*a_simd, *b_simd));
Теперь понятно почему в данном цикле такие изменения указателей. На каждой итерации цикла происходит сложение 4-х элементов и сохранение полученного результата по адресам указателя с из регистра xmm0 (для данной программы). Т.е. как мы видим такой подход не изменяет исходных данных, а хранит сумму в регистре и по необходимости передает ее в нужный нам операнд. Это позволяет повысить производительность программы в тех случаях, когда необходимо повторно использовать операнды.
Рассмотрим код, который генерирует ассемблер для метода _mm_add_ps:
mov eax,dword ptr [b_simd] ;// поместить адрес b_simd в регистр eax(базовая команда пересылки данных, источник не изменяется)
mov ecx,dword ptr [a_simd] ;// поместить адрес a_simd в регистр ecx
movups xmm0,xmmword ptr [ecx] ;// поместить 4 переменные с плавающей точкой по адресу ecx в регистр xmm0; xmm0 = {a[i], a[i+1], a[i+2], a[i+3]}
addps xmm0,xmmword ptr [eax] ;// сложить переменные: xmm0 = xmm0 + b_simd
;// xmm0[0] = xmm[0] + b_simd[0]
;// xmm0[1] = xmm[1] + b_simd[1]
;// xmm0[2] = xmm[2] + b_simd[2]
;// xmm0[3] = xmm[3] + b_simd[3]
movaps xmmword ptr [ebp-190h],xmm0 ;// поместить значение регистра по адресу в стеке со смещением
movaps xmm0,xmmword ptr [ebp-190h] ;// поместить в регистр
mov edx,dword ptr [c] ;// поместить в регистр ecx адрес переменной с
movaps xmmword ptr [edx],xmm0 ;// поместить значение регистра в регистр ecx или сохранить сумму по адресу памяти, куда указывает (ecx) или с. При этом xmmword представляет собой один и тот же тип, что и _m128 - 128-битовое слово, в котором 4 переменные с плавающей точкой
Как видно из кода, одна инструкция addps обрабатывает сразу 4 переменных, которая реализована и поддерживается аппаратно процессором. Система не принимает никакого участия при обработке этих переменных, что дает хороший прирост производительности без лишних затрат со стороны.
При этом хотел бы отметить одну особенность, что в данном примере и компилятором используется инструкция movups, для которой не требуются операнды, которые должны быть выровнены по 16-байтовой границе. Из чего следует, что можно было бы не выравнивать массив a. Однако, массив b необходимо выровнять, иначе в операции addps возникнет ошибка чтения памяти, ведь регистр складывается со 128-битным расположением в памяти. В другом компиляторе или среде могут быть другие инструкции, поэтому лучше в любом случае для всех операндов, принимающих участие в подобных операциях, делать выравнивание по границе. Во всяком случае во избежание проблем с памятью.
Еще одна причина делать выравнивание, так это когда мы оперируем с элементами массивов (и не только с ними), то на самом деле постоянно работаем с кэш-линиями размером по 64 байта. SSE и AVX векторы всегда попадают в одну кэш линию, если они выравнены по 16 и 32 байта, соответственно. А вот если наши данные не выравнены, то, очень вероятно, нам придётся подгружать ещё одну «дополнительную» кэш-линию. Процесс этот достаточно сильно сказывается на производительности, а если мы при этом и к элементам массива, а значит, и к памяти, обращаемся непоследовательно, то всё может быть ещё хуже.
Поддержка SIMD в .NET
Впервые упоминание o поддержке JIT технологии SIMD было объявлено в блоге .NET в апреле 2014 года. Тогда разработчики анонсировали новую превью-версию RyuJIT, которая обеспечивала SIMD функциональность. Причиной добавления стала довольно высокая популярность запроса на поддержку C# and SIMD. Изначальный набор поддерживаемых типов был не большим и были ограничения по функциональности. Изначально поддерживался набор SSE, а AVX обещали добавить в релизе. Позже были выпущены обновления и добавлены новые типы с поддержкой SIMD и новые методы для работы с ними, что в последних версиях представляет обширную и удобную библиотеку для аппаратной обработки данных.
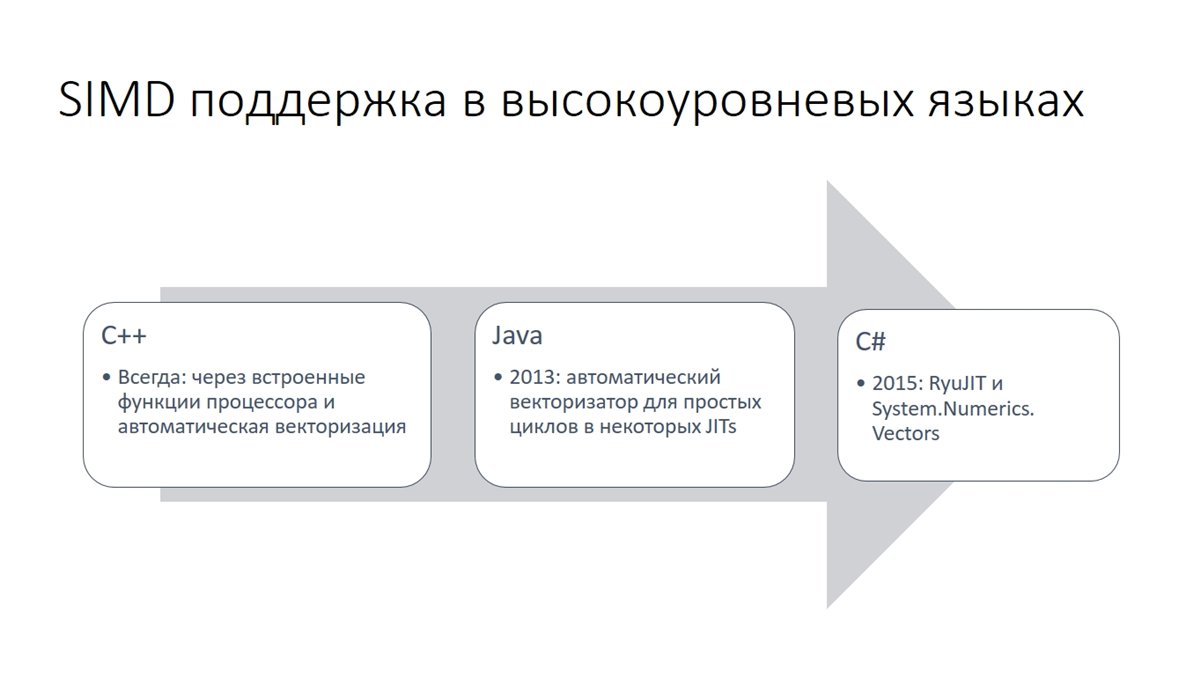
Такой подход облегчает жизнь разработчика, который не должен писать CPU-зависимый код. Вместо этого CLR абстрагирует аппаратное обеспечение, предоставляя виртуальную исполняющую среду, которая переводит свой код в машинные команды либо во время выполнения (JIT), либо во время установки (NGEN). Оставляя генерацию кода CLR, вы можете использовать один и тот же MSIL код на разных компьютерах с разными процессорами, не отказываясь от оптимизаций, специфических для данного конкретного CPU.
На данный момент поддержка этой технологии в .NET представлена в пространстве имен System.Numerics.Vectors и представляет собой библиотеку векторных типов, которые могут использовать преимущества аппаратного ускорения SIMD. Аппаратное ускорение может приводить к значительному повышению производительности при математическом и научном программировании, а также при программировании графики. Она содержит следующие типы:
- Vector — коллекцию статических удобных методов для работы с универсальными векторами
- Matrix3x2 — представляет матрицу 3х2
- Matrix4х4 — представляет матрицу 4х4
- Plane — представляет трехмерную плоскость
- Quaternion — представляет вектор, используемый для кодирования трехмерных физических поворотов
- Vector<(Of <(<'T>)>)> представляет вектор указанного числового типа, который подходит для низкоуровневой оптимизации параллельных алгоритмов
- Vector2 — представляет вектор с двумя значениями одинарной точности с плавающей запятой
- Vector3 — представляет вектор с тремя значениями одинарной точности с плавающей запятой
- Vector4 — представляет вектор с четырьмя значениями одинарной точности с плавающей запятой
Класс Vector предоставляет методы для сложения, сравнения, поиска минимума и максимума и многих других преобразований над векторами. При этом операции работают с использованием технологии SIMD. Остальные типы также поддерживают аппаратное ускорение и содержат специфические для них преобразования. Для матриц это может быть перемножение, для векторов евклидово расстояние между точками и т.д.
Пример программы на C#
Итак, что необходимо для того, чтобы использовать данную технологию? Необходимо в первую очередь иметь RyuJIT компилятор и версию .NET 4.6. System.Numerics.Vectors через NuGet не ставится, если версия ниже. Однако, уже при установленной библиотеке я понижал версию и все работало как надо. Затем необходима сборка под x64, для этого необходимо убрать в свойствах проекта «предпочитать 32-разрядную платформу» и можно собирать под Any CPU.
Листинг:
using System;
using System.Numerics;
class Program
{
static void Main(string[] args)
{
const Int32 N = 8;
Single[] a = { 41982.0F, 81.5091F, 3.14F, 42.666F, 54776.45F, 342.4556F, 6756.2344F, 4563.789F };
Single[] b = { 85989.111F, 156.5091F, 3.14F, 42.666F, 1006.45F, 9999.4546F, 0.2344F, 7893.789F };
Single[] c = new Single[N];
for (int i = 0; i < N; i += Vector<Single>.Count) // Count возвращает 16 для char, 4 для float, 2 для double и т.п.
{
var aSimd = new Vector<Single>(a, i); // создать экземпляр со смещением i
var bSimd = new Vector<Single>(b, i);
Vector<Single> cSimd = aSimd + bSimd; // или так Vector<Single> c_simd = Vector.Add(b_simd, a_simd);
cSimd.CopyTo(c, i); //копировать в массив со смещением
}
for (int i = 0; i < a.Length; i++)
{
Console.WriteLine(c[i]);
}
Console.ReadKey();
}
}
С общей точки зрения что С++ подход, что .NET довольно схожи. Необходимо преобразование/копирование исходных данных, выполнить копирование в конечный массив. Однако, подход с C# намного проще, многие вещи сделаны за Вас и Вам только остается пользоваться и наслаждаться. Нет необходимости думать о выравнивании данных, заниматься выделением памяти и делать это статически, либо динамически с определенными операторами. С другой стороны у вас больший контроль над происходящим с использованием указателей, но и больше ответственности за происходящее.
А в цикле происходит все так, как и в цикле в С++. И я не про указатели. Алгоритм расчета такой же. На первой итерации мы заносим первые 4 элемента исходных массивов в структуру aSimd и bSimd, затем суммируем и сохраняем в конечном массиве. Затем на следующей итерации заносим следующие 4 элемента при помощи смещения и суммируем их. Вот так все просто и быстро делается. Рассмотрим код, который генерирует компилятор для этой команды var cSimd = aSimd + bSimd:
addps xmm0,xmm1
Отличие от С++ версии только в том, что тут складываются оба регистра, в то время как там было складывание регистра с участком памяти. Помещение в регистры происходит при инициализации aSimd и bSimd. В целом данный подход, если сравнивать код компиляторов С++ и .NET не особо отличается и дает приблизительно равную производительность. Хотя вариант с указателями будет работать все равно быстрее. Хотелось бы отметить, что SIMD-инструкции генерируются при включенной оптимизации кода. Т.е. увидеть их в дизассемблере в Debug не получится: это реализовано в виде вызова функции. Однако в Release, где включена оптимизация, вы получите эти инструкции в явном(встроенном) виде.
Напоследок
Что мы имеем:
- Во многих случаях векторизация дает 4-8× увеличение производительности
- Сложные алгоритмы потребуют изобретательность, но без этого никуда
- System.Numerics.Vectors в настоящее время обхватывает только часть simd-инструкций. Для более серьезного подхода потребуется С++
- Есть множество других способов помимо векторизации: правильное использование кэша, многопоточность, гетерогенные вычисления, грамотная работа с памятью(чтобы сборщик мусора не потел) и т.д.
В ходе краткой твиттер-переписки с Сашой Голдштейном(одного из авторов книги «Оптимизация приложений на платформе .NET»), который рассматривал аппаратное ускорение в .NET, я поинтересовался, что как на его взгляд реализована поддержка SIMD в .NET и какова она в сравнении с С++. На что он ответил: «Несомненно, вы можете сделать больше на С++, чем на C#. Но вы действительно получаете кросс-процессорную поддержку на С#. Например, автоматический выбор между SSE4 и AVX». В целом, это не может не радовать. Ценой малых усилий мы можем получать от системы как можно большей производительности, задействуя все возможные аппаратные ресурсы.
Для меня это очень хорошая возможность разрабатывать производительные программы. По крайней мере у себя в дипломной работе, по моделированию физических процессов, я в основном добивался эффективности путем создания некоторого количества потоков, а также при помощи гетерогенных вычислений. Использую как CUDA, так и C++ AMP. Разработка ведется на универсальной платформе под Windows 10, где меня очень привлекает WinRT, который позволяет писать программу как на C#, так и на С++/CX. В основном на плюсах пишу ядро для больших расчетов (Boost), а на C# уже манипулирую данными и разрабатываю интерфейс. Естественно, перегон данных через двоичный интерфейс ABI для взаимодействия двух языков имеет свою цену(хотя и не очень большую), что требует более разумной разработки библиотеки на С++. Однако у меня данные пересылаются только в случае необходимости и довольно редко, только для отображения результатов.
В случае надобности манипулирования данными в C#, я их преобразую в типы .NET, чтобы не работать с типами WinRT, тем самым увеличивая производительность обработки уже на C#. Так например, когда нужно обработать несколько тысяч или десятков тысяч элементов или требования к обработке не имеют никаких особых спецификаций, данные можно рассчитать в C# без задействования библиотеки (в ней считаются от 3 до 10 миллионов экземпляров структур, иногда только за одну итерацию). Так что подход с аппаратным ускорением упростит задачу и сделает ее быстрее.

Список источников при написании статьи
- Перевод статьи блога .NET про новый JIT с поддержкой SIMD
- Про System.Numerics.Vector в блоге .NET
- Что такое выравнивание, и как оно влияет на работу ваших программ
- Блог компании Intel про выравнивании данных при векторизации циклов
Ну и отдельное спасибо Саше Голдштейну за предоставленную помощь и информацию.
Автор: Priest512






