Визуализация пересечений и перекрытий с помощью Python

Изучение вариантов решения одной из самых сложных задач визуализации данных

Преобладающая задача в любом анализе данных — сравнение нескольких наборов чего-либо. Это могут быть списки IP-адресов для каждой целевой страницы вашего сайта, клиенты, которые купили определённые товары в вашем магазине, несколько ответов из опроса и многое другое.

В этой статье воспользуемся Python для изучения способов визуализации перекрытий и пересечений множеств, наших возможностей, а также их преимуществ и недостатков.

Диаграмма Венна

---

В следующих примерах я воспользуюсь датасетом из переписи общества визуализации данных 2020 года.

Я буду работать с опросом, потому что в нём много разнотипных вопросов; некоторые из них — это вопросы со множественным выбором и несколькими ответами, как показано ниже.

Источник — Datavisualizationsurvey Git

Допустим, мы будем считать каждый ответ. В нашей диаграмме итоговые числа будут больше, чем общее число респондентов, что может вызвать трудности в понимания аудиторией, будут подниматься вопросы, непонимание заставит аудиторию скептически относиться к данным.

Например, если бы у нас было 100 респондентов и три возможных ответа — A, B и C.

У нас может быть что-то вроде этого:
50 ответов — A и B;
25 ответов — А и С;
25 ответов — А.

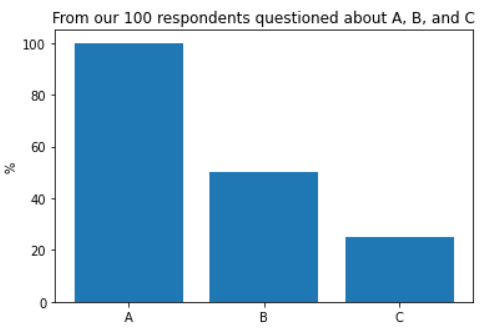
Гистограмма

Выглядит запутанным. Даже если мы объясним аудитории, что респондент может выбрать несколько вариантов ответа, трудно понять, что представляет собой эта диаграмма.

Кроме того, с такой визуализацией у нас нет никакой информации о пересечении ответов. Например, нельзя сказать, что никто не выбрал все три варианта.

Диаграммы Венна

Давайте начнём с простого и очень знакомого решения — диаграмм Венна. Я использую Matplotlib-Venn для этой задачи.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from matplotlib_venn import venn3, venn3_circles
from matplotlib_venn import venn2, venn2_circles

Теперь загрузим набор данных и подготовим данные, которые хотим проанализировать.

Вопрос, который мы проверим: «Что из этого лучше всего описывает вашу роль в качестве визуализатора данных за прошедший год?»

Ответы на этот вопрос распределены по 6 столбцам, по одному на каждый ответ. Если респондент выбрал ответ, в поле появится текст. Если нет, поле будет пустым. Мы преобразуем эти данные в 6 списков, содержащих индексы выбравших каждый ответ пользователей.

df = pd.read_csv('data/2020/DataVizCensus2020-AnonymizedResponses.csv')
nm = 'Which of these best describes your role as a data visualizer in the past year?'
d1 = df[~df[nm].isnull()].index.tolist() # independent
d2 = df[~df[nm+'_1'].isnull()].index.tolist() # organization
d3 = df[~df[nm+'_2'].isnull()].index.tolist() # hobby
d4 = df[~df[nm+'_3'].isnull()].index.tolist() # student
d5 = df[~df[nm+'_4'].isnull()].index.tolist() # teacher
d6 = df[~df[nm+'_5'].isnull()].index.tolist() # passive income

Диаграммы Венна просты в понимании и применении.

Нам нужно передать наборы с ключами/предложениями, которые мы будем анализировать. Если это пересечение двух наборов, воспользуемся Venn2; если это три набора, тогда используем Venn3.

venn2([set(d1), set(d2)])
plt.show()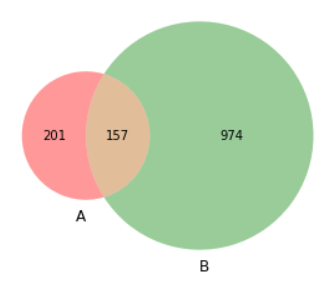

Диаграмма Венна

Здорово! С помощью диаграмм Венна мы можем чётко показать, что 201 респондент выбрал А и не выбрал B, 974 респондента выбрали B и не выбрали A, а 157 респондентов выбрали A и B.

Можно даже настроить некоторые аспекты графика.

venn2([set(d1), set(d2)], 
      set_colors=('#3E64AF', '#3EAF5D'), 
      set_labels = ('FreelancenConsultantn
Independent contractor', 
                    'Position in an organizationnwith some data
viz job responsibilities'),
      alpha=0.75)
venn2_circles([set(d1), set(d2)], lw=0.7)
plt.show()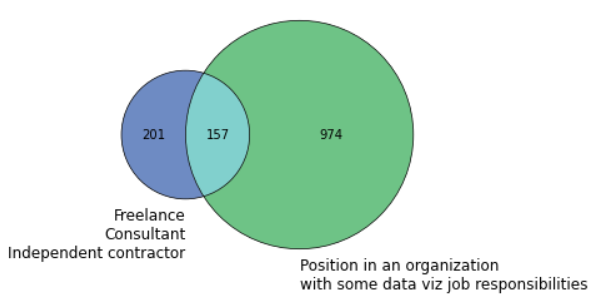

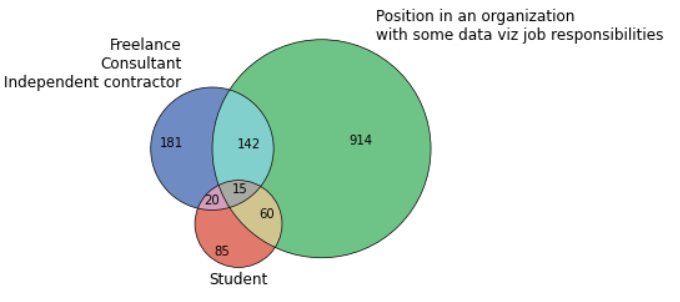
venn3([set(d1), set(d2), set(d5)],
      set_colors=('#3E64AF', '#3EAF5D', '#D74E3B'), 
      set_labels = ('FreelancenConsultantn
Independent contractor', 
                    'Position in an organizationnwith some data 
viz job responsibilities',
                    'AcademicnTeacher'),
      alpha=0.75)
venn3_circles([set(d1), set(d2), set(d5)], lw=0.7)
 
plt.show()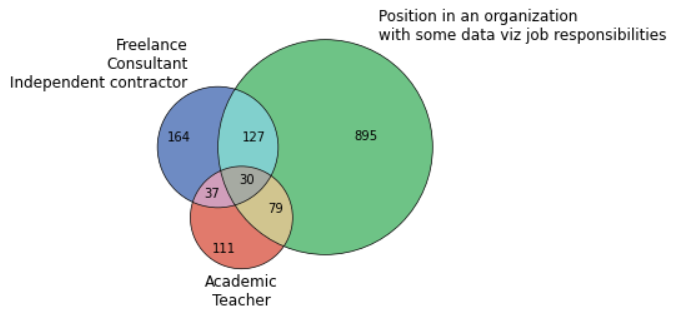

Это здорово, но что, если мы захотим отобразить перекрытия более трёх наборов? Здесь есть пара возможностей. Например, мы могли бы использовать несколько диаграмм.

labels = ['FreelancenConsultantnIndependent contractor',
          'Position in an organizationnwith some data viznjob responsibilities', 
          'Non-compensatedndata visualization hobbyist',
          'Student',
          'Academic/Teacher',
          'Passive income fromndata visualizationnrelated products']
c = ('#3E64AF', '#3EAF5D')
# subplot indexes
txt_indexes = [1, 7, 13, 19, 25]
title_indexes = [2, 9, 16, 23, 30]
plot_indexes = [8, 14, 20, 26, 15, 21, 27, 22, 28, 29]
# combinations of sets
title_sets = [[set(d1), set(d2)], [set(d2), set(d3)], 
              [set(d3), set(d4)], [set(d4), set(d5)], 
              [set(d5), set(d6)]]
plot_sets = [[set(d1), set(d3)], [set(d1), set(d4)], 
             [set(d1), set(d5)], [set(d1), set(d6)],
             [set(d2), set(d4)], [set(d2), set(d5)],
             [set(d2), set(d6)], [set(d3), set(d5)],
             [set(d3), set(d6)], [set(d4), set(d6)]]
fig, ax = plt.subplots(1, figsize=(16,16))
# plot texts
for idx, txt_idx in enumerate(txt_indexes):
    plt.subplot(6, 6, txt_idx)
    plt.text(0.5,0.5,
             labels[idx+1], 
             ha='center', va='center', color='#1F764B')
    plt.axis('off')
# plot top plots (the ones with a title)
for idx, title_idx in enumerate(title_indexes):
    plt.subplot(6, 6, title_idx)
    venn2(title_sets[idx], set_colors=c, set_labels = (' ', ' '))
    plt.title(labels[idx], fontsize=10, color='#1F4576')
# plot the rest of the diagrams
for idx, plot_idx in enumerate(plot_indexes):
    plt.subplot(6, 6, plot_idx)
    venn2(plot_sets[idx], set_colors=c, set_labels = (' ', ' '))
plt.savefig('venn_matrix.png')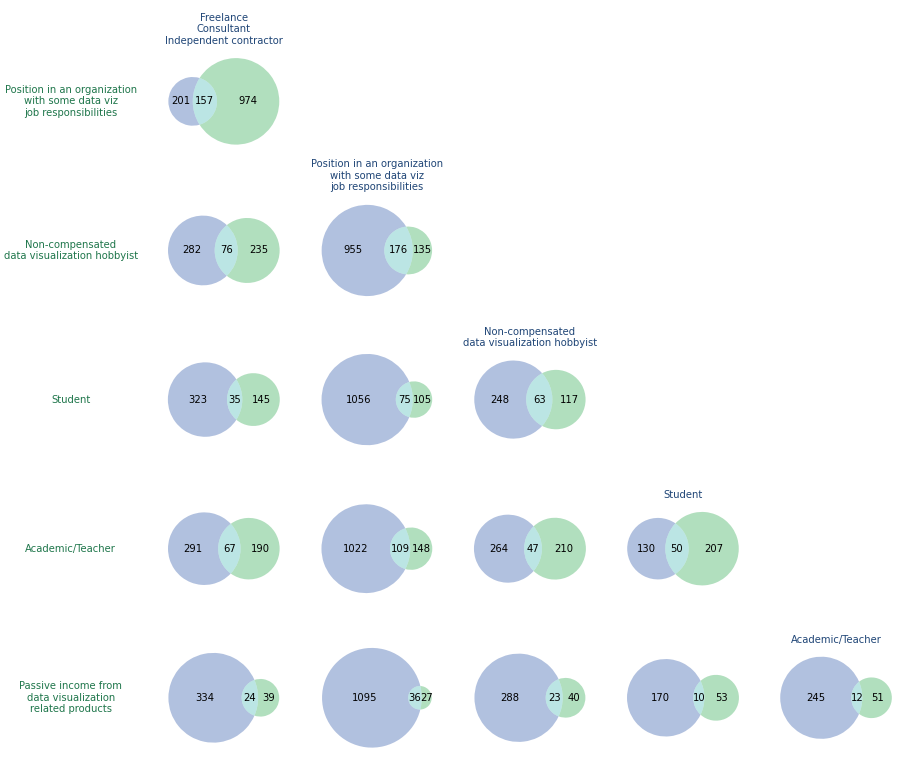

Матрица диаграммы Венна

Ничего страшного, но это не решило проблему. Мы не можем определить, есть ли кто-то, кто выбрал все ответы, а также невозможно определить пересечение трёх наборов. Как насчёт диаграммы Венна с четырьмя кругами?

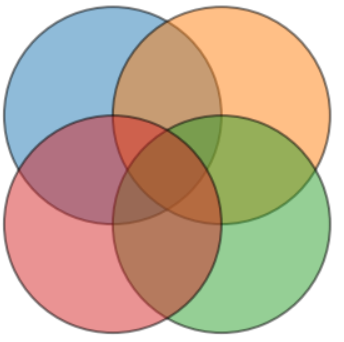
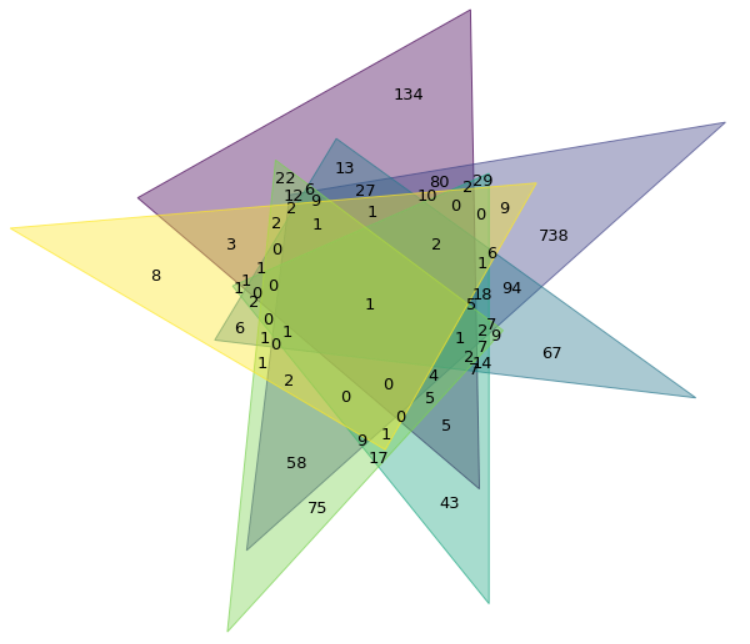
Здесь всё начинает усложняться. На изображении выше нет пересечения только синего и зелёного. Чтобы решить эту проблему, вместо кругов мы можем использовать эллипсы.

В двух следующих примерах применяется PyVenn.

from venn import venn
sets = {
    labels[0]: set(d1),
    labels[1]: set(d2),
    labels[2]: set(d3),
    labels[3]: set(d4)
}
fig, ax = plt.subplots(1, figsize=(16,12))
venn(sets, ax=ax)
plt.legend(labels[:-2], ncol=6)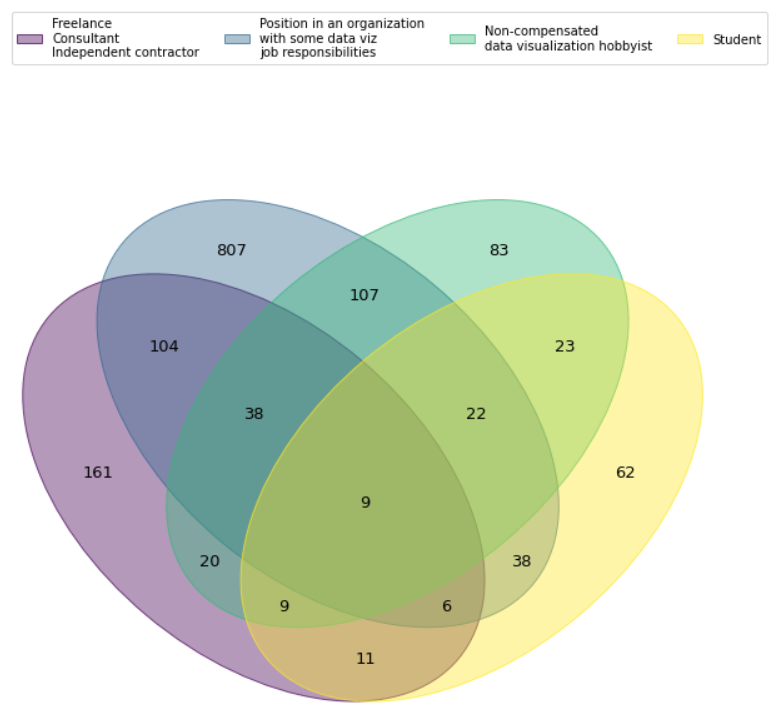

Вот оно!

Но мы потеряли размер — критически важную для диаграммы информацию. Синий (807) меньше жёлтого (62), что не очень помогает в визуализации. Чтобы понять, что есть что, мы можем использовать легенду и метки, но таблица была бы яснее.

Есть несколько реализаций пространственных пропорциональных диаграмм Венна, которые могут работать с более чем тремя наборами, но на Python я не смог найти ни одной.

График UpSet

Но есть и другое решение. Графики UpSet — отличный способ отображения пересечения нескольких множеств. Они не так интуитивно понятны для чтения, как диаграммы Венна, но делают свою работу. Я воспользуюсь UpSetPlot, но сначала подготовлю данные.

upset_df = pd.DataFrame()
col_names = ['Independent', 'Work for Org', 'Hobby', 'Student', 'Academic', 'Passive Income']
nm = 'Which of these best describes your role as a data visualizer in the past year?'
for idx, col in enumerate(df[[nm, nm+'_1', nm+'_2', nm+'_3', nm+'_4', nm+'_5']]):
    temp = []
    for i in df[col]:
        if str(i) != 'nan':
            temp.append(True)
        else:
            temp.append(False)
    upset_df[col_names[idx]] = temp
    
upset_df['c'] = 1
example = upset_df.groupby(col_names).count().sort_values('c')
example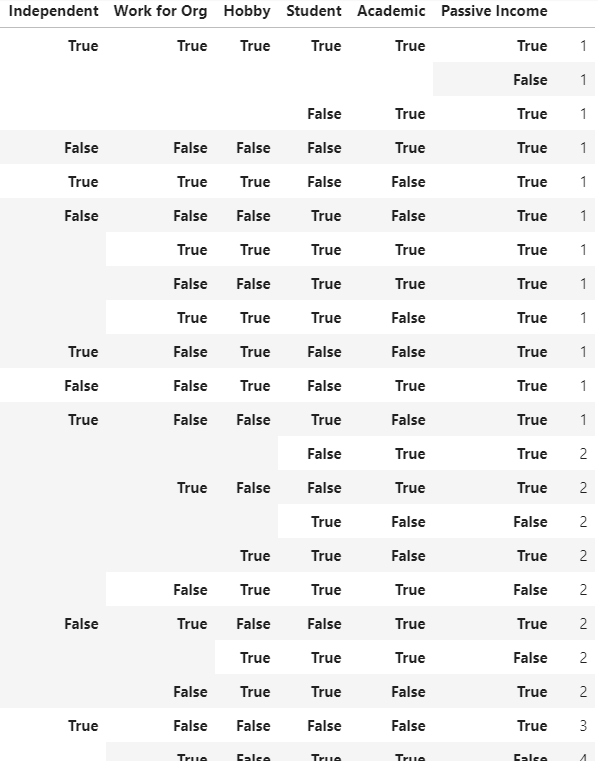

При правильном расположении данных нам нужен только один метод, чтобы нарисовать нашу диаграмму, и всё.

upsetplot.plot(example['c'], sort_by="cardinality")
plt.title('Which of these best describes your role as a data visualizer in the past year?', loc='left')
plt.show()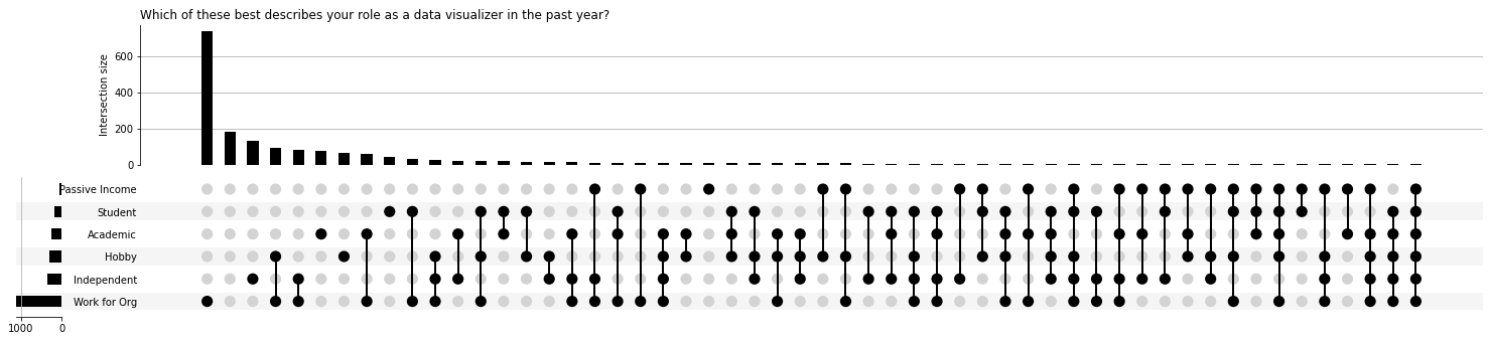

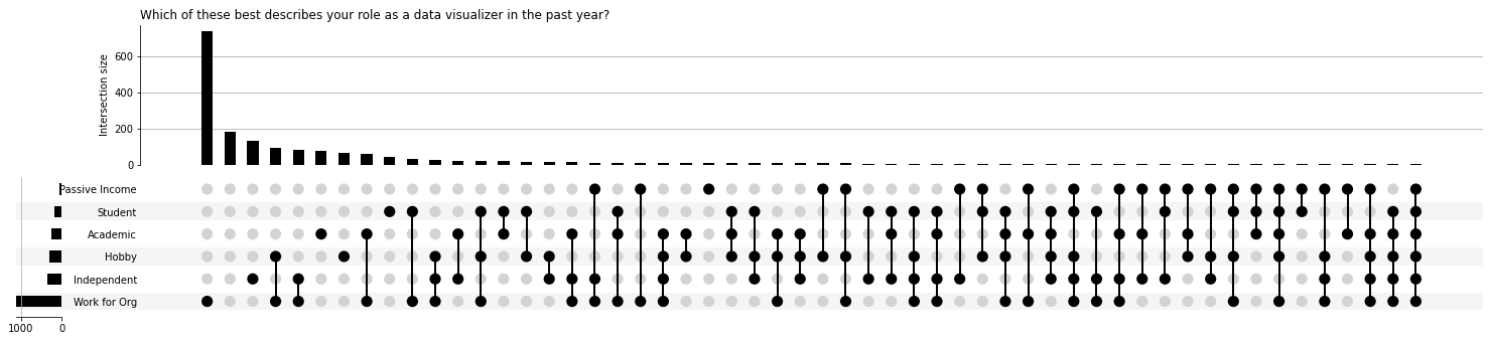
График UpSet

Потрясающе! Наверху — столбцы, показывающие, сколько раз появлялась комбинация. Внизу — матрица, показывающая, какую комбинацию представляет каждый столбец, а внизу слева — горизонтальная гистограмма, представляющая общий размер каждого набора.

Это большое количество информации, но хорошо организованный макет позволяет легко извлекать её.

Даже с моими плохо написанными метками мы легко можем увидеть, что большинство людей выбрали «работать на организацию».

Второй наиболее распространённый ответ даже не отображался на предыдущих диаграммах Венна: количество людей, которые не выбрали ни одного ответа.

В целом визуализация множеств и их пересечений может быть задачей для решения в уме, но у нас есть несколько хороших вариантов её решения.

Я предпочитаю диаграммы Венна, когда имею дело с небольшим количеством множеств, и графики Upset, когда множеств больше трёх. Всегда полезно объяснить, что показывает визуализация и как читать диаграммы, которые вы представляете, особенно в случаях, когда диаграммы не очень дружелюбны.

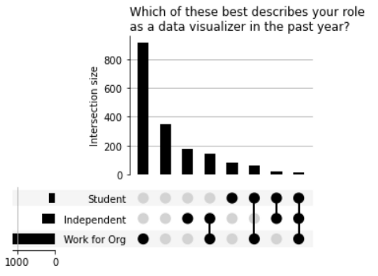
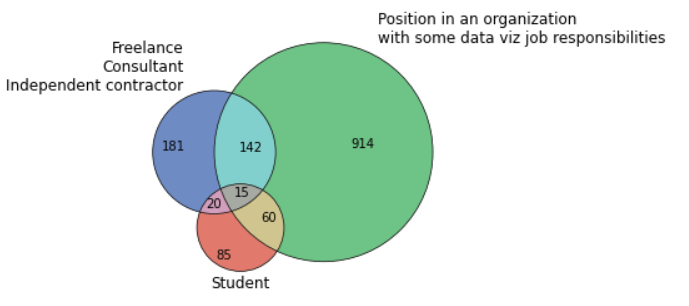
Визуализация трех наборов

Визуализация шести наборов

• Обучение профессии Data Science
• Обучение профессии Data Analyst

Автор: one-two

Источник