ABBYY Cup: разбор полётов

Умный Бобер из ABBYY уже давно сотрудничает с НИИ «Цитологии и Генетики». Недавно работники этого НИИ предложили Бобру новую задачу. Суть задачи заключалась в следующем.

Есть набор из n белков (не обязательно различных). Каждый белок представляет собой строку, состоящую из маленьких букв латинского алфавита. Задача, которую поставили перед Умным Бобром ученые, заключается в выборе поднабора мощности k из исходного набора белков, причём репрезентативность выбранного поднабора белков должна быть максимальной.

Умный Бобер из ABBYY провел небольшое исследование и пришел к выводу, что репрезентативность набора белков можно оценить одним числом, которое достаточно просто вычисляется. Пусть у нас есть набор {a₁, ..., a_k} из k строк, описывающих белки. Репрезентативностью этого набора называется следующая величина: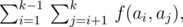
где f(x, y) — длина наибольшего общего префикса строк x и y; например, f(«abc», «abd») = 2, а f(«ab», «bcd») = 0. Таким образом, репрезентативность набора белков {«abc», «abd», «abe»} равна 6, а набора {«aaa», «ba», «ba»} — 2.

После этого открытия Умный Бобер из ABBYY обратился к участникам Cup'а с просьбой написать программу, выбирающую из заданного набора белков поднабор мощности k, который имеет наибольшее возможное значение репрезентативности. Помогите ему с решением этой задачи!

Сразу приступим к полному решению задачи. Давайте отсортируем строки лексикографически и посчитаем lcp[i] – длину наибольшего общего префикса строк i и i + 1. Несложно доказать, что наибольший общий префикс любых двух строк i и j теперь равен min (lcp[i], lcp[i + 1], …, lcp[j - 1]) (подобное утверждение используется при использовании суффиксного массива). Это полезно.

Теперь применим метод динамического программирования. Сделаем такое ДП: F(i, j, k) — максимальный возможный ответ на задачу, если из строк с номерами i… j нужно выбрать ровно k строк. Переход следующий: найдём позицию p на отрезке i… j - 1 с минимальным lcp[p], тогда F(i, j, k) = max_{q = 0… k}(F(i, p, q) + F(p + 1, j, k - q) + q· (k - q)· lcp[p]), то есть предполагаем, что выбрано q из строк из i… p, k - q строк из p + 1… j, и для всех пар этих строк длина наибольшего общего префикса равна lcp[p] (это следует из утверждения в первом абзаце).

Такое решение достаточно для получения 50 баллов. Пока что кажется, что сложность этого решения порядка O(N⁴). Осталось показать, что на самом деле можно реализовать это решение так, чтобы его сложность оказалась равна O(N²).Для начала заметим, что различных отрезков i… j, на которых нас интересуют значения функции F, на самом деле ровно 2N - 1, а не O(N²). Почему это так, можно понять из переходов нашего ДП. Отрезок 1… N разбивается на два отрезка 1… p и p + 1… N, каждый из этих отрезков разбивается ещё на два отрезка, и так далее; видим, что между позициями i и i + 1 для любого i ровно один раз за весь подсчёт ДП произойдёт «разрез», и этот разрез породит два новых отрезка, на которых нас интересуют значения ДП. Отсюда и получаем оценку в 2N - 1 нужных отрезков, следовательно, наше решение уже имеет сложность не более O(N³).

Последнее и самое сложное — догадаться, что решение выше может иметь сложность O(N²). Например, реализовать его можно так. Давайте заведём рекурсивную функцию F(i, j), возвращающую массив длины j - i + 2 — собственно значения ДП F(i, j, k) (понятно, что нас интересуют только значения k из отрезка от 0 до j - i + 1). Внутри этой функции делаем следующее: найдём p, вызовем F(i, p) и F(p + 1, j), теперь переберём x от 0 до p - i + 1, переберём y от 0 до j - p и обновим значение F(i, j, x + y), если оно улучшилось (подробнее можно увидеть в авторском решении, там всё довольно прозрачно). Максимальное время работы функции F, вызванной на отрезке i… j длины j - i + 1 = N, можно записать как T(N) = max_{X = 1..N - 1}(T(X) + T(N - X) + (X + 1)·(N - X + 1)). Осталось понять, что T(N) = O(N²). Это можно сделать, например, написав простое ДП для подсчёта T. Если подумать, то можно понять это так: когда мы в цикле перебираем x = 0… p - i + 1 и y = 0… j - p, давайте будем представлять, что мы перебираем как будто пару строк: x = i… p и y = p + 1… j (тут перебор по x и y проходит на одну итерацию меньше, но это не принципиально); тогда каждая пара строк за весь подсчёт ДП окажется перебрана ровно один раз, что и даёт нам итоговую сложность O(N²).

Вот здесь можно ознакомиться с авторским решением.

Многие участники сдавали решения, использующее бор. Такие решения также могут иметь сложность O(N²), однако работают дольше и используют намного больше памяти. Тем не менее, ограничения по времени и по памяти были достаточно лояльны к разным решениям :)