Всё-таки я не зря учился! Как клёвые алгоритмы и школьные формулы помогают создавать инновационные лекарства

Введение

Меня зовут Александр Садовников, я выпускник корпоративной магистерской программы ИТМО и JetBrains «Разработка программного обеспечения» и по совместительству старший разработчик биоинформатического ПО в департаменте вычислительной биологии компании BIOCAD.

В этом посте я в доступной форме и без чрезмерного жонглирования нудными биоинформатическими терминами опишу один из ключевых этапов создания лекарственного средства — этап предсказания места взаимодействия лекарства с целевой молекулой в организме человека. Данная тема выбрана мной не случайно: в рамках своей дипломной работы я занимался именно этой проблемой.

Понять, как взаимодействуют две молекулы, можно, если предсказать структуру комплекса, который они формируют в природе. Предсказание структуры молекулярного комплекса по-научному называется задачей докинга. Частого использования этого термина я, к сожалению, избежать не смогу. Главная новость заключается в том, что задачу докинга человечество уже умеет с переменным успехом решать с помощью компьютерного моделирования. Это стало возможным, в частности, за счёт использования довольно известных за пределами биоинформатики алгоритмов и математических подходов. На их примере я покажу, как очень частные знания, которые мы получаем на протяжении многих лет учёбы в школе и вузе, оказываются полезными на практике, причём зачастую не самым очевидным образом.

Хочется верить, что данный материал будет интересен и полезен любому читателю, однако, чтобы понять всю техническую сторону вопроса, потребуются некоторые знания в области математики и алгоритмов.

Зачем нужно предсказывать структуру молекулярного комплекса

В современной фармацевтической промышленности всё большую популярность набирают лекарственные средства, основанные на взаимодействии антител с другими молекулами. Вообще антитела представляют собой молекулы иммунной системы, но люди научились создавать их и в лабораторных условиях, причём созданные искусственным образом антитела могут выполнять абсолютно разные терапевтические функции. Например, мы можем создать антитело, которое свяжется с раковой клеткой и привлечёт другие молекулы иммунной системы для её уничтожения. Или мы можем создать антитело, которое соединит друг с другом два белка, отсутствие взаимодействия между которыми вызывает несвёртываемость крови у больных гемофилией. В общем, антителам можно найти массу применений!

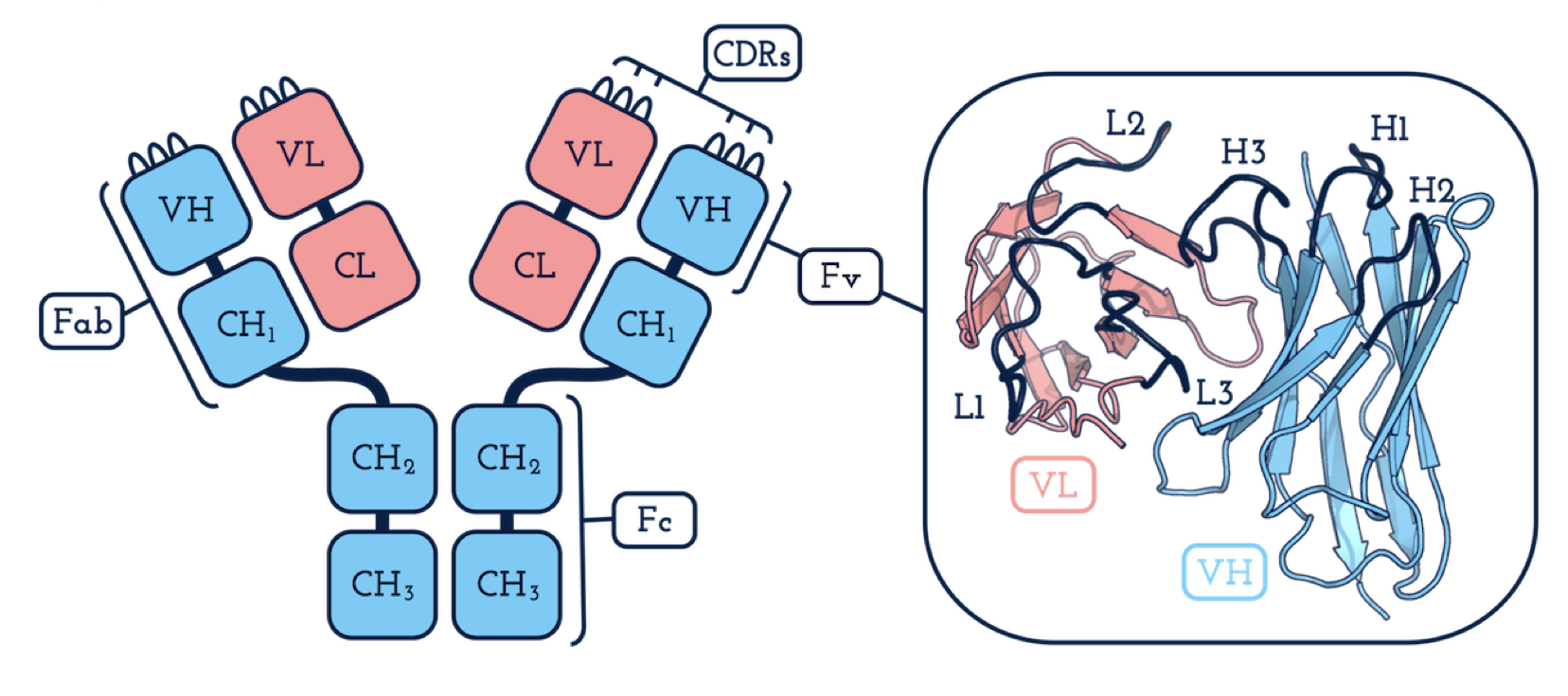
Структура антитела

Антитело состоит из нескольких частей. Наиболее значимыми частями в контексте способности антитела взаимодействовать с другими молекулами являются его петли (на рисунке петли помечены как L1, L2, L3 и H1, H2, H3). Название этих частей антитела обусловлено их формой: посмотрите на рисунок — действительно же петли какие-то! От структуры петель антитела зависит сила его связывания с поверхностью целевой молекулы и геометрические свойства данного взаимодействия. Поэтому при разработке лекарственных средств на основе антител наибольшее внимание уделяется именно петлям.

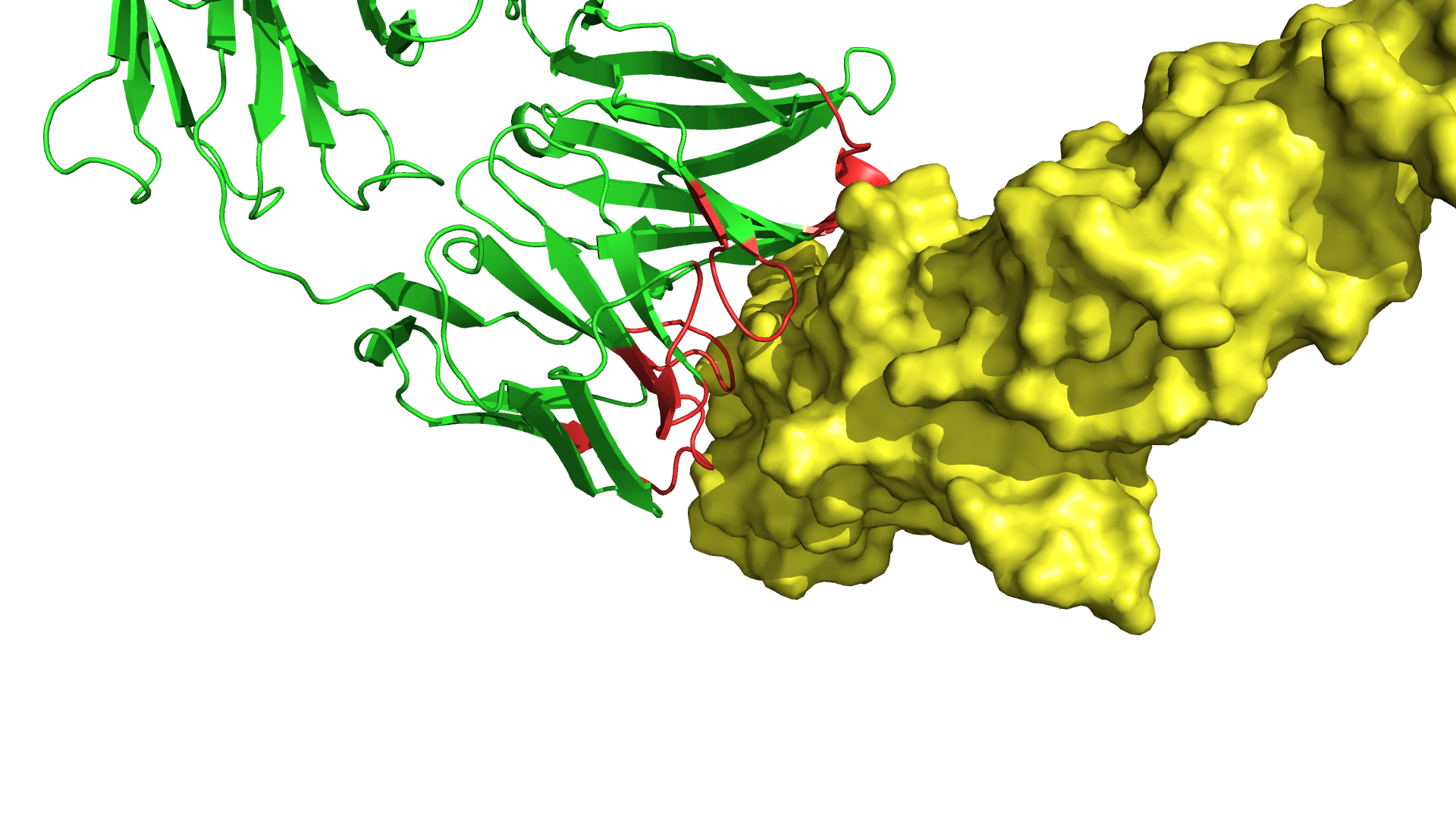
Пример взаимодействия антитела с мишенью. Зелёным цветом показана молекула антитела, жёлтым — молекула мишени. Красным цветом обозначены петли антитела.

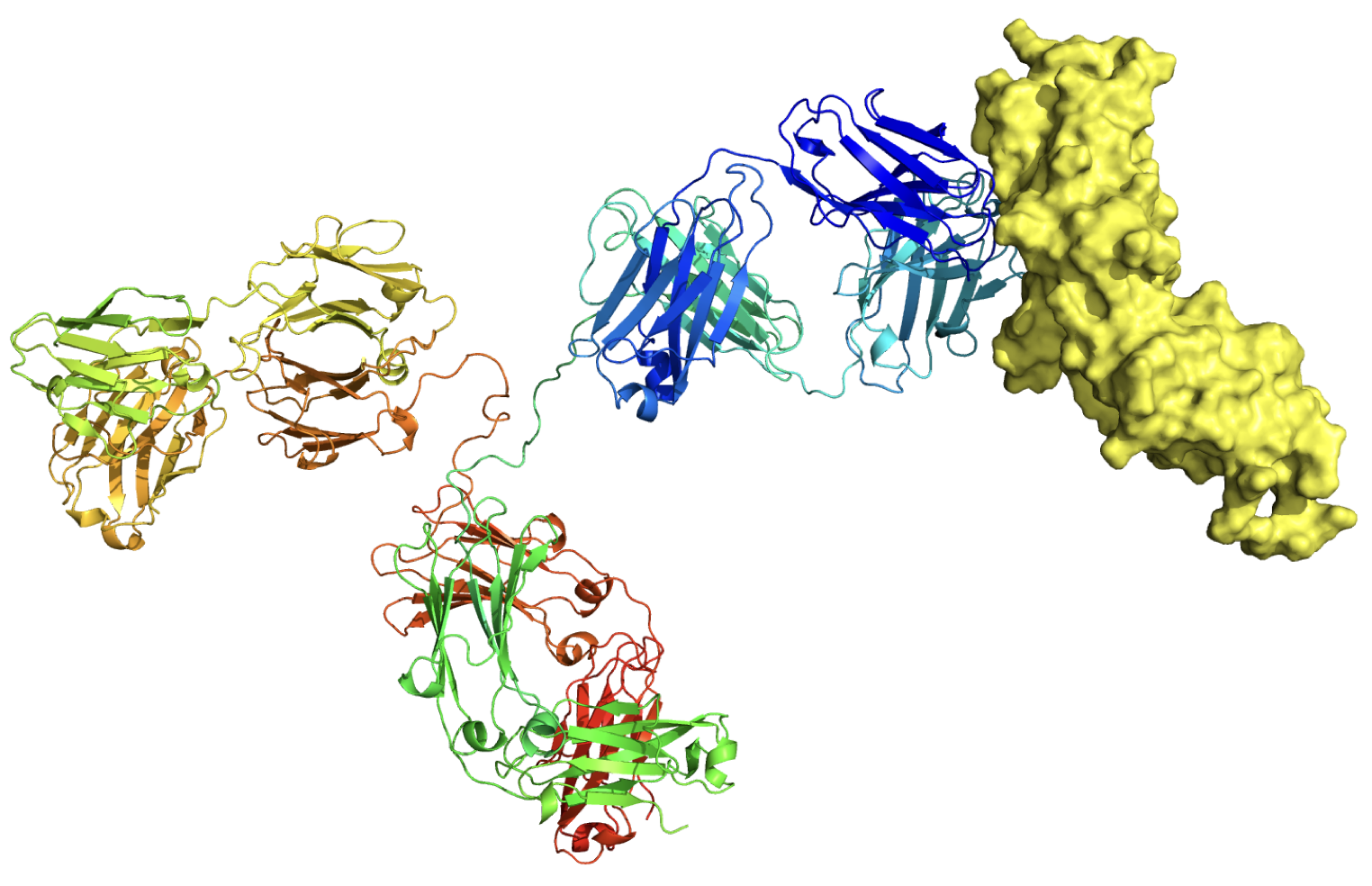
С терапевтической точки зрения очень важно, как именно антитело взаимодействует с целевой молекулой. Известны случаи, когда от места взаимодействия антитела с молекулой зависел характер побочных явлений, вызываемых лекарственным средством. Согласитесь, что когда у вас есть два лекарства, одно из которых точно безопасно для жизни пациентов, а второе — нет, вы будете использовать первое. Зачастую в результате анализа литературы мы имеем представление о том, взаимодействие с какой частью целевой молекулы приведёт к наибольшему терапевтическому эффекту и снижению вероятности возникновения побочных явлений. Поэтому при создании лекарственного средства необходимо убедиться, что оно взаимодействует с целевой молекулой ожидаемым образом.

Тут мы незаметно подходим к уже озвученной выше задаче докинга, заключающейся в предсказании структуры комплекса двух молекул. В нашем случае одной из молекул является лекарство, представляющее собой антитело, а второй молекулой — мишень, с которой антитело должно взаимодействовать в организме человека. Предсказав структуру комплекса антитела и целевой молекулы, мы получим представление о том, с какой частью данной молекулы взаимодействует наше лекарство. На основе этой информации можно будет сделать предварительный вывод о его эффективности. Естественно, реальную эффективность препарата можно оценить только по результатам клинических исследований, но процесс это очень дорогой. Поэтому на такие исследования целесообразно выходить с лекарством, в эффективности которого есть некоторая уверенность.

Принцип работы алгоритмов решения задачи докинга

Как уже было отмечено, задачу докинга можно решить с помощью компьютерного моделирования, и существует множество алгоритмов для её решения вычислительными методами. Мы рассмотрим класс алгоритмов докинга, работающих за счёт перебора положений, в которых одна молекула может находиться относительно другой. Данный класс представляет для нас наибольший интерес не только потому, что принцип работы его представителей прост для понимания, но и потому, что лучший на данный момент алгоритм для автоматического докинга, Piper, принадлежит как раз к рассматриваемому классу алгоритмов.

На вход алгоритм докинга принимает трёхмерные структуры молекул. Вообще говоря, в природе две молекулы могут образовывать разные по структурам комплексы. Поэтому в результате своей работы алгоритм должен предсказать множество структур комплексов, которые могут формировать данные молекулы. Структура молекулы или комплекса представляет собой набор атомов, каждому из которых приписана координата, соответствующая положению этого атома в трёхмерном пространстве.

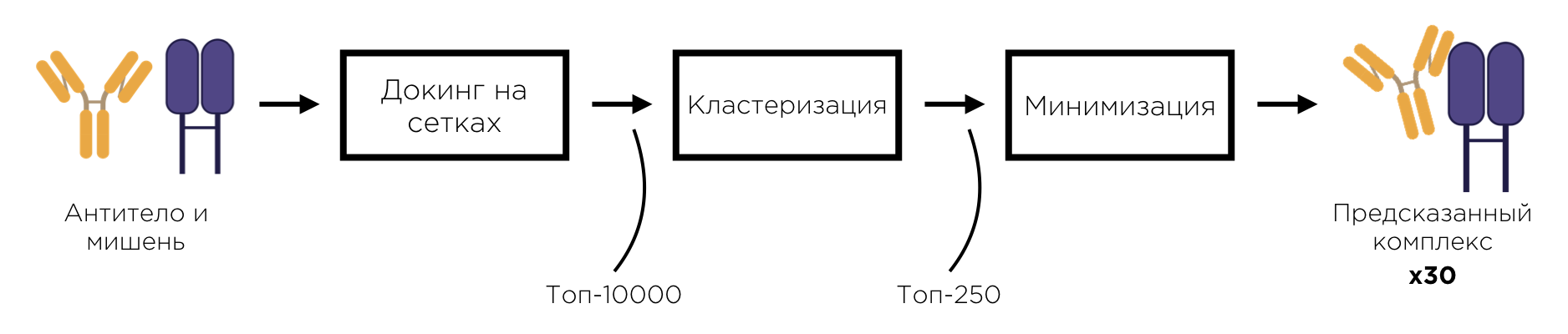
Схема работы алгоритма докинга

Алгоритмы докинга, работающие по принципу перебора положений одной молекулы относительно другой, обычно состоят из трёх последовательных этапов: этапа докинга на сетках, этапа кластеризации и этапа минимизации. Структуры, полученные в результате работы очередного этапа, являются входными данными для следующего этапа. Далее мы рассмотрим каждый из перечисленных этапов подробнее.

Докинг на сетках

Этот этап является основным для алгоритма докинга. В ходе его работы происходит поиск некоторого количества положений молекул относительно друг друга, похожих на природные. В основе данного этапа лежит алгоритм 1992 года за авторством Эфраима Качальского-Кацира (который, помимо того, что был выдающимся учёным, также был четвёртым президентом Израиля).

Положение одной из молекул фиксируется в пространстве. Для второй молекулы с фиксированным шагом перебираются все возможные вращения относительно первой молекулы. Для каждого вращения второй молекулы перебираются все её смещения относительно первой, которая остается неподвижной. В итоге отбирается некоторое количество комплексов, наиболее похожих на природные и состоящих из фиксированной первой молекулы и повёрнутой и смещённой второй.

Если высокоуровнево описать принцип работы алгоритма докинга на сетках, то получается совсем простой код:

complexes = []

# перебираем все возможные вращения второй молекулы относительно первой
for rotation in rotations: 
    # перебираем все возможные смещения второй молекулы относительно первой
    for shift in shifts: 
        # поворачиваем и сдвигаем вторую молекулы 
        # с учётом заданных вращения и смещения
        moved_mol2 = rotate_and_shift(mol2, rotation, shift) 

        # создаём из молекул комплекс, в котором вторая 
        # молекула повёрнута и сдвинута
        new_complex = (mol1, moved_mol2) 

        complexes.append(new_complex)

# сортируем все полученные комплексы по их правдоподобию
complexes.sort(lambda candidate_complex: score_complex(candidate_complex)) 

Однако тут важны детали. А именно, нас интересует способ оценки правдоподобия молекулярного комплекса, то есть того, насколько вероятно существование этого комплекса в природе. Точное определение правдоподобия даже одного молекулярного комплекса — задача достаточно трудоёмкая. Всего у нас получается комплексов, где R — число вращений второй молекулы, а S — число её смещений. На практике имеет порядок . Определить правдоподобие такого большого числа комплексов за разумное с практической точки зрения время и в условиях ограниченности вычислительных ресурсов просто не представляется возможным.

В 1992 году, когда был изобретён алгоритм докинга на сетках, проблема производительности была ещё более актуальна. Поэтому его авторами был предложен следующий подход.

Основная идея алгоритма заключалась в том, чтобы поместить обе молекулы, структуру комплекса которых мы хотим предсказать, в дискретные трёхмерные сетки. В оригинальной статье предлагалось заполнять ячейки сетки по следующей формуле:

Значение 1 присваивается ячейкам сетки, которые содержат атомы, находящиеся на поверхности молекулы. Значение , которое находится в промежутке от 0 до 1, присваивается ячейкам, которые содержат только атомы молекулы, не имеющие доступа к её поверхности. Значение 0 присваивается всем остальным ячейкам сетки. Пример построения сеток для двух молекул приведён ниже.

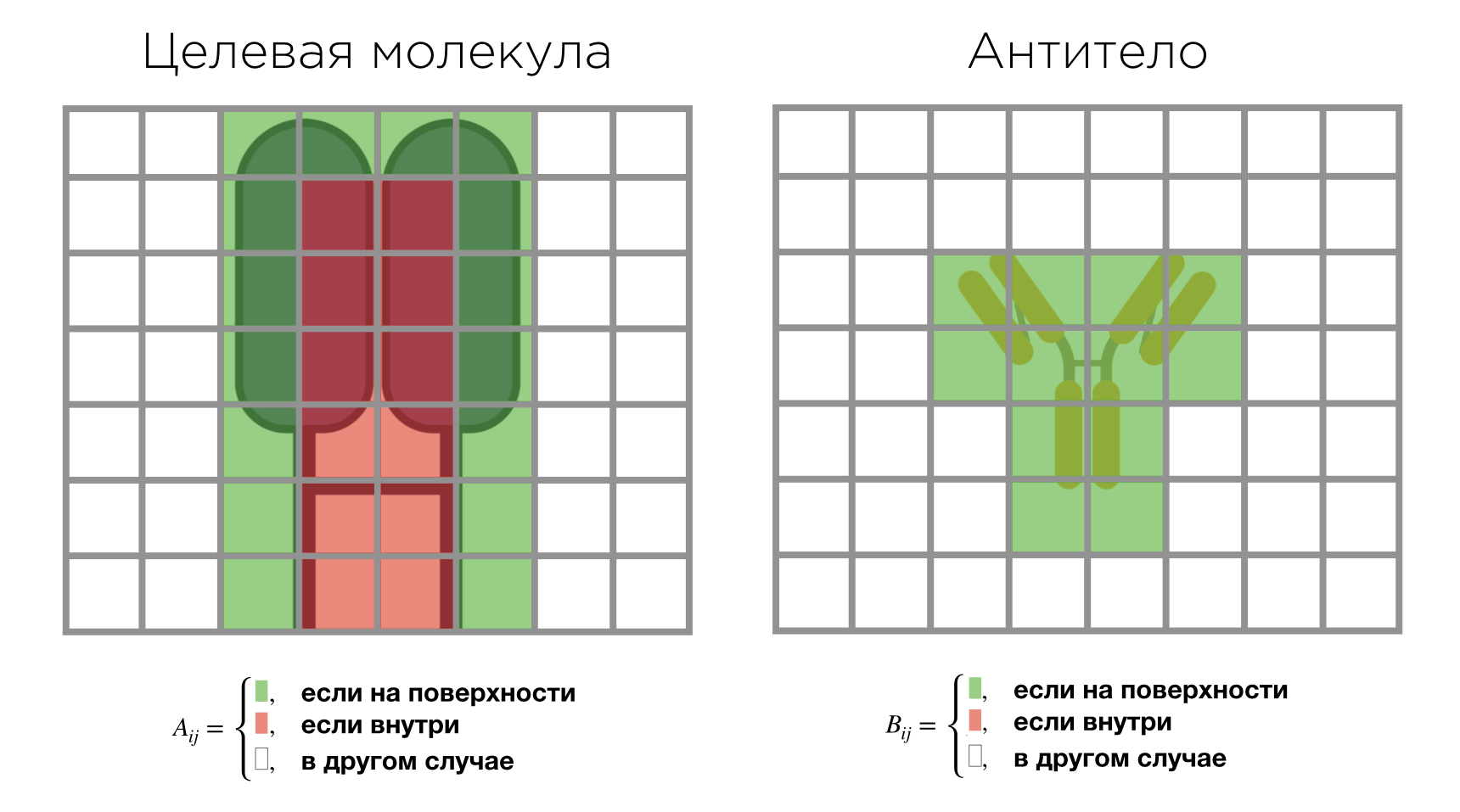
Пример построения двумерных корреляционных сеток для двух молекул

Теперь давайте введём понятие корреляции двух сеток. Фактически, корреляция сеток представляет собой их поэлементное перемножение и последующее суммирование результатов перемножения. Давайте посмотрим, как ведёт себя корреляция двух сеток, построенных по описанной выше формуле. Наибольший вклад в корреляцию даёт перемножение ячеек, значения которых равны 1. Это соответствует ситуации, когда и в первой, и во второй сетках в ячейках находятся атомы, принадлежащие поверхностям молекул. Получается, что чем больше корреляция двух сеток, тем более подходящими друг другу с точки зрения геометрии поверхностей являются молекулы.

Можно предположить, что наиболее правдоподобные молекулярные комплексы имеют высокую геометрическую совместимость. Тогда получается, что мы можем описать правдоподобие комплекса, образуемого двумя молекулами, через корреляцию сеток молекул, входящих в его состав.

Однако в таком виде данная идея не даёт нам прироста производительности: корреляция двух сеток вычисляется за время , где N — размер одного измерения сетки, и время работы алгоритма всё ещё будет составлять . Это много. Заметим, что теперь нам не надо искать смещение второй молекулы относительно первой. Смещение молекул мы описываем исключительно в терминах сеток и их корреляции, поэтому достаточно найти смещение сетки второй молекулы относительно сетки первой молекулы. По найденному смещению можно однозначно восстановить сдвиг второй молекулы относительно первой. Теперь можно более точно оценить время работы текущего алгоритма: оно получилось . Но это очень много, учитывая, что приемлемая точность работы алгоритма достигается при N, имеющем порядок .

Тут нам наконец-то приходит на помощь университетская программа курса по алгоритмам. Оттуда мы знаем (или ещё только узнаем), что корреляция двух трёхмерных сеток может быть вычислена за время для всех циклических сдвигов одной сетки относительно другой. Делается это с помощью алгоритма быстрого преобразования Фурье, более известного как FFT. При таком подходе время работы алгоритма докинга на сетках составляет , что является намного более приемлемым результатом, чем время работы первоначального подхода.

Наконец-то мы можем записать финальную эффективную версию алгоритма докинга на сетках:

complexes = []

# строим корреляционную сетку для первой молекулы
grid_for_mol1 = build_grid(mol1) 

# прямое преобразование Фурье для первой молекулы
fft_mol1 = fft_3d(grid_for_mol1) 

# перебираем все возможные вращения второй молекулы относительно первой
for rotation in rotations: 
    # поворачиваем вторую молекулу с учётом заданного вращения
    rotated_mol2 = rotate(mol2, rotation) 

    # строим корреляционную сетку для повёрнутой второй молекулы
    grid_for_mol2 = build_grid(rotated_mol2) 

    # прямое преобразование Фурье для второй молекулы
    fft_mol2 = fft_3d(rotated_mol2) 

    # поэлементно перемножаем преобразованные сетки. После этого 
    # применяем к результату перемножения обратное преобразование 
    # Фурье. И, казалось бы, магическим образом получаем корреляции 
    # для всех циклических сдвигов второй сетки относительно первой
    correlations = ifft_3d(fft_mol1 * fft_mol2) 

    # создаём из молекул комплексы, в которых вторая 
    # молекула повёрнута и сдвинута
    rotation_complexes = map(lambda shift_: (mol1, shift(rotated_mol2, shift_))) 

    # для каждого комплекса мы уже посчитали его правдоподобие 
    # с помощью быстрого преобразования Фурье
    complexes += list(zip(rotation_complexes, correlations)) 

# сортируем все полученные комплексы по их правдоподобию
complexes.sort(lambda (candidate_complex, score): score) 

Тут интересно то, что именно в таком виде алгоритм докинга на сетках используется и по сей день. Все улучшения, которые делаются для повышения точности его работы, затрагивают исключительно способы построения корреляционных сеток, а высокоуровневая структура алгоритма остаётся неизменной.

Улучшение докинга на сетках за счёт статистического потенциала

Алгоритм докинга на сетках бесконечно крут своей простотой и красотой, однако в том виде, в котором он описан выше, алгоритм имеет низкую точность. Дело в том, что на практике одной лишь геометрической совместимости поверхностей молекул не достаточно для того, чтобы делать выводы о правдоподобии формируемого ими комплекса.

Исследователи быстро это заметили и предложили способы учёта дополнительной информации при формировании корреляционных сеток молекул. Так, современные алгоритмы докинга на сетках учитывают информацию об энергии вандерваальсовых и электростатических взаимодействий между атомами и, если речь идёт о докинге антител, информацию о том, где у молекулы расположены петли.

Однако лучший на сегодняшний день алгоритм докинга, Piper, пошёл дальше своих аналогов и предложил способ учёта в процессе докинга на сетках информации о статистическом потенциале. Статистический потенциал — это набор чисел, который описывает энергии взаимодействия конкретных пар атомов, рассчитанные на основе экспериментальных данных. Энергия молекулярного комплекса в заданном потенциале вычисляется по следующей формуле:

где и — множества атомов молекул данного комплекса, а — энергия взаимодействия атомов типов и в статистическом потенциале .

Это выражение можно представить в виде корреляции двух сеток, что позволяет повысить точность работы алгоритма докинга на сетках. Я был бы рад поделиться теоретическими выкладками о том, как это сделать, но хочется успеть рассказать вам о более интересных вещах. Просто поверьте (или проверьте), что для понимания этих выкладок не нужно ничего, кроме пары фактов из курса линейной алгебры.

Создание статистических потенциалов с разными свойствами представляет большой простор для исследований. Например, один только Piper использует два разных потенциала: DARS (Decoys as Reference State) и aADARS (asymmetric Antibody DARS). aADARS используется для докинга антител, а DARS — для докинга остальных видов молекул.

В рамках своей магистерской работы я занимался созданием нового статистического потенциала, предназначенного именно для докинга антител. Изначально предполагалось просто обновить aADARS, пересчитав его на новых экспериментальных данных. Однако в ходе работы выяснилось, что сам подход к созданию потенциала может быть существенно улучшен за счёт учёта информации про электростатические взаимодействия атомов и петли антител. Это привело к созданию нового статистического потенциала — WAASP (Widely Applicable Antibody Statistical Potential). Использование WAASP существенно увеличило точность алгоритма докинга HEDGE, разрабатываемого в департаменте, в котором я работаю:

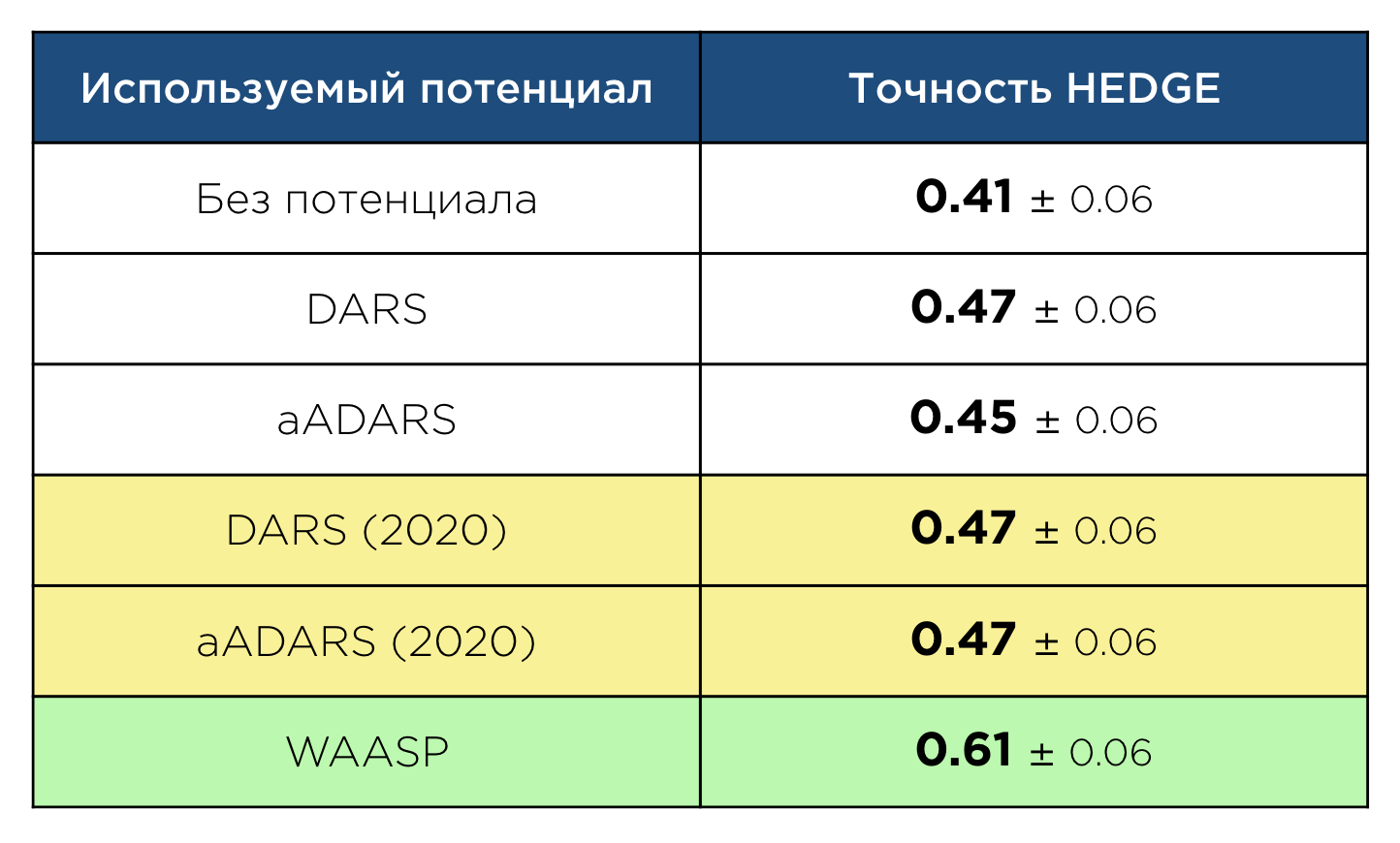
Сравнение версий алгоритма докинга HEDGE, использующих разные статистические потенциалы

Что важно, прирост точности является существенным не только относительно версии алгоритма, не использующей статистические потенциалы, но и относительно версий, использующих DARS и aADARS.

Если вам интересно узнать побольше про применение статистических потенциалов в контексте задачи докинга, то на сайте нашей магистратуры есть запись моей защиты (вообще говоря, не только моей). Всего 7 минут, и ваш кругозор расширится необратимым образом!

Кластеризация

Напомню, что кластеризация является следующим этапом работы алгоритма докинга после докинга на сетках. Наличие этого этапа обусловлено тем, что точность докинга на сетках, пусть даже использующего все возможные улучшения, всё ещё оставляет желать лучшего. Зачастую необходимо рассмотреть топ-10000 комплексов, полученных в результате работы докинга на сетках, чтобы найти правильный ответ. А просто отдать пользователю все 10000 комплексов как результат работы алгоритма докинга нельзя, потому что без дополнительного анализа никакой содержательной информации из этого объёма данных получить не удастся.

Основной задачей этапа кластеризации является уменьшение количества кандидатов на правильный ответ. В основе данного этапа лежит достаточно сильное, но необходимое предположение: комплексы, похожие на природные, появляются в результатах работы докинга на сетках чаще остальных. Из этого предположения следует, что результаты работы докинга на сетках разбиваются на несколько больших групп и некоторое количество групп поменьше. Каждая большая группа комплексов соответствует результатам, похожим на определённый природный комплекс, который данные молекулы могут формировать. Маленькие группы соответствуют комплексам, которые попали в результаты работы докинга на сетках по причине его низкой точности и никакие природные комплексы не представляют.

Разбиение множества элементов на группы по принципу сходства элементов называется кластеризацией. Каждая полученная группа называется кластером. В нашем случае в качестве разбиваемого на группы множества выступает множество результатов работы алгоритма докинга на сетках. В качестве метрики сходства элементов множества выбирается классическая для задач структурной биоинформатики метрика RMSD (Root-Mean-Square Deviation). RMSD между двумя молекулярными комплексами вычисляется как среднеквадратичное отклонение координат атомов одного комплекса от координат атомов другого.

Определив множество, которое мы хотим разбить на группы, и метрику похожести его элементов, мы можем воспользоваться любым существующим алгоритмом кластеризации, чтобы решить поставленную задачу. Опять же, чему нас учили в вузе: если не знаешь, какой алгоритм кластеризации взять, возьми иерархическую кластеризацию — точно не прогадаешь. Действительно, данный алгоритм очень прост для понимания и гибок в плане настройки своих параметров. Правильную комбинацию параметров можно подобрать при условии наличия выборки, на которой можно произвести настройку алгоритма. На практике оказывается, что алгоритм иерархической кластеризации действительно хорошо подходит для разбиения на группы множества молекулярных комплексов.

После кластеризации отбирается порядка 250 кластеров, имеющих наибольший размер. Для каждого полученного таким образом кластера вычисляется центроид — представитель кластера, наименее удалённый от остальных его элементов. Таким образом, мы смогли уменьшить количество кандидатов на правильный ответ с 10000 до 250, однако это всё ещё довольно много. Улучшить данный результат нам поможет следующий этап работы алгоритма докинга.

Минимизация

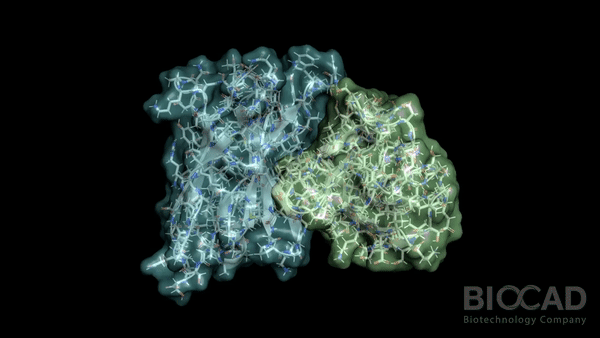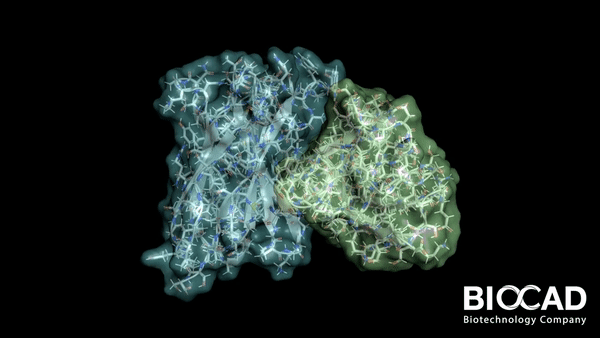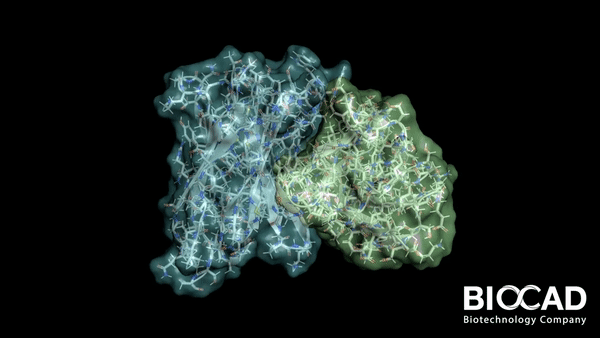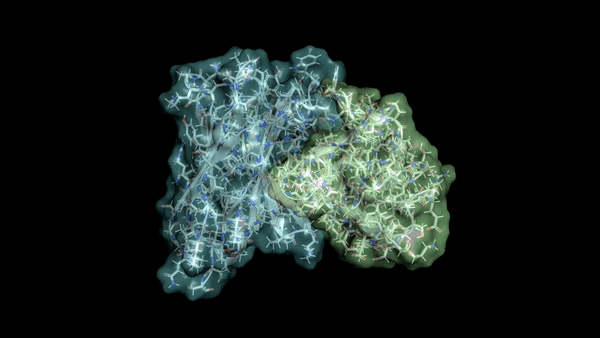
Минимизация структуры молекулярного комплекса

Заключительным этапом работы алгоритма докинга является этап минимизации. Давайте разбираться, почему он так называется и как он работает!

Сначала давайте поймём, что такое энергия комплекса с точки зрения структурной биоинформатики. Возьмём две молекулы, которые формируют данный комплекс, и разведём их на бесконечное расстояние друг от друга. После этого давайте отпустим эти молекулы и понаблюдаем за нашей системой. Если молекулы слиплись в комплекс сами собой, то это значит, что его образование им выгодно. Если молекулы так и остались болтаться, никак друг с другом не взаимодействуя, то можно прицепить их друг к другу, используя внешнее воздействие (например, наши руки, которыми мы уже умудрились раздвинуть молекулы на бесконечное расстояние друг от друга!). Однако это означает, что в природных условиях данные молекулы в комплекс не объединятся.

В итоге энергией комплекса называется количество работы, которую нужно совершить над системой для того, чтобы привести её из состояния, когда две молекулы находятся на бесконечном расстоянии друг от друга, к виду, когда две молекулы сцеплены и формируют данный комплекс. Ситуация, когда две молекулы слипаются в комплекс сами собой, соответствует случаю отрицательного значения энергии: нам не то что не потребовалось двигать молекулы — они сами могли бы подвигать что-нибудь, например, маленькую турбину! Ситуация, когда нам всё-таки нужно прикладывать к системе внешние силы, чтобы сцепить молекулы, соответствует случаю положительной энергии.

Отсюда следует вывод, что чем меньше значение энергии комплекса, тем наиболее вероятно его существование в природе: мы так определили энергию. Из этого вывода мы можем почерпнуть две простые, но важные идеи.

Во-первых, если мы сможем уменьшить величину значения энергии какого-то комплекса, то тем самым повысим вероятность его существования в природе. Во-вторых, целесообразно отдавать в качестве результата работы алгоритма докинга комплексы, имеющие наименьшие значения энергии, так как их существование, опять же, наиболее вероятно.

Существуют подходы, позволяющие приближённо оценивать энергии молекулярных комплексов. Одним из таких подходов является использование силовых полей. Фактически, силовое поле есть функция от атомов комплекса, значение которой соответствует энергии данного комплекса, вычисленной с некоторой погрешностью.

У функции энергии есть минимальное значение, которое достигается при определённом расположении атомов комплекса относительно друг друга. Так как энергия комплекса при данном положении атомов является минимальной, то с большой вероятностью структура такого комплекса близка к природной. Таким образом, чтобы приблизить структуру комплекса-кандидата, полученного в результате докинга на сетках и кластеризации, к её природному виду, нам надо найти положение атомов комплекса, при котором энергетическая функция достигает своего минимума.

Процесс поиска минимума функции называется минимизацией. Отсюда и название данного этапа работы докинга!

Минимум функции нас с вами научили искать ещё в школе: ну что там, посчитай производную, найди точки, в которых она обращается в ноль, посмотри на значения функции в окрестностях этих точек — победа! В общих чертах идея поиска минимума энергетической функции остаётся такой же. Однако сложностей тут добавляет то, что у нашей функции не одна переменная (как, например, в случае со школьной параболой), а очень много: фактически, каждая координата каждого атома является параметром функции.

Для решения задачи минимизации многопараметрической функции энергии в биоинформатике принято применять градиентные методы. Если совсем просто, то градиент функции — многомерный аналог производной. Градиент представляет из себя вектор, направление которого показывает направление наискорейшего роста функции. В точке минимума функции модуль вектора градиента близок к нулю аналогично тому, когда в точке минимума однопараметрической функции её производная равняется нулю.

Однако аналитически найти такой набор параметров функции, при котором её градиент обращается в ноль, невозможно: параметров очень много. Поэтому минимум функции ищется численно. На протяжении некоторого количества итераций параметры функции смещаются в направлении, обратном направлению градиента: градиент показывает, в какую сторону растёт функция, соответственно, убывает она в обратном направлении. В конце концов мы придём к такому набору параметров, при котором функция достигает своего минимума.

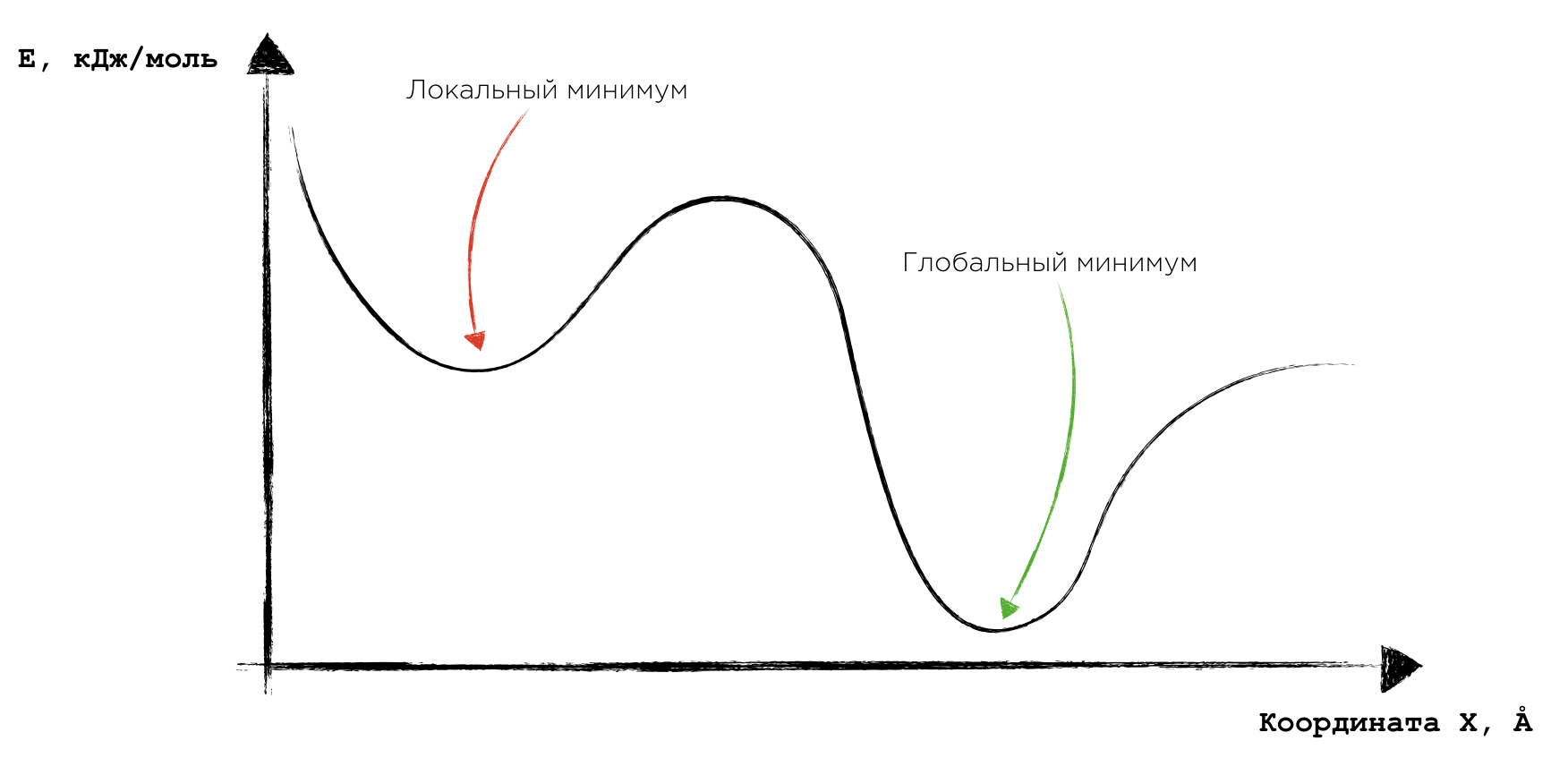
Пример ситуации, когда локальный минимум функции энергии не является глобальным

Нюанс тут заключается в том, что данный минимум является локальным. В некоторой окрестности данной точки действительно нет набора параметров, при котором значение функции было бы меньше. Но это верно лишь для данной окрестности: где-нибудь подальше очень легко может найтись значение функции, которое меньше данного (пример такой ситуации изображён на соответствующем рисунке). И это, несомненно, проблема. Обычно её решают за счёт добавления в процесс минимизации функции некоторой случайности, которая помогает выйти из локального минимума и продолжить поиск минимума глобального.

В итоге в процессе этапа минимизации мы делаем следующее. Для каждого комплекса, полученного в результате кластеризации, мы изменяем положение координат его атомов таким образом, чтобы энергия комплекса достигла своего минимума. После этого мы ранжируем полученных кандидатов по величине значения энергии и отдаём пользователю 30 комплексов, образование которых является наиболее выгодным с энергетической точки зрения.

Всё, процесс работы всего алгоритма докинга завершён!

Заключение

В этой статье мы с вами разобрали, зачем нужно уметь решать задачу предсказания структуры молекулярного комплекса и как её решают сейчас.

Сама по себе задача докинга очень важна потому, что её точное и быстрое решение обеспечит серьёзное увеличение скорости создания новых лекарственных средств. Существующие подходы к решению задачи на регулярной основе помогают биоинформатикам и структурным биологам создавать инновационные лекарства. Однако текущие алгоритмы докинга всё ещё далеки от идеала, так как требуют большого объёма ручной работы при обработке результатов. Тем не менее это не повод опускать руки: область по-прежнему таит в себе уйму интересных задач и ждёт новых прорывных открытий!

Но даже текущий прогресс в области алгоритмов докинга не был бы возможен, если бы у людей, работающих над решением этой задачи, не было широкого математического (да и жизненного, чего уж там) кругозора. Использование быстрого преобразования Фурье для поиска оптимальных смещений одной сетки относительно другой, кластеризация трёхмерных структур, минимизация функции с помощью градиентных методов — все эти идеи достаточно абстрактны. Нужно уверенно владеть соответствующими методиками, чтобы увидеть возможность их использования в практической задаче, а затем корректно (это очень важно!) их применить.

Идеальное высшее образование действительно должно давать студенту и широкий кругозор, и уверенность в полученных знаниях, и умение корректно применять эти знания на практике. Увы, как и любой другой, данный идеал не достижим. Однако это не мешает некоторым образовательным программам к нему стремиться. У нас как раз такая программа. Поэтому если вы хотите стать классным специалистом в области прикладной математики и в будущем заниматься решением сложных, интересных и актуальных задач, то наша программа — понятный и серьёзный шаг на пути к достижению этой цели.

Автор: Екатерина

Источник