Современные методы биоинформатики позволяют довольно точно восстанавливать эволюционные истории на основании последовательностей генов или белков ныне живущих организмов. А благодаря технологиям секвенирования нового поколения последовательности производятся быстрее, чем их успевают анализировать. Вот только эволюционная реконструкция – дело вычислительно дорогое и неплохо бы уметь получать репрезентативные выборки пригодного для анализа размера. Как это сделать и что вообще такое в данном случае “репрезентативная” – под катом.
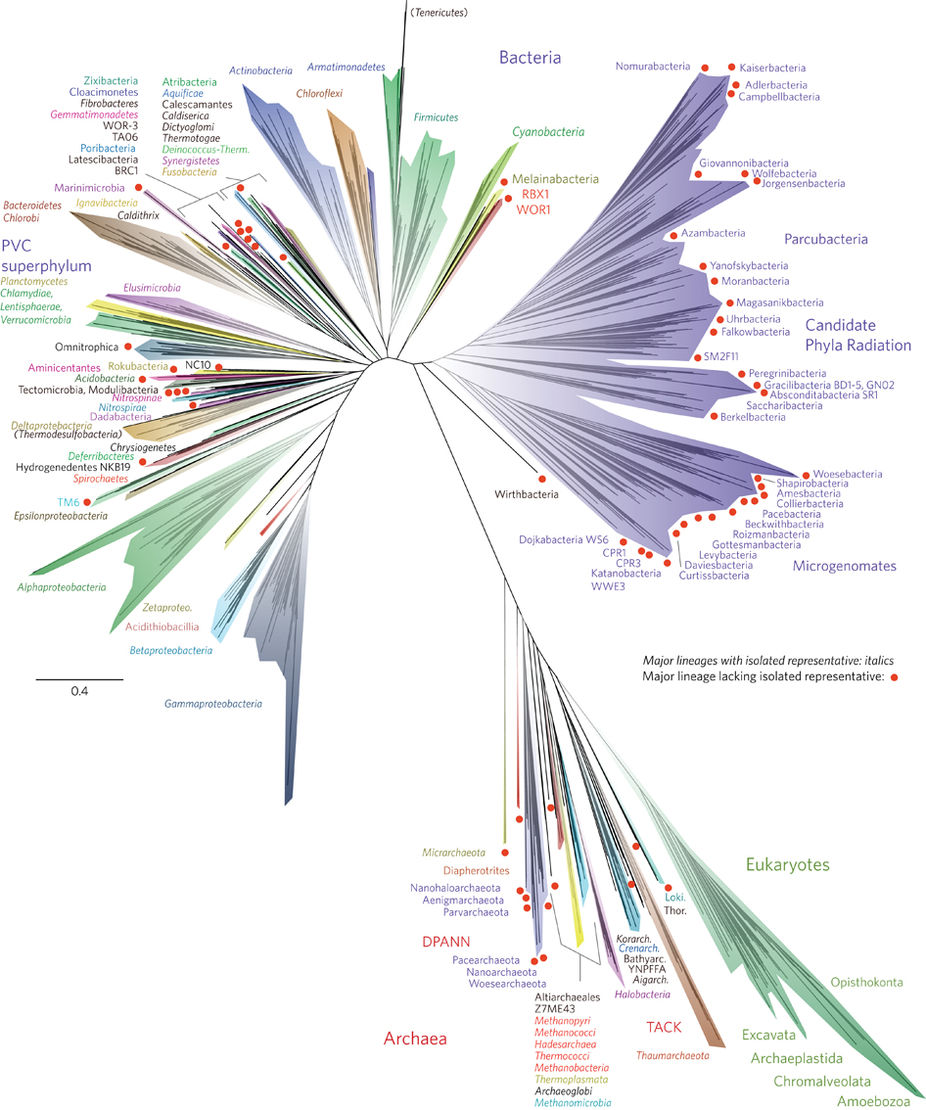
Красными кружками, кстати, выделены группы одноклеточных организмов, которые никто никогда не видел. Ни в одной лаборатории в чашках Петри или хитроумных биореакторах не растёт культура. Об их существовании стало известно только в последние годы из метагеномных исследований, когда из среды выделяют всю ДНК, какая есть, и всю разом анализируют. Но это так, к слову. Картинка включена в статью исключительно как самое потрясающее дерево за последние годы и для понимания статьи не важна.
Что нужно сделать
Прежде всего сформулируем чётко, что происходит и чего мы пытаемся добиться. Мы хотим узнать, откуда взялся и как эволюционировал тот или иной ген, скажем, человека. Или картошки, или одноклеточной водоросли, методы для любого организма будут примерно одинаковые. В биологических базах данных можно найти родственные ему последовательности других организмов, засунуть их в некую магическую программу и получить на выходе филогенетическое древо. Проблема в том, что родственных последовательностей, скорее всего, будут тысячи. А строительство филогенетических деревьев методами максимального правдоподобия или байесовской филогенетики – NP-полная задача и решение состоит, грубо говоря, в переборе разных деревьев и параметров эволюционной модели. У меня обычно уходит от пары суток до недели на 2 16-ядерных процессорах AMD Opteron 6276 c 64 Gb оперативки для нескольких сот генов средней длины. Есть и полиномиальные методы филогенетического анализа, но они менее точны и опубликовать основанную на них статью в приличном журнале будет нереально.
Значит, нужно взять из этого набора корректную выборку: выделить относительно небольшой набор последовательностей заданного размера и делать из него выводы обо всей совокупности. Далее будет использоваться кое-какая филогенетическая терминология, объяснения – под спойлером.
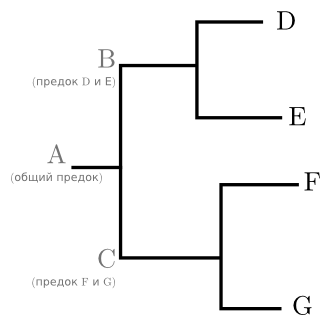
К примеру (рисунок ниже): когда-то существовал предковый ген A, у которого были потомки B и С. B оставил потомков D и E, а C – F и G. Наблюдаются только четыре последовательности D, E, F и G; предки от A до C существовали когда-то давно и к нашим дням исчезли. Соответственно, рассуждать о них мы можем исключительно на основании современных последовательностей и преимущественно в терминах типа “общий предок такого-то, такого-то и такого-то”. Часть дерева, объединённая общим предком, называется кладой. Этот термин может применяться как к собственно части графа, так и к находящимся на её концах последовательностям. В дереве на рисунке, например, есть клады (D, E) и (F, G). Хотя номинально клад в дереве столько же, сколько внутренних узлов, обычно исследователя интересует только несколько клад, значимых для его работы.
Можно спросить: почему я говорю об эволюции последовательностей, хотя все привыкли думать об эволюции видов. В конце концов, питаются, размножаются и вымирают целые организмы, а не небольшие кусочки ДНК. Это, в общем, верно. “Древо жизни” было изначально придумано для видов, и филогенетические деревья прекрасно описывают их эволюцию. Но есть две причины обсуждать деревья именно последовательностей: во-первых, филогенетика как область биоинформатики чаще всего имеет дело с последовательностями. Эволюция организмов с совокупностью признаков – запутанный и сложно формализуемый процесс, к тому же происходивший миллионы лет назад под влиянием неизвестно каких факторов и вообще не очень понятно с кем. Споры о том, какой именно была первая эукариота, например, вряд ли кончатся до изобретения машины времени. С другой стороны, замена, вставка и удаление букв в строке вполне поддаются математическому моделированию.
Во-вторых, эволюция отдельного гена может отличаться от эволюции видов, у которых он представлен. На дереве выше описан простейший сценарий – у общего предка исследуемых видов была одна копия исследуемого гена, и в течение эволюции она просто передавалась по наследству, постепенно накапливая мелкие мутации. Такие гены приходятся друг другу ортологами. По определению, ортологи – это гены разных видов, восходящие к единому гену их общего предка.
Но предположим, что у предка С произошла дупликация исследуемого гена. Был один ген, а стало два одинаковых, которые начали наследоваться и мутировать независимо друг от друга. Вероятно, что одна из копий гена продолжила делать то же, что и раньше, а вторая (раз её старую функцию и без неё есть кому выполнять) мутирует и принесёт виду какое-нибудь новое преимущество. А вот вид Е или кто-то из его недавних предков этот ген утратил вовсе. Такое бывает, если ген не то чтоб жизненно необходим. Хотя взаимоотношения видов не менялись, дерево примет следующий вид:
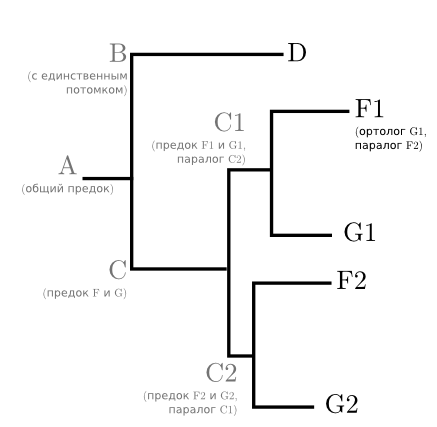
На основании этого дерева уже довольно сложно рассуждать об эволюции видов. E нет вовсе, а F и G встречаются по два раза каждый. Зато оно позволяет понять, когда появились гены *1 и *2 и насколько далеко они разошлись. Гены F1 и G1 приходятся друг другу паралогами – генами одного вида, восходящими к единственному гену его предка.
Кроме дупликаций и делеций, случаются и другие события: иногда гены приобретаются организмами не от родителей, а от других, не родственных, организмов (называется горизонтальный перенос генов или HGT), иногда в один ген добавляется кусок из какого-нибудь другого гена или, наоборот, кусок отрезается, иногда несколько генов объединяются в один. Много чего интересного, в общем, происходит. Так что заранее не известно, какой результат получится, если закинуть в анализ все гомологичные последовательности.
Определим “корректную выборку” следующим образом: пусть в дереве, включающем все последовательности из набора, есть некоторое количество интересующих нас клад. Каков их биологический смысл, неважно; главное, что они в основном монофилетичны (то есть восходят к единственному предку каждая) и в основном отделены более-менее длиннной ветвью от остального дерева. Каждой кладе соответствует подмножество входящих в неё последовательностей. Корректной выборкой будем считать такую, что каждое из этих подмножеств представлено в ней как минимум одной последовательностью.
Чего мы делать не будем
Самая очевидная идея – взять последовательности случайным образом и надеяться, что выборка будет более-менее корректной. Но случайность – она и есть случайность; может, будет корректной, а может, и нет. На практике скорее всего не будет, потому что изучается биосфера неравномерно. Человек и ряд модельных объектов (мушка дрозофила, пекарские дрожжи, кишечная палочка Escherichia coli и т.п.) исследуются очень подробно и для них многократно отсеквенировано всё, что только можно. Экономически или медицински значимые объекты (например, рис и ВИЧ) и ближайшие родственники значимых объектов (например, приматы как родственники человека) исследованы чуть похуже, но тоже очень хорошо. А вот одноклеточный планктон, как бы он ни был разнообразен, мало для кого представляет особый интерес и секвенируется относительно редко. Поэтому в наборе из 100 гомологичных генов вполне может оказаться 30 последовательностей животных, 30 последовательностей растений, 20 последовательностей грибов и по одной-две последовательности всех остальных эукариотических групп.
Для случайной выборки соотношение численности групп в целом сохранится. А ведь нам отнюдь не нужно его сохранять, оно всё равно отражает скорее количество занимающихся тем или иным таксоном учёных и их финансирование, чем какую-то биологическую реальность. Нам нужно охватить как можно больше групп, включая малочисленные.
Окей, следующая идея – раз у нас уже есть таксономическая метаинформация (какому организму принадлежит какая последовательность), почему бы ей не воспользоваться? Возьмём один ген человека, возьмём более-менее равномерно десяток генов других животных, десяток генов грибов и так далее. Идея неплохая, люди так делают, но не универсальная. Если все гены в исходном наборе являются друг другу ортологами, то есть их эволюция полностью совпадает с эволюцией их хозяев, то лучше всего так и поступить. Но это далеко не всегда так. Взгляните, например, на рисунок:

Это эволюция хитинсинтаз (белков, отвечающих за синтез хитина) из нашей позапрошлогодней статьи. Как видно, белки грибов (Fungal class *) не формируют единой клады; вместо этого они разбросаны по двум разным концам дерева. То же самое происходит и с другими организмами: например, большинство видов оомицет имеет по одному гену из каждой из четырёх оомицетных клад. Даже если принять для простоты, что клад всего две, их всё равно необходимо учитывать.
Условный “десяток генов грибов” не должен быть десятком генов одной из клад, это должны быть несколько генов из одной клады и несколько из другой. То же самое верно и для остальных групп.
У хитинсинтаз довольно запутанная эволюция, и для большинства генов дерево будет значительно проще. Но сложность дерева нельзя оценить до того, как оно будет построено, и поэтому универсальный метод выборки должен уметь работать и с такими данными.
Наконец, идея третья. Где-то в начале вскользь упоминались быстрые и менее надёжные методы филогенетического анализа. Почему бы не построить с их помощью какое-нибудь дерево, не выделить в нём клады и не брать выборку уже из них? Да, дерево будет не очень точным, но скорее всего оно будет более-менее похоже на истинное. Можно сделать выборку на основании такого дерева, а уже её обсчитать как следует. В таком виде идея не очень практична, потому что “выделить клады” – задача нетривиальная. Выше я упоминал, что клад вообще-то столько же, сколько и узлов в дереве, и заранее неизвестно, какие из них интересуют пользователя. Но от этой идеи можно отталкиваться.
Что мы будем делать
Один из самых распространённых способов быстро получить дерево – это построить для последовательностей матрицу дистанций (а метрик дистанции для биологических последовательностей очень много разных) и на её основании построить дерево каким-нибудь NJ или UPGMA. Конечно, построение матрицы дистанций квадратично по времени и памяти от числа последовательностей, но в отличие от ML- или байесовской филогенетики оно хотя бы полиномиально.
Даже не строя дерево, на основании матрицы дистанций можно получить такую выборку, которая будет включать как можно более разнообразные последовательности. Поскольку последовательности в любой кладе по определению больше похожи друг на друга, чем на другие последовательности, такой метод должен охватить большинство клад. Алгоритм довольно простой: включаем в выборку произвольную последовательность, для каждой из оставшихся запоминаем дистанцию до неё. Потом включаем в выборку ту из оставшихся, для которой эта дистанция максимальна, для остальных запоминаем дистанцию и до неё тоже. Потом из оставшихся выбираем ту, у которой самая большая минимальная дистанция до одной из последовательностей в выборке, добавляем её в выборку и запоминаем дистанцию. Повторять, пока выборка не достигнет желаемого размера. За сходство с алгоритмом Neighbour Joining этот метод мы назвали Distant Joining. В коде это выглядит вот так:
leader = not_sampled[0]
reduced_list.append(leader)
minima = {x: dist(leader, x) for x in not_sampled[1:]}
while len(reduced_list) < final_count:
leader = max(minima.items(), key=lambda a: a[1])
reduced_list.append(leader[0])
del minima[leader[0]]
not_sampled.remove(leader[0])
for i in not_sampled:
d = self[(leader[0], i)]
if d < minima[i]:
minima[i] = d
Или картинкой:
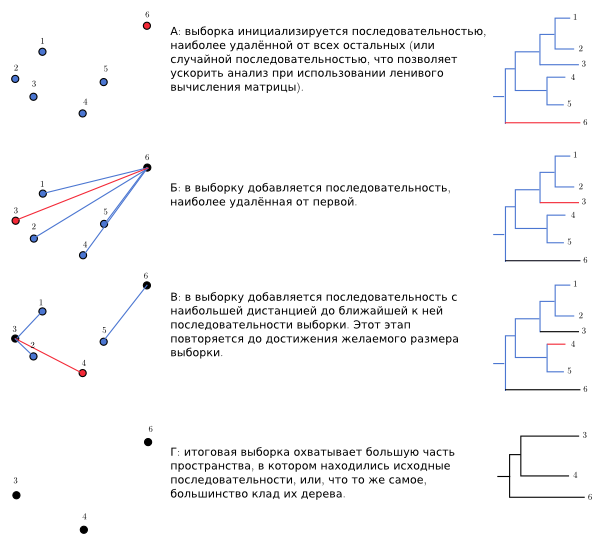
Красным – добавляемое на данной итерации, чёрным – уже добавленное.
Как оказалось, описанный метод работает довольно неплохо. Вот результаты на тысяче симулированных наборов последовательностей (синий – Distant Joining, чёрный – RS, случайный выбор, красный – SS, выбор скольки-то последовательностей, ближайших к заданной):
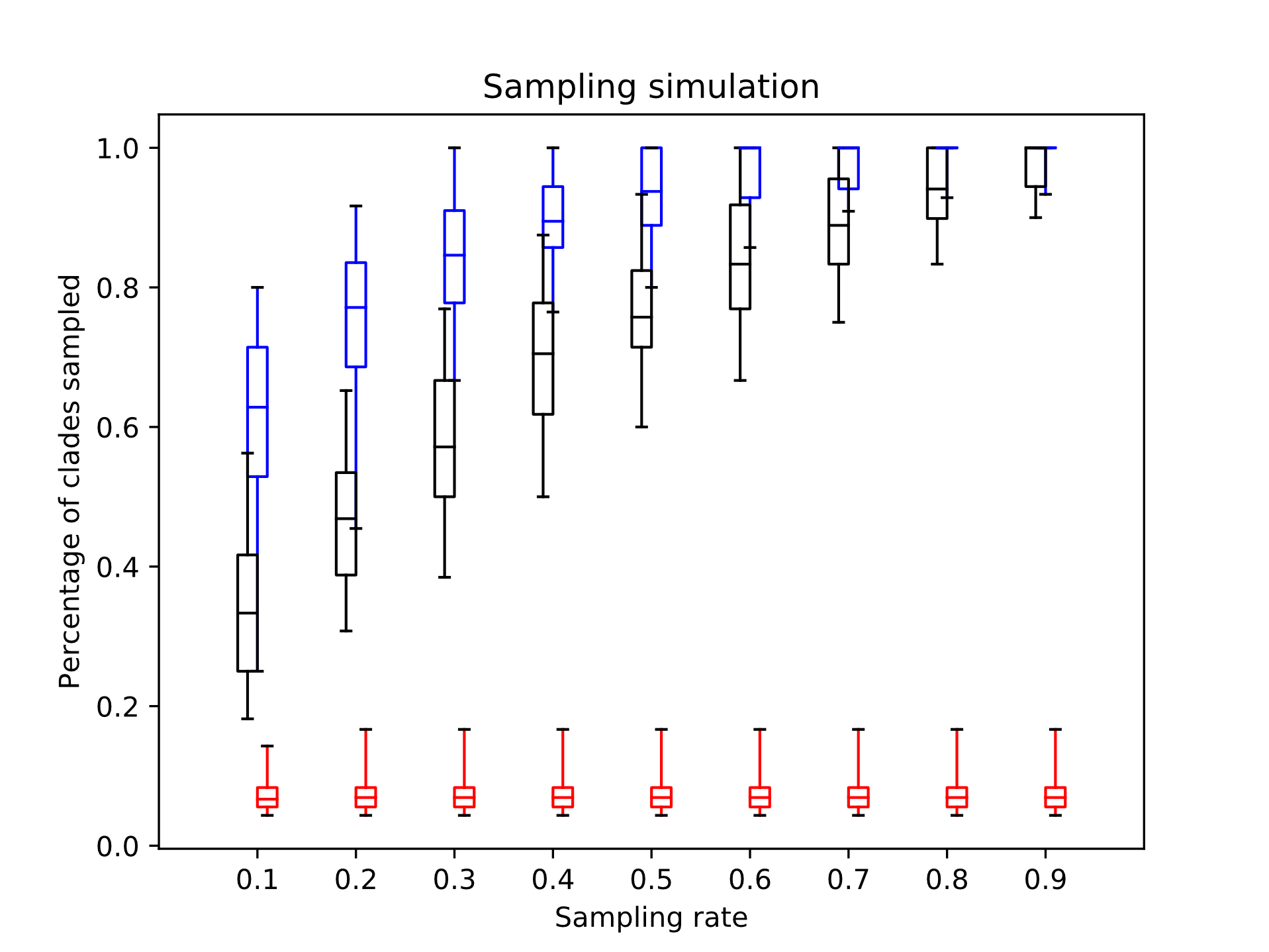
Для каждой симуляции создавалось дерево размером примерно в десяток-другой клад (нормальное распределение со средним 15 и стандартным отклонением 5) разного размера, от единиц до сотен последовательностей каждая. Согласно этому дереву генерировались случайные последовательности нуклеотидов, а затем из сгенерированного набора брались выборки от 10% до 90% последовательностей. Эффективность оценивалась как доля клад, представленных в уменьшенной выборке хотя бы одной последовательностью. Как видно, при выборе небольшого количества последовательностей DJ значительно эффективнее двух других методов.
Кстати, а что это за чудовищно неэффективный и очевидно бессмысленный выбор n последовательностей, ближайших к какой-то одной? Это, конечно, не метод уменьшения выборок, это возможный артефакт. Грубо говоря, запрос к биологической базе данных можно сформулировать либо как “дай мне 100 последовательностей, наиболее похожих на вот эту”, либо как “дай мне все последовательности, похожие на вот эту как минимум вот на столько”. Первая формулировка полезна для других задач (и чаще всего по дефолту стоит именно она), но в случае филогенетического анализа может привести к серьёзным перекосам в наборе данных.
На реальных данных в тестирование можно включить и основанный на таксономии метод AST. Ниже показаны результаты на двух набора данных: слева большой набор рибосомных РНК. Это классический маркерный ген, наследуемый практически безо всяких дупликаций или делеций и поэтому широко используемый для исследования эволюции видов. Справа набор хитинсинтаз из дерева выше.

Результат довольно предсказуем: в случае рРНК таксономические метаданные идеально описывают эволюцию и поэтому AST сильно обходит остальные методы. А вот с хитинсинтазами он не справляется по описанным выше причинам. Горизонтальная прямая сверху – это не рамка вокруг графика, это DJ охватывает все клады даже при уменьшении набора данных в пять раз.
Заключение
Строго говоря, в описанном алгоритме нет ничего специфически биологического. Да, в данном случае я использовал последовательности и биологические метрики дистанции между ними. Но тем же образом можно брать выборки из совокупностей любых объектов, для которых существует матрица дистанций и разнообразие которых нужно охватить выборкой достаточно равномерно.
Нужно только иметь в виду, что Distant Joining никак не борется с выбросами (которые он воспринимает как значимое разнообразие и включает в выборку одними из первых) и не сохраняет соотношение размеров кластеров.
Прототип на Python 3 доступен на гитхабе. Если он вдруг кому пригодится в научной работе – пожалуйста, цитируйте вот эту статью.
Автор: Алексей Морозов



