Хеш-функция—преобразование текста произвольной длинны в текст фиксированной длинны.
H=hash(P);
P—пароль ( открытый текст), длинна P от 0 до бесконечности;
H—хеш-значение (хешированный текст), длинна H=N бит (при условии что функция hash возвращает хеш-значение длинной N бит).
Хеш-функция используется в любом алгоритме шифрования. Ее функция заключается в следующем—при вводе пользователем пароля произвольной длинны, хеш-функция преобразует этот пароль в хеш-значение фиксированной длинны (ключ).
Для любого итерационного (циклического) алгоритма возможно повысить криптостойкость.
Общую схему итерационного алгоритма можно представить следующим образом представленным на Рис. 1.
Ключи находятся по следующему алгоритму:
K1=hash(PASSWORD)
K2=f(K1)
……………
Kn=f(Kn-1)
Функция f—функция преобразования ключа.
Если знать K1, то возможно вычислить все остальные Ki, i=2..n.
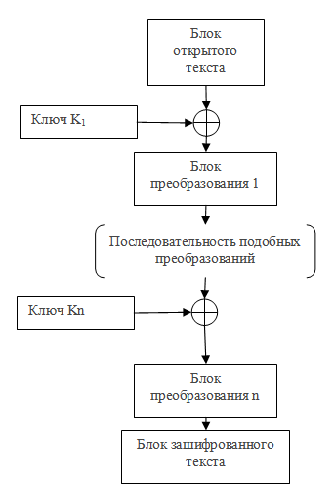
Рис. 1.—Обобщенная схема итерационных криптоалгоритмов
Злоумышленник (взломщик) не зная пароля, но зная значение хеш функции может расшифровать весь текст. Для подбора пароля методом грубой силы необходимо сделать перебор 2S значений (S—размер хеш-значения в битах). Если хеш-функция возвращает значение длинной 64 бита—потребуется сделать перебор 264 = 1.84467441×1019 значений.
Компьютер злоумышленника может перебирать 1000000 паролей в секунду. Тогда подбор хеш-значения максимально займет 213 503 982 дней.
Если использовать «атаку дней рождения» то количество вариантов сократится в среднем вдвое—264/2 = 232 = 4 294 967 296 значений. На перебор этих значений уйдет всего лишь 1.19 часов.
Методы повышения криптографической стойкости.
Метод «изменение процедуры генерации ключей»
Проведем анализ наиболее распространенных хеш-функций.
Для пароля «Password» были получены следующие хеш-значения:
| № | Хеш-функция | Хеш-значение |
|---|---|---|
| 1 | MD2 | 9dc7dd5f9b5f681a133e64c0089330e7 |
| 2 | MD4 | f15abd57801840f3348ddccafb677f6a |
| 3 | MD5 | dc647eb65e6711e155375218212b3964 |
| 4 | SHA-1 | 8be3c943b1609fffbfc51aad666d0a04adf83c9d |
| 5 | SHA-224 | a1308b7983fef7def9ffd06bed7ff767fa4216baf9d9d911af1e7e2e |
| 6 | SHA-256 | e7cf3ef4f17c3999a94f2c6f612e8a888e5b1026878e4e19398b23bd38ec221a |
| 7 | SHA-384 | d3a1ad34a5f0d265d8c0441d85532a95d02fcca0450646c21f1585cfc521843cd423d02f53e9205390706cc15f3a06fe |
| 8 | SHA-512 | e6c83b282aeb2e022844595721cc00bbda47cb24537c1779f9bb84f04039e1676e6ba8573e588da1052510e3aa0a32a9e55879ae22b0c2d62136fc0a3e85f8bb |
| 9 | Tiger-128 | 78db95bcce175ab632095962774965d1 |
| 10 | Tiger-160 | 78db95bcce175ab632095962774965d1151e1f17 |
| 11 | Tiger-192 | 78db95bcce175ab632095962774965d1151e1f1727c63f3d |
| 12 | Whirlpool | fd07ba63996cdcfa6130ee82acec65da7487f51564bb7c6ead6dabc6b9e8eac974e5d852edc545804ae68fa46fc59d4789acab50bbc22b26fb24412f8dc11cde |
| 13 | DES(Unix) | Q37hnXsCsGjCU |
| 14 | CRC-32 | 9abfd710 |
(Таблица была получена с сайта InsidePro )
Алгоритмы CRC-32, DES(Unix) использовать не желательно, т.к. они генерируют очень короткий хеш. А алгоритмы серии Tiger генерируют одинаковые хеши в начале последовательности. Об алгоритмах MD2 и MD4 были заявления о взломе.
Из претендентов на реальное использование можно рассматривать только алгоритмы серии SHA, MD5 и Whirlpool.
Наиболее оптимально использовать SHA-512 и Whirlpool.
Предположим что алгоритм шифрования требует ключ длины 64 бита.
Ключ Ks вычисленный по алгоритму SHA-512 занимает 512 бит. Разбиваем ключ на 8 подключей равной длинны. Обозначим их как Ks1, Ks2, …., Ks8.
| Ks1 | Ks2 | Ks3 | Ks4 |
| e6c83b282aeb2e02 | 2844595721cc00bb | da47cb24537c1779 | f9bb84f04039e167 |
| Ks5 | Ks6 | Ks7 | Ks8 |
| 6e6ba8573e588da1 | 052510e3aa0a32a9 | e55879ae22b0c2d6 | 2136fc0a3e85f8bb |
Аналогично поступим и с ключом Kw (хеш Whirlpool).
Получим 16 подключей Ks1 —Ks8 и Kw1 —Kw8.
Исходя из предположения что в алгоритме рассмотренном на Рис.1 n=8, возможно итерационную последовательность ключей Ki (i=1..8) заменить независимыми (не итерационными) ключами Kxi (i=1..8).
| Ключ | Значение |
|---|---|
| Kx1 | Ks1 XOR Kw5 |
| Kx2 | Ks3 XOR Kw2 |
| Kx3 | Ks5 XOR Kw3 |
| Kx4 | Ks8 XOR Kw1 |
| Kx5 | Ks4 XOR Kw7 |
| Kx6 | Ks7 XOR Kw4 |
| Kx7 | Ks6 XOR Kw8 |
| Kx8 | Ks2 XOR Kw6 |
Тогда злоумышленнику вместо 264 или 232 вариантов придется вычислять 2 хеш-функции, сложность каждой из которых 2512. И того ему придется перебрать:
1. методом «грубой силы»—1.8 × 10308 вариантов.
2. атакой «дней рождений»— 1.34 × 10154 вариантов.
Метод «изменения хеш-функции».
На основе этой статьи.
Различие в пользователе (знающим пароль) и взломщике (не знающим пароль) в количестве запуска процесса расшифрования. Пользователь запускает процесс расшифровки один раз с правильным паролем. Злоумышленник же запускает этот процесс огромное количество раз в попытке подобрать пароль.
Исходя из этой предпосылки возможно повысить криптостойкость алгоритма. Необходимо замедлить работу хеш-функции для замедления подбора пароля и осуществления анализа криптоалгоритма.
Если для создания ключа функция hash работает 1 мс. И при подборе пароля осуществляется вызов этой функции 1000 раз в секунду, то перебор 106 значений займет 1000 секунд (примерно 16 минут).
Модифицируем функцию hash таким образом что она будет работать 100 мс. Назовем получившуюся функцию slow_hash. При использовании функции slow_hash вместо hash перебор займет 100000 секунд или 27 часов.
Для пользователя замедление процесса хеширования будет практически не заметна, а взлом будет занимать на порядок больше времени.
В статье рассмотрены методы применения хеш функций в современных симметричных криптоалгоритмах.
Предложены оригинальные методы повышения криптостойкости алгоритмов к методам пассивного взлома.
Автор: karazhanov






