Не так давно вступил в силу Федеральный закон №353, обязывающий финансовые организации раскрывать информацию о так называемой «Полной стоимости кредита(займа)» (далее — ПСК).
В этой статье (в принципе относящейся только к трудящимся в финансовой сфере), я бы хотел привести пример расчета ПСК. Возможно, кому-то пригодится.
Важно! Не так давно законодатели внести изменения в формулу, которая вступает в силу только с 1 сентября 2014. Все изложенное далее пригодно только для новой формулы. Статья описывает исключительно техническую реализацию расчета ПСК в соответствии с нормами закона.
Еще важнее! Вся приведенная ниже информация актуальна для случая, когда кредит выдается ОДНИМ платежом, т.е. заемщик получает денежные средства один раз, а возвраты происходят по заранее определенному графику платежей. Такой вариант покрывает 99% выдаваемых кредитов (кредитные карты не в счет).

Понимаем значения терминов
ПСК определяется как произведение 3 величин – i, ЧБП и числа 100. Разберем используемые термины и обозначения:
-
Что такое БП (базовый период)
БП по договору потребительского кредита (займа) — стандартный временной интервал, который встречается с наибольшей частотой в графике платежей по договору потребительского кредита (займа). Если в графике платежей по договору потребительского кредита (займа) отсутствуют временные интервалы между платежами продолжительностью менее одного года или равные одному году, то БП – один год.
Фактически БП – это наиболее часто встречающийся временной интервал между платежами. Что делать, если существует 2 временных интервала которые встречаются одинаковое количество раз – в законе не уточняется.И что делать?Раз не уточняется – выбирайте любой! Но по хорошему — требуется консультация от юристов. -
Что такое ЧБП (число базовых периодов в календарном году)
Определение в законе весьма размытое, но как я понимаю – это количество базовых периодов, которые «влезают» в один календарный год, т.е.:
- Для стандартного графика платежей с ежемесячными выплатами: ЧБП = 12 (тут есть исключение – если займ выдается 31 января на 1 месяц; тогда ЧБП=13, т.к. в 365 дней «влезает» 13 периодов по 28 дней)
- Ежеквартальные выплаты: ЧБП=4
- Выплаты раз в год или реже: ЧБП=1
- Если график платежей хитрый: например предусмотрено сначала 2 выплаты раз в квартал, а затем 6 выплат раз в месяц, затем 3 выплаты раз в день, то базовый период – 1 месяц. А ЧБП=12 (12 БП за календарный год).
-
Что такое i (процентная ставка базового периода, выраженная в десятичной форме)
Это невозможно понять (по крайней мере мне). Возможно, в определении числа i есть какой-то смысл, но этот смысл уловить интуитивно не представляется возможным. Как считать i — разберем в следующем разделе.
Как считать i
Оставим на потом попытки понять «физический» смысл числа i, и дадим ему такое определение:
Число i вычисляется путем решения следующего уравнения:
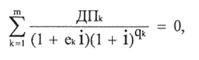 где:
где:
- m – количество денежных потоков, что равно количеству платежей в графике платежей плюс один (еще один платеж возникает из-за первого платежа – выдачи кредита).
- ДПк – размер к-го денежного потока (выдача кредита со знаком «минус», возвраты со знаком «плюс»).
- Qк — количество полных базовых периодов с момента выдачи кредита до k-го денежного потока. Qк можно вычислить по формуле:
Qк=floor[ (ДПк-ДП1)/БП ], где- ДПк – дата к-го денежного потока,
- ДП1 – дата первого денежного потока (т.е. дата выдачи),
- БП – срок базового периода,
- floor[ ] – округление вниз до целого.
- Eк — здесь сразу напишем формулу, чтобы ваш не взорвался от формулировки в законе:
Ek=mod[ (ДПк-ДП1) /БП ]/БП, где mod – остаток от деления
Алгоритм расчета ПСК
Входящие данные: два массива. Ключ – номер денежного потока, значения – даты платежа и сумма платежа.
Исходящие данные: значение ПСК (число).
Порядок расчета:
- Вычисляем ЧБП(число базовых периодов). Его вычисление с учетом всех трудностей описания в законе заслуживает отдельной статьи, поэтому здесь я не буду вдаваться в подробное описание алгоритма расчета. Но в общем суть такая: базовый период – наиболее часто встречающийся срок в днях между платежами. Число базовых периодов – сколько таких периодов «влезет» в 365 дней, т.е. ЧБП=floor[ 365/БП ].
- Для каждого k-го платежа считаем ДПk, Qk, Ek.
- Методами приближенного вычисления в точности до двух знаков после запятой считаем i.
- Умножаем ЧБП*i*100.
Код!
Есть готовое решение на javascript, а также на VBA (будет даже excel-файл для расчетов).
В примерах взят график для кредита в 100 000 рублей на 3 месяца по ставке 12% годовых. Дата выдачи — 1 сентября 2014:
| Ключ | Дата денежного потока | Сумма денежного потока |
| 0 | 01.09.2014 | -100 000 |
| 1 | 01.10.2014 | 34 002,21 |
| 2 | 01.11.2014 | 34 002,21 |
| 3 | 01.12.2014 | 34 002,21 |
Решение на javascript
function psk(){
//входящие данные - даты платежей
var dates = [
new Date(2014, 8, 01),
new Date(2014, 9, 01),
new Date(2014, 10, 01),
new Date(2014, 11, 01)
];
//входящие данные - суммы платежей
var sum = [
-100000,
34002.21,
34002.21,
34002.21,
];
var m=dates.length; // число платежей
//Считаем базовый период bp. Для этого расчитываем наиболее часто встречающийся период в днях
var days_diff=[];
for (k=1;k<m;k++){
days_diff[k]=(dates[k]-dates[k-1])/(24*60*60*1000);
}
var z=-1;
var count=[];
var i_count=[];
for (var key in days_diff) {
z++;
var val = days_diff [key];
i_count[z]=val;
count[z]=0;
for (k=1; k<m; k++){
if (days_diff[k]==val){
count[z]++;
}
}
}
var count_max=0;
var count_max_i=0;
for (j=0; j<z; j++){
if(count[j]>count_max){
count_max=count[j];
count_max_i=j;
}
}
var bp=i_count[count_max_i];
//Считаем число базовых периодов в году:
var cbp=Math.floor(365/bp);
//заполним массив с количеством дней с даты выдачи до даты к-го платежа
var days=[];
for (k=0;k<m;k++){
days[k]=(dates[k]-dates[0])/(24*60*60*1000);
}
//посчитаем Ек и Qк для каждого платежа
var e=[];
var q=[];
for (k=0;k<m;k++){
console.log("days - "+k+"="+days[k])
e[k]=(days[k]%bp)/bp;
console.log("e - "+k+"="+e[k])
q[k]=Math.floor(days[k]/bp);
console.log("q - "+k+"="+q[k])
}
//Втупую методом перебора начиная с 0 ищем i до максимального приблежения с шагом s
var i=0;
var x=1;
var x_m=0;
var s=0.00001;
while(x>0){
x_m=x;
x=0;
for(k=0;k<m;k++){
x=x+sum[k]/((1+e[k]*i)*Math.pow(1+i, q[k]));
}
i=i+s;
}
if(x>x_m){
i=i-s;
}
//считаем ПСК
var psk=Math.floor(i*cbp*100*1000)/1000;
//выводим ПСК
alert("ПСК = "+psk+" %");
}
Демо на jsfiddle: jsfiddle.net/exmmo/m5kbb0up/1/
Решение на VBA+excel
В столбце B, начиная с 2ой строки находятся суммы денежных потоков.
Sub psk()
Dim dates()
Columns("A:A").Select
dates() = Application.Transpose(Range(ActiveCell, Cells(Rows.count, ActiveCell.Column).End(xlUp)))
Dim summa()
Columns("B:B").Select
summa = Application.Transpose(Range(ActiveCell, Cells(Rows.count, ActiveCell.Column).End(xlUp)))
Dim m As Integer
m = UBound(dates)
ReDim days_diff(m)
For k = 3 To m
days_diff(k) = dates(k) - dates(k - 1)
Next
Z = 2
ReDim count(m)
ReDim i_count(m)
For Key = 3 To m
Z = Z + 1
V = days_diff(Key)
i_count(Z) = V
count(Z) = 0
For k = 3 To m
If days_diff(k) = V Then
count(Z) = count(Z) + 1
End If
Next
Next
count_max = 0
count_max_i = 0
For j = 2 To m
If count(j) > count_max Then
count_max = count(j)
count_max_i = j
End If
Next
bp = i_count(count_max_i)
cbp = 365 bp
ReDim Days(m)
For k = 2 To m
Days(k) = dates(k) - dates(2)
Next
ReDim e(m)
ReDim q(m)
For k = 2 To m
e(k) = (Days(k) Mod bp) / bp
q(k) = Days(k) bp
Next
i = 0
x = 1
x_m = 0
s = 0.000001
Do While x > 0
x_m = x
x = 0
For k = 2 To m
x = x + summa(k) / ((1 + e(k) * i) * ((1 + i) ^ q(k)))
Next
i = i + s
Loop
If x > x_m Then
i = i - s
End If
psk = Round(i * cbp, 5)
Cells(3, 7).Value = psk
End Sub
Демо в Excel+VBA: yadi.sk/i/nRce6jnqa6CcR
Заключение
Код далек от совершенства, можно даже сказать, что он убогий. Например, приближенное вычисление выполняется самым глупым из известных человечеству способом. Прошу понять и простить, в текущей ситуации времени на написание чего-то презентабельного категорически не хватает. Виноват, исправлюсь.
Если у вас есть замечания или вы нашли ошибку — прошу сообщать, буду благодарен. Самое опасное, что может быть — изначально неверная трактовка текста закона.
Автор: exmmo