При расчетах в технике высоких частот с применением зеркальных отражающих систем (параболических зеркал) всегда возникает задача поиска фазового центра антенны (ФЦА), т.к. правильная работа зеркала возможна только, если в фокусе находится антенна (именуемая облучатель, feeder, feedhorn) которая имеет фазовый фронт волны в виде сферы, и центр этой сферы находится в фокусе зеркала. При любых отклонениях, как формы фазового фронта от сферы, так и смещения ФЦА из фокуса зеркала — КПД зеркальной системы падает, потому что искажается её диаграмма направленности.
Хотя тема поиска ФЦА довольно актуальна даже в быту, потому что кроме традиционных антенн спутникового телевидения нашли распространение параболические антенны для WiFi, WiMAX и сотовой связи (UMTS/3G, LTE/4G) — тем не менее в литературе такая тема освещена слабо и пользователи часто путают фазовую ДН с обычной диаграммой направленности.
В видеороликах о программах компьютерной симуляции иногда можно встретить практические инструкции как искать ФЦА, но обычно там нет даже минимальных объяснений что ищем и что получаем.
Поэтому чтобы восполнить пробел, напишем небольшую статью с практическими примерами.
Фазовая диаграмма направленности – это зависимость фазы электромагнитного поля, излучаемого антенной, от угловых координат.
(А.П. Пудовкин, Ю.Н. Панасюк, А.А. Иванков — Основы теории антенн)
Так как в дальней зоне антенны векторы поля Е и Н синфазны, то и фазовая ДН в одинаковой степени относится к электрической и магнитной составляющей ЭМП, излучаемого антенной.
Обозначается фазовая ДН следующим буквой Пси:
Ψ = Ψ (θ, φ), при r = const.
Если Ψ(θ, φ) = const при r = const, то это означает, что антенна формирует фазовый фронт волны в виде сферы.
Центр этой сферы, в котором находится начало системы координат, называют фазовым центром антенны (ФЦА).
Фазовый центр антенны — это точка, в которую можно поместить одиночный излучатель сферической волны, эквивалентный рассматриваемой антенной системе в отношении фазы создаваемого поля.
(Драбкин А.Л., Зузенко В.Л. Антенно-фидерные устройства)
ФЦА имеют не все антенны. У антенн, имеющих фазовый центр и многолепестковую амплитудную ДН с чёткими нулями между ними, фаза поля в соседних лепестках отличается на π (180°).
Взаимосвязь между амплитудной и фазовой диаграммами направленности одной и той же антенны иллюстрируется
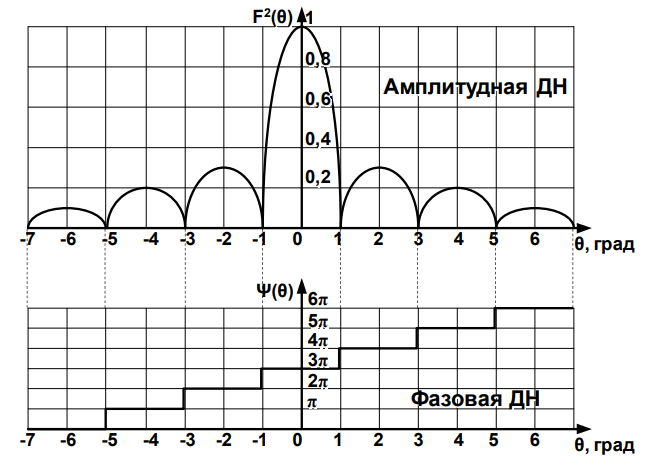
В реальных антеннах фазовый центр обычно рассматривается в рамках ограниченных углов главного лепестка диаграммы направленности. Положение фазового центра зависит от частоты используемого сигнала, направления излучения/приема антенны, его поляризации и других факторов. Некоторые антенны не имеют фазового центра в общепринятом понимании.
В простейших случаях, например у параболической антенны, фазовый центр совпадает с фокусом параболоида и может быть определен из геометрических соображений. В более сложных случаях, например, рупорных антенн, положение фазового центра не очевидно и требует соответствующих измерений.
Натурные измерения фазового центра очень трудоёмкие (особенно в широкой полосе частот).
В CAD-симуляторах электромагнитных полей вычисление ФЦА это очень простая задача, но она всё же требует несколько ручных манипуляций, т.к. выполняется она «брут-форсом» и требует небольшой начальной настройки функции, которую собираемся брутфорсить.
Для практических расчетов возьмем реальный облучатель парабол для диапазона Ku-band — LNB производителя Inverto, серия Black Ultra.
Этот фидер имеет такой вид (в разрезе)
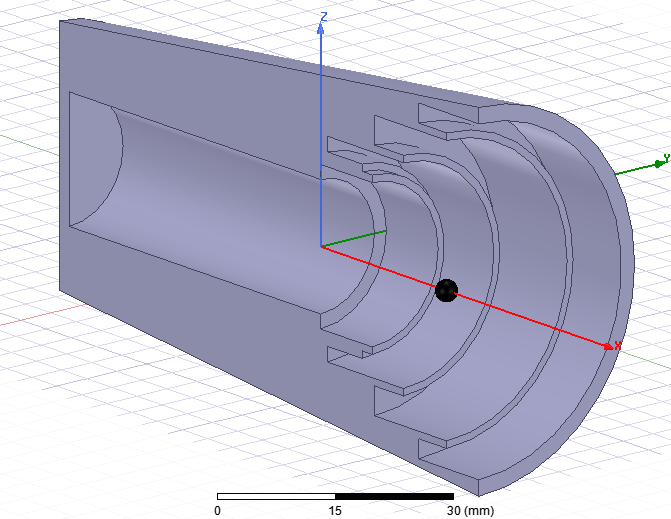
Шарик размером с горошину — это и будет ФЦА, но мы ещё этого не знаем и наша задача найти его положение.
В примере будем использовать такие вводные:
— частота расчета 11538.5 МГц (длина волны 25.982 мм)
— линейная горизонтальная поляризация (в оси Y)
— сама антенна направлена по оси X, т.е. главное направление излучения θ=90, φ=0
Расчет традиционных параметров дальнего поля (Far Field) в Ansys HFSS дает такую диаграмму направленности в 3D и 2D
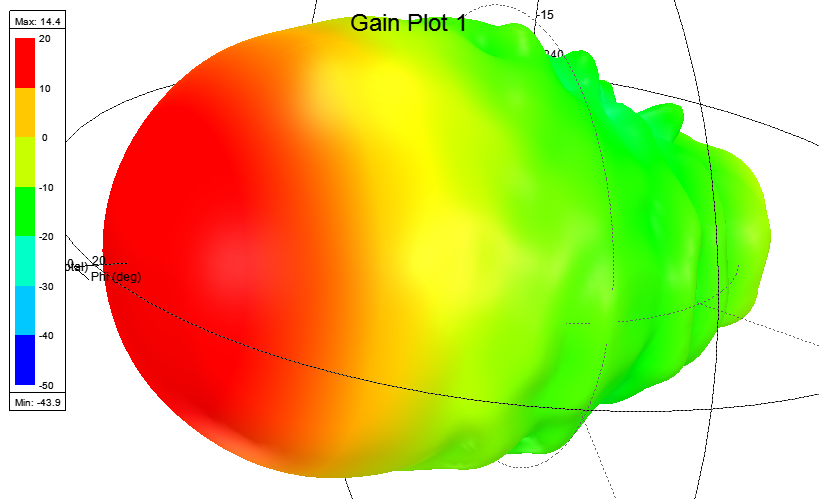
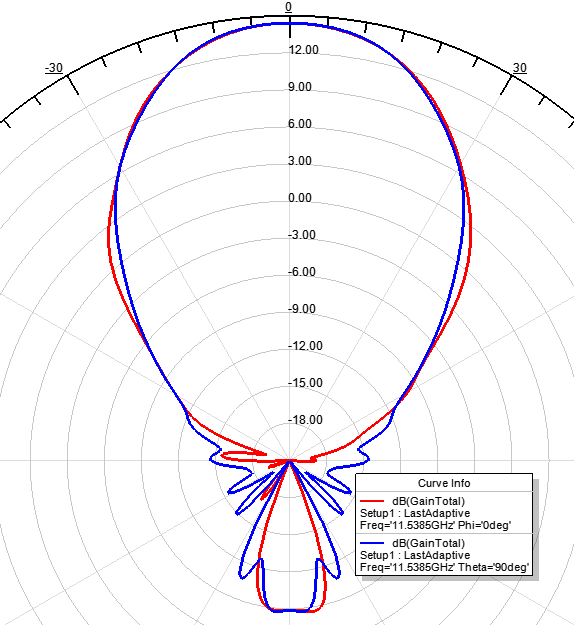
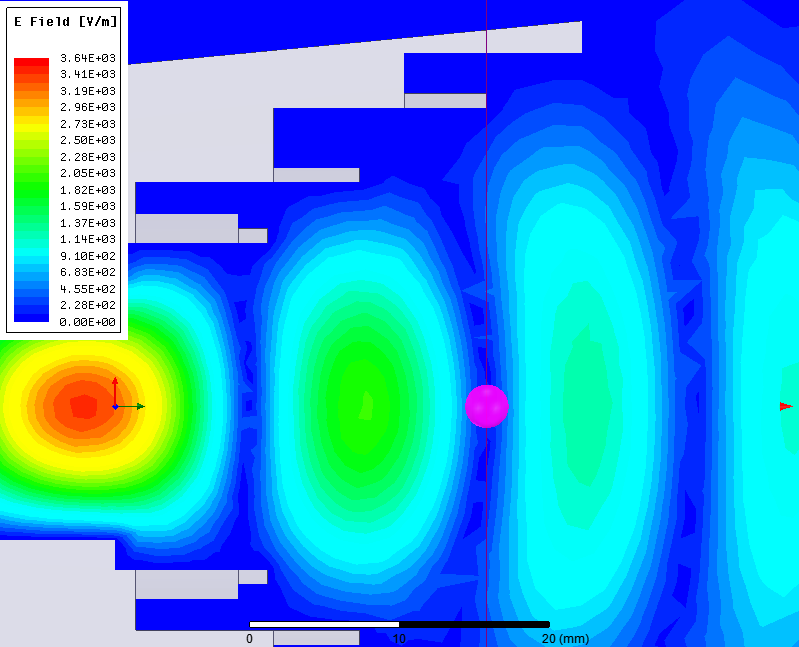
Мгновенные значения напряженности (Вольт/метр) электрического поля (E-field) в зависимости от фазы
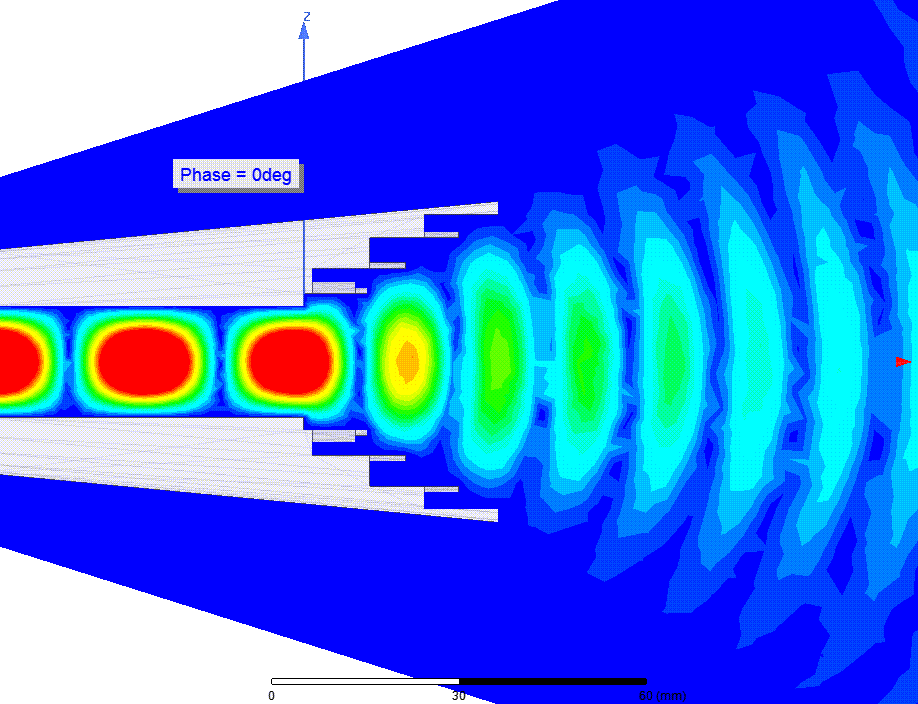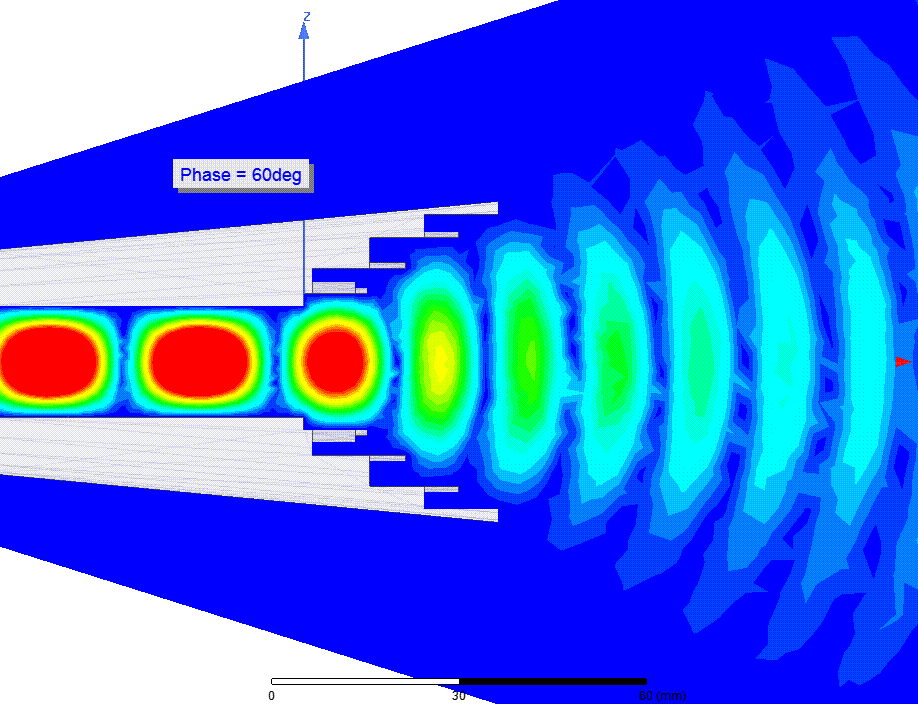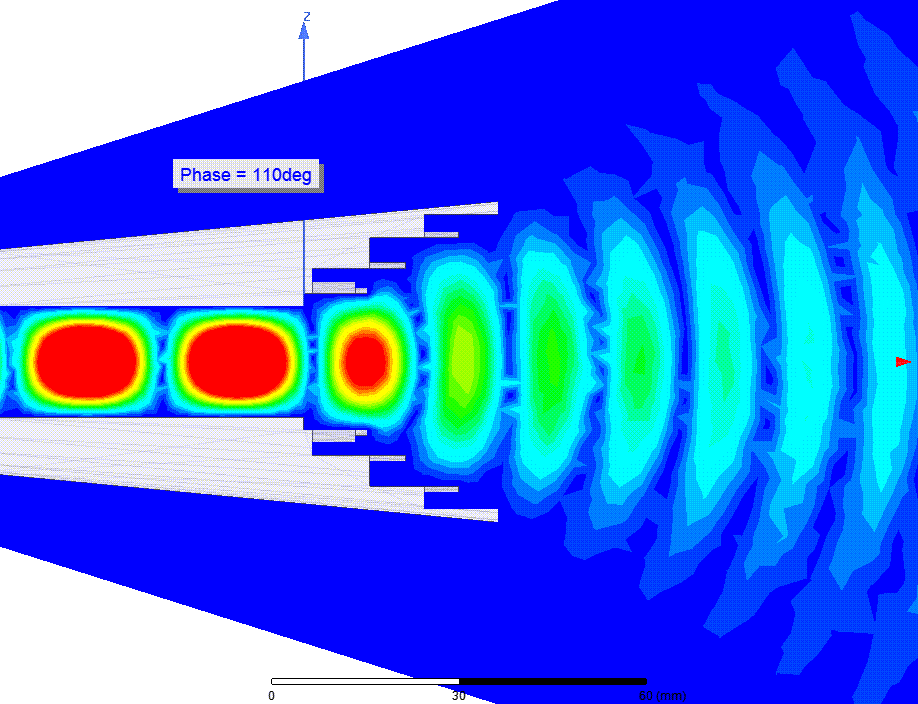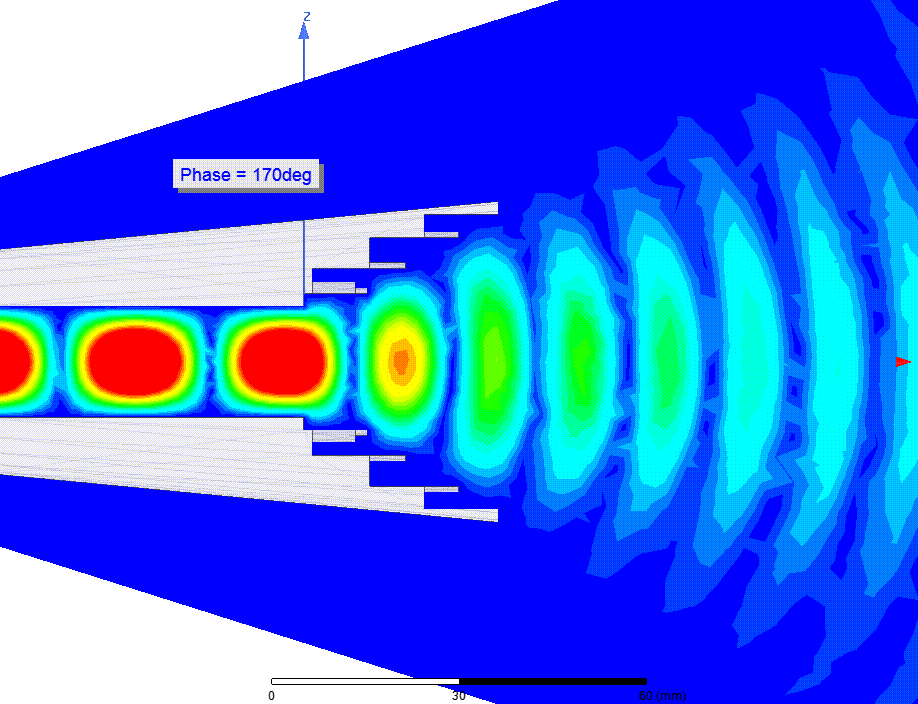
Интегральная напряженность E-поля (за >1 оборот волны)
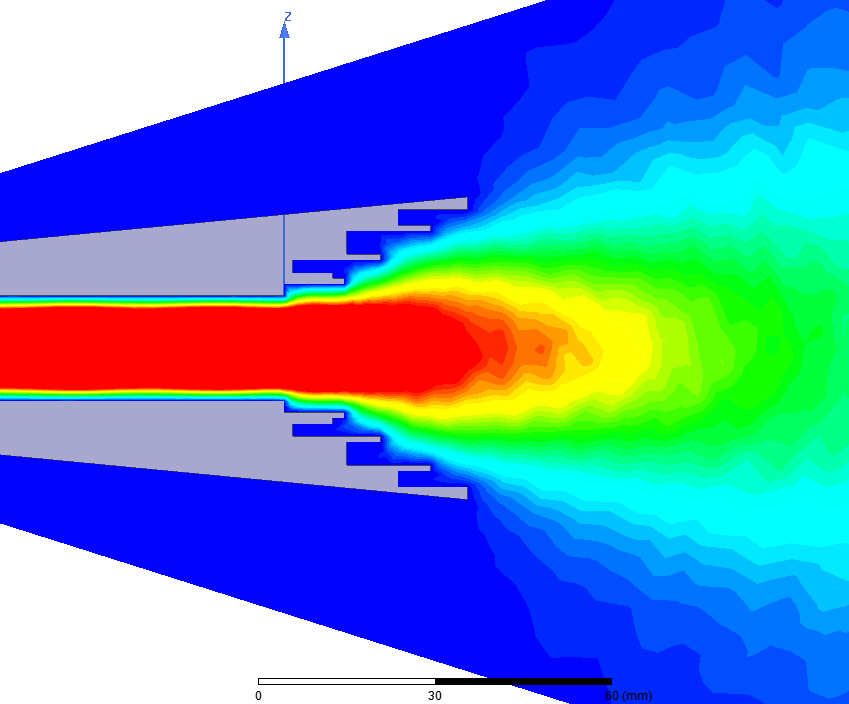
Все такие параметры дальнего поля (Far-Field) как при натурных измерениях, так и в CAD-симуляциях — рассчитывается на бесконечной сфере — Infinite Sphere. Испытуемая антенна или её компьютерная модель помещается в центр такой сферы, а измерительный зонд двигается по периметру такой сферы и измеряет амплитуду, поляризацию (амплитуду одного из компонентов) и фазу ЭМ волны. Зонд можно закрепить стационарно и поворачивать испытуемую антенну.
Главное чтобы:
— расстояние всегда было одинаковое (т.е. это была именно измерительная сфера)
— радиус сферы был достаточно большой (не менее 5-10 лямбд), чтобы измерения проводились только в той области пространства где векторы электрического поля Е и магнитного H синфазны, т.е. ни одна из компонент не преобладает и не смещена по фазе (не имеет реактивности) за счет носителей заряда которые есть в металлических проводниках антенны или за счет заряженных молекул диэлектрика.
В Ansys HFSS для проведения измерений дальнего поля необходимо создать хотя бы одну бесконечную сферу: Radiation -> Insert Far Field Setup -> Infinite Sphere
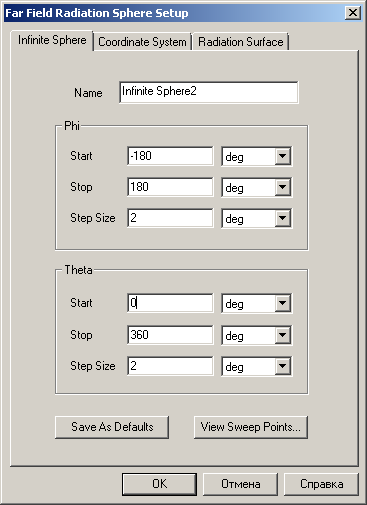
φ и θ можно всегда указывать от 0 до 360, но чтобы экономить время на вычислениях иногда рационально ограничить исследуемый угол некоторым сектором. При задании шага 1 градус, полная сфера будет занимать 360*360 = 129 600 расчетных точек, а при шаге 0.1 градус почти 13 млн. Для создания 3D/2D отчетов диаграммы направленности обычно достаточно шага 2-3 градуса (14 400 расчетных точек при шаге 3 градуса). Шаг 1 градус и менее есть смысл использовать только для анализа среза
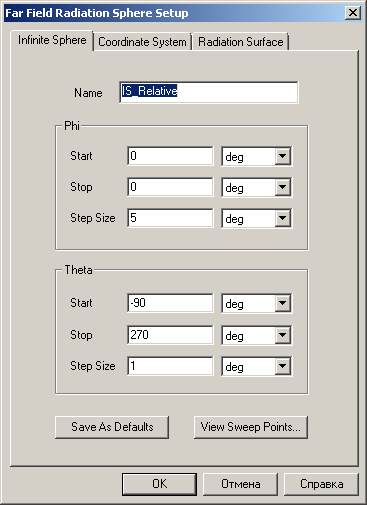
В закладке «Coordinate System» каждая сфера обязательно имеет свой центр координат. По умолчанию там всегда стоит глобальный центр координат проекта [0, 0, 0]. При желании можно добавлять любое количество других относительных координат. Как элементы геометрии модели так и пользовательскую сферу «Infinite Sphere» можно назначать относительно глобального центра координат или относительно пользовательского. Этим мы воспользуемся ниже.
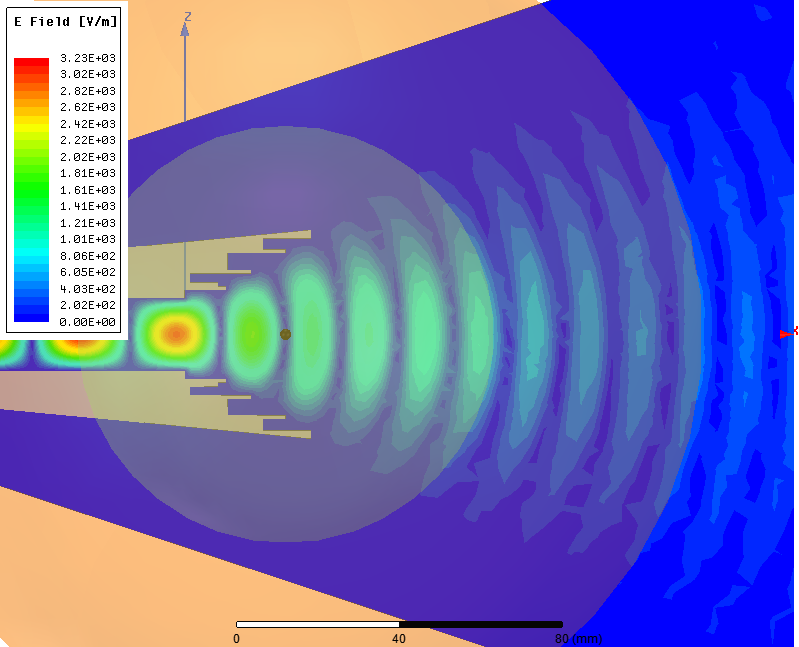
Расходящийся фазовый фронт волны было видно на анимации Е-поля выше. ЭМ волна образует концентрические круги, подобные кругам на воде от брошенного камня. Фазовый центр это точка, в которую бросили такой камень. Видно что его положение находится где-то в раструбе рупора, но точное его положение не очевидно.
Метод поиска ФЦА базируется на том, что мы смотрим на направление вектора Е-поля (его фазу) по поверхности бесконечно удаленной сферы.
Для демонстрации создадим 2 анимации с векторами Е-поля на сфере с радиусом 4 лямбда (это не бесконечная сфера, но для лучшего масштаба рисунка такого радиуса вполне достаточно).
На первой анимации центр сферы размещен точно в ФЦА

На второй анимации центр размещен в точке проекта 0, 0, 0 (забегая наперед скажем что она находится на 25.06 мм позади ФЦА)
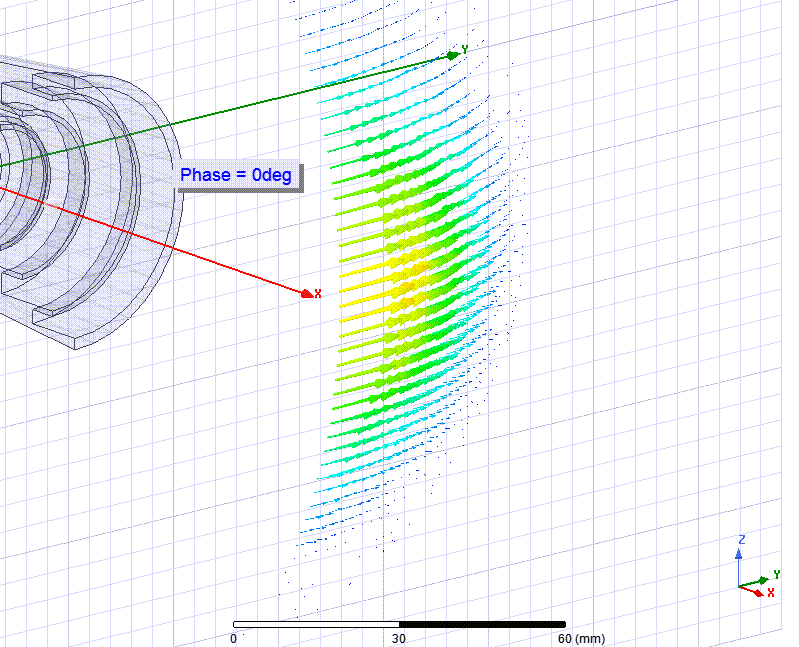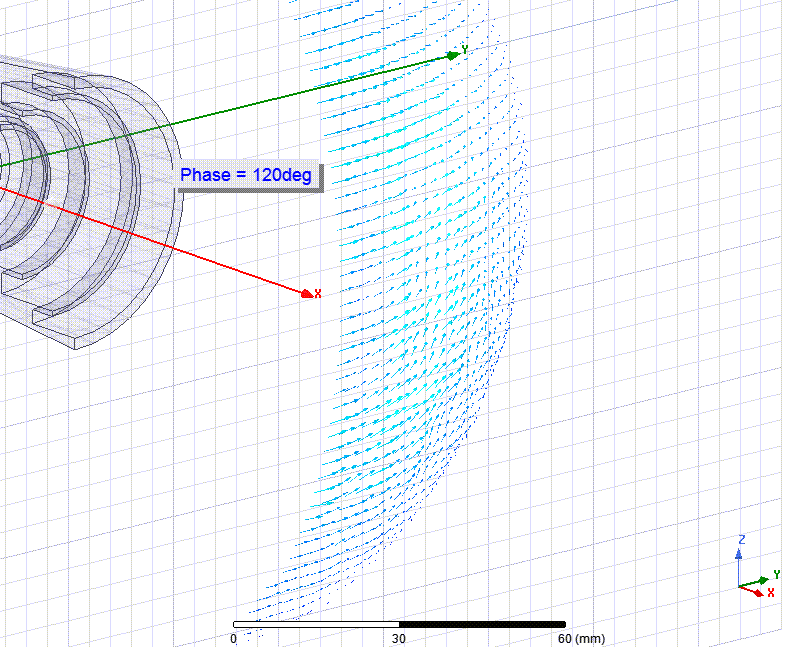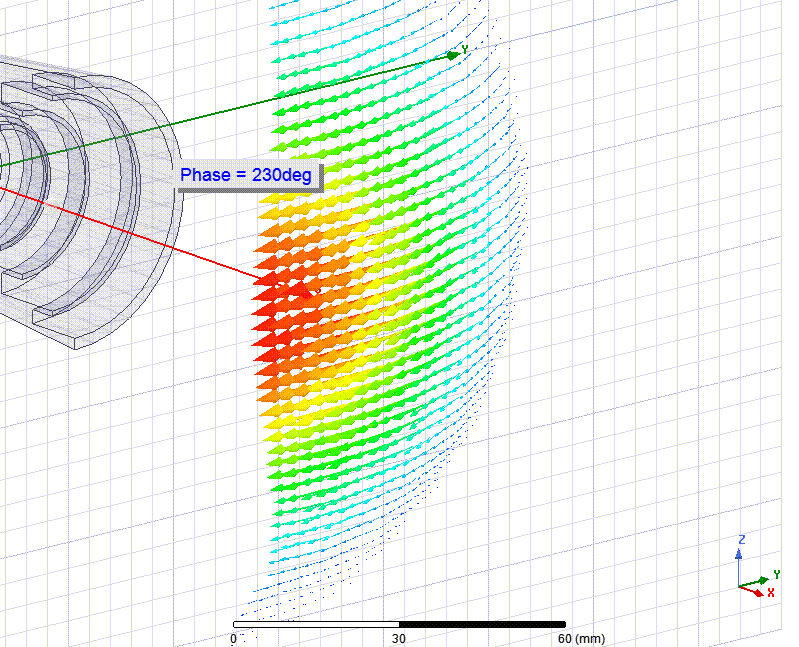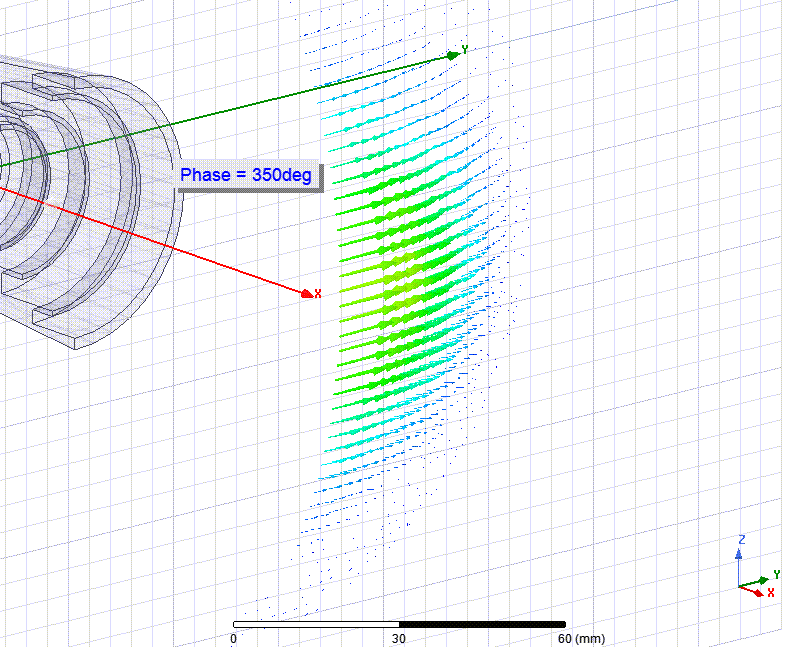
На поверхности первой сферы (она кривая, это не плоскость) видно что векторы движутся синхронно. Амплитуда (magnitude) их разная, потому что ДН антенны имеет максимум в центре (до 14.4 dBi) который плавно угасает в 2 раза (-3 dB) при углах ±20°.
Нас интересует не цвет/длина, а направление вектора. Чтобы все они двигались синхронно (синфазно).
На первой анимации все векторы двигаются синхронно, как бы мяч вращается то вправо то влево.
На второй анимации векторы несинхронны, одни уже изменили направление движения, другие ещё нет. Поверхность этой сферы постоянно претерпевает поверхностные натяжения/деформации.
Первая сфера — находится в ФЦА, вторая не находится в ФЦА.
Задача поиска ФЦА по этому методу состоит в том, чтобы с мелким шагом двигать (брутфорсить) Infinite Sphere до тех пор, пока разброс фаз на интересующем нас участке этой сферы (нас интересует только главный лепесток излучения) станет минимальным (в идеале — нулевой).
Но перед тем как перейти к брутфорсу, сначала разберемся как в HFSS можно отобразить фазовую ДН.
В отчетах дальнего поля «Results -> Create Far Field Report» мы можем вывести или традиционный прямоугольный график (Rectangular plot) или 2D круговой график (Radiation pattern) где по одной оси (например X) вывести зависимость угловой координаты (например θ), а по оси Y — значения фазы на этих углах θ.
Нужный нам отчет это rE — «излученное (radiated) E поле».
Для каждого угла [φ, θ] на бесконечной сфере рассчитывается комплексное число (вектор) электрического поля.
При построении обычных амплитудных графиков (диаграмма направленности, распределение мощности излучения по направлению) нас интересует амплитуда (mag) этого поля, которую можно получить или как mag(rE) или сразу используя более удобную переменную Gain (мощность приведена относительно мощности на порте возбуждения и относительно изотропного излучателя).
При построении фазовой ДН нас интересует мнимая часть комплексного числа (фаза вектора) в полярной нотации (в градусах). Для этого используется математическая функция ang_deg (угол_в_градусах) или cang_deg (накопленный_угол_в_градусах)
Для антенны LNA Inverto Black Ultra, фазовая ДН в плоскости XZ (φ=0) при горизонтальной поляризации возбуждения (rEY) имеет такой вид
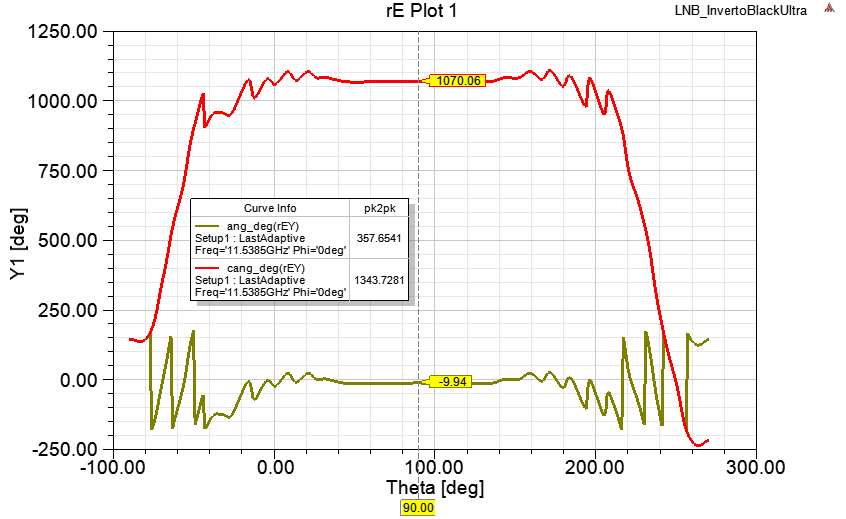
Угол Theta=90 это излучение вперёд, Theta=0 вверх, Theta=180 вниз.
Значения ang_deg изменяются от -180 до +180, угол 181° это угол -179°, поэтому график имеет форму пилы при проходе через точки ±180°.
Значения cang_deg накапливаются если направление изменения фазы постоянно. Если фаза сделала до 3 полных оборотов (6 раз пересекла 180°) то накопленное значение достигает 1070°.
Как было написано в начале статьи, фазовая и амплитудная ДН у антенн обычно связаны одна с другой. В соседних амплитудных лепестках (beam) фазы отличаются на 180°.
Наложим один на другой графики фазовой (красный/салатовый) и амплитудной (фиолетовый) ДН
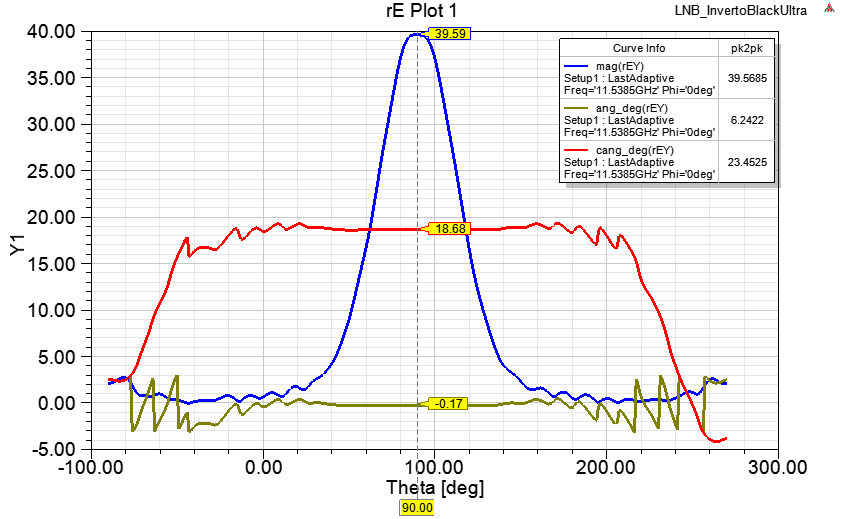
Горбы на амплитудной ДН четко следуют переломам фазы, как и написано в книгах.
Нас интересует фазовый фронт только в определенном секторе пространства, в пределах главного лепестка излучения (остальные лепестки всё равно светят мимо параболического зеркала).
Поэтому ограничим график только сектором ±45°.
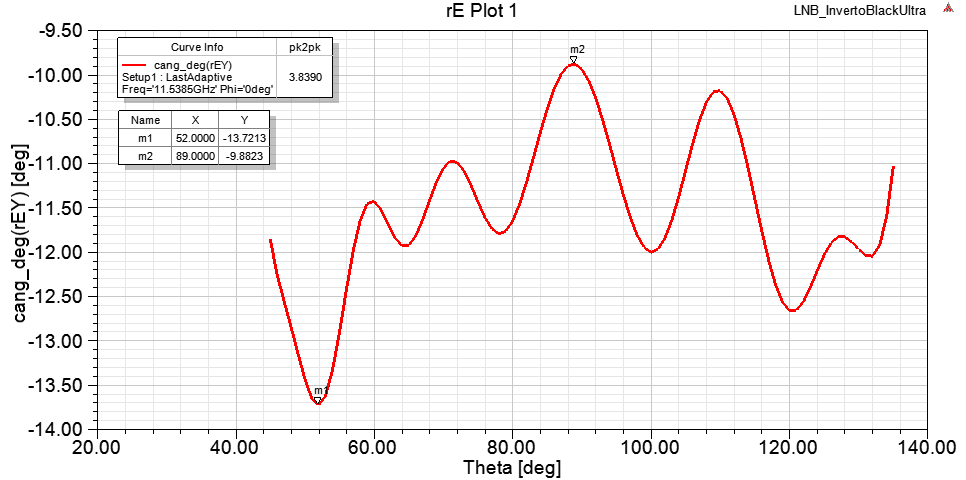
Добавим на график маркеры MIN (m1) и MAX(m2) которые показывают наибольший разброс фаз в исследуемом секторе.
Кроме того добавим математическую функцию pk2pk() которая автоматически ищет на всём графика минимум и максимум и показывает разницу.
На графике выше разница m2-m1=pk2pk= 3.839 °
Задача поиска ФЦА состоит в том, чтобы двигать с мелким шагом Infinite Sphere пока значение функции pk2pk(cang_deg(rE)) не минимизируется.
Для передвижения Infinite Sphere необходимо создать ещё одну дополнительную систему координат: Modeler -> Coordinate System -> Create -> Relative CS -> Offset
так как мы заведомо знаем, что у симметричного рупора ФЦА будет находиться на оси Х (Z=Y=0), то для Z и Y ставим 0, а двигать будет только вдоль оси X, для чего присвоим переменную Pos (с начальным значением 0 мм)
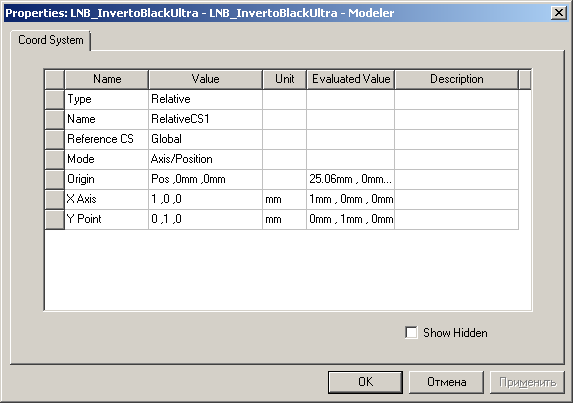
Чтобы автоматизировать процесс брут-форса, создадим задачу на оптимизацию.
Optimetrics -> Add -> Parametric, и зададим шаг переменной Pos 1 мм, в диапазоне от 0 до 100 мм
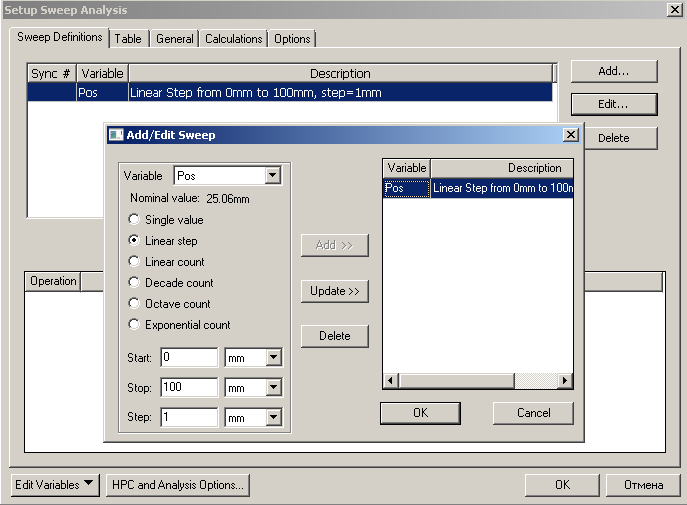
В закладке «Calculations -> Setup Calculation» выберем тип отчета «Far Field» и функцию pk2pk(cang_deg(rEY)). В кнопке «Range Functions» укажем диапазон от -45 до +45 градусов (или любой другой интересующий)
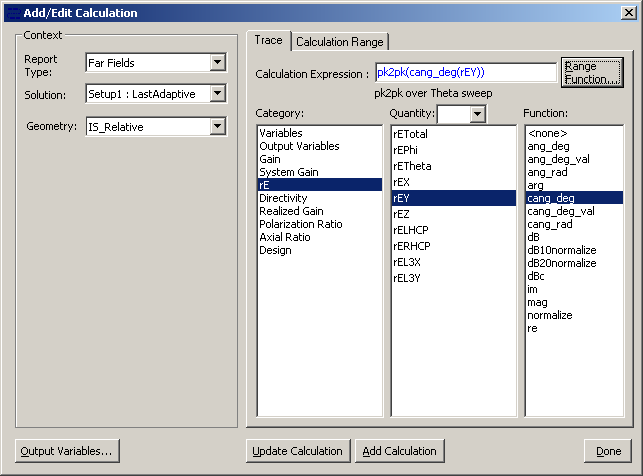
Запускаем ParametricSetup1 -> Analyze.
Расчет выполняется достаточно быстро, т.к. все расчеты дальнего поля относятся к Post-Processing и не требуют повторного решения модели.
После завершения расчета нажимаем ParametricSetup1 -> View analysis results.
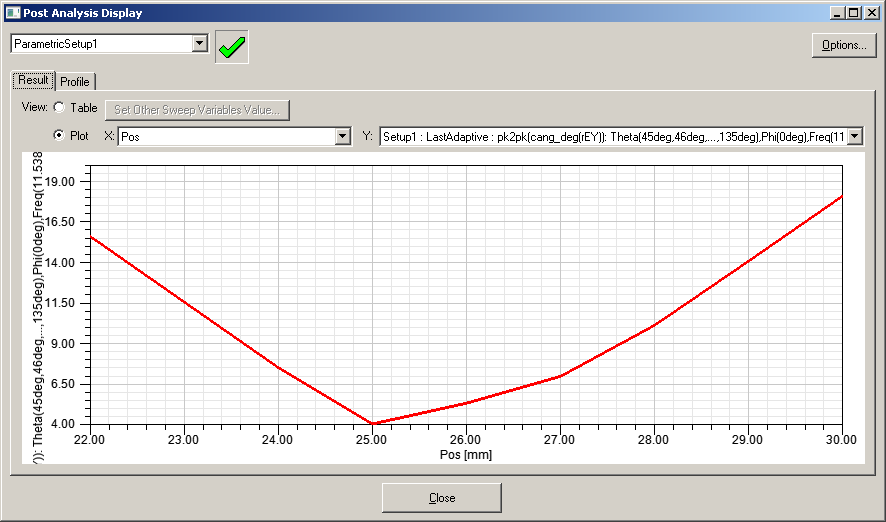
Видим четкий минимум при расстоянии X=25mm
Для более высокой точности редактируем параметрический анализ в диапазон 25.0-25.1 мм с шагом 0.01 мм
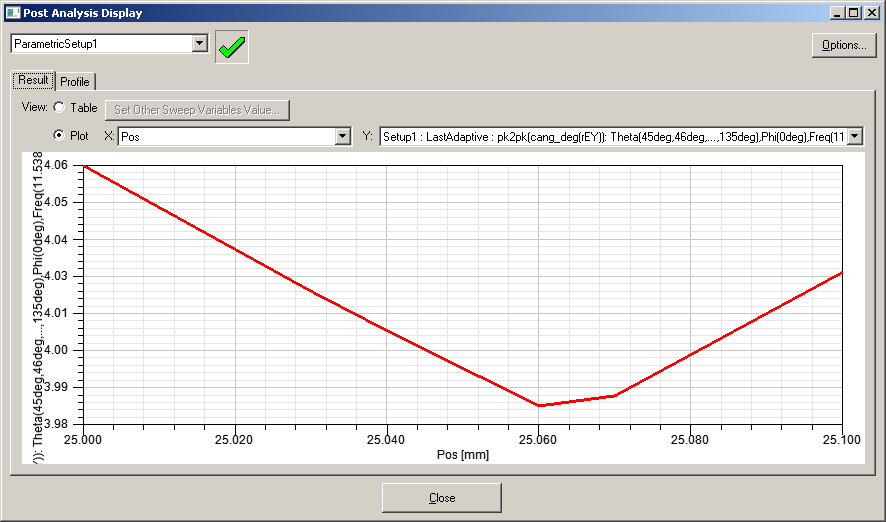
Получаем четкий минимум на X=25.06 мм
Чтобы визуально оценить где в модели получился ФЦА, можно нарисовать сферы (Non-model) или точки.
Вот в точку X=25.06 мм помещены 2 сферы (радиусом 2 и 4 лямбда)
Вот то же, в анимации
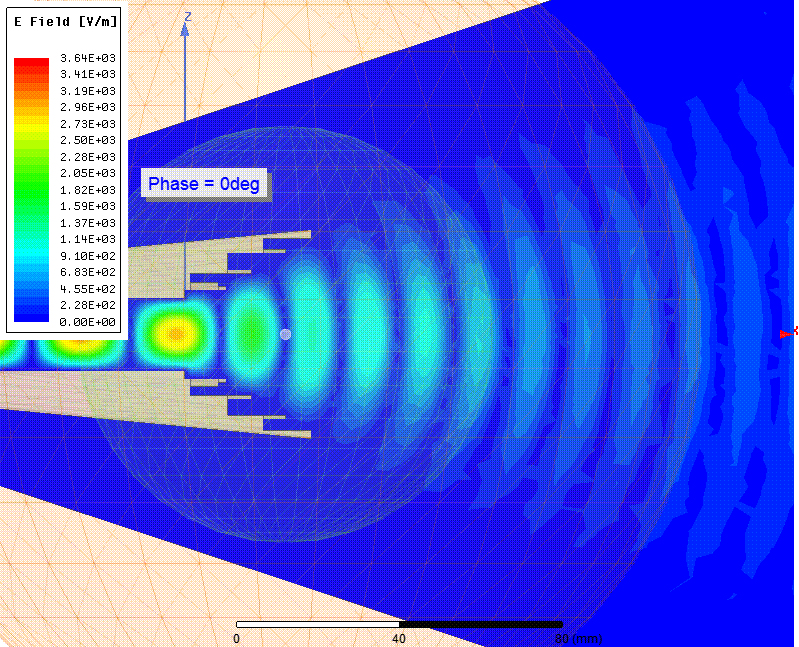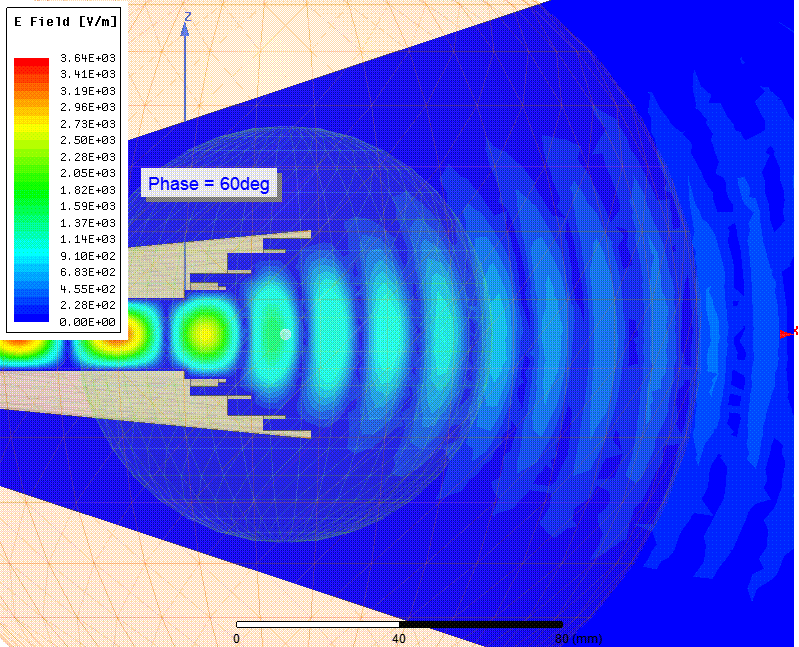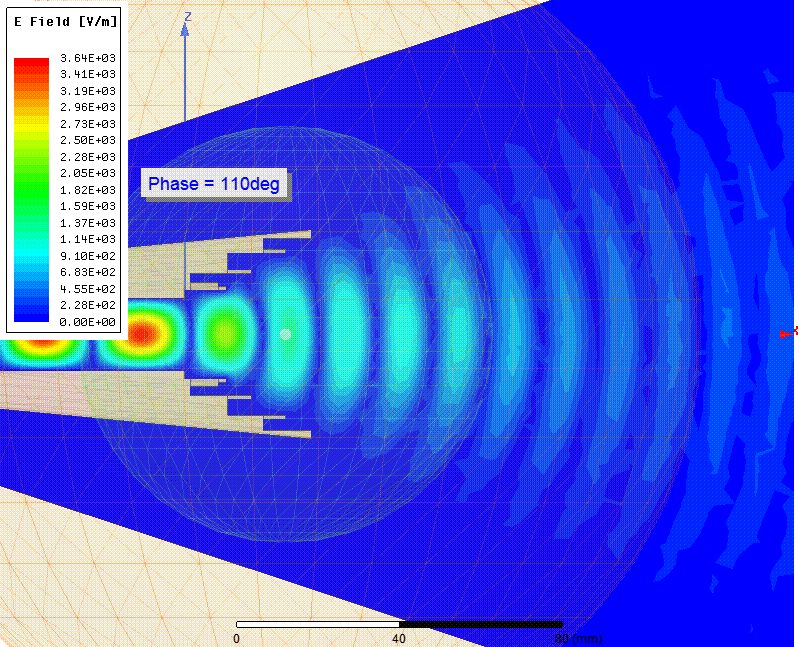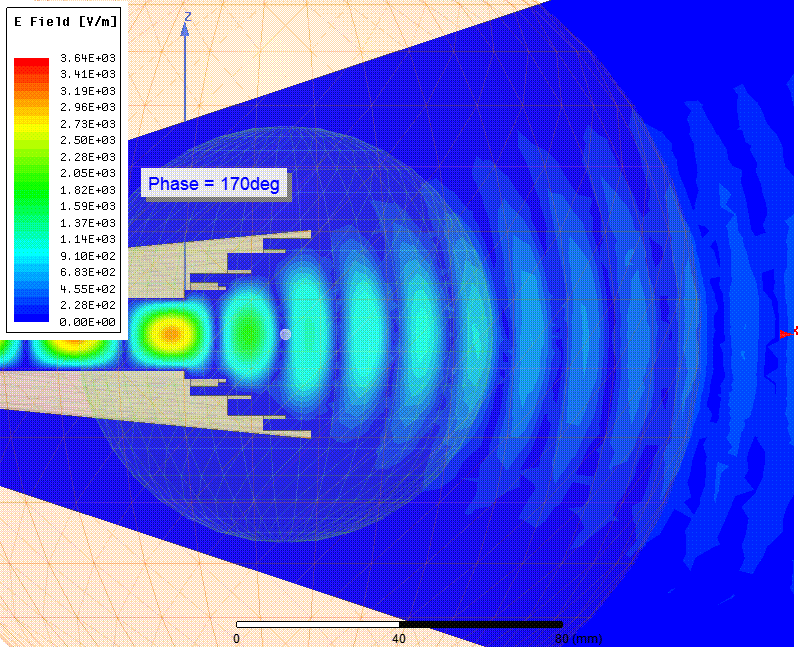
Вот более крупным планом нарисована плоскость и горошина в точке X=25.06
Широко распространено ошибочное мнение, что в HFSS (и других программах, например CST) при наложении графика «3D Plot» на геометрию антенны такой график автоматически помещается в ФЦА.
К сожалению это не так. График 3D всегда накладывается в центр координатной системы, которая были использована при задании «Infinite Sphere» для этого графика. Если использовалась глобальная система координат по умолчанию [0, 0, 0], то 3D Plot будет размещен в 0,0,0 (даже если сама антенна находится далеко в стороне).
Чтобы совместить графики, в настройках 3D Plot необходимо выбрать такую «Infinite Sphere» (создать ещё одну), для которой задана «Relative CS» в точке ФЦА которую мы нашли вручную.
Следует отметить, что такое наложение будет правдиво только для исследуемого сектора (например главного луча ДН), в боковых и задних лепестках ФЦ может находиться в другом месте или быть несферичным.
Также отметим, что настройки «Infinite Sphere» не имеют никакого отношения к граничному условию «Radiation Boundary». Слой Rad можно задавать как прямоугольник, конус, цилиндр, шар, элипсоид вращения и как угодно двигать его положение, форму и поворот. Положение и форма «Infinite Sphere» от этого никак не изменится. Это всегда будет сфера (шар) с бесконечным (достаточно большим) радиусом и с центром в заданной координатной системе.
Файл модели LNB_InvertoBlackUltra.aedt для изучения доступен по ссылке: https://goo.gl/RzuWxW (Google Drive). Для открытия файла требуется Ansys Electronics Desktop v19 или выше (не ниже 2018.1)
Автор: plyrvt






