Не всегда же только пользоваться. Именно с такой мысли началось написание библиотеки под Android и последующее написание этой статьи. Вдруг кому пригодится. Под катом то, что в итоге получилось.
Введение
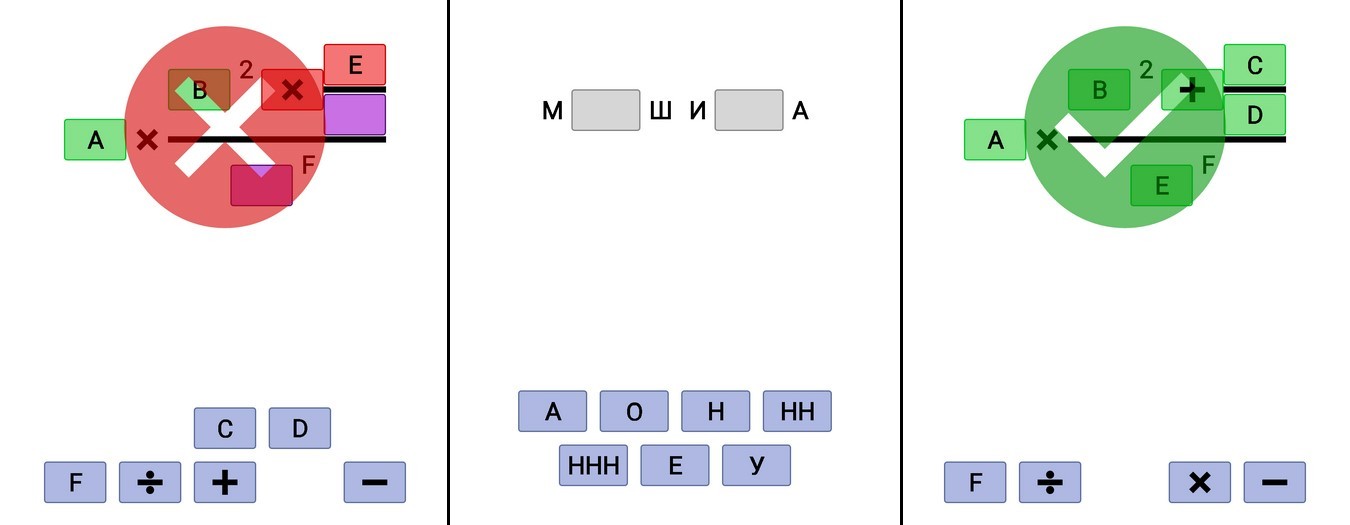
Одним долгим зимним вечером у нас с друзьями разгорелся спор, как реализовать один из необходимых функционалов. Необходимо было написать *нечто*, что смогло бы:
- Отрисовать формулу
- Отрисовать несколько блоков с буквами/цифрами
- Позволить пользователю подвигать блоки и заполнить ими пропуски в формуле.
Как самому активному, мне не терпелось испробовать силы, и в первую же ночь была написана view, которая на основе дерева формулы рисовала формулу. Посмотрели друзья на это дело и выдвинули еще требования.
- Дерево — это, конечно, хорошо, но разбираться в твоей логике заморочно, да и формулы хранить неудобно. Поэтому формула должна задаваться строкой, как формула в математике (можно добавить немного своих знаков, но все должно быть прозрачно).
- Коль такой умный, то пиши это так, чтобы внедрение в проект происходило максимально легко.
Пригорюнился добрый молодец, почесал головушку и сел писать библиотеку. А чтобы было еще интереснее, поставил я себе дополнительно условие:
- View должна быть максимально кастомизируема.
P.S.
Здесь не будет поэтапного расписывания как написать библиотеку и как ее опубликовать – в интернете, и в том числе на Хабре, уже есть инструкции на этот счет. Я немного расскажу о своей логике, о тех проблемах и сложностях, с которыми столкнулся и как их решал. Кому-то это покажется банальным, кому-то неправильным – не претендую на верное решение и все замечания учту. Надеюсь, что кому-то пригодится эта статься или библиотека. Ссылка на github будет в конце. В описании к репозиторию есть ссылка на демо библиотеки и инструкция к ней.
Этап первый – отрисовка дерева
К этому этапу у меня была моя первоначальная демка, требования и твердая уверенность, что все получится. Перво-наперво было решено взяться за отрисовку, а преобразование из строки в дерево оставить напоследок.
И так, логика дерева такова:
Лист – это набор символов. Например знак умножения или какое-то число. Лист знает о своих размерах, о том, есть ли после него кто-то, и как их расположить относительно себя. Я выделил несколько видов.
- Constable лист. Это +,-,* и числа. Этот лист имеет единичную высоту и длину в зависимости от внутреннего текста. Все, что за ним, рисуется на одной оси с ним. То есть центр этого листа по оси Y совпадает с центром по оси Y всего, что есть за ним.
- Changeable лист. Он такой же как и constable, только у него есть состояния пустой и заполненный. Высота – единичный блок. Ширина же берется не по его внутренностям, а по самому длинному тексту из всех изменяемых и перемещаемых листов.
- Movable лист. Похож на changeable, только к него состояния видим, невидим, перемещается.
- Power лист. Он имеет ширину по размеру того, что должно быть в степени. И особенность его в том, что все за ним рисует не на одной оси с предыдущим листом. Нижний край всей последующей области должен быть смещен на пол блока относительно предыдущего листа. Звучит замудрено, но надо просто приставить число в степени. (22) Степень рисуется на пол строки выше. Только в отличие от этой степени, в моей число в степени не уменьшается по шрифту. Этот лист знает о том, кто следующий в отрисовке степени, и кто следующий, после отрисовки степени. То есть в формуле (2^(1+3)-4) знак степени знает о «1» и о «-».
- Division лист. Как понятно из названия – это лист, обозначающий деление. Он отрисовывается в 4 этапа. Рисуется линия по центру, длиной как большее из значений длины числителя и знаменателя. Рисуется числитель так, чтобы он был прижат к линии нижним краем и был расположен по центру от всей длины линии (на случай, если знаменатель длиннее). Рисуется знаменатель так, чтобы он был прижат верхним краем к линии и был расположен по центру от всей длины линии (на случай, если числитель длиннее). И в конце передается отрисовка на те листы, что идут после деления.
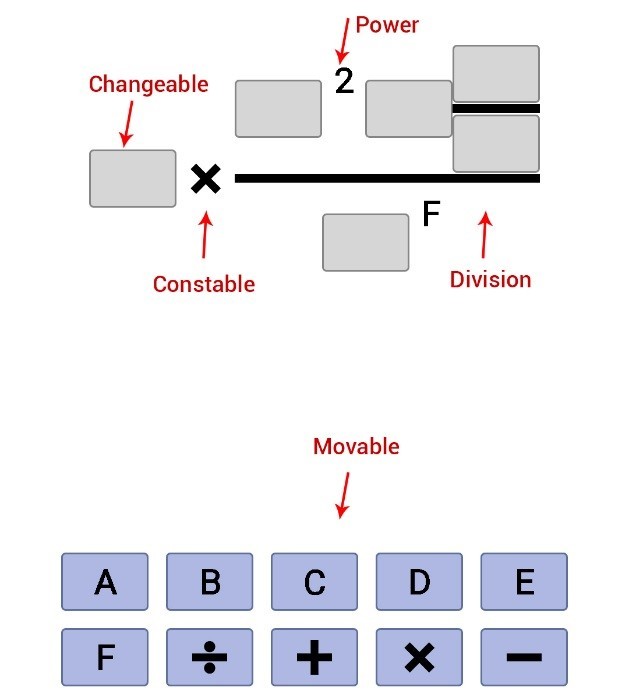
Чтобы логика работала, каждый лист должен уметь:
- Сказать свою длину и высоту
- Сказать длину и высоту себя и того, что находится за ним. Не просто следующего листа, а всей ветки листьев. То есть в формуле 2+3-4 знак «+» знает размеры части «+3-4». Это помогает определить размер всей формулы.
- Сказать, насколько ему надо сдвинуться от центра по оси Y (правило введено специально для Power листа)
- Уметь отрисовать себя и правильно передать координаты для отрисовки всем своим потомкам.
Этап второй — масштабирование блоков и текста
Чтобы максимально заполнить разрешенную область, перед отрисовкой идет этап масштабирования. Принцип прост. У меня есть единичный блок, на основе которого идут все расчеты и переменная, отвечающая за то, во сколько раз надо увеличить масштаб. Логика масштабирования такова: получаем размер формулы, сравниваем с размерами доступной области, изменяем коэффициент масштабирования.
И тут я столкнулся с небольшой проблемой. Ширина текста увеличивается не пропорционально атрибуту textSize. То есть, пусть у нас был блок текста шириной y и textSize x. Если мы увеличим textSize в 2 раза – ширина блока не будет равна 2*y. В связи с этим, значение масштабирования постоянно колебалось в близких значениях, из-за чего картинка при перерисовке «дрожала». Для решения этой проблемы я видел 2 способа:
- Можно было перед каждым шагом сбрасывать значение масштабирование в начальное значение. Но вариант меня не устроил, т к тогда погрешность размера по ширине была бы слишком большая.
- Ставить перед каждым шагом масштабирования формулу в одни и те же условия. Для этого я добавлял к коэффициенту 0.5 и округлял в большую сторону.
Пойдя по второму методу, я столкнулся с проблемой в самом первом расчете, когда коэффициент еще равен 1. Что бы решить это, поначалу, я делал расчет по второму методу 2 раза, но это сказалось на производительности. Чтобы избежать второго лишнего расчета, было решено сохранять предыдущее значение и сравнивать его с новым. Если они одинаковые, то второй раз считать смысла нет. Подумав еще, я вынес пересчет в метод onSizeChanged, а так же дополнительно вызывал при задании новой формулы/листов для движения.
Этап третий — движение
Здесь все очень просто. Была принята маленькая хитрость. Вместо движения листа, который мы выделили, мы скрываем его и заводим новый, координаты которого постоянно меняем при срабатывании onTouchEvent. Когда срабатывает MotionEvent.ACTION_DOWN, мы ищем, не попало ли наше касание на двигаемый лист, скрываем его и копируем значение в лист, который двигаем. Когда срабатывает MotionEvent.ACTION_UP, мы пробегаем по дереву и смотрим, не пересекаемся ли мы с каким-либо Changeable листом.
Этап четвертый — парсер
Тут в некой мере решение в лоб. Для начала было определено 2 спец. символа. Первый указывает на те блоки, которые станут Changeable. Второй символ — парный, указывает область, которую следует определить как Constable или Changeable без внутренних преобразований (например, символ деления). Получаем строку, удаляем все пробелы, что не входят в область выделенную вторым спец. символом, преобразуем знаки деления и начинаем посимвольно считывать. Чтобы можно было удобнее все преобразовывать, знаки деления из вида 2/3 преобразуются в /(2)(3).
Этап пятый – кастомизация
Для простоты кастомизации, почти все переменные, которые фигурируют в коде отрисовки или парсера, вынесены в отдельные поля классов. В связи с чем можно успешно поменять почти все, что видишь.
Заключение
Как оказалось, данная библиотека вполне подходит под «формулы» не только математические, но и, например, на проверку знаний словарных слов. Еще хотелось бы добавить на будущее, для тех кто тоже решит писать свои библиотеки – в android studio есть создание модуля-библиотеки, и удаляйте все из тега application в манифесте библиотеки. Если есть какие-либо вопросы – с радостью отвечу. Все замечания и пожелания учту.
Автор: KuSu






