«У современных мобильных телефонов такая же вычислительная мощь, что и у компьютеров NASA в 60-е годы. И в то время этого хватало, чтобы запустить человека в космос, а сегодня — только чтобы запускать птиц в свиней.»
Фольклор
«Вы назовете это извращением. Но кто сказал, что извращение — это плохо?»
Один доцент нашей кафедры
Идея описанного ниже эксперимента возникла после серии услышанных и подслушанных высказываний о том, что современные планшеты не могут выступать в роли инструментов серьезной научно-исследовательской деятельности. Действительно, для многих пользователей работа с планшетником сводится к веб-серфингу, переписке по электронной почте и разного протокола мессенджерах, чтению книг, просмотру видео и иным преимущественно развлекательным целям. Также, как следует ожидать и как показывает недавний пост, планшетник является прекрасным мобильным подспорьем при работе с «офисными» приложениями. Однако аппаратные характеристики существующей техники позволяют задуматься — а насколько же эффективным станет планшет на изначальном для компьютеров поприще.
Техника
Подопытным стал TeXeT TM-7025, с 1 ГГц процессором, 512 Мб оперативной памяти и Android 4.0 на борту. Мой первый компьютер, приобретенный в 2004 году, был чуточку мощнее (Athlon XP 1.66 ГГц, 256 Мб памяти до и 1 Гб — после апгрейда), однако заменен был только в марте 2012, намолотив Фортраном за свою жизнь расчётов на курсовую, а затем в паре с ноутбуком HP 550 — на два диплома, обеспечив успешное окончание школы, бакалавриата и магистратуры по направлению теоретической физики со специализацией на вычислительной гидродинамике.
Стоит сказать, что подопытный планшет имеет 7-дюймовый экран, что резко ограничивает удобство редактирования исходного кода, однако внешний компьютер для этих целей применялся по минимуму. Сторонними средствами написана уже данная статья, хотя, чего греха таить, введение и этот раздел набраны на смартфоне.
Софт
В силу рода занятий, возиться с портированием доступного софта не собирался даже в предельном случае разбора задачи. Потому, если бы такого не нашлось, то и эксперимента бы не было. Однако, обзор Google Play показал, что в нём наличествует порт Octave на Android. Помимо него, конечно же, имеется и весьма обширный спектр более простых программ, но с их вычислительными возможностями ясности нет, зато Octave — программа известная и небольшой опыт возни с ней уже имеется. Потому выбирать было не из чего, но возможность заодно разобраться и с этой системой более детально стала дополнительным стимулом в работе. Для рисования графиков имеющийся пакет требует установки графического пакета droidplot — портированной тем же автором версии gnuplot.
Естественно, код программы проще писать отдельным текстом и просто загружать его в консоли Octave. В качестве редактора был взял первый подвернувшийся под руку, то бишь бесплатная версия DroidEdit.
Задача
Пробные запуски были сделаны на системах дифференциальных уравнений. Просто загоняем систему и рисуем график на выходе, всё встроенными функциями Octave. Неинтересно, быстро. Но работает, что воодушевляет.
Тестовой стала небезызвестная система Лоренца, берущая своё начало, как известно, из уравнений конвекции в приближении Буссинеска.
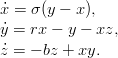
function xdot=f(x,t)
r=28.;
s=10.;
b=8./3.;
# система уравнений Лоренца
xdot(1)=s*(x(2)-x(1));
xdot(2)=r*x(1)-x(2)-x(1)*x(3);
xdot(3)=x(1)*x(2)-b*x(3);
endfunction
# временные границы, начальные условия
t=linspace(0.,10.,250);
x0=[7.;10.;5.];
lsode_options("integration method","non-stiff");
y=lsode("f",x0,t);
# график аттрактора в плоскости x-z
plot(y(:,1),y(:,3));
В зависимости от управляющего параметра (нормированного числа Рэлея), эта система проходит ряд устойчивых состояний от полного равновесия в нуле до хаотического режима. Сгенерированные на планшете картинки наглядно их демонстрируют. При r = 0.5:

r = 4:

r = 16:

r = 25:

r = 28:

Это всё замечательно, но какая вычислительная гидродинамика без конечно-разностных методов? Следующим этапом доказательства того, что планшет может не только потреблять контент, стало моделирование совершенно стандартной задачи конвекции жидкости в замкнутой полости. В рамках одного из курсов её обязан реализовать каждый студент наших кафедр. Формулировка следующая: рассчитать поле скорости и температуры несжимаемой вязкой жидкости в подогреваемой сбоку квадратной полости. По уму, конечно, разумно бы сперва посмотреть чего попроще, например, задачи теплопроводности, но решено было не мелочиться.
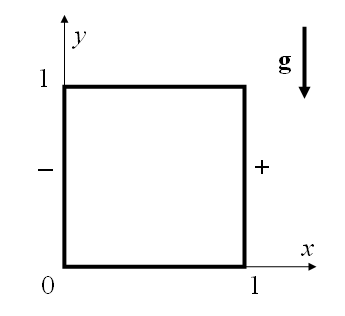
Уравнения сразу даны в безразмерном виде, сокращающем всё многообразие физических параметров задачи до двух — числа Грасгофа Gr и числа Прандтля Pr. На всех границах скорость, и значит — функция тока — равна нулю (условие прилипания для вязкой жидкости), температура слева — 0, справа — 1, на верхней и нижней границе линейно растёт.
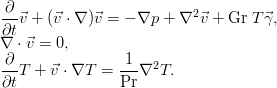
Для упрощения, задача рассматривается как двумерная — полость представляется бесконечно протяженным каналом квадратного сечения. Трёхмерные задачи — это гораздо более широкое богатство содержания, но в то же время уже совершенно иной уровень по требованиям к ресурсам, потому их численное моделирование широко развиваться стало только в последние пару-тройку десятилетий. Двумерный же подход позволяет выявить в первую очередь основные, всеобщие свойства гидродинамических систем, с гораздо меньшими усилиями. Прежде всего, связано это с особенностями двумерного течения жидкости — вместо векторных уравнений Навье-Стокса можно перейти к описанию скорости через две скалярные величины (т.н. двухполевой метод) — функцию тока (она же z-компонента векторного потенциала скорости) и завихренность (z-компонента ротора скорости). Примечательны они тем, что, во-первых, при переходе к функции тока автоматически и точно удовлетворяется условие несжимаемости (что и является основной проблемой моделирования в естественных переменных скорость-давление), а, во-вторых, с помощью функции тока крайне удобно изображать поле скорости — её изолинии соответствуют линиям тока, главное, разобраться с направлением течения.
Уравнения двухполевого метода:
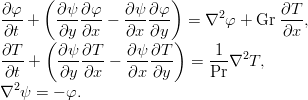
Программа
Программа незамысловата, и являет собой простейшую явную конечно-разностную схему. Потому останавливаться детально на ней незачем. Просто приведу исходник. Даже не особо оптимизированный, хотя с учётом производительности планшета вопросы оптимальности кода становятся крайне существенными.
a = 8.0;
ap = 8.0;
maxp = 100;
Nx = 10;
Ny = 10;
tmax = 10.;
Gr = 20000.;
Pr = 1.;
eps = 1.0e-2;
# выходные файлы
o1id = fopen("/sdcard/Octave/Convection/psi(t)_Gr=20000.txt","w");
o2id = fopen("/sdcard/Octave/Convection/field_Gr=20000.txt","w");
# массивы/матрицы
# завихренность
phi0 = zeros(Nx+1,Ny+1,"single");
phi1 = zeros(Nx+1,Ny+1,"single");
# функция тока
psi0 = zeros(Nx+1,Ny+1,"single");
psi1 = zeros(Nx+1,Ny+1,"single");
# температура
T0 = zeros(Nx+1,Ny+1,"single");
T1 = zeros(Nx+1,Ny+1,"single");
# вспомогательно-оптимизационные параметры
hx = 1.0 / Nx;
hy = 1.0 / Ny;
hxi = 1.0 / hx;
hyi = 1.0 / hy;
ht = hy**2/ a;
htp = hy**2 / ap;
htx2 = ht*hxi**2;
hty2 = ht*hyi**2;
htxy = 0.25*ht*hxi*hyi;
htpx2 = htp*hxi**2;
htpy2 = htp*hyi**2;
htpxy = 0.25*htp*hxi*hyi;
Pri = 1.0 / Pr;
# метки осей
x = linspace(0.,1.,Nx+1);
y = linspace(0.,1.,Ny+1);
axis("xy");
# начальное распределение
for i = 1:Nx+1
for j = 1:Ny+1
psi0(i,j) = 1.0e-1*(1.0d0 - (i-1)*hx)*(i-1)*hx*(1.0d0 - (j-1)*hy)*(j-1)*hy;
T0(i,j) = (i-1)*hx;
phi0(i,j) = 0.0;
endfor
endfor
ct = 0.;
q = 0;
# цикл по времени
while(ct <= tmax)
# уравнения для phi, T
for i = 2:Nx
for j = 2:Ny
dpsidx = psi0(i+1,j) - psi0(i-1,j);
dpsidy = psi0(i,j+1) - psi0(i,j-1);
phi1(i,j) = phi0(i,j) + ...
(phi0(i+1,j) - 2.*phi0(i,j) + phi0(i-1,j))*htx2 + ...
(phi0(i,j+1) - 2.*phi0(i,j) + phi0(i,j-1))*hty2 + ...
htxy*( dpsidx*(phi0(i,j+1) - phi0(i,j-1)) - dpsidy*(phi0(i+1,j) - phi0(i-1,j)) ) + ...
0.5*ht*hxi*Gr*(T0(i+1,j) - T0(i-1,j));
T1(i,j) = T0(i,j) + Pri*( (T0(i+1,j) - 2.*T0(i,j) + T0(i-1,j))*htx2 + ...
(T0(i,j+1) - 2.*T0(i,j) + T0(i,j-1))*hty2 ) + ...
htxy*( dpsidx*(T0(i,j+1) - T0(i,j-1)) - dpsidy*(T0(i+1,j) - T0(i-1,j)) );
endfor
endfor
# граничные условия
for i = 1:Nx+1
T1(i,1) = (i-1)*hx;
T1(i,Ny+1) = (i-1)*hx;
phi1(i,1) = -2.*Nx*Nx*psi1(i,2);
phi1(i,Ny+1) = -2.*Nx*Nx*psi1(i,Ny);
endfor
for j = 1:Ny+1
T1(1,j) = 0.;
T1(Nx+1,j) = 1.;
phi1(1,j) = -2.*Ny*Ny*psi1(2,j);
phi1(Nx+1,j) = -2.*Ny*Ny*psi1(Nx,j);
endfor
# уравнение Пуассона для функции тока
p = 0;
ppp0 = 0;
ppp1 = 0;
do
for i = 1:Nx+1
for j = 1:Ny+1
psi1(i,j) = 0.;
endfor
endfor
for i = 2:Nx
for j = 2:Ny
psi1(i,j) = psi0(i,j) + htp*phi1(i,j) + ...
(psi0(i+1,j) - 2.*psi0(i,j) + psi0(i-1,j))*htpx2 + ...
(psi0(i,j+1) - 2.*psi0(i,j) + psi0(i,j-1))*htpy2;
ppp0=ppp0 + abs(psi0(i,j));
ppp1=ppp1 + abs(psi1(i,j));
endfor
endfor
for i = 1:Nx+1
psi1(i,1) = 0.;
psi1(i,Ny+1) = 0.;
endfor
for j = 1:Ny+1
psi1(1,j) = 0.;
psi1(Ny+1,j) = 0.;
endfor
for i = 1:Nx+1
for j = 1:Ny+1
psi0(i,j) = psi1(i,j);
endfor
endfor
p = p++;
until(p > maxp || abs(ppp1 - ppp0)/(ppp0+ppp1) < eps)
for i = 1:Nx+1
for j = 1:Ny+1
phi0(i,j) = phi1(i,j);
psi0(i,j) = psi1(i,j);
T0(i,j) = T1(i,j);
endfor
endfor
# максимальное значение функции тока
if(q == 1000)
fprintf(o1id,"%f %fn",ct,max(max(psi0)));
q = 0;
endif
ct = ct + ht
q++;
endwhile
# поля переменных
for i = 1:Nx+1
for j = 1:Ny+1
fprintf(o2id,"%f %f %f %f %fn",(i-1)*hx,(j-1)*hy,psi0(i,j),T0(i,j),phi0(i,j));
endfor
endfor
fclose(o1id);
fclose(o2id);
# рисование и сохранение графиков
# в силу невыясненных причин потребовалось транспонировать выводимые матрицы
# как видно, генерируются картинки в eps-формате
# похоже, порт Octave пока попросту других делать не умеет
# можно строить в gnuplot / droidplot
figure(1);
contourf(x,y,T0');
title("T, Gr = 2000");
xlabel("x");
ylabel("y");
saveas(1,"/sdcard/Octave/Convection/T_20000.eps");
figure(1);
contourf(x,y,psi0');
title("Psi, Gr = 2000");
xlabel("x");
ylabel("y");
saveas(1,"/sdcard/Octave/Convection/psi_20000.eps");
Результаты
Ну, и самое интересное. Скорость и температура жидкости при различной интенсивности подогрева, то бишь — разных Gr. Решения получены на сетке размером 10х10 узлов. Конечно, это тоже немного, однако, когда компьютеры были большими, нормой бывали расчёты и на сетках 4х4, 5х5.
Со значениями основных параметров Gr ~ 10 000, Pr = 1, eps = 0.01 и кодом, приведённым выше, планшет обрабатывает одну единицу безразмерного времени в течение примерно трёх-пяти минут, что вовсе не так уж и медленно, с учётом недостатка памяти, необходимости Android'у выполнять иные системные функции и отвоёвывать на то ресурсы системы, а также и на потенциальную медлительность самой системы Octave как интерпретатора.
При больших Gr расчёт двухвихревого режима течения занимает гораздо больше времени из-за существенного ухудшения сходимости итерационного процесса. Вызвано это ухудшение тем, что двухвихревое течение является не стационарным, а установившимся колебательным процессом — вихри то усиливаются, то ослабевают, попутно изменяя свои размеры в довольно широком диапазоне. Например, Gr = 120 000 на планшете считается примерно часа полтора-два, но и на обычной машине процесс идёт не очень радостно по сравнению со слабым подогревом. Да и улететь в NaN на таком режиме уже легче лёгкого, требуется значительно уменьшать шаг времени. Ускорение алгоритма в данной ситуации — вопрос особый, и требует пересмотра метода решения разностных уравнений.
Итак, полученные картинки. Просто и наглядно — видно, что в полости существует устойчивое вихревое течение и выраженный перенос тепла в первую очередь за счёт движения жидкости — всплывания у нагретой границы и погружения у холодной. При повышении интенсивности подогрева течение сосредотачивается в пограничном слое и переходит в двухвихревой режим. Цветовая шкала не рисовалась, но она стандартная — рост от фиолетового к коричневому через зелёный (как на географических картах).
Функция тока и температура при Gr = 2000:
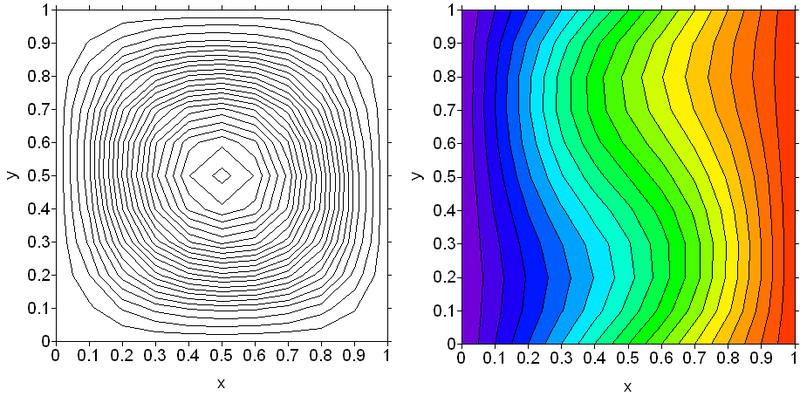
при Gr = 20000:
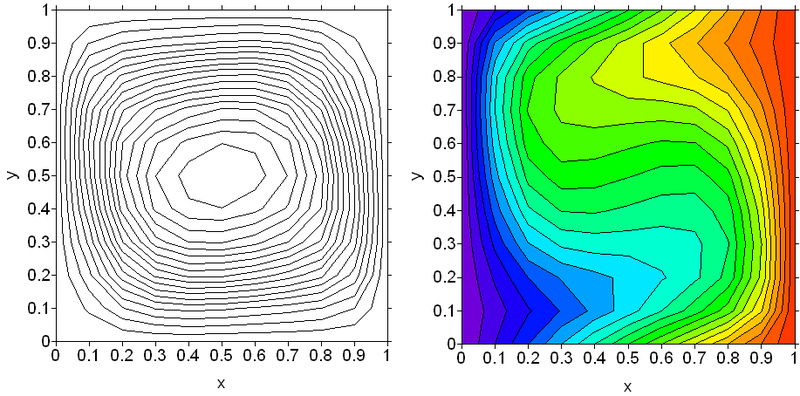
и при Gr = 120000:

Заключение
Планшет — действительно полноценная вычислительная машина. Слабенькая, но упорная. И производить на нём несложные вычисления, скажем, чтобы проверить свежую идею или прикинуть основные направления дальнейшего поиска, абсолютно реалистично.
Не стоит забывать, что любой компьютер всегда остаётся компьютером в изначальном смысле этого слова.
Автор: kbtsiberkin