Если вы когда-нибудь читали раздел помощь на Хабре, то наверняка видели там прелюбопытнейшую строчку:
Допустим, вы написали публикацию с рейтингом +100 — это добавило к вашему персональному рейтингу величину Х. Через несколько десятков дней этот самый Х вычтется, тем самым вернув вас на прежнее место.
то наверняка задавались вопросом, что это за Х и с какого он района чему он равен?
Сегодня мы ответим на этот вопрос.

(измеряем Хабра-рейтинг в попугаях)
Структура статьи:
- Аналитический вывод
- Регрессия
- Исключения
- Устойчивая регрессия
- Скрипт и данные
- Почему скрывать функцию бесполезно
- Что с этим можно сделать?
- Интерпретация формулы
Аналитический вывод
В данной части, мы рассмотрим основные свойства, которым должна удовлетворять любая функция рейтинга, и, используя наши знания о предметной области, попробуем догадаться до конкретного вида функции.
Основные предположения
От чего в принципе зависит рейтинг? Рейтинг любого пользователя формируется при помощи действий других пользователей, а точнее их голосования за карму, топики и комментарии. Других способов воздействовать на показатели пользователей у Хабра-жителей нет. Значит, что наша функция принимает на вход значение кармы (рациональное), голосов по топикам (целое) и комментариям (целое) и возвращает рациональное число.
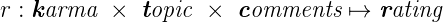
Более того, нам известно, что карма и голоса за комментарии и топики независимо друг от друга влияют на рейтинг, а значит, что наша тернарная функция распадается на некоторую композицию трех унарных. Предположим, что это некоторая сумма трех функций.
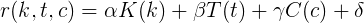
Каким граничным условиям должна удовлетворять любая функция рейтинга? Граничные условия — любой новый пользователь имеет рейтинг равный нулю; если пользователь не написал ни одного поста, значит, что вклад постов в рейтинг тоже равен нулю, etc.
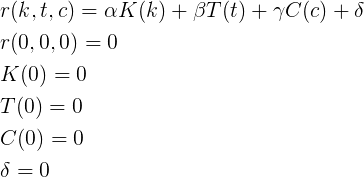
Что ещё мы знаем об этих функциях? Они должны быть монотонно возрастающими и простыми для вычисления (то есть как-то просто выражаться через элементарные функции). Рассмотрим самый простой вариант — линейная зависимость по каждому из параметров.
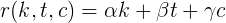
Вывод коэффициентов
Используя граничные условия, мы можем легко вывести эти коэффициенты. Рассмотрим случай, когда только карма имеет вклад в рейтинг (т.е., нет постов и комментариев за последние 30 дней).

Подставим альфу равной одной десятой в формулу:
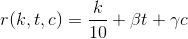
Получив первый коэффициент, мы можем взять другого пользователя, для которого один из неопределенных коэффициентов равен нулю и рассчитать второй коэффициент:

Подставим 4/5 за место беты в формулу:
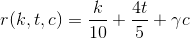
И последний штрих.
Финальная формула
Взяв любого другого пользователя, и подставив все параметры, получим, что гамма равна 1/100.
Тогда, функция рейтинга от кармы k, голосов за топики t и за комментарии c равна
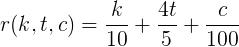
Регрессия
Понятно, что формула, выведенная по трем точкам, может быть неверна — есть бесконечное множество функций, проходящих через три точки. Поэтому эту гипотезу стоит проверить. Как? Давайте попробуем получить эти коэффициенты прямо из данных с помощью классической регрессии и сравнить с полученными.
Если наша гипотеза верна, то мы получим модель с коэффициентами сходными с аналитическими (и высокими параметрами уверенности в корректности модели).
Данные по рейтингу и соответствующим параметрам кармы, голосов за посты и комментарии (там много других интересных и вкусных данных по Хабру) доступны здесь:
github.com/SergeyParamonov/HabraData/blob/master/users_rating.csv
Приступим,
1478 users regular regression
Call:
lm(formula = rating ~ karma + topic_score + comment_score - 1, data = data)
Coefficients:
Estimate Std. Error t value Pr(>|t|)
karma 0.1017172 0.0006097 166.842 < 2e-16 ***
topic_score 0.7862749 0.0020999 374.428 < 2e-16 ***
comment_score 0.0153159 0.0031884 4.804 1.72e-06 ***
Как мы видим, значение коэффициентов по карме и постам фактически совпадает, причем, судя по параметрам, модель довольно уверена в оценке этих двух параметров. Но что же с третьим параметром (вклад комментариев в рейтинг)? И откуда вообще взялась разница в коэффициентах, если известно, что функция должна быть детерминированной?
Исключения
Казалось бы, классическая регрессия серьезно противоречит полученной нами формуле — расходится в оценке третьего параметра на 50% и не совпадает идеально по двум другим. Однако известно, что классическая регрессия невероятно неустойчива к статистическим выбросам. Давайте взглянем на них, то есть на набор точек, чьё значение рейтинга существенно отличается от полученной нами аналитической формулы.
>data$dif <- abs(rating - karma/10 - topic_score*0.8 - comment_score/100)
>print(data[data$dif > 2, ])
user rating karma topic_score comment_score dif
akrot 80.21 25.00 91 13 4.780
anegrey 60.30 31.50 114 15 34.200
Guderian 56.02 119.00 32 6 18.460
ilusha_sergeevich 154.27 157.75 177 11 3.215
ParyshevD 69.27 42.00 130 7 39.000
PatapSmile 48.75 246.00 0 0 24.150
rw6hrm 38.81 33.00 71 1 21.300
varagian 81.34 170.00 50 34 24.000
Тут можно заметить, что автор данной статьи находится в списке. Почему? Потому что имеется статья написанная 30 дней назад, а значит она не попала в выборку данных, но при этом голоса пропадают в течение трех дней. Отсюда возникает разница в рейтинге и показаниях полученной формулы.
Но это верно не для всех точек, например возьмём запись Guderian. У него не имеется граничных статей в последние 30 дней. Откуда же разница? Всё очень просто. TM неправильно посчитали ему рейтинг на Хабре, так как его статья переехала на megamozg, и как раз по ней у него есть недостающие голоса по статьям.
Бинго! Мы объяснили откуда берутся неподходящие точки:
- граничные статьи, написанные от 30 до 33 дней назад, с исчезающими голосами;
- переезды и деление Хабра;
- статьи, убранные в черновики или оффтопики (НЛО или автором).
Но всё это звучит, как подгонка под ответ, а не красивая верификация гипотезы, не правда ли? И тут на помощь нам приходит…
Устойчивая регрессия
Пусть у нас есть набор точек-выбросов в выборке и он небольшой, ну например до 5%, и достаточная выборка по пользователям (экспериментально хватает 1500 с верхом), то используем методы регрессии, устойчивой к выбросам (robust regression, а вот тут интересный KDD tutorial по теме).
Попробуем использовать метод прямо из коробки:
library("MASS")
...
Call: rlm(formula = rating ~ karma + topic_score + comment_score - 1, data = data)
Coefficients:
Value Std. Error t value
karma 0.10 0.00 23463021.30
topic_score 0.80 0.00 54494665.88
comment_score 0.01 0.00 448681.05
Вуаля, коэффициенты найдены и они в точности совпадают с полученными аналитически.
Скрипт и данные
Скачать можно здесь и применить на этих данных.
Для тех кому не хочется далеко ходить за скриптом:
library("MASS")
data <- read.csv("users.csv", header=T, stringsAsFactors=F)
names(data) <- c("user","rating","karma","topic_score","comment_score")
fit <- lm(data=data, rating ~ karma + topic_score + comment_score - 1)
print("regular regression")
print(summary(fit))
fit <- rlm(data=data, rating ~ karma + topic_score + comment_score - 1)
print("robust regression")
print(summary(fit))
attach(data)
data$dif <- abs(rating - karma/10 - topic_score*0.8 - comment_score/100)
print(data[data$dif > 2, ])
Почему скрывать функцию бесполезно
Тут конечно же внимательный читатель может сказать: «Ну вот, теперь TM придется придумывать новую тайную функцию подсчета рейтинга», и именно поэтому в этой части мы обсудим почему скрывать функцию рейтинга в принципе бесполезно.
Приведем основные свойства рейтинга:
- рейтинг зависит только от действий других пользователей и каналов для голосования, которых всего три: голоса за посты, комментарии и карму;
- голоса за посты, карму и комментарии независимы друг от друга т.е. функция всегда раскладывается в некоторую композицию трех независимых унарных функций от постов, комментариев и кармы;
- каждая из этих функций должна быть просто и быстро вычислима, так как показатели рейтинга нужно все время пересчитывать для большого числа пользователей;
- по этой же причине, она должна быть выразима в элементарных и монотонно возрастающих функциях;
- функция должна быть детерминированной и без шума, i.e., для двух пользователей с равными показателями кармы, голосов за посты и комментарии рейтинг должен быть одинаковый (за эффективный период = 30 дней).
Всё это позволяет по элементарно собранным данным восстановить эту функцию автоматически, используя методы устойчивой регрессии и подбора унарных функций отдельно друг от друга. Введение шума, недетерминированных элементов и вероятностей всего лишь немного усложнит задачу и возможно незначительно повлияет на точность параметров.
Security through obscurity и здесь не работает.
Что с этим можно сделать?
Когда я писал Хабра-монитор (это часть Хабра-аналитики, если вы пишите на Хабр, то возможно ресурс будет вам полезен), который отображает изменение параметров статьи во времени, первое, что хотелось прикрутить — это изменение голосов во времени. По ряду причин этот параметр недоступен для просмотра перед голосованием за пост. Имея аналитическую функцию для рейтинга пользователя, можно всегда вывести рейтинг его текущей статьи (при условии, что она одна и у него нет статей, по которым голоса «пропадают» в данный момент).
Фактически, имея данную функцию можно к монитору (картинка ниже) прикрутить параметр рейтинг статьи.
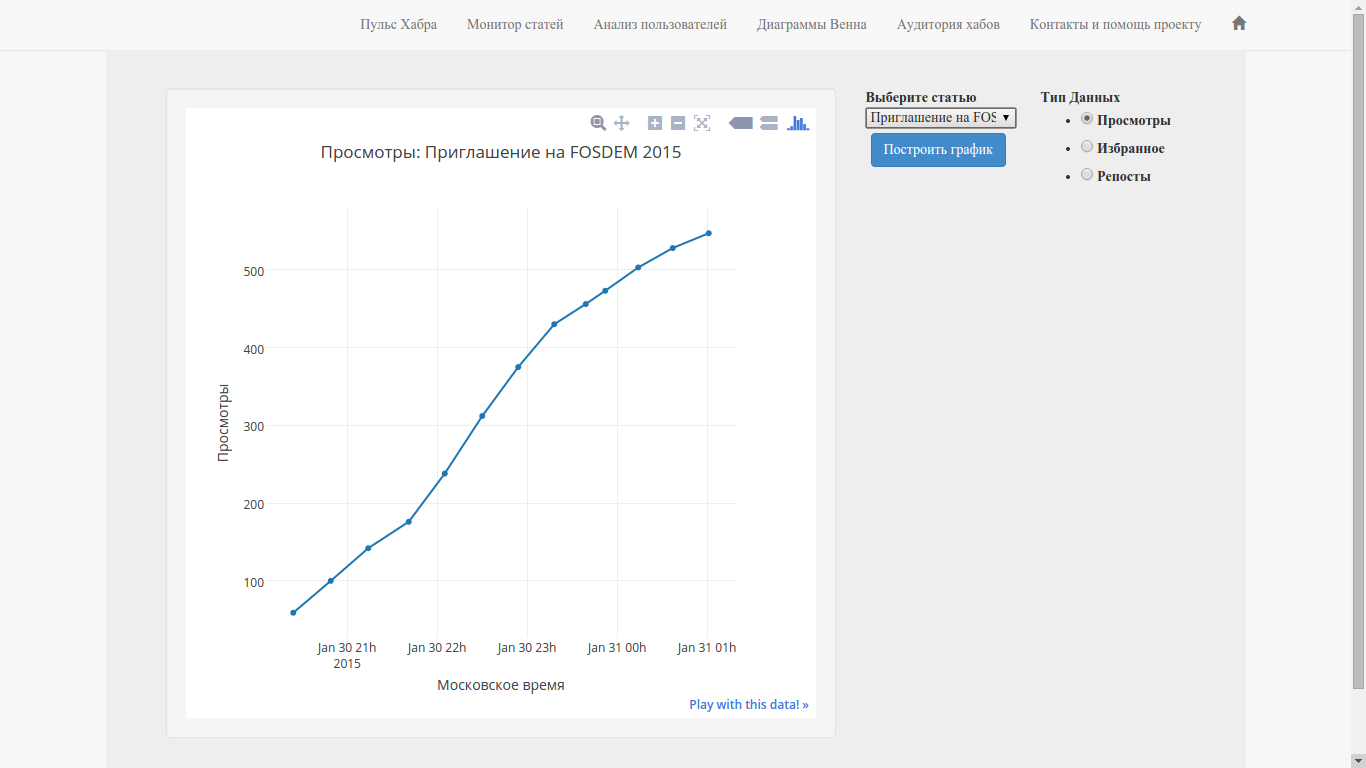
Еще это позволит СоХабру прикрутить рейтинг статей.
Интерпретация формулы
Голоса за комментарии практически не имеют вклада в рейтинг, даже самые рейтинговые комментарии за всю историю Хабра (~400+) прибавляют к рейтингу 4-5 очков, то есть столько же сколько статья набравшая 6-7 плюсов.
Карма потеряла свой вес по отношению к рейтингу, ранее у неё был коэффициент 0.5, а сейчас 0.1, что делает топ гораздо более динамичным (ранее войти в топ-10 было практически нереально).
Каждые 5 голосов за статью приносят 4 очка к рейтингу, то есть умножив на 0.8 голоса статьи, получим прибавку к рейтингу. На данный момент, это самый существенный и фактически единственный определяющий рейтинг пользователя фактор.
И ещё, Х = 80.
P.S. утверждение (отсюда)
[...] со временем рейтинг примет значение половины кармы.
уже неверно.
Автор: varagian