Нефтяные ряды в R

«Графики цен великолепны, чтобы предсказывать прошлое»
Питер Линч

С временными рядами мне как-то не доводилось иметь дело на практике. Я, конечно, читал о них и имел некоторое представление в рамках учебного курса о том, как в общих чертах проводится анализ, но хорошо известно, что то, о чем рассказывают в учебниках по статистике и машинному обучению, не всегда отражает реальное положение дел.

Вероятно, многие с интересом следят за теми пируэтами, которые выделывает кривая стоимости нефти. График выглядит то хаотично, то слишком уж регулярно, и делать какие-то предсказания по нему — весьма неблагодарное занятие. На временные ряды, безусловно, можно обрушить всю мощь статистических, экономико-математических и экспертных методов, но попробуем разобраться с техническим анализом — конечно, на базе R.
При работе с нормальными временными рядами можно использовать стандартный подход:

1. Визуальный анализ
2. Разложение ряда и изучение его компонент: сезонность, цикличность, тренд
3. Построение математической модели и прогнозирование

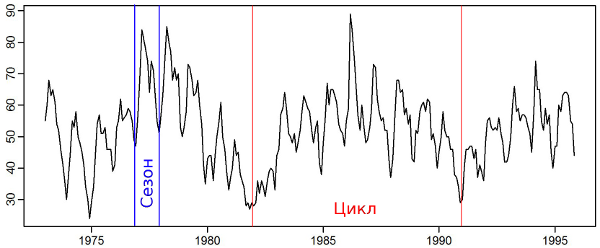
Есть весьма удобный источник данных — Quandl; он предоставляет интерфейс для Matlab, Python, R. Для R достаточно установить один пакет: install.packages("Quandl"). Меня интересует Europe Brent Crude Oil Spot Price — спотовая цена на нефть марки «Брент» (ниже используются три набора данных в разной детализации).

library(Quandl)
oil.ts <- Quandl("DOE/RBRTE", trim_start="1987-11-10", trim_end="2015-01-01", type="zoo")
oil.tsw <-Quandl("DOE/RBRTE", trim_start="1987-11-10", trim_end="2015-01-01", type="zoo", collapse="weekly")
oil.tsm <-Quandl("DOE/RBRTE", trim_start="1987-11-10", trim_end="2015-01-01", type="ts", collapse="monthly")
plot(oil.tsm, xlab="Year", ylab="Price, $", type="l")
lines(lowess(oil.tsm), col="red", lty="dashed")

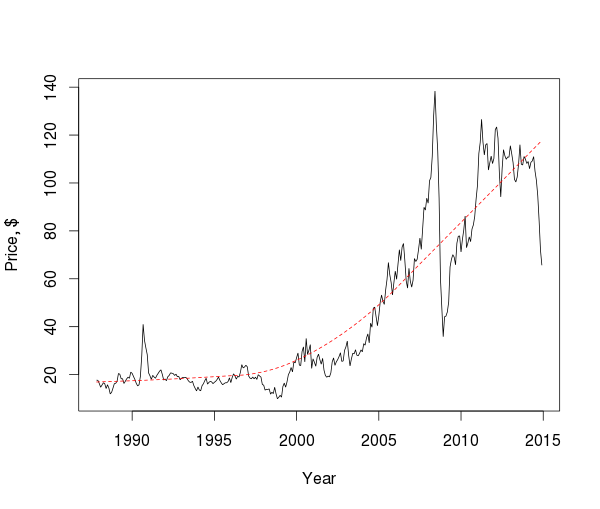
Если рассматривать цены в масштабе десятилетий, то можно заметить несколько пиков и падений и направление тренда, но в общем трудно сделать какие-то значимые выводы, поэтому исследуем компоненты ряда.

plot(decompose(oil.tsm, type="multiplicative"))

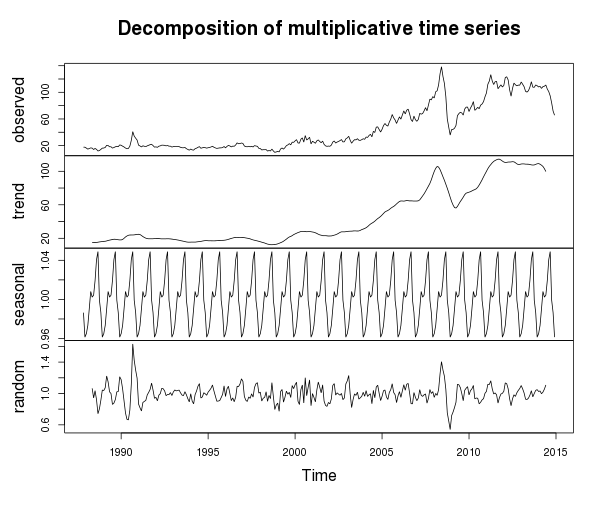
С трендом вроде бы все понятно — в 21 веке есть устойчивая до недавнего времени тенденция к росту (за исключением интересных годов), ряд нестационарный — это доказывает и расширенный тест Дикки-Фуллера:

>library(tseries)
>library(forecast)
>adf.test(oil.tsm, alternative=c('stationary'))

	Augmented Dickey-Fuller Test

data:  oil.tsm
Dickey-Fuller = -2.7568, Lag order = 6, p-value = 0.2574
alternative hypothesis: stationary

С другой стороны, с достаточно высокой степенью уверенности можно утверждать, что разности первого порядка ряда стационарны, т.е. это интегрированный временной ряд первого порядка (этот факт в дальнейшем позволит нам применить методологию Бокса — Дженкинса).

>adf.test(diff(oil.tsm), alternative=c('stationary'))

	Augmented Dickey-Fuller Test

data:  diff(oil.tsm)
Dickey-Fuller = -8.0377, Lag order = 6, p-value = 0.01
alternative hypothesis: stationary

> ndiffs(oil.tsm)
[1] 1

Кроме того, оказывается, есть и сезонная компонента, что трудно увидеть на общем графике. Если присмотреться, то кроме довольно высокой волатильности, можно заметить два скачка цен в течение года (что может быть связано с повышенным расходом нефти в зимний период и в сезон отпусков). С другой стороны, присутствует случайная компонента, вес которой особенно возрастает в критические годы (например, финансовый кризис 2008 г).
Иногда предпочтительнее работать с данными после однопараметрического преобразования Бокса-Кокса, которое позволяет стабилизировать дисперсию и привести данные к более нормальному виду:

L <- BoxCox.lambda(ts(oil.ts, frequency=260), method="loglik")
Lw <- BoxCox.lambda(ts(oil.tsw, frequency=52), method="loglik")
Lm <- BoxCox.lambda(oil.tsm, method="loglik")

Что же касается наиболее скользкой темы, а именно — экстраполяции, то в статье «Crude Oil Price Forecasting Techniques: a Comprehensive Review of Literature» авторы отмечают, что в зависимости от длины временного промежутка применимость моделей такова:

1. для среднесрочного и долгосрочного периода в большей степени походят нелинейные модели — те же нейронные сети, машины опорных векторов;
2. для краткосрочного периода ARIMA часто превосходит нейронные сети.

После всех формальностей воспользуемся как раз присутствующей в пакете forecast функцией nnetar(), с помощью которой без лишних сложностей можно построить нейросетевую модель ряда. При этом сделаем это для трех рядов — от более детализированного (по дням) до менее детализированного (по месяцам). Заодно посмотрим, что будет в среднесрочном периоде — например, за 2 года (на графиках это отображено синим цветом).

# Fit NN for long-run
fit.nn <- nnetar(ts(oil.ts, frequency=260), lambda=L, size=3)
fcast.nn <- forecast(fit.nn, h=520, lambda=L)

fit.nnw <- nnetar(ts(oil.tsw, frequency=52), lambda=Lw, size=3)
fcast.nnw <- forecast(fit.nnw, h=104, lambda=Lw)

fit.nnm <- nnetar(oil.tsm, lambda=Lm, size=3)
fcast.nnm <- forecast(fit.nnm, h=24, lambda=Lm)

par(mfrow=c(3, 1))
plot(fcast.nn, include=1040)
plot(fcast.nnw, include=208)
plot(fcast.nnm, include=48)

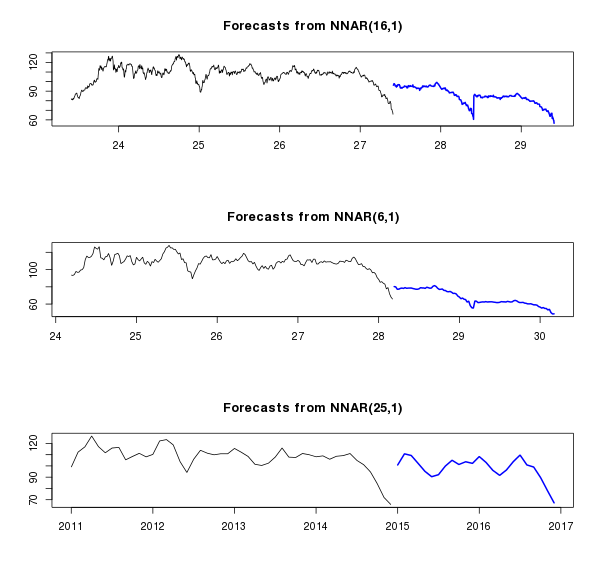
Что хорошо получилось на верхнем графике, так это переобучение: нейронная сеть отловила последний паттерн в ряду и принялась его копировать. На среднем графике сеть не только копирует последний паттерн, но еще и хорошо совмещает его с трендом, что придает некоторую реалистичность прогнозу. На нижнем графике получилась… какая-то невразумительная кривая. Графики хорошо иллюстрируют, как изменяются предсказания в зависимости от сглаживания данных. В любом случае для товаров с высокой (по разным причинам) волатильностью предсказаниям на такой временной промежуток верить нельзя, поэтому сразу перейдем к краткосрочному периоду, а заодно и сравним несколько разных моделей — ARIMA, tbats и нейронную сеть. Будем использовать данные за последнее полугодие и особенно выделим декабрь месяц в серию short.test — для целей тестирования.

# Fit ARIMA, NN and ETS for short-run
short <- ts(oil.ts[index(oil.ts) > "2014-06-30" & index(oil.ts) < "2014-12-01"], frequency=20)
short.test <- as.numeric(oil.ts[index(oil.ts) >= "2014-12-01",])
h <- length(short.test)

fit.arima <- auto.arima(short, lambda=L)
fcast.arima <- forecast(fit.arima, h, lambda=L)

fit.nn <- nnetar(short, size=7, lambda=L)
fcast.nn <- forecast(fit.nn, h, lambda=L)

fit.tbats <-tbats(short, lambda=L)
fcast.tbats <- forecast(fit.tbats, h, lambda=L)

par(mfrow=c(3, 1))
plot(fcast.arima, include=3*h)
plot(fcast.nn, include=3*h)
plot(fcast.tbats, include=3*h)

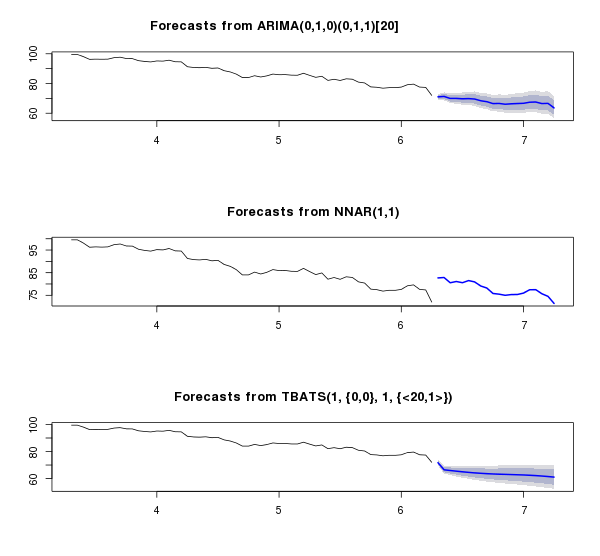
Нейронная сеть, переобучившись, несколько ушла в астрал, а ARIMA показала весьма интересную зависимость — интересную в плане близости к реальной картине. Ниже — сравнение предсказания каждой модели с реальными данными в декабре и mean absolute percentage error:

par(mfrow=c(1, 1))
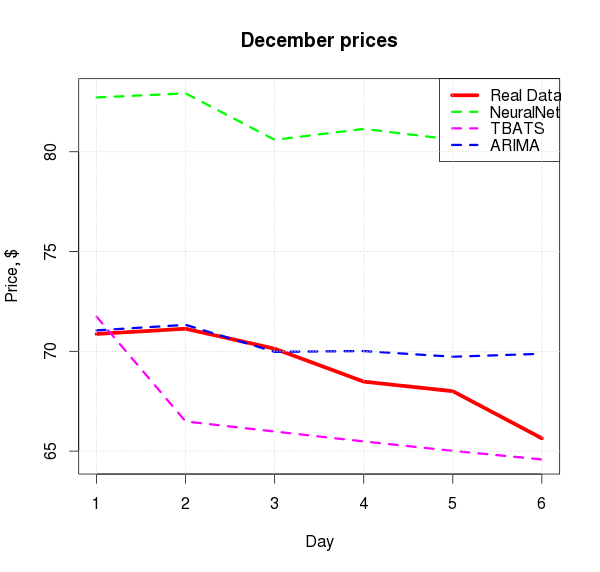
plot(short.test, type="l", col="red", lwd=5, xlab="Day", ylab="Price, $", main="December prices",
     ylim=c(min(short.test, fcast.arima$mean, fcast.tbats$mean, fcast.nn$mean),
            max(short.test, fcast.arima$mean, fcast.tbats$mean, fcast.nn$mean)))
lines(as.numeric(fcast.nn$mean), col="green", lwd=3,lty=2)
lines(as.numeric(fcast.tbats$mean), col="magenta", lwd=3,lty=2)
lines(as.numeric(fcast.arima$mean), col="blue", lwd=3, lty=2)
legend("topright", legend=c("Real Data","NeuralNet","TBATS", "ARIMA"), 
       col=c("red","green", "magenta","blue"), lty=c(1,2,2,2), lwd=c(5,3,3,3))
grid()

mape <- function(r, f){
  len <- length(r)
  return(sum( abs(r - f$mean[1:len]) / r) / len * 100)
}
mape(short.test, fcast.arima)
mape(short.test, fcast.nn)
mape(short.test, fcast.tbats)

Вместо заключения

Я не буду комментировать долгосрочные прогнозы: очевидно, что они уже неправильные и некорректные в данной ситуации. А вот ARIMA показала весьма неплохие результаты для краткосрочного периода. Также стоит обратить внимание на следующие факты. Нефть подешевела:

1. за сентябрь на 5%;
2. за октябрь — на 10%;
3. за ноябрь — на 15%;
4. за декабрь ...?

Это как бы намекает нам, что процесс изменения цены на нефть далек от процесса, который регулируется случайными параметрами.

Автор: kxx

Источник