Это третья статья в серии о применении R для статистического анализа данных, в которой будут разбираться представление и тестирование количественных данных. Вы узнаете как быстро и наглядно представить данные, а также как использовать t-тест в R.
Часть 1: Бинарная классифиация
Часть 2: Анализ качественных данных
Поехали!
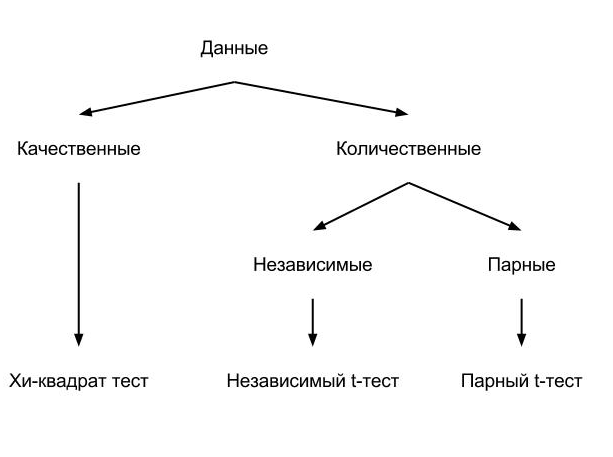
Для начала, я хочу еще раз привести схему из прошлой статьи:
 "
"
Парные данные отличаются тем, что данные для тестируемых групп были получены с одних и тех же объектов. Применения для t-теста: влияние какого-либо фактора на изменение продаж/скорости работы приложения/срок службы прибора, сравнение двух групп людей на продуктивность. Если групп несколько, то для анализа используют ANOVA-модели (ANOVA — analysis of variance), о который будет рассказано в следующих статьях.
Представление данных перед анализом
Начнем с того, как представить данные. Я использую имеющийся у меня файл одного медицинского теста, который я использовал по учебе. Кратко его опишу. Люди из двух групп, исследуемой и контрольной, делали некоторые упражнения. До и после упражнений измерялись их физиологические параметры. Мы попробуем проанализировать пульс и объем форсированного выдоха. Помимо t-тестов, я дополню предыдущую статью и покажу, как получить из чисел качественные данные. Итак:
tab <- read.csv(file="data1.csv", header=TRUE, sep=",", dec=".")
attach(tab)
tab
tab <- cbind(tab, pulsediff=pulse2-pulse1,
FEVcut2.5=cut(FEV1_1, c(0,2.5,max(FEV1_1)+0.1)))
str(tab)
detach(tab)
attach(tab)
Мы формируем дополнительный столбец с разностью пульса до и после, а также дополнительный столбец качественных данных для объема форсированного выдоха, который можно тестировать хи-квадрат тестом. Делается последнее функцией cut. В нее мы задаем данные и точки среза. На выходе:
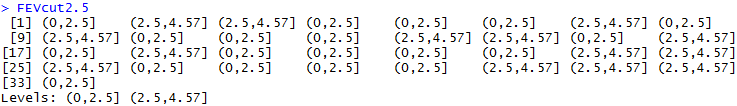 "
"
Идем далее. Посчитаем средние значения и стандартные отклонения, построим наглядные графики.
mean(pulsediff[group==0], na.rm=T)
mean(pulsediff[group==1], na.rm=T)
sd(pulsediff[group==0], na.rm=T)
sd(pulsediff[group==1], na.rm=T)
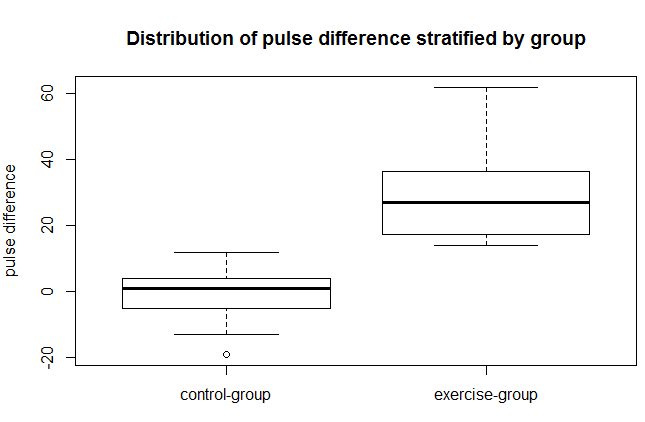
boxplot(pulsediff~group,
main="Distribution of pulse difference stratified by group",
names=c("control-group", "exercise-group"),
ylab="pulse difference")
Из важного хочу отметить, na.rm=T. Если в ваших данных присутствуют пустые ячейки, R самостоятельно их уберет. Иначе, вы получите ошибку. Boxplot — очень хороший метод для визуализации выборки. Он показывает максимум и минимум, среднее значение, а также квантили вероятности 25 и 75 процентов.
Теперь поговорим о разнице для парных и независимых данных с точки зрения статистики. В случае независимых данных, для анализа используется следующий доверительный интервал:
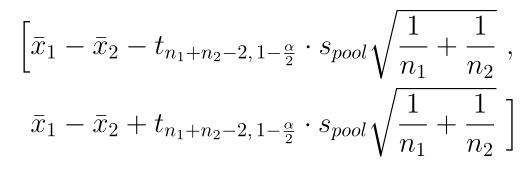
Среднее значение тут разность средних каждой выборки, а стандартное отклонение вычисляется по специальной формуле для разности.
В случае парных данных, мы вычитаем значения попарно и получаем новую выборку, у которой находим свое среднее значение и стандартное отклонение. Доверительный интервал:
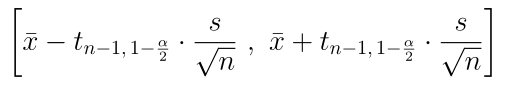
Применение тестов в R
#Paired data
#approach 1:
t.test(pulsediff[group==1])
t.test(pulsediff[group==0])
#approach 2:
t.test(pulse1[group==1], pulse2[group==1], paired=T)
t.test(pulse1[group==0], pulse2[group==0], paired=T)
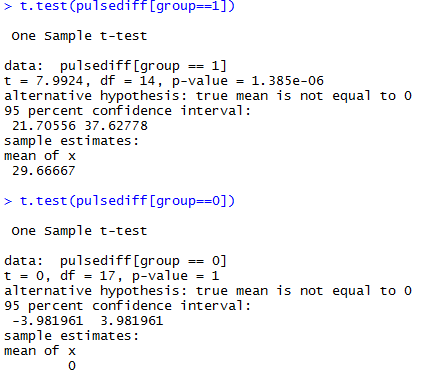
Тут мы смотрим на различия между пульсом до и после в одной группе. Можно использовать t.test двумя способами, либо посылая туда разность, либо два массива данных.
 "
"
Выводы: в группе 0 нет разницы до и после, в группе 1 разница есть, т.к. p-значение много меньше 5%.
#Unpaired data
t.test(pulsediff~group)
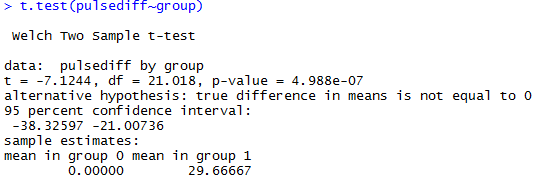
Тут мы анализируем разницу между группами. Данные независимые. Строго говоря, R использует тест Уелча, что немного отличается от обычного t-теста. Тест Уелча является более точным, они сходятся при большом размере выборки.
 "
"
Выводы: разница между группам существенная, т.к. p-значение много меньше 5%.
#Descriptive analysis:
library(prettyR)
str(FEVcut2.5)
str(sex)
xtab(sex~FEVcut2.5, data=tab)
#Inferential analysis:
chisq.test(table(sex, FEVcut2.5), correct=F)
#ADD:
chisq.test(table(sex, FEVcut2.5))
fisher.test(table(sex, FEVcut2.5))
Тут мы сравниваем объем форсированного выдоха у мужчин и женщин.
Таблица (из R gui, в RStudio у меня лично таблицы немного некорректно отображаются):
 "
"
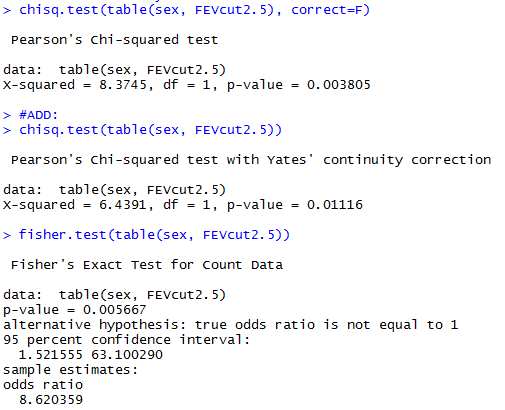
Результаты:
 "
"
Тут мы применили целых три теста, по возростанию сложности и точности. Я еще раз рекомендую пользоваться тестом Фишера, но имейте в виду и эти. Выводы: тесты дали разные результаты, однако p-значение все равно очень маленькое. Группы отличаются между собой.
Итоги
Итак, сегодня мы рассмотрели примеры использования тестов. Данной информации достаточно, чтобы проводить достаточно качественные статистические исследования. Эти методы можно применять в любых областях. Их использование убережет вас от ошибок, позволит объективно оценить свою работу и предоставлять другим людям объективно достоверную информацию. Есть еще несколько тем, которые я хочу осветить, касающиеся оценки необходимого размера выборки, доказательства равенства случайных величин и ANOVA-моделей.
Автор: aledovskiy