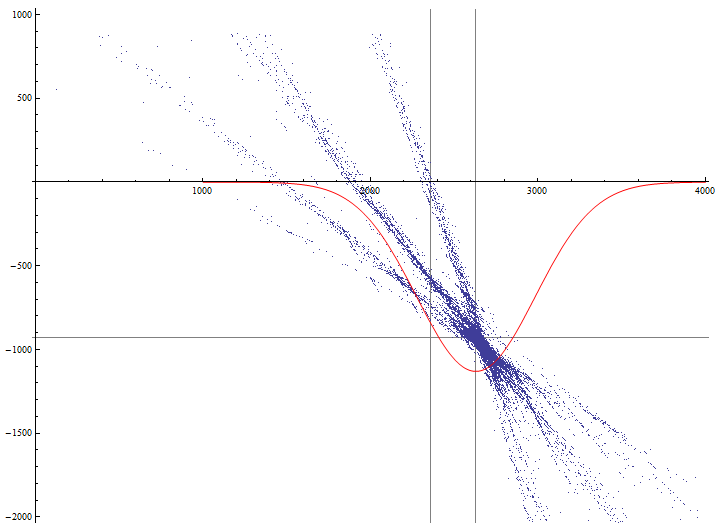
В прошлый раз мы загрузили данные из файла, разобрали их в структуру, получили уравнения треков движения ТС и графически отобразили эти данные: Часть 1
В данной статье одним из методов найдем статистически точку, в окрестностях которой пересекаются треки движения ТС.
Описание одного из способов нахождения интересующей нас точки
В данном методе найдем все точки пересечения графиков — треков движения ТС, найдем математическое ожидание этих данных и дисперсию.
Нахождение всех точек пересечения треков
Определим количество уравнений в списке с уравнениями:
length = Length[numeq];
Создадим пустой список, в который будем записывать координаты точек пересечения трэков:
rootlist = {};
Теперь необходимо написать цикл. который будет решать попарно имеющиеся у нас линейные уравнения и находить координаты их пересечения и записывать в подготовленный список::
Do[Do[rootlist = Append[rootlist, List[
x /. Solve[numeq[[j]] == numeq[[i]], x][[1]],
numeq[[j]] /. Solve[numeq[[j]] == numeq[[i]], x][[1]]
]
]
, {i, 1 + j, length}],
{j, 1, length}]
На каждом проходе цикла мы добавляем к rootlist список, состоящий из координаты x и y пересечения j и i уравнения, при этом координата x находится как:
x /. Solve[numeq[[j]] == numeq[[i]], x][[1]]
, при этом
Solve[numeq[[j]] == numeq[[i]], x]
возвращает список корней данного уравнения:
{{x -> 2586.14}}
, а наша запись выделяет первый корень, он тут единственный, и выполняет подстановку, т.е. вместо x перед оператором /. подставляется его значение x -> 2586.14.
expr /. x > value – в выражение expr вместо переменной x подставляется ее
значение value.
Таким образом находится координата X пересечения двух треков, аналогичное действие производится и для нахождения координаты Y, только значение корня теперь подставляется в одно из уравнений, в данном случае в индексом j, при этом это может быть и уравнение с индексом i:
numeq[[j]] /. Solve[numeq[[j]] == numeq[[i]], x][[1]]
Далее округлим значение наших точек до целого:
rootlist = Round[rootlist];
Теперь мы имеем список точек пересечений трэков и можемпристапать к статистической обработке.
Список выглядит таким образом:
{{2586, -910}, {2716, -1014}, {2718, -1015}, {3566, -1697}, {2697, -999}, {2957, -1207}, ... }
Статистическая обработка результатов
Определим мат ожидание координаты X списка пересечений:
Xmed = Mean[rootlist[[All, 1]]] // N
2532.7
Mean[data] – возвращает среднее значение данных data.
N[expr, n] — возвращает результат вычисления выражения expr с точностью до n знаков после десятичной точки
x // f — Постфиксная форма для f[x]
Определим дисперсию координаты X списка пересечений:
sX = StandardDeviation[rootlist[[All, 1]]] // N
81038.5
StandardDeviation[data] – возвращает стандартное отклонение данных, говоря русским языком — функция возвращает сигму, ну или среднеквадратичное отклонение.
Определим те же характеристики для Y координаты пересечения:
Ymed = Mean[rootlist[[All, 2]]] // N
sY = StandardDeviation[rootlist[[All, 2]]] // N
-699.907
106488
Из полученных данных математических ожиданий уже можно определить искомые величины — угол поворота видеокамеры относительно края обочины:
Xangle = Xang Xmed/Xlen - Xang/2 // N
8.02449
, и угол наклона видеокамеры относительно траекторий движения транспортных средств
Yangle = Abs[Yang Ymed/Ylen - Yang/2] // N
9.38796
Вообще, такое большое значение среднеквадратичного отклонения несколько смущает. построим гистограмму что-бы посмотреть распределение величин и выяснить, почему так происходит:
Histogram[
{rootlist[[Range[length], 1]],
rootlist[[Range[length], 2]]},
100, AspectRatio -> 1]
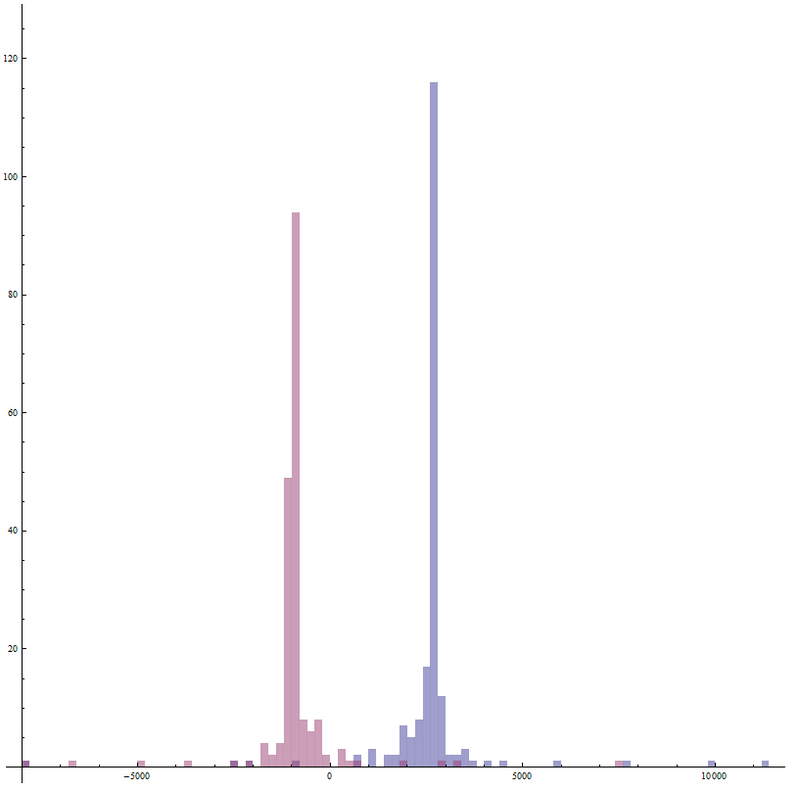
Histogram[list,bspec] — строит гистограмму списка list с количеством столбцов bspec
Из данной гистограммы видно, что есть точки пересечения, находящиеся далеко от математического ожидания величины.
Попробуем не принимать во внимание точки, не удовлетворяющие следующими условию:
X координата точки должна лежать в пределах [-разрешение камеры по горизонтали; 2 разрешения камеры по горизонтали]
Y координата точки должна лежать в пределах [- 2 разрешения камеры по вертикали; 0.5 разрешения камеры по вертикали]
Для этого напишем следующее:
length = Length[rootlist];
rlist = {};
Do[If[
-Xlen < rootlist[[i, 1]] < 2 Xlen && -2 Ylen < rootlist[[i, 2]] < 0.5 Ylen,
rlist = Append[rlist, rootlist[[i]]]]
, {i, length}]
If[condition, t, f] – возвращает t, если результатом вычисления condition будет True, и даст f, если результат False
And[p,q,...] или p && q && ... — логическое сложение – операция «И»;
Оценим мат ожидание и среднеквадратичное отклонение получившейся отфильтрованной выборки:
Xmed = Mean[rlist[[Range[length], 1]]] // N
Ymed = Mean[rlist[[Range[length], 2]]] // N
sX = StandardDeviation[rlist[[Range[length], 1]]] // N
sY = StandardDeviation[rlist[[Range[length], 2]]] // N
2628.84
-928.819
353.112
457.717
Получившийся разброс отфильтрованной выборки меньше, чем у полной выборки. Определить искомые углы можно так-же, как и в случае с полной выборкой.
Графическое представление результатов
Теперь отобразим на одном графике точки пересечения по отфильтрованной выборке и функцию распределения координаты X точек пересечения:
lp = ListPlot[rlist, PlotStyle -> PointSize[0.0005], GridLines -> {{Xlen, Xmed}, {Ylen, Ymed}}, AspectRatio -> Automatic];
dp = Plot[-1000000 PDF[NormalDistribution[Xmed, sX], x], {x,1000, 4000}, PlotStyle -> {Red}];
Show[lp, dp, PlotRange -> {{0, 4000}, {-2000, 1000}}, AxesOrigin -> {0, 0}]
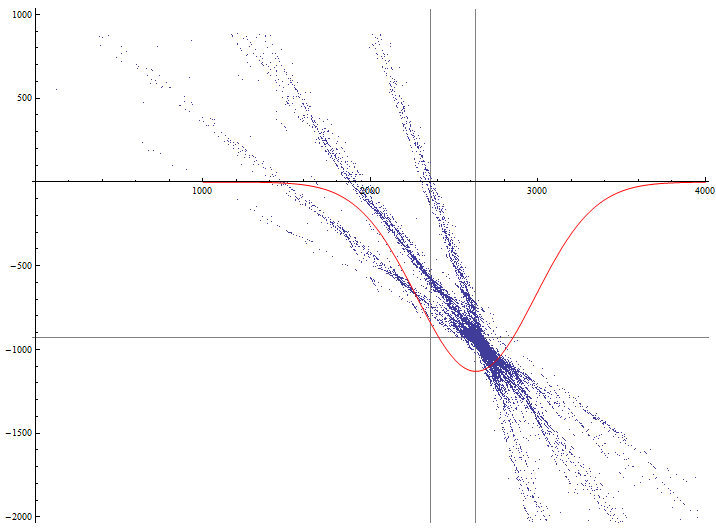
PDF[dist,x] – возвращает значение плотности вероятности распределения при аргументе x и заданном законе распределения dist
NormalDistribution[mu,sigma] – нормальное распределение
Я немного схитрил и поставил коэффициент -1000000 для наглядности графика.
Что дальше?
В следующей статье я покажу иной способ определения точки пересечения, основанный на фильтрации уравнений и нахождении подмножеств внутри множества.
Автор: ZarkSpb






