Постановка задачи
Имеется система, размещающаяся над дорожным полотном, включающая в себя видеокамеру. Известны разрешение видеокамеры и углы обзора. Относительно дорожного полотна видеокамера устанавливается следующим образом: сверху над любой из полос движения, сбоку от дорожного полотна не далее, чем 3 метра от края ближайшей контролируемой полосы движения. Количество одновременно контролируемых полос движения — не более 4. Видеокамера производит фотографирование зоны контроля с определенной частотой кадров. Все сделанные кадры поступают на вход системы распознавания номерных знаков. Результатом проезда транспортного средства (далее по тексту -ТС) является трек с координатами центра рамки номерного знака ТС в виде:
x11 y11 x12 y12 … x1i y1i … x1n y1n
Результатом проезда нескольких ТС является файл треков в виде:
x11 y11 x12 y12 … x1i y1i … x1n y1n
x21 y21 x22 y22 … x2i y2i … x2n y2n
...
xi1 yi1 xi2 yi2 … xii yii … xin yin
...
xn1 yn1 xn2 yn2 … xni yni … xnn ynn
Пример файла треков:
1420 23 1399 44 1377 62 1351 82
417 327 368 359 313 392 119 500 48 540
2300 62 2291 91 2275 125 2267 159 2254 197
2298 114 2263 223 2199 413 2180 470 2158 532
Необходимо, имея файл с выше описанной структурой, определить угол наклона видеокамеры относительно траекторий движения транспортных средств и поворота видеокамеры относительно края обочины.
Импорт данных
Импортируем данные, с которыми будем работать.
Наш файл лежит в директории, из которой запускается ноутбук (документ Mathematica), называется файл recdat.txt. Для импорта введем:
file = Import[NotebookDirectory[] <> "recdat.txt", "Table"];
file — переменная, в которую происходит импортирование файла
NotebookDirectory[] — возвращает директорию, в которой находится ноутбук в виде строки
<> — сокращенная запись функции, соединяющей строки
"recdat.txt" — строка, указывающая имя файла с треками
"Table" — опция функции Import[], указывающая на то, что данный файл необходимо импортировать в виде таблицы, соответственно переменная file будет иметь тип таблицы (списка)
Символ ; в конце строки говорит о том, что Mathematica не будет выводить результат выполнения описанной функции после ее выполнения.
Нажатие Shift+Enter приведет к импортированию нашего файла.
Что-бы посмотреть, как именно импортировались данные необходимо ввести file и нажать Shift+Enter, но для более наглядного отображения информации мы воспользуемся следующей функцией:
TableForm[file]
1420 23 1399 44 1377 62 1351 82
417 327 368 359 313 392 119 500 48 540
2300 62 2291 91 2275 125 2267 159 2254 197
2298 114 2263 223 2199 413 2180 470 2158 532
TableForm[list] — выполняет вывод с элементами списка list, расположенными в массиве прямоугольных элементов
Определяем константы, задающие разрешение видеокамеры и углы обзора:
Xlen = 2360; (*Горизонтальное разрешение камеры*)
Ylen = 1776; (* Вертикальное разрешение камеры*)
Xang = 14; (*Горизонтальный угол обзора камеры*)
Yang = Xang*3/4; (*Вертикальный угол обзора камеры*)
Определяем количество треков в файле:
length = Length[file];
Length[list] — возвращает число элементов одномерного списка list или число размерностей в случае многомерного списка
Раскладывание импортированных данных в структуру
Импортированные данные представляют из себя структуру, с которой неудобно работать в Mathematica. Гораздо удобнее с ними будет работать, если разложить их в структуру в виде трехмерного списка, где элемент с индексом i,j состоит из двух элементов — x- и y-координаты центра номерного знака, при этом i — порядковый номер номерного знака, а j — порядковый номер точки трека для i-го номерного знака.
Небольшое отступление от темы:
В Mathematica одно и тоже действие можно сделать разными способами, т.к. среда включает в себя огромный набор различных функций; одно и тоже действие можно сделать с помощью цикла, а можно и используя специальную функцию Mathematica. Как правило, время выполнения действия, нацеленного на один и тот-же функционал меньше при выполнении его с помощью стандартной функции Wolfram, нежели при выполнении его с помощью самописного цикла. Время выполнения функции или набора функций помогает определить функция
Timing[].
Для создания списка, в который мы будем раскладывать структуру сначала объявим переменную как список:
num = {};
Для раскладывания в структуру наших данных напишем цикл:
Do[num = Append[num,
Partition[file[[i]], 2]],
{i, length}]
Do[действие, {условие выполнения цикла}]
Append[list,element] – добавляет элемент в конец списка
Partition[list,n] – разбивает список list на не перекрывающиеся части с длиной n. Если количество элементов в списке не делится нацело на n, то последние k (k<n) элементов удаляются.
file[[i]] — возвращает i элемент списка
Теперь обратимся к уже знакомой нам функции, и посмотрим, как выглядит структура, удобная для дальнейшей обработки:
TableForm[num, TableSpacing -> {3, 4}]
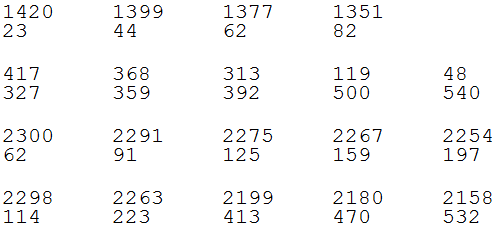
TableSpacing -> {3, 4} — задает отступы между элементами списка при отображении
Получение уравнений треков
В частном случае точки трека необходимо линеризовать. «В частном» — потому, что рассматриваемые выше данные были получены на прямой дороге, где ТС движутся с большими скоростями, и за время проезда зоны контроля просто физически на такой скорости не могут двигаться по траекториям, сильно отличающимся от прямолинейных.
Уравнения движения ТС мы будем записывать в список. Для этого сначала его объявим:
numeq = {};
И напишем функцию для определения уравнений движения ТС через зону контроля. Тут необходимо сказать, что начало координат в кадре — это левый верхний угол кадра, итак:
Do[numeq = Append[numeq,
Fit[num[[i]], {1, x}, x]],
{i, length}]
Fit[data, funs, vars] – для списка данных data ищет приближение методом наименьших квадратов в виде линейной комбинации функций funs переменных vars. Данные data могут иметь форму {{x1,y1,...,f1}, {x2,y2,...,f2}, ...}, где число коор динат x,y,… равно числу переменных в списке vars. Также данные data могут быть представлены в форме {f1, f2, ...} с одной координатой, принимающей значения 1,2,… Аргумент funs может быть любым списком функций, которые зависят толь ко от объектов vars.
В нашем случае мы для каждого i-го элемента многомерного списка num, содержащего двумерный массив точек — центров номерного знака ТС — определяем методом наименьших квадратов функцию вида kx+b наиболее близкую к имеющемуся набору точек.
Результатом выполнения данного цикла является список, примерно представляющий из себя следующее:
{1167.11 - 0.803101 x, 568.193 - 0.571513 x, 6110.1 - 2.62293 x, 6471.36 - 2.75496 x, 1199.09 - 0.812067 x, 2491.96 - 1.29425 x, 1121.33 - 0.787616 x, 2933.43 - 1.75218 x, 625.959 - 0.609492 x, 2512.3 - 1.30408 x, 7805.9 - 3.3897 x, 881.413 - 0.698268 x, 2651.99 - 1.3463 x, 6140.19 - 2.61239 x, 2594.17 - 1.27645 x, 557.83 - 0.587095 x, 1195.29 - 0.82697 x, 6346.13 - 2.73884 x, 6887.01 - 2.92561 x, 2377.62 - 1.26743 x, 3241.53 - 1.72441 x, 1424.49 - 0.846298 x, 1218.75 - 0.83174 x, 7203.35 - 3.089 x, 5420.94 - 2.28441 x, 2500.74 - 1.29295 x, 2402.61 - 1.25934 x, 6760. - 2.89566 x, 1175.7 - 0.794353 x, 1117.2 - 0.77705 x, 7066.9 - 3.00537 x, 2346.99 - 1.24765 x, 2698.98 - 1.39178 x, 1277.43 - 0.849703 x, 633.372 - 0.61772 x, 2578.56 - 1.3082 x, 2952.21 - 1.47007 x, 1107.8 - 0.7861 x, 2352.46 - 1.24075 x, 2326.56 - 1.23348 x...}
Графическое представление данных и прямых по списку уравнений
После получения уравнений мы можем отобразить на графике все имеющиеся у нас точки и соответствующие им уравнения.
Для отображения на графике списка точек в Mathematica есть функция ListPlot[], а для отображения функций есть функция Plot[]. Для того, что-бы на одном графике отобразить график с точками и графики функций, или для переопределения параметров графиков есть функция Show[]. Напишем эти функции для нашего случая:
eqlineplot = Plot[numeq[[Range[length]]], {x, 0, Xlen}];
numplot = ListPlot[num[[Range[length]]]];
Show[
eqlineplot,
numplot,
AspectRatio -> 3/4, Frame -> False,
PlotRange -> {{0, Xlen}, {0, Ylen}}]
И результат ее выполнения:
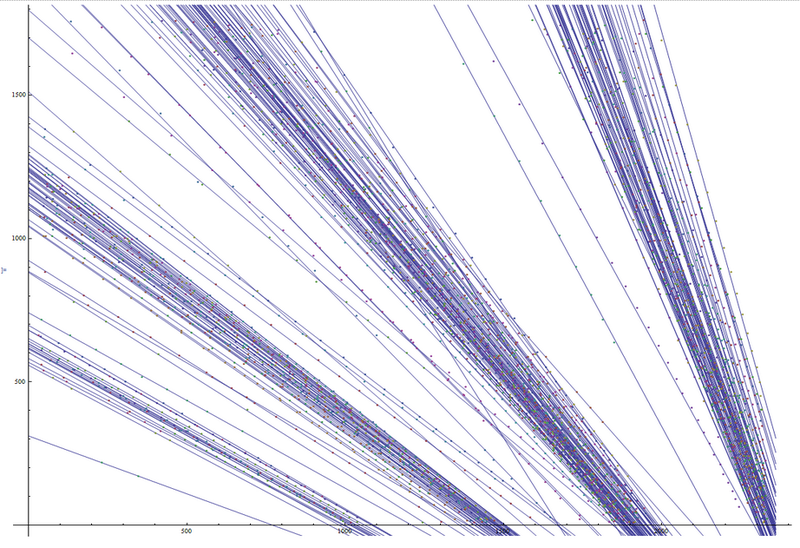
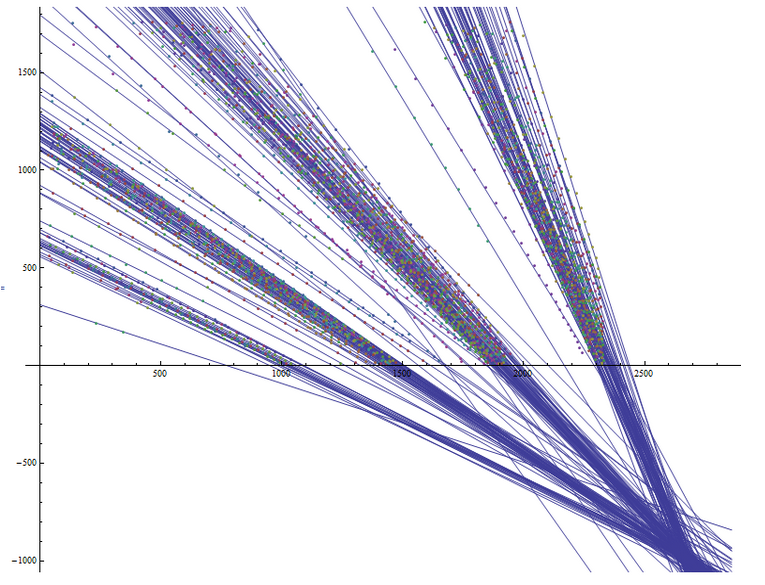
Этот график реверсивен относительно оси OX, т.к. у него точка начала координат находится в нижнем левом крае, а не как у камеры — в верхнем левом. Но это не мешает понять, что линии пересекаются где-то в окрестности одной точки — точки, от которой мы дальше будем отсчитывать углы. Ниже показан график с немного измененными областями прорисовки, на котором видно пересечение линий в окрестностях одной точки:
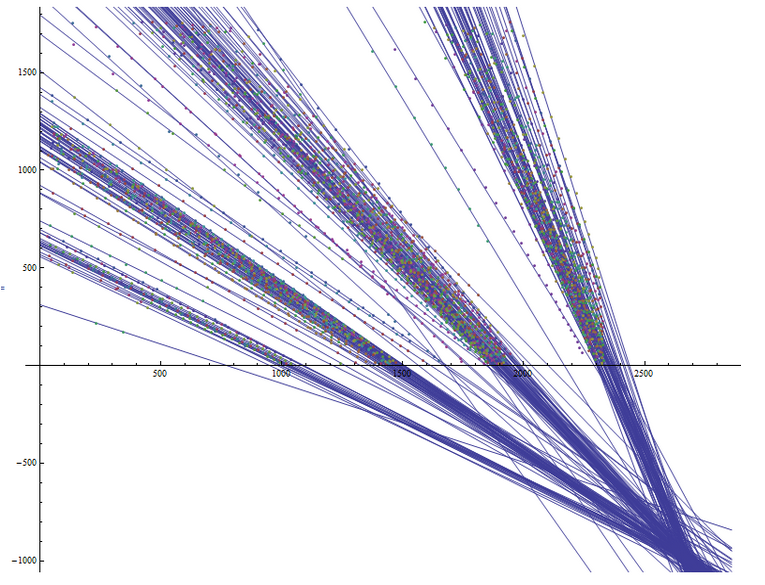
Немного подробнее рассмотрим записи функций:
eqlineplot = Plot[numeq[[Range[length]]], {x, 0, Xlen}];
Plot[список функций, которые отобразятся на графике,
{переменная, отностильно которой строятся функции,
ее минимальное значение,
ее максимальное значение}]
Range[imax] – генерирует список числовых элементов {1, 2, ..., imax}
Show[
eqlineplot,
numplot,
AspectRatio -> 3/4, Frame -> False,
PlotRange -> {{0, Xlen}, {0, Ylen}}]
AspectRatio -> 3/4 — устанавливаем воотношения сторон графика
PlotRange -> {{0, Xlen}, {0, Ylen}} устанавливаем диапазон прорисовки графиков по координатам X и Y
Frame -> False — сообщаем Mathematica, что вокруг графика не надо чертить рамку.
Что дальше?
В продолжении, если вам покажется интересным и необходимым, я расскажу о нескольких методиках нахождения точек пересечения графиков, познакомлю вас со статистической обработкой данных и анализом данных на примере рассматриваемой задачи.
Автор: ZarkSpb






