Привет, в одной из последних лекций по нейронным сетям на курсере речь шла о том, как можно улучшить сходимость алгоритма обратного распространения ошибки в общем, и в частности рассмотрели модель, когда каждый вес нейрона имеет свою собственную скорость обучения (neuron local gain). Я давно хотел реализовать какой нибудь алгоритм, который бы автоматически настраивал бы скорость обучения сети, но все лень руки не доходили, а тут вдруг такой простой и незамысловатый способ. В этой небольшой статье я расскажу про эту модель и приведу несколько примеров того, когда эта модель может быть полезна.
Теория
Начнем с теории, для начала вспомним чему равно изменение одного веса, в данном случае с регуляризацией, но сути это не меняет:
- эта (η) — скорость обучения
- m — размер обучающего множества
- n — номер слоя
- полная нотация тут
В базовом случае скорость обучения — это глобальный параметр для всех весов.
Введем для каждого веса каждого нейрона модификатор скорости обучения , а изменять веса нейронов будем по следующему правилу:
На первом батче обучения все модификаторы скорости обучения приравниваются к единице, далее динамическая настройка модификаторов в процессе обучения происходит следующим образом:
- — значение градиента в определенный момент времени
- тау τ — текущий момент времени или текущий батч обучения
- b — аддитивный бонус, который получает модификатор, если направление градиента по определенной размерности не меняется
- p — мультипликативный штраф, в случае смены направления вектора градиента
Имеет смысл бонус делать очень маленьким числом меньшим единицы, а пенальти , таким образом b + p = 1. Например a = 0.05, p = 0.95. Такая настройка гарантирует, что в случае осцилляции направления вектора градиента, значение модификатора будет стремиться обратно к начальной единице. Если не вдаваться в математику, то можно сказать так, что алгоритм поощряет те веса (рост в рамках какой то размерности пространства весов) которые сохраняют свое направление относительно предыдущего момента времени, и штрафует тех, кто начинает метаться.
Автор этого метода Geoffrey Hinton (он кстати один из первых предложил использовать градиентный спуск для обучения нейронной сети) так же советует учесть следующие вещи:
- во-первых стоит задать разумные пределы роста для модификаторов
- во-вторых не стоит использовать этот прием для онлайн обучения, или для маленьких батчей; нужно что бы в процессе батча аккумулировался достаточно общий градиент; а иначе увеличивается частота осцилляции направления, и тем самым теряется смысл в модификаторе
Эксперименты
Все эксперименты проводились на множестве картинок 29 на 29 пикселей, на которых нарисованы английские буквы. Использовался один скрытый слой из 100 нейронов с сигмоиндной функцией активации, на выходе softmax слой, а минимизировалась перекрестная энтропия. Итого легко подсчитать что всего в сети 100 * (29*29 + 1) + 26 * (100 + 1) = 86826 весов (учитывая смещения). Начальные значения весов были взяты из равномерного распределения . Во всех трех экспериментах использовалась одна и та же инициализация весов. Так же используется полный батч.
Первый
В этом эксперименте использовался простое, легкообобщаемое множество; значение скорости обучения (глобальная скорость) равняется 0.01. Рассмотри зависимость значения ошибки сети на данных, от эпохи обучения.
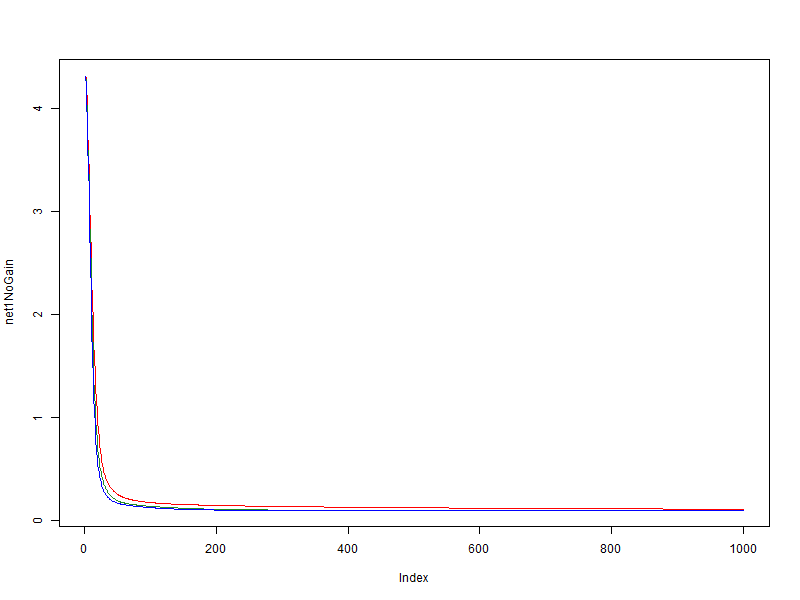
- красный — без использования модификатора
- зеленый — bonus = 0.05, penalty = 0.95, limit = [0.1, 10]
- синий — bonus = 0.1, penalty = 0.9, limit = [0.01, 100]
Видно что на очень простом множестве положительный эффект модификатора есть, но он не велик.
Второй
В противовес первому эксперименту, я взял множество, которое я уже как то обучал. Я был заранее в курсе что при скорости обучения 0.01, осцилляция значения функции ошибки начинается очень быстро, а при более меньшем значении множество обобщается. Но в данном тесте будет использоваться именно 0.01, т.к. хочется посмотреть что произойдет.
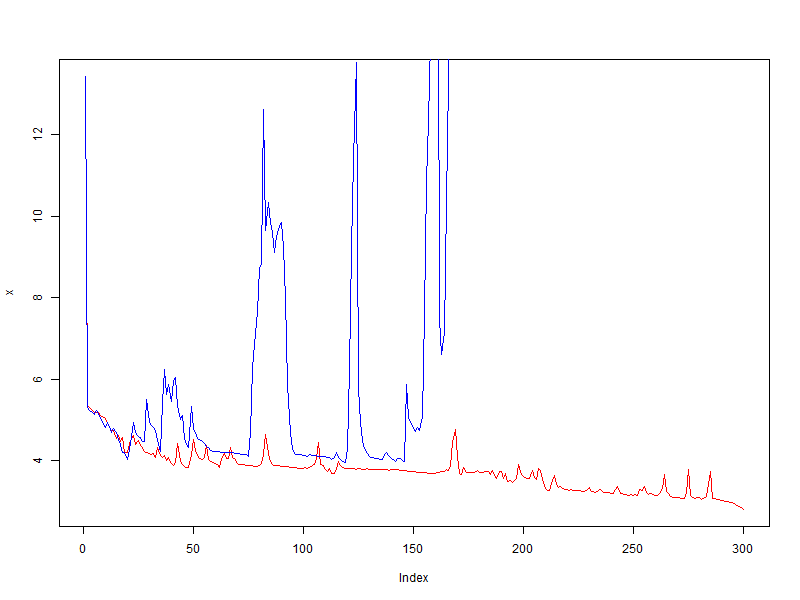
- красный — без использования модификатора
- синий — bonus = 0.05, penalty = 0.95, limit = [0.1, 10]
Полный провал! Модификатор не только не улучшил качество, а напротив, он усилил осцилляцию, в то время как без модификатора, ошибка в среднем падает.
Третий
В этом эксперименте я использую то же множество, что и во втором, но глобальная скорость обучения равна 0.001.
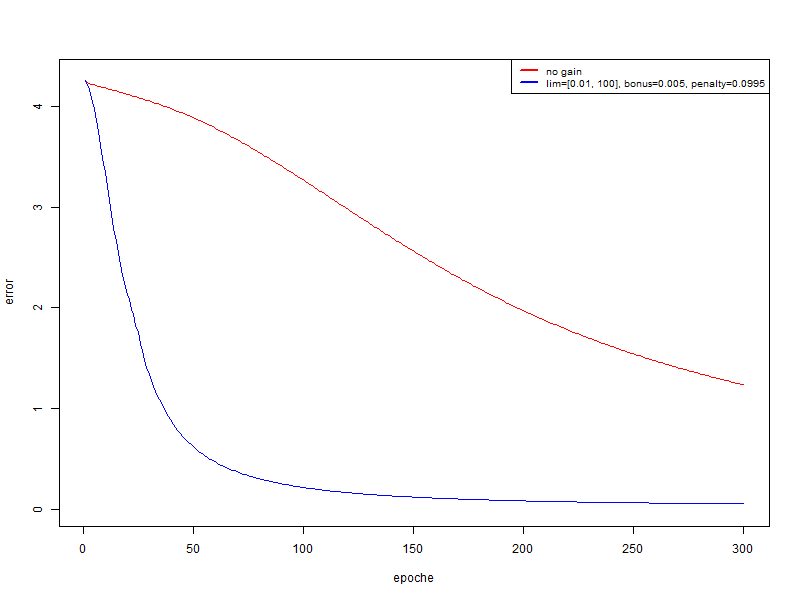
- красный — без использования модификатора
- синий — bonus = 0.005, penalty = 0.995, limit = [0.01, 100]
В данном случае мы получаем очень существенный прирост к качеству. И если после 300 эпох прогнать распознавание на обучающем множестве и тестовом:
- красный: на обучающем множестве 94.74%, на тестовом 67.18%
- синий: на обучающем множестве 100%; на тестовом 74.4%
Вывод
А вывод я для себя сделал один, что этот способ не является заменой выбора глобальной скорости обучения, но является хорошим дополнением к уже подобранной скорости обучения.
Автор: mephistopheies
