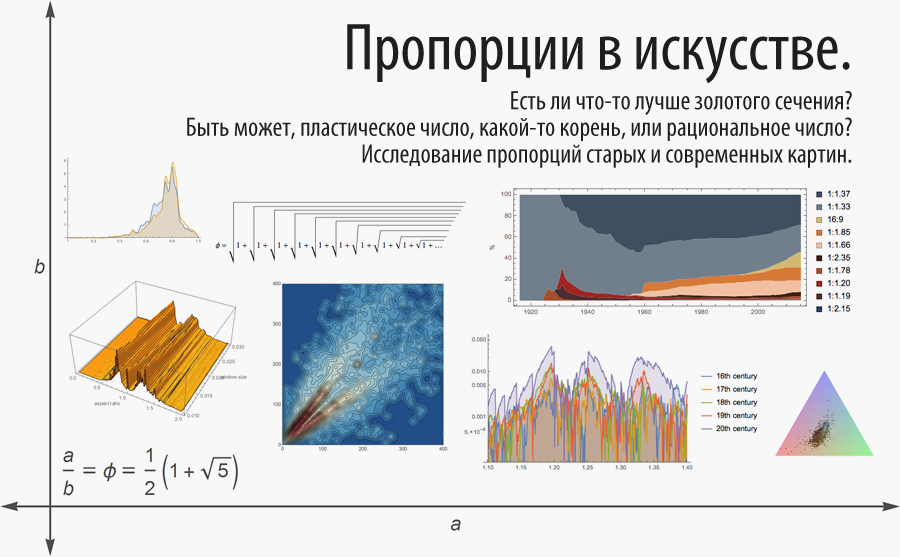
Перевод поста Майкла Тротта (Michael Trott) "Aspect Ratios in Art: What Is Better Than Being Golden? Being Plastic, Rooted, or Just Rational? Investigating Aspect Ratios of Old vs. Modern Paintings".
Код, приведенный в статье, можно скачать здесь.
Выражаю огромную благодарность Кириллу Гузенко KirillGuzenko за помощь в переводе и подготовке публикации
Содержание
Предисловие: золотое сечение — красивая математическая концепция
Работа Фехнера 1876 года об эстетичности прямоугольников и соотношениях сторон в картинах
Легкий старт: анализ «Artwork» — области базы знаний Wolfram Knowledgebase
Первая часть: особенности вероятностного распределения соотношений сторон
Соотношения сторон для разных веков, жанров и художников
Анализируя пять старых немецких музейных каталогов
Коллекция Кресса: четыре больших PDF файла
У нас представлены коллекции следующих галерей: Метрополитен (Metropolitan), институт искусств Чикаго, Эрмитаж, Национальная Галерея (National Gallery), Рейксмюзеум (Rijks) и Тейт Британия
Исключение в соотношениях сторон: Национальная портретная галерея
Веб-галерея изящных искусств: удобная база данных, готовая к использованию
Примечание II: важность точности в измерениях
WikiArt: еще один крупный веб-ресурс
Коллекция Французского государственного музея
Картины в итальянских церквях: высота есть всё
Смитсоновская коллекция
Большая коллекция картин в Великобритании
Нынешний рынок изящных искусств: рациональней чем когда-либо
Проданные картины: большинство написаны недавно, а у распределения длинный хвост
Восток: все показатели отличаются
Пропорции пакетов, автомобилей, этикеток, логотипов, эмблем, бумаги, банкнот, почтовых марок и фильмов
— Продукты из супермаркета
— Винные этикетки
— Этикетки немецких сортов пива
— Логотипы продуктов питания
— Банкноты
— Размеры автомобилей
— Бумажные листы
— Марки
— Эмблемы команд NCAA (Национальной ассоциации студенческого спорта)
— Эмблемы немецких футбольных клубов
— Форматы фильмов
Заключение: так какое соотношение самое «лучшее»?
Картины великих мастеров — едва ли не самое прекрасное из человеческого наследия. Ими дорожили и восхищались, бережно хранили и продавали за сотни миллионов долларов, и, возможно, не по случайности они являются главной целью похитителей предметов искусства. Их композиции, цвета, детали, темы могут держать нас в восхищении и внимании часами. Но что можно сказать об отношении их внешних размеров — высоты к ширине?
В 1876 году немецкий ученый Густав Теодор Фехнер изучал человеческое восприятие прямоугольных форм, а после заключил, что прямоугольники с золотой пропорцией (то же, что и золотое сечение) наиболее приятны для человеческого глаза. Чтобы проверить свои экспериментальные наблюдения, Фехнер также проанализировал соотношения более десяти тысяч картин.
Немного больше узнать о Фехнере нам поможет следующий код:
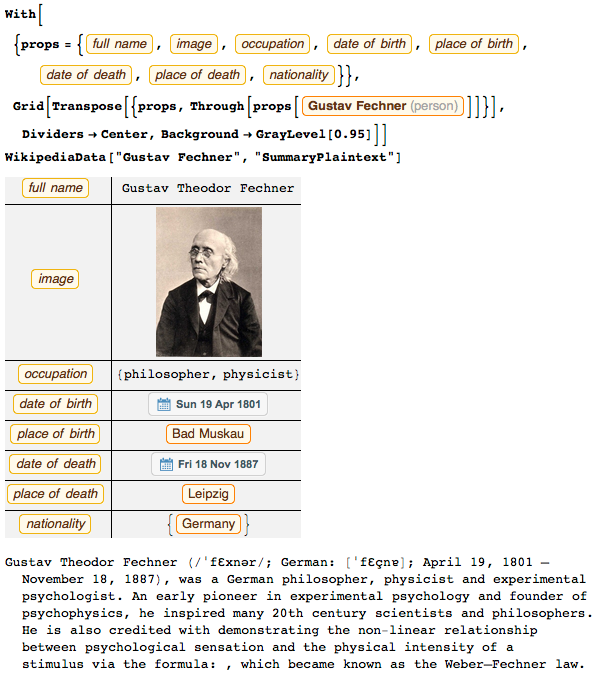
По меркам 1876 года Фехнер проделал удивительную работу, и мы можем повторить некоторые фрагменты его аналитической работы, используя возможности современного информационно насыщенного мира — с технологиями больших данных, инфографикой, численными моделями, системами знаний научного и цифрового миров.
После обзора золотой пропорции и выводов Фехнера, мы рассмотрим соотношения сторон в различных группах картин и итоговое распределение, а также наиболее популярные соотношения. Мы узнаем о тенденциях последнего столетия в области соотношений сторон и рассмотрим то, как оно стало более рационалистическим.
Предисловие: золотое сечение — красивая математическая концепция
Золотое сечение φ = (1+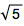 
) /2≈1.618033988… — особое число в математике. В двоичной или десятичной форме последовательность его чисел выглядит более или менее случайной:
Его представление в виде цепной дроби столь же лаконично и красиво, сколь и получаемое математическое выражение:
Можно записать его в более явной форме:
Другим схожим представлением является подобная итерация квадратного корня:
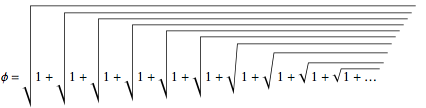
Хотя это и простые квадратные корни, однако золотое сечение — особенное число. Например, это самое плохо приближаемое иррациональное число:
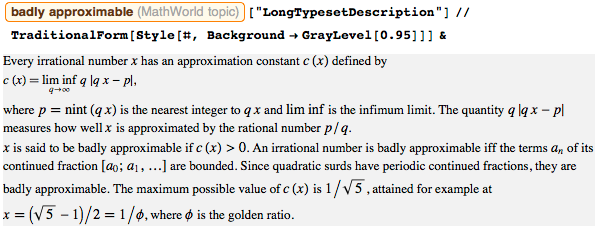
Вот график, показывающий последовательность q ∙ |q ∙ ϕ – round(q ∙ ϕ)|. Значение членов последовательности всегда больше, чем 1/5^½:
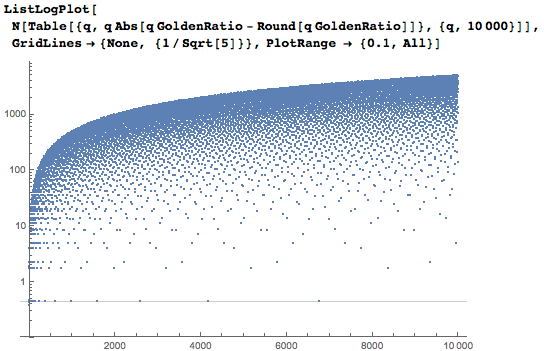
Кроме того, мы можем показать приближения к золотому сечению, беря последовательные части цепной дроби:
Визуализация определяющего золотого сечения уравнения 1 + 1 / φ = φ показана ниже. Оно задает отношение показанных отрезков (красный отрезок имеет длину 1 / φ, синий — 1).
Ниже представлены широкий и высокий прямоугольники с соотношениями сторон, равными золотому сечению и 1/золотое сечение соответственно.
И не удивительно, что столь красивое с точки зрения математики число часто использовалось для создания эстетичных форм. История золотого сечения уходит в глубину веков. Оно было математически описано ещё Евклидом, и знаменитые рисунки да Винчи были основаны на золотом сечении.
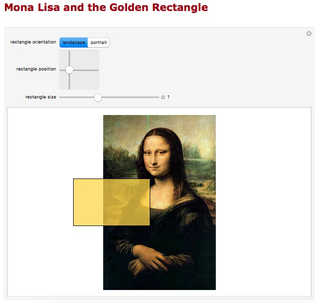
На сайте Wolfram Demonstrations Project имеется около девяноста интерактивных документов, завязанных на использование золотого сечения. Особенно стоит обратить внимание на Мону Лизу и золотой прямоугольник, а так же на золотую спираль.
Золотое сечение часто встречается в природе. Версия золотого сечения для углов есть так называемый золотой угол, который разбивает окружность на две части, длины которых имеют отношение, равное золотому сечению:
Золотой угол, к примеру, можно встретить в филлотаксисных моделях:
В работе M. Akhtaruzzaman and A. Shafie приводится очень длинный список того, где в природе и рукотворных объектах встречается золотое сечение.
Тем не менее, универсальность золотого сечения в искусстве часто переоценивается. Самые популярные заблуждения приведены в работе за авторством Markowsky.
В дальнейшем мы часто будем сталкиваться с квадратным корнем из золотого сечения. Если рассматривать и комплексные числа, то другая, достаточно простая цепная дробь даст квадратный корень из золотого сечения в составе своей действительной и мнимой части (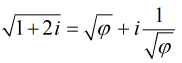
— прим. ред.):
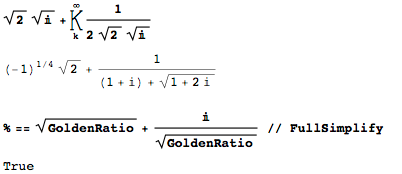
Сам термин золотое сечение впервые был использован Мартином Омом — братом известного физика Георга Ома — в своей книге в 1835 году.
Работа Фехнера 1876 года об эстетичности прямоугольников и соотношениях сторон в картинах
В первом томе часто цитируемой работы Vorschule der Aesthetik (1876), Густава Теодора Фехнера — физика, психолога-экспериментатора и философа — обсуждается восприятие человеком золотого сечения.
В наши дни Фехнер, вероятно, наиболее известен законом о субъективности в восприятии ощущений (интенсивность ощущения прямо пропорциональна логарифму интенсивности раздражителя), который носит название закон Вебера-Фехнера:
В главе 14.3 (том 1) своей книги Фехнер рассуждает об эстетике в соотношениях сторон прямоугольников. Опросив 347 человек, каждому из которых было предложено на выбор 10 прямоугольников с различными соотношениями сторон, самым популярным оказался с соотношением сторон 34/21, и это соотношение отличается от золотого сечения менее чем на 0,1%. Ниже представлена цитируемая по сей день, однако редко встречающаяся в изданиях, таблица с результатами Фехнера:
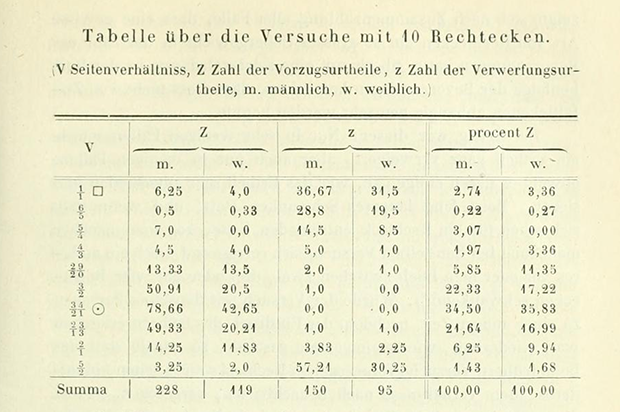
В 33 главе второго тома обсуждаются размеры картин, в главе 44 приводится подробный анализ (на 41 страницу) 10 558 картин из 22 европейских галерей. Занятно получилось — Фехнер обнаружил, что типичное отношение высоты и ширины для живописи сильно отклоняется от ожидаемого золотого сечения.
Фехнер провёл детальный анализ 775 картин на охотничью и военную тематику, и более грубый анализ для оставшихся 9 783 картин. Ниже представлены результаты для картин на охотничью и военную тематику (Genre), пейзажей (Landschaft) и натюрмортов (Stillleben). В таблице высота обозначается как h, а ширина как b. А V.-M. есть соотношение h/b или b/h:
И вот, в наши дни, мы можем повторить его анализ, используя современные средства и знания.
Более подробно ознакомиться с изменёнными версиями эксперимента Фехнера помогут работы McManus (тут и тут), McManus et al., Konecni, Bachmann, Stieger и Swami, Friedenberg, Ohta, Russel, Green, Davis and Jahnke, Phillips et al. и Höge. Jensen недавно проанализировал картины из базы CGFA, но используемые дискретные значения высоты и ширины (из анализа количества пикселей в изображениях) не позволяют получить крупномасштабную структуру распределения соотношений сторон, и тем более получить явные экстремумы (ниже будет приведен анализ тестового множества изображений).
В то время как Фехнер сделал подробный анализ количественных инвариантов (средние значения, медианы и прочее) для соотношений сторон картин, он не исследовал общую форму распределения соотношений сторон, равно как и распределение локальных максимумов в этом распределении.
Легкий старт: анализ «Artwork» — области базы знаний Wolfram Knowledgebase
Одной из предметных областей функции EntityValue является "Artwork" (предметы искусства). Здесь мы можем получить названия работ, имена художников, даты окончаний работ над картинами, а также значения ширины и высоты нескольких тысяч картин. Картины доступны как класс объектов из области "Artwork" в Wolfram Knowledgebase (базе знаний Wolfram):
Вот типичный пример получаемых данных:
Картины имеют самое разнообразное соотношение сторон — имеются как очень широкие, так и весьма вытянутые вертикально. Ниже представлен коллаж из 36 изображений картин, отсортированных по их соотношению сторон (отношение ширины к высоте). Каждое изображение представляется в сером квадрате с красной каймой:
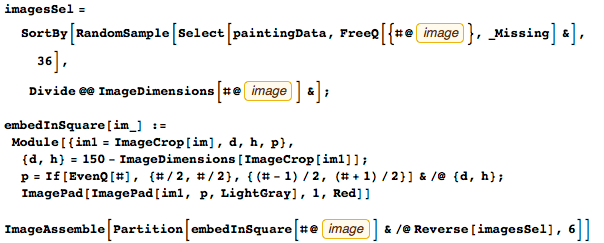
Большинство картин имеют соотношение сторон в диапазоне от 1/4 до 4. Вот примеры весьма вытянутых по ширине или высоте картин:
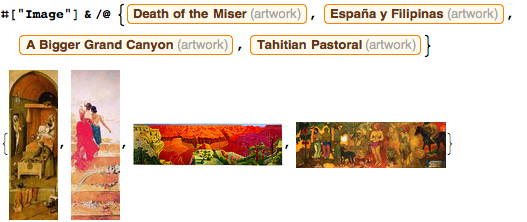
Мы можем получить представление о наиболее распространенных тематиках картин, составив из них облако слов:
Теперь, когда мы загрузили все изображения, давайте их исследуем. Можно взять средние значения всех цветов для каждой картины и разместить их на цветовом треугольнике RGB:
Прежде чем анализировать пропорции h/b более подробно, давайте рассмотрим их произведение, что даст нам площадь картины. (В упомянутой выше работе Фехнера много внимания уделялось этому вопросу.)
Разместим теперь все картины на плоскости (по горизонтали — соотношение сторон, по вертикали — площадь картины). Так как размеры картин сильно варьируются, мы будем использовать логарифмическую шкалу по вертикали. Добавим также всплывающие подсказки, которые будут показывать картину и её параметры для каждой из точек:
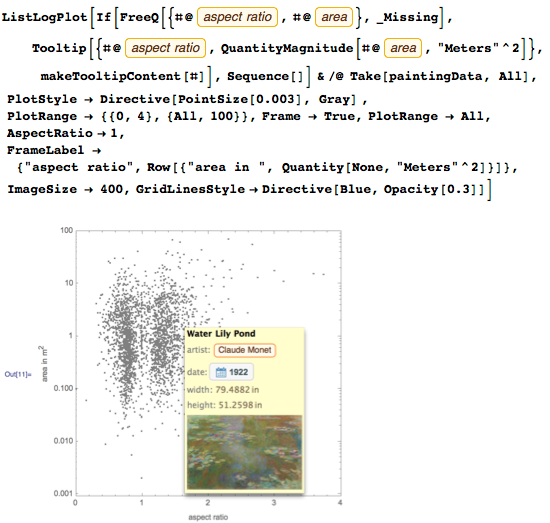
Ниже представлена гистограмма распределения соотношений сторон.
Начиная с этого момента, следуя определению в Wolfram Language, будем считать, что
соотношение сторон = высота / ширина,
а не наоборот. Как было показано выше, Фехнер придерживался такого же определения.
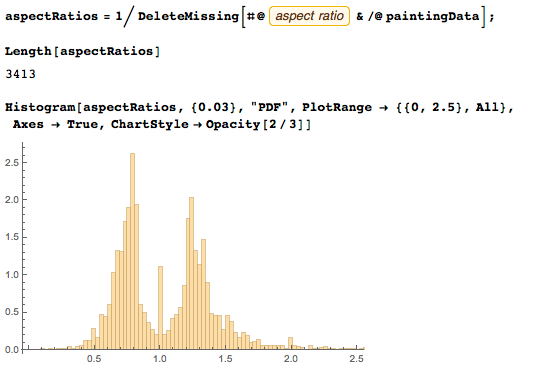
Давайте теперь рассмотрим гистограмму соотношений сторон более подробно. По форме этого распределения можно сказать, что оно тримодальное. Для широких картин (ширина > высоты) соотношение будет меньше единицы, для квадратных картин соотношение будет около единицы, а для высоких картин (высота > ширины) соотношение, соответственно, больше 1. Широкие и высокие картины дают свои пики; также можно наблюдать менее выраженные локальные пики.
Не было неожиданным получить тримодальную структуру для широких, высоких и квадратных картин. В связи с этим естественным образом возникают два вопроса:
1) Каковы значения локальных пиков?
2) Какова примерная общая форма распределения (нормальное, логнормальное и т. д.)?
В 1997 году Shortess, Clarke и Shannon проанализировали 594 картины и более детально изучили окрестность точки максимума распределения. В согласии с работой Фехнера от 1876 года, локальный максимум распределения max(h/b, b/h) лежит в точке 1.3. Число 1.3 явно отличается от золотого сечения и авторы предполагают, что, вероятно, значением этого максимума является либо число Пифагора (4/3), либо пластическое число (пластическая константа, серебряное сечение).
Пластическое число есть положительное действительное решение уравнения x³ – х – 1 = 0:
Пластическую постоянную ввёл Dom Hans van der Laan в 1928 году в качестве специального числа в контексте эстетичности трёхмерных (но не двумерных) форм. Представленная в радикалах, пластическая постоянная ℘ имеет довольно сложный вид:
«Качество» графика, полученного на основе анализа 594 картин, оказалось недостаточно, чтобы различить ℘ и 4/3, в результате чего Shortess, Clarke и Shannon предположили, что максимум соотношения сторон лежит в "платиновой константе" (введённый ими термин), значение которой приблизительно равняется 1.3. В их работе так же не были обнаружены какие-либо мелкие детали структуры графика распределения соотношения сторон.
Примечание: эта «платиновая константа» не имеет отношения к платиновому сечению, которое используется в численном анализе.
(Существует интересная математическая зависимость между золотым сечением и пластической постоянной: золотое сечение является точкой наименьшего скопления чисел Пизо, а пластическая постоянная есть наименьшее из чисел Пизо, но мы в дальнейшем не будем касаться этой связи).
Если мы уменьшим ширину прямоугольников гистограммы, то сможем увидеть по крайней мере по два максимума для широких и высоких картин:
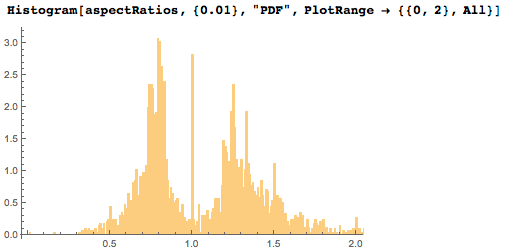
Если мы рассмотрим интегральную функцию распределения, то сможем заметить, что число квадратных картин довольно мало. Квадратным картинам соответствует небольшой вертикальный скачок при соотношении сторон, равным единице:
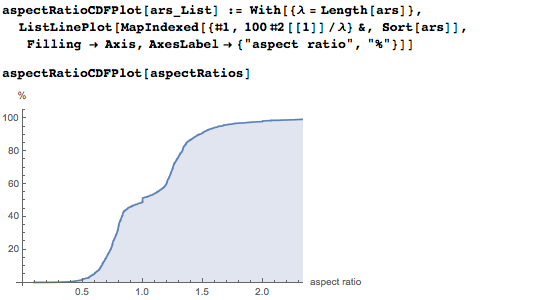
Давайте теперь сравним распределения соотношений сторон высоких и широких картин; для этого инвертируем соотношения «высоких» и совместим с «широкими». Очень хорошо совмещаются максимумы в точках 0.8 (глобальный) и 0.75 (второй максимум):
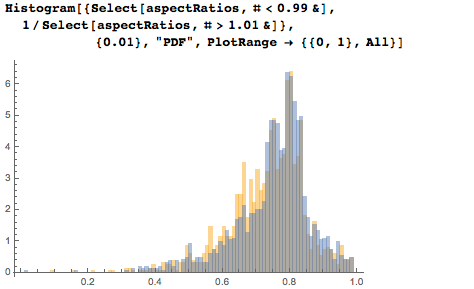
Вот как соотносятся сглаженные распределения и максимумы соотношений сторон широких и инвертированных высоких картин:
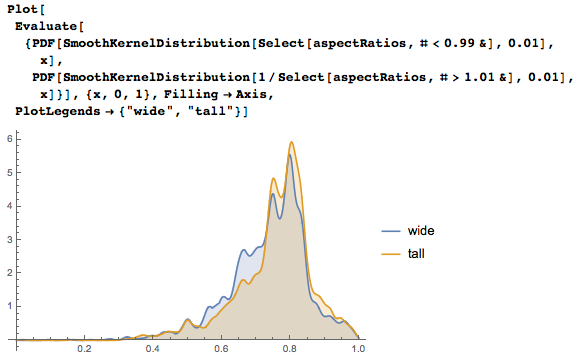
Квантильный график ниже иллюстрирует сходство наших распределений:
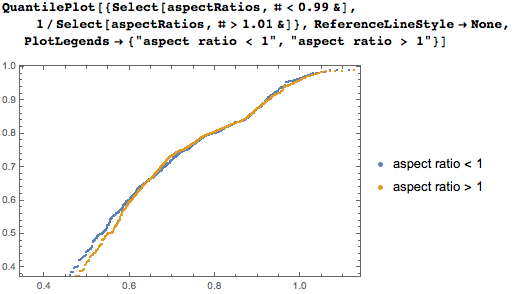
Можно ли получить максимумы в численной форме и ассоциировать их с какими-то конкретными числами? Ниже приведены вышеупомянутые константы и еще три дополнительные: квадратный корень из золотого сечения, 5/4 и 6/5:
Из всех возможных констант мы выбрали квадратный корень из золотого сечения по той причине, что она естественным образом появляется в так называемом треугольнике Кеплера. Соотношение его сторон равно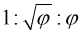 
:
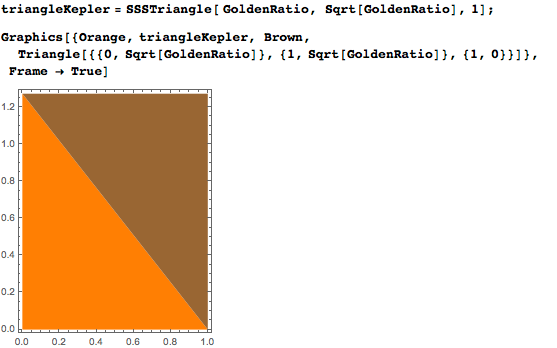
Теорема Пифагора не менее важна для квадратного корня из золотого сечения. Треугольник Кеплера становится определяющим уравнением для золотого сечения:
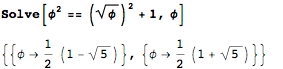
Shortess и другие включали дробь 4/3 как пифагорейскую постоянную, поскольку это число является отношением двух наименьших сторон пифагорова треугольника с длинами сторон 3, 4, 5 (3² + 4² = 5²).
А дробь 6/5 была включена потому, что, как мы увидем в дальнейшем, это соотношение сторон часто встречается в картинах за последние 200 лет.
Распределение соотношений сторон в картинах вместе с выбранными константами показывает, что наибольший пик, вероятно, лежит в значении корня из золотого сечения, а меньший пик — где-то в диапазоне 1.32… 1.33.
Вот список констант-претендентов на точное значение максимума. Мы используем этот список при дальнейшем анализе соотношений сторон в различных группах картин. Давайте проиллюстрируем эти соотношения:
На графике ниже показаны шесть констант, расположенных на числовой прямой. Разница между пластической постоянной и 4/3 является наименьшей среди всех пар из шести выбранных констант:
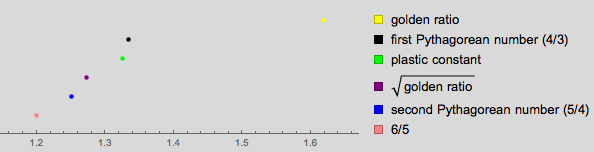
Ниже представлены широкие прямоугольники с соотношениями сторон выбранных постояннных:
Для большей наглядности разместим эти прямоугольники один над другим:
А вот приведённый выше график с отмеченными на горизонтальной оси константами:
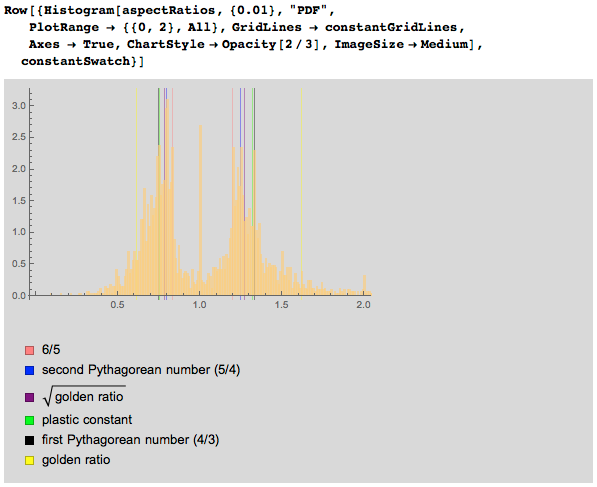
Прочие дроби с малыми знаменателями будут встречаться в различных группах картин далее, и включаться они могут согласно своим эстетическим критериям, как, к примеру, 55/45 = 11/9 = 1.(2) (см. тут, тут, тут и тут) или 27/20 = 1.35, или так называемое «мета-золотое сечение чи» — решение уравнения Χ² – Х / φ = 1 со значением 1.35…
Так как разрешение гистограммы довольно-таки ограничено, давайте подсчитаем количество картин, которые имеют определенное соотношение сторон плюс или минус небольшое отклонение. Мы можем это сделать достаточно эффективно с помощью функции Nearest:
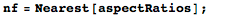
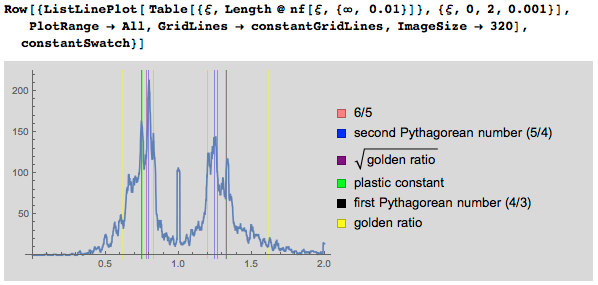
Как мы видим, можно явно различить два максимума, больший из которых ближе к квадратному корню из золотого сечения, нежели к пластической постоянной или числу Пифагора:
Первая часть: особенности вероятностного распределения соотношений сторон
Прежде чем включить в исследование большее количество художников и картин, давайте более внимательно рассмотрим распределение соотношений сторон.
Все наиболее употребимые средние значения соотношений сторон «высоких» картин больше значения соотношения сторон, на который приходится максимум:
Вот средние для «широких» картин:
Как соотносятся широкие картины с высокими? Интересно получается — их количество практически полностью совпадает:
Статистики для всех картин, рассмотренных в качестве прямоугольников (то есть соотношения сторон максимум(высота, ширина) / минимум(высота, ширина)) имеют средние, которые весьма близки к значениям для высоких картин:
Как и в рассмотренном выше графике с наложенными друг на друга распределениями, распределение высоких картин почти полностью совпадает с распределением для широких картин, в котором инвертированы пропорции. Но какое на самом деле распределение для высоких (или для всех) картин (см. вопрос 2 выше)? Если мы сгладим наше распределение, проигнорируем многочисленные малые пики и будем использовать меньшее разрешение, мы могли бы попробовать сравнить наше распределение с нормальным, логнормальным, с тяжелым хвостом (heavy-tailed distribution) и пр.
Чтобы избежать излишних шумов и артефактов, будем рассматривать лишь те картины, соотношение сторон которых меньше, чем 4:
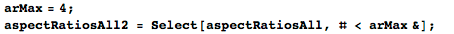
Функция SmoothKernelDistribution позволяет сгладить несколько максимумов и получить плавное распределение (график слева). Построенные в логарифмических (log-log) координатах функция риска(f(a)/(1-F(a))) и функция 1/а дают нам намёк на то, что распределение с тяжелым хвостом есть наилучшее приближение:
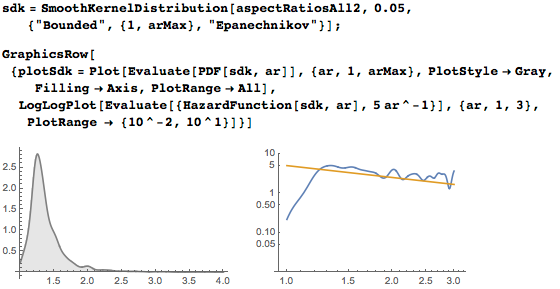
Посмотрим, как можно подогнать (fit) наше распределение под нормальное и логнормальное:
А вот распределения с тяжелым хвостом:
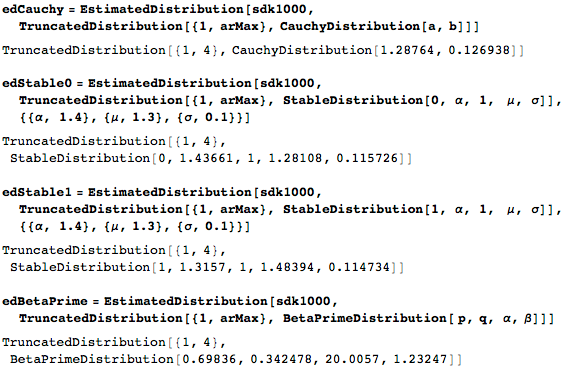
Так как соотношение высота/ширина имеет медленно убывающий хвост, нормальное, логнормальное и экстремальное распределения (extreme value distribution) являются плохими моделями. Диапазон соотношений сторон между 1.4 и 2 явно на это указывает:
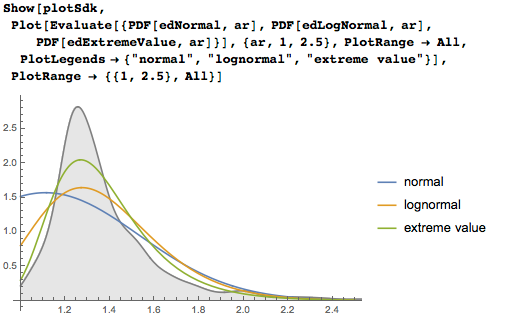
Четыре распределения с медленно убывающими хвостами в целом значительно лучше описывают наше распределение:
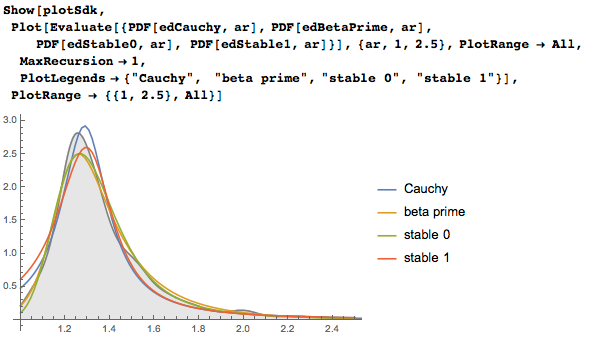
Если мы количественно оценим наши модели с использованием логарифмической меры сходства, то увидим, что усеченное распределение с тяжелым хвостом подходит лучше всего:
Распределение соотношения сторон имеет любопытное свойство: выше мы видели, что распределения широких и высоких картин после соответствующего преобразования очень близки по форме. Это означает, что их максимумы согласуются, по крайней мере, приблизительно. Но совмещение распределения p(x) высоких картин с 0 < x <1 и p̅(x) широких картин при 1 < x < ∞, даст нам, что p̅(x) = p(1/x)/x². Но в то же время для максимумов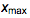 
от p(x) и 
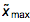от p̅(x) имеет место соотношение 
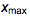≈1/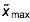
. Интересно, что для параметров, найденных для подходящих моделей распределений это свойство выполняется с точностью в 2%. В коде ниже мы получаем различие в положении максимумов для бета-простого распределения (beta prime distribution) (результаты для устойчивых распределений почти одинаковы).
Соотношения сторон для разных веков, жанров и художников
Теперь перед нами встает вопрос: как наше тримодальное распределение менялось во времени, от жанра к жанру, в зависимости от художников?
Давайте рассмотрим зависимость от времени, сгруппировав картины по векам (считаются года окончания работы над картиной). Можно заметить, что по крайней мере с четырнадцатого века, высокие картины зачастую имели соотношение сторон около 1.3, широкие картины имели соотношение сторон около 0.76, а квадратные картины стали популярны лишь сравнительно недавно. Также можно увидеть, что для высоких картин распределение имеет более плоскую форму в шестнадцатом, семнадцатом и восемнадцатом веках, если сравнивать с распределением для девятнадцатого века (мы увидим аналогичные тенденции в других подборках картин):
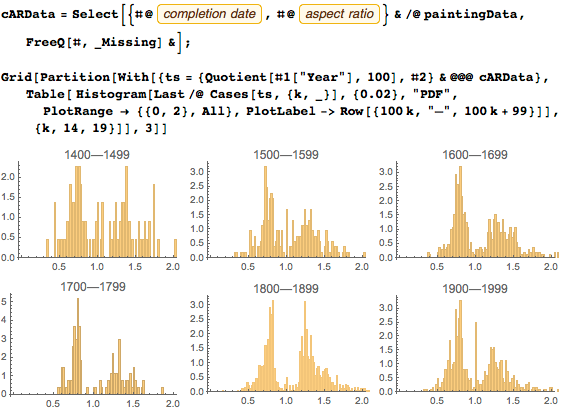
Медиана соотношений сторон всех картин снизилась за последние 500 лет и стала равна чуть более, чем 1.3. (здесь мы определяем соотношение сторон как отношение длины более вытянутой стороны к меньшей стороне). Среднее также снизилось и, кажется, зафиксировалось в районе 1.35:
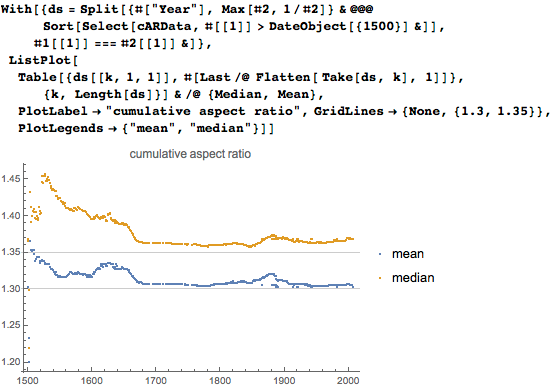
Для сравнения, вот распределение площадей картин (в квадратных метрах) и то, как оно менялось на протяжении веков:
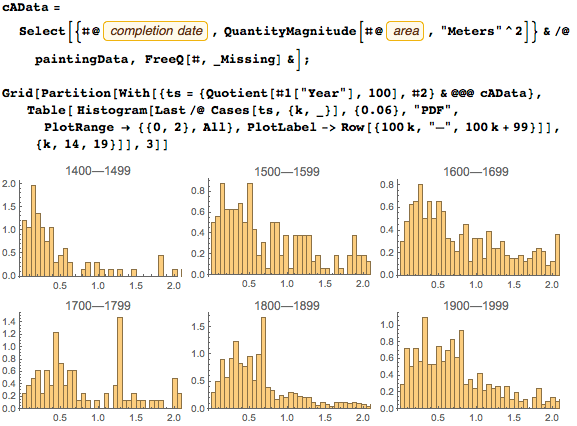
Последние 450 лет медиана площади картин была весьма стабильной и равнялась примерно 2 м2:
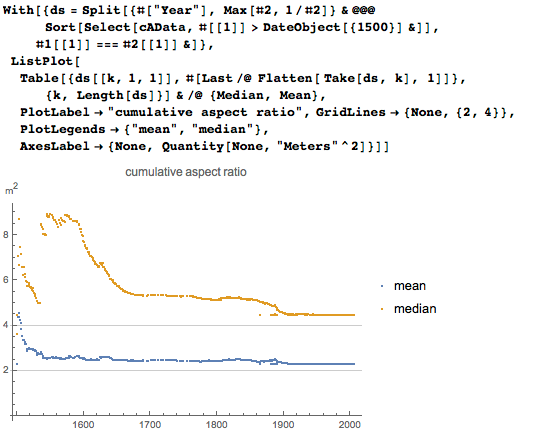
А что можно сказать о соотношениях в различных художественных течениях? WikiGallery содержит весьма наглядную информацию о направлениях в изобразительном искусстве. Мы импортируем страницу и получим список направлений, а так же то, сколько картин в каждом из них представлено:
К сожалению, информация о размерах доступна не для всех картин. Импорт всех страниц с картинами и извлечение данных по высоте и ширине из размера миниатюр позволяет строить с той или иной точностью распределения пропорций для каждого стиля или жанра.
Подавляющее большинство направлений демонстрируют выраженные бимодальные распределения с пиками в соотношениях сторон около 1.3 и 0.76 (направления сортируются по общему количеству картин, представленных на соответствующих страницах Wiki).
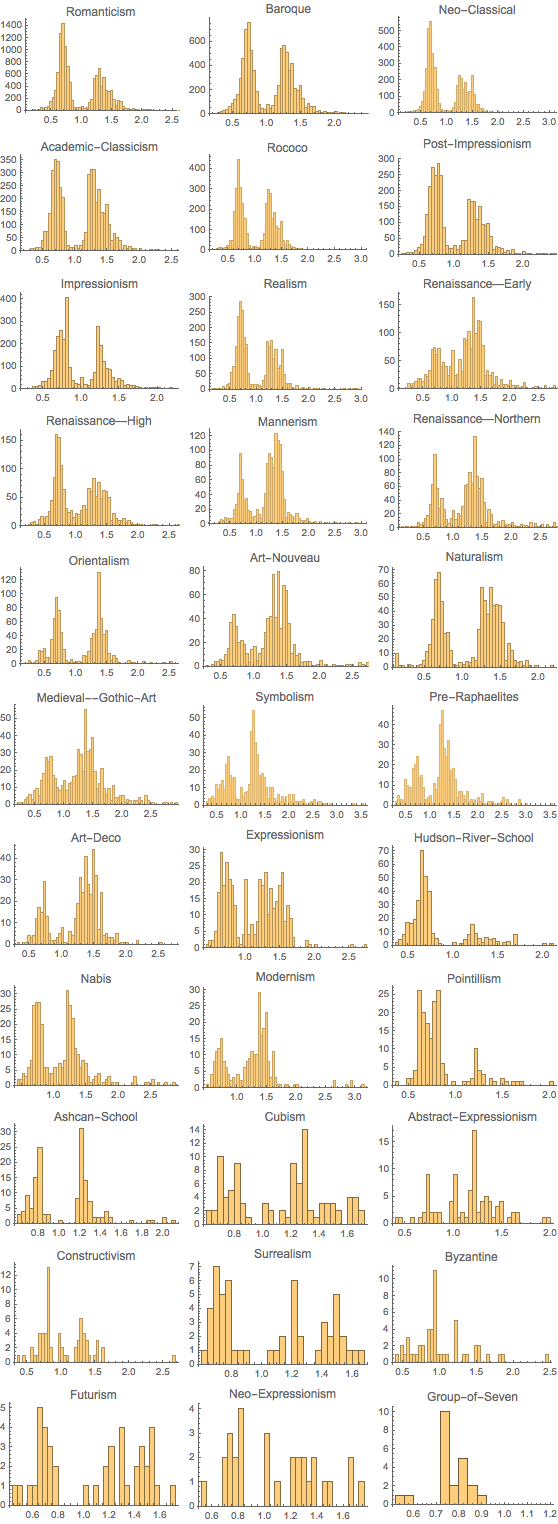
Давайте снова задействуем Википедию и рассмотрим соотношения сторон у различных художников:
И пусть общее количество картин на гистограмму теперь значительно меньше, мы всё равно можем обнаружить бимодальную (для квадратных картин пик пропал) форму распределения. И снова можно заметить выраженные максимумы в точках 1.3 для высоких и 0.76 для широких картин.
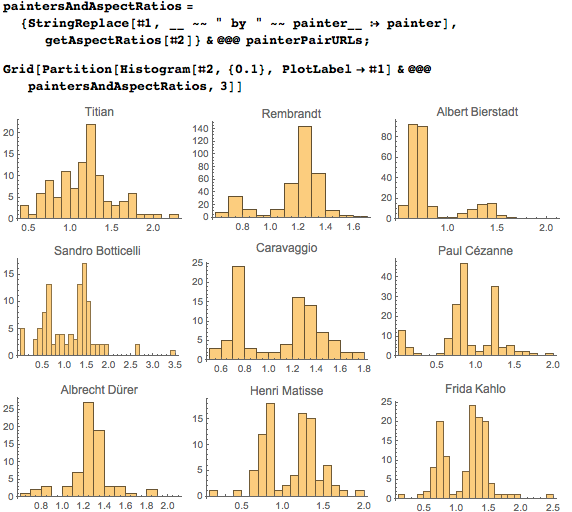
Опять-таки распределения содержат острые пики. Некоторые художники, такие как Сезанн, предпочитали стандартные размеры холста (для более подробного исследования размеров холста, которые использовал Фрэнсис Бэкон, см. здесь).
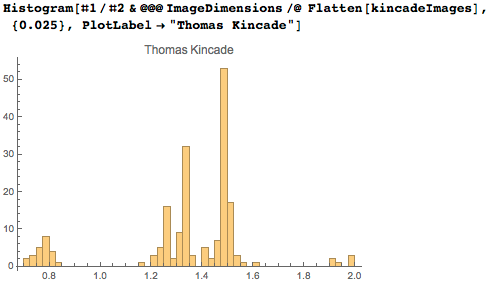
Давайте также рассмотрим более современного художника — Томаса Кинкейда, «художника света». Современные картины используют стандартные материалы и реализуются в определённых размерах и соотношениях сторон, так что форма и размер картины по большей части определяются стандартами, нежели эстетикой. Потому на этот раз мы будем ориентироваться не на текстовые данные об изображении, а на сами изображения, получая данные об их размерах исходя из их пиксельного разрешения. Даже если использовать миниатюры, распределение соотношений сторон будет вполне корректным:
В дополнение к нашему типичному максимуму ~1.3, можем наблюдать выраженный максимум около 3/2 — весьма вероятно, это артефакт стандартизации:
Анализируя пять старых немецких музейных каталогов
Приведенные выше гистограммы показывают, по крайней мере два максимума для высоких картин, а также два максимума для широких картин, с большим пиком рядом с квадратным корнем из золотого сечения. Поскольку мы не знаем, каковы были критерии отбора для художественных работ, включенных в «Artwork» — области Entity, — мы должны проверить нашу гипотезу на некоторых независимых подборках картин.
Доступным источником по размерам картин являются музейные каталоги. Различные старые каталоги, похожие на те, которыми пользовался Фехнер, доступны в отсканированных и распознанных формах. Вот примеры:
- Beschreibendes Verzeichnis der Gemälde im Kaiser Friedrich-Museum, 1906
- Katalog der Gemälde-Sammlung der Kgl. Älteren Pinakothek in München, 1886
- Verzeichnis der Gemälde-Sammlung im Kgl. Museum der bildenden Künste zu Stuttgart, 1891
- Katalog der Königlichen Gemäldegalerie zu Dresden, 1896
- Katalog der Königlichen Gemäldegalerie zu Cassel, 1913
Мы просто импортируем из каталогов тестовые распознанные версии. В различных каталогах длина и ширина картин могут представляться по разному, однако в пределах одного каталога обычно эти параметры содержатся в одном виде. В результате, посмотрев на то, в какой форме представляются данные, не представляется сложной задачей извлечь данные о размерах с помощью строковых шаблонов.
Каталог музея Кайзера Фридриха (ныне Музей Боде):
Каталог из Пинакотеки в Мюнхене (ныне Старая Пинакотека):
Каталог из музея der bildenden Künste zu Stuttgart (ныне Государственная галерея Штутгарта):
Каталог из Gemäldegalerie в Дрездене (ныне Галерея старых мастеров Дрездена):
Каталог Gemäldegalerie zu Cassel (ныне Neue Galerie Kassel):
Для всех пяти музеев результаты весьма схожи:
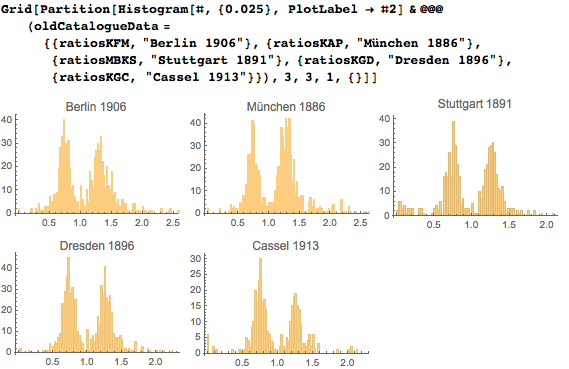
Добавим новые данные из этих пяти каталогов и построим всё это вместе константами, обозначенными вертикальными линиями:
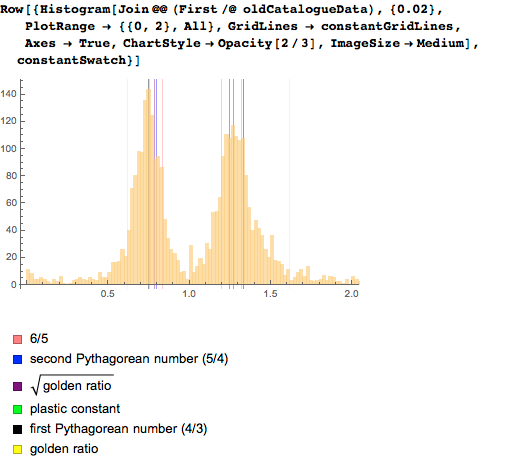
И снова мы наблюдаем два глобальных максимума в распределении соотношений сторон. Для высоких картин мы получаем довольно ровный максимум, без четко прослеживающихся локальных минимумов.
(Сайт archive.org содержит и более старые каталоги живописи, например, каталоги Schloss Schleissheim, коллекции Бертольд Захарии, коллекции Национальной галереи Баварии и многие другие. Распределения соотношений сторон картин в этих каталогах очень похожи на те, что мы сейчас анализируем).
Коллекция Кресса: четыре больших PDF файла
Известной коллекцией живописи является коллекция Кресса. Отдельные изображения находятся во многих музеях в США. Но, к счастью (для нашего анализа), данные по находящимся в каталоге картинам доступны в четырех подробных каталогах в виде PDF документов — в сумме это около 900 страниц описания картин. (Большая часть данных, анализируемых в этой статье, соответствует исключительно произведениям западного искусства. Касательно восточных предпочтений в искусстве — можно посмотреть недавнюю работу Zheng, Weidong и Xuchen).
Импортировав PDF файлы в текстовой форме и выудив оттуда значения соотношений, мы получим около 700 новых точек. (С этого момента я больше не буду приводить код импорта данных с различных сайтов; зачастую время загрузки всех данных очень велико, и повторить загрузку по-быстрому не получится).
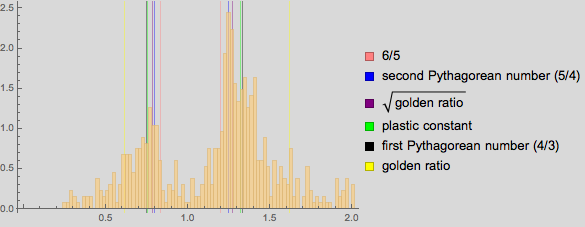
В этот раз мы наблюдаем локальные максимумы вблизи корня из двух и золотого сечения.
У нас представлены коллекции следующих галерей: Метрополитен (Metropolitan), институт искусств Чикаго, Эрмитаж, Национальная Галерея (National Gallery), Рейксмюзеум (Rijks) и Тейт Британия
Для того, чтобы удостовериться в существовании явных максимумов и их положений в распределении соотношений сторон, давайте рассмотрим эти распределения по известным мировым музеям.
Музей искусства Metropolitan имеет отличный онлайн-каталог. Задав критерий поиска для картин как «холст и масло», мы можем извлечь их пропорции.
На этот раз, глобальный максимум, кажется, немного не доходит до 1.27:
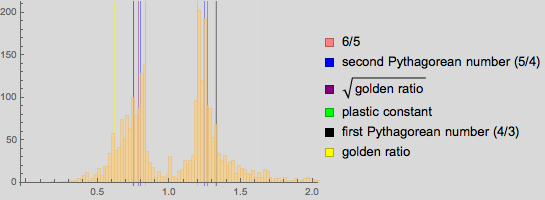
Институт искусств Чикаго имеет удобный поиск, который позволяет найти, к примеру, картины, сделанные в период с 1600 по 1800 гг. Полученные данные дают нам ещё около 1200 точек, а глобальный максимум находится очень близко к корню из золотого сечения:
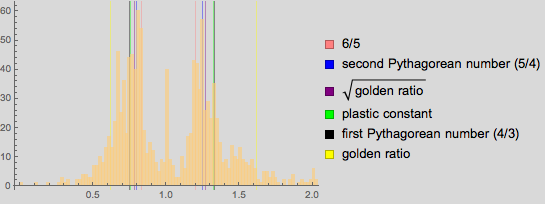
Сайт Эрмитажа весьма удобен для анализа и содержит информацию о 3400 картинах из своей коллекции. Анализ соотношений сторон снова показывает два различных максимума для высоких картин:
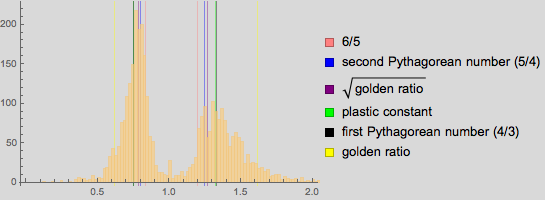
Наша четвёртая коллекция для анализа — картины из Национальной галереи. Распределение заметно отличается от предыдущих:
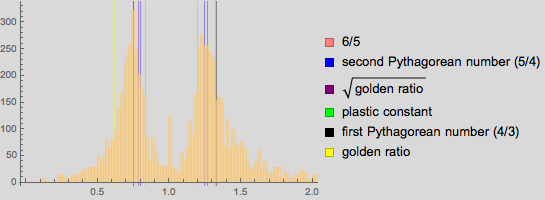
Относительно необычное распределение идет вместе со следующим распределением возраста картин. В этой коллекции мы видим максимум на картинах 16-го века, что сильно её отличает от других:
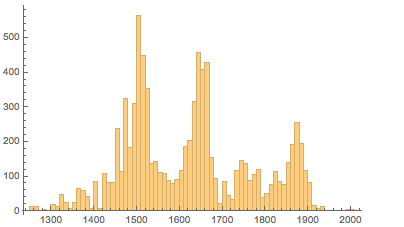
Рейксмюзеум в Амстердаме представляет еще одну обширную коллекцию старых картин. Вот распределение соотношения сторон для 4600 картин из этой коллекции:
В шестом примере рассмотрим картины из коллекции Тейта. Большая часть из 8000+ картин коллекции Тейта являются относительно новыми. Вот их распределение по годам:
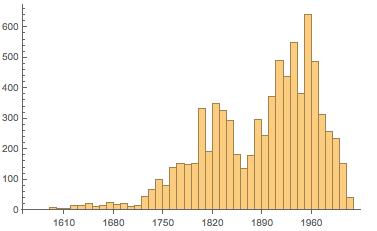
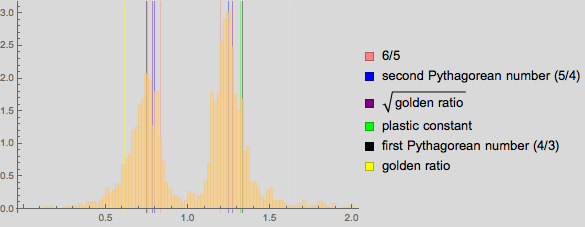
Распределение соотношений сторон весьма хорошо, но не идеально, соотносится с нашими константами:
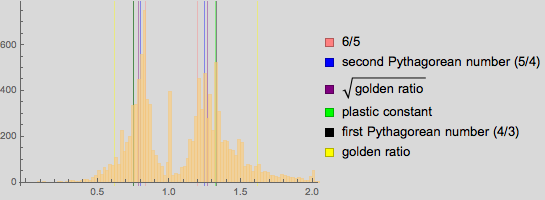
А с наложением таких дробей, как 6/5, 5/4, 9/7, 4/3 и 3/2, мы получим хорошие приближения локальных максимумов для высоких картин (тут мы используем чуть меньший размер столбца диаграммы для лучшего разрешения).
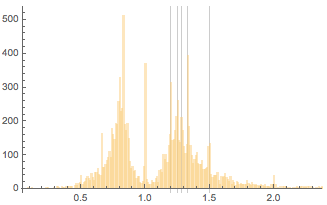
Использование основанных на Nearest решений с лучшим разрешением в пределах небольшого диапазона показывает, что максимумы ширин и высот картин лежат на рациональных числах 6/5, 5/4, 9/7, 4/3, 3/2, и их обратных (мы используем округление соотношения сторон до 0.01).
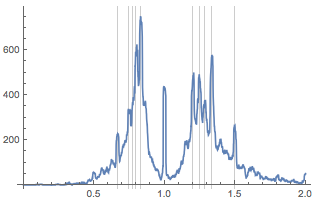
Существует небольшая зависимость в положениях пиков от размера зазора, используемого в Nearest:
Обратите внимание, что мы указывали вертикальные линии на дробях в приведенном выше графике. В пределах 1% от 9/7 мы находим квадратный корень из золотого сечения и такой дроби, как 14/11. Таким образом, решить, какое из чисел является реальным максимумом с текущими данными и точностью не представляется возможным:
Коллекцию Тейта выделяет кое-что уникальное, и это кое-что является очень важным в нашем исследовании. Вот два примера с данными по этой коллекции:
Обратите внимание на очень точные измерения размеров картин, вплоть до миллиметров. То есть этот набор данных является очень надёжным, а кривая в распределении соотношения сторон даст нам очень точные значения максимумов.
Исключение в соотношениях сторон: Национальная портретная галерея
Национальная портретная галерея содержит десятки тысяч портретов.
Не представляет сложности импортировать отдельные веб-страницы вместе с размерами:
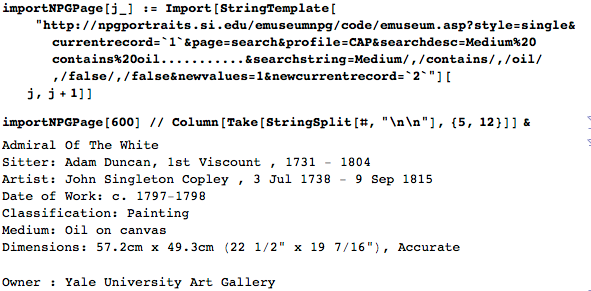
Неудивительно, что портреты имеют в среднем значительно более равномерное соотношение сторон, нежели пейзажи, картины охотничьих, военных и прочих тематик. На этот раз мы получаем значительно более унимодальное распределение. Ниже приведена гистограмма для примерно 45 000 соотношений сторон:
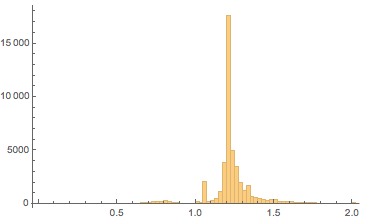
Увеличив область максимума, мы сможем увидеть, что очень большая часть имеет соотношение сторон 6/5. Второй максимум приходится на 5/4, а третий на 4/3:
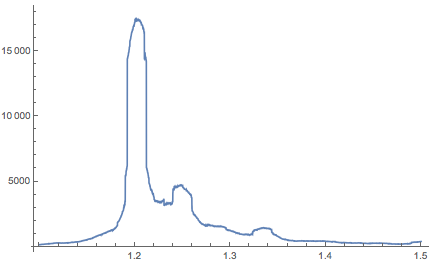
В то время как золотое сечение чаще используется для центральной части лица человека (см., например, здесь, здесь и здесь), большинство портретов изображают всю голову человека. Учитывая, что среднее соотношение высота/ширина человеческого лица (за исключением ушей и волос), равняется 1.48, наблюдаемый максимум при 1,2 не кажется неожиданным. Для более детального исследования лиц в живописи рекомендую посмотреть де ла Роса и Суарес.
Веб-галерея изящных искусств: удобная база данных, готовая к использованию
Проанализированный набор данных пока что не позволяет точно определить положение максимума. Тому есть две причины: мало картин в наборах данных и размеры картины часто недостаточно точны. Так давайте возьмем бОльший набор. Веб галерея изящных искусств — венгерский сайт, который дает возможность загрузить набор данных по картинам в виде таблицы файлом формата CSV.
Файл использует точку с запятой в качестве разделителя, так что мы должны извлекать столбцы написав свой парсер, а не с помощью Import:
Нам доступны ледующие данные:
А вот как выглядит обычная запись. Размеры в формате высота х ширина:
Большинство из приведенных произведений, к счастью, картины:
Извлекая картины с данными по размерам (не все картины содержат информацию о размерах), получаем 18 800+ точек данных:
Построив все длины и ширины из набора данных, получим следующую диаграмму:
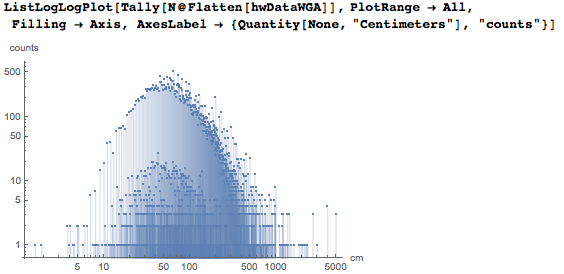
Округлив значения до одного сантиметра, мы получим следующую гистограмму для всех ширин и длин. Можно заметить многочисленные выраженные пики и дискретные длины:
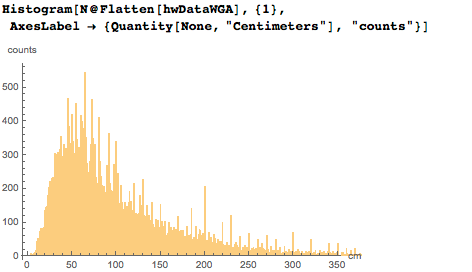
Диаграмма фактических размеров картин показывает, что многие картины менее, чем 140 см в высоту и/или ширину:
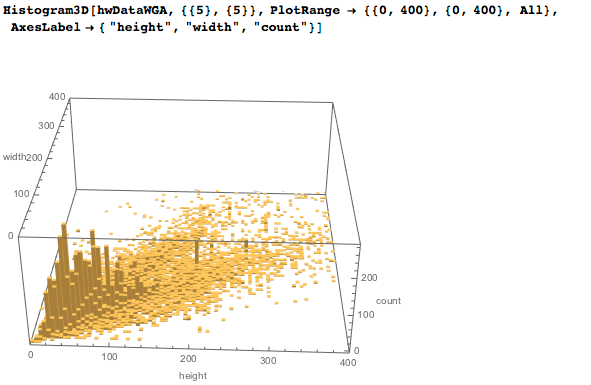
Контурный график сглаженной версии двумерного распределения плотности ширин и высот содержит два выраженных «хребта» для широких и высоких картин:
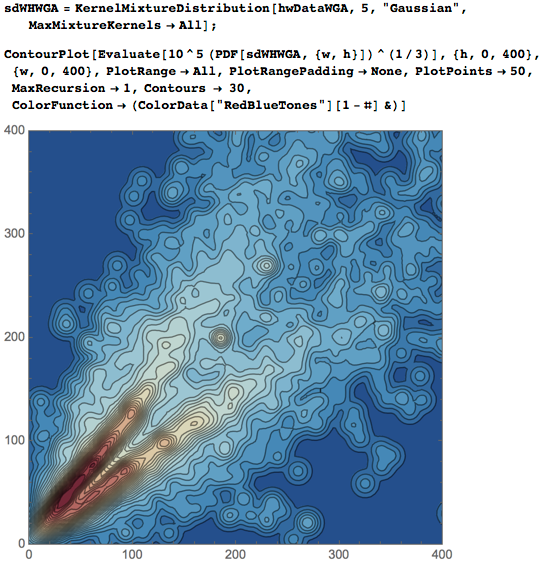
Глядя на значения длин можно заметить числа, кратные 5 см и 10 см, однако большая часть чисел не выглядит так, как будто значения после измерений округляли:
Следующая иллюстрация показывает то, как изменялись наиболее распространенные длины и ширины картин с течением времени:
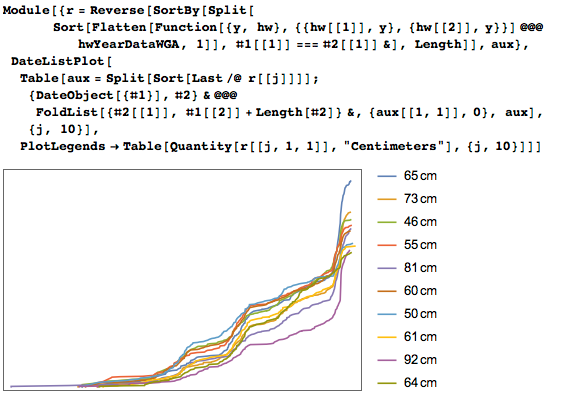
Построив ширины и высоты, отсортированные по векам, можно заметить, что многие из самых высоких пиков берут своё начало в девятнадцатом веке. (Обратите внимание на гораздо меньшую вертикальную шкалу для картин из двадцатого века.)
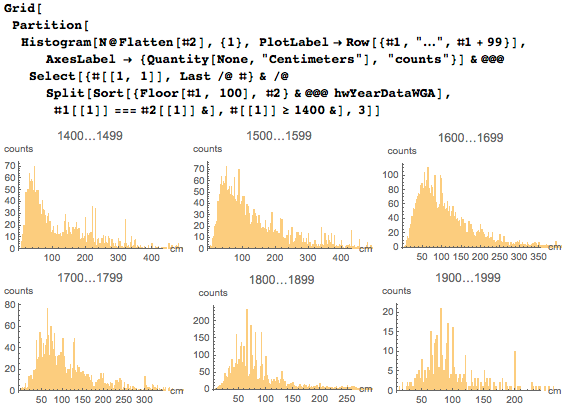
Для последующего сравнения нам понадобится получить модель распределения ширин картин. Округлим значения с точностью до 5 см для того, чтобы избавиться от локальных пиков:
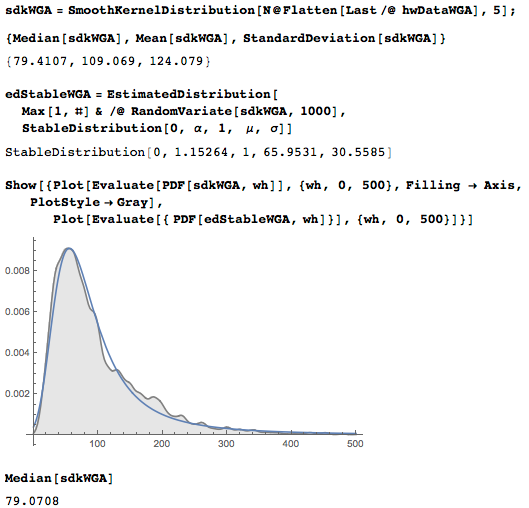
Покажем распределения возрастов картин из этого набора данных (в оригинале статьи приложена неверная картинка (дубль предыдущей), что было исправлено — прим. ред.):
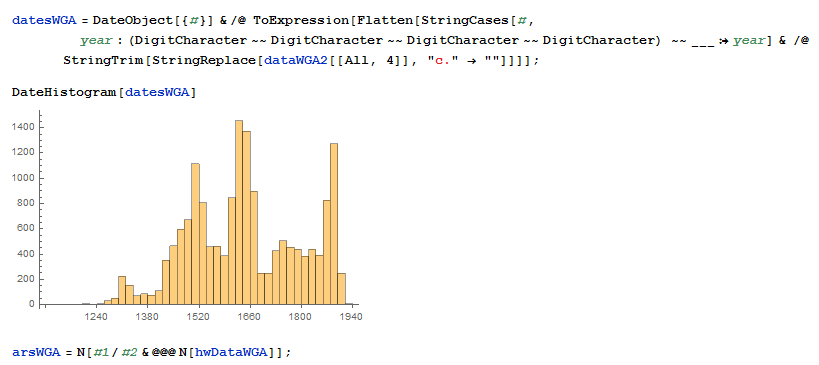
Проанализируем этот набор данных, построив все соотношения сторон вместе с их кратными числами:
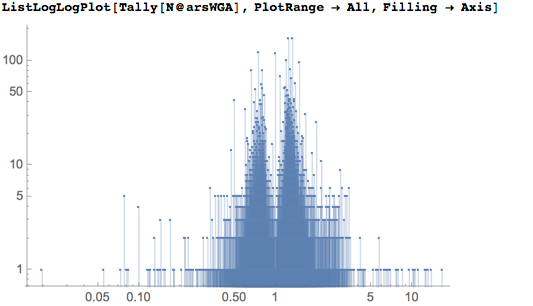
Чтобы иметь возможность представить очень близкие кратные числа соотношений сторон, выберем ширину столбца гистограммы равной 0.02:
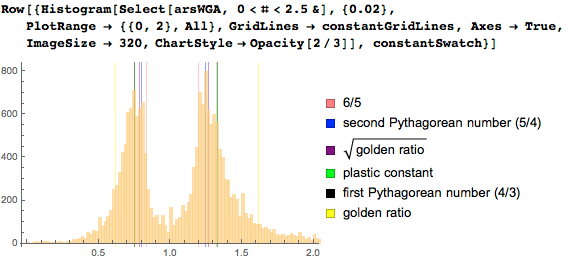
Давайте теперь представим каждое соотношение в виде некоторой дроби таким образом, чтобы ошибка составляла менее одного процента. Как будут распределены подобные аппроксимирующие дроби? Следующий график представляет распределение на логарифмической оси. Интересно отметить, что большая часть картин в соотношениях максимум(ширина/высота) / минимум(ширина/высота) и минимум(ширина/высота) / максимум(ширина/высота) часто содержат знаменатели 3, 4 и 7, а 6 и 18 практически отсутствуют:
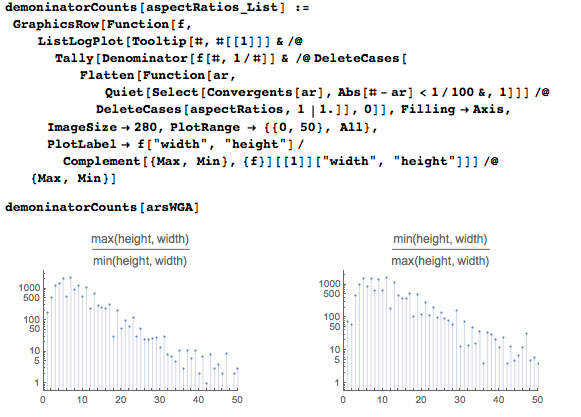
Для сравнения, вот соответствующие графики для 20 000 равномерно (в промежутке [0,2]), распределенных чисел:
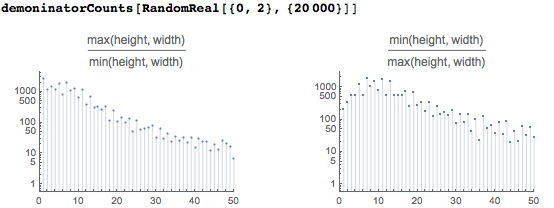
Вот функции распределения картин с выбранными соотношениями сторон:
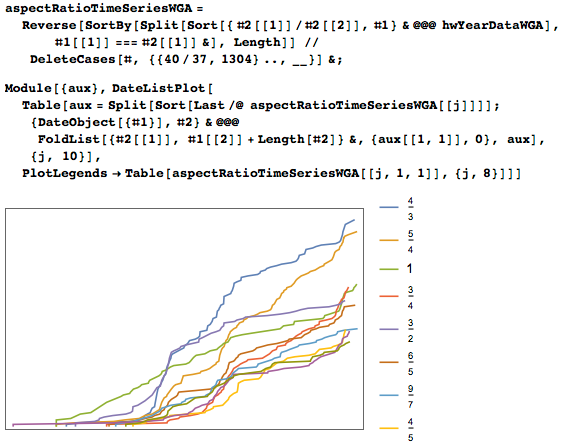
Если построим доли картин с соответствующими соотношениями сторон от общего числа картин, то мы по прежнему будем видеть увеличение картин с соотношением сторон 5/4, притом доли остальных картин существенно не меняются:
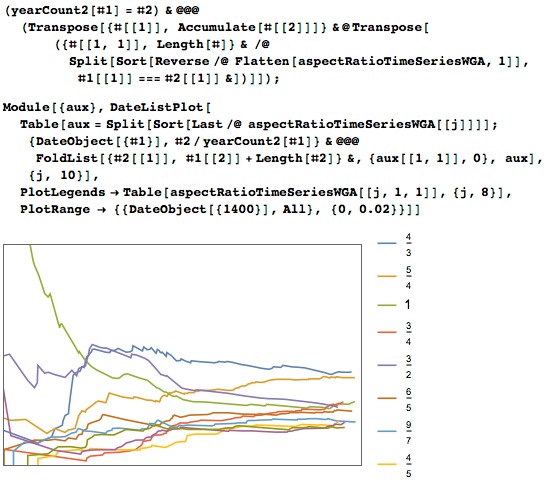
Если не брать значения размеров как точные, а предположить, что они являются точными лишь до ± 1%, то мы получим совсем другую картину. На следующем рисунке показано распределения картин с заданным значением точного значения соотношения сторон картин с принятым нами отклонением. В 16-ом веке все основные соотношения сторон были распространены примерно одинаково. Можно заметить, что соотношения 5/4, 4/3 и 9/7 стали заметно более популярными в 17-ом веке. А пропорции, близкие к золотому сечению, поубавили популярности с 13-го века. Данный график не чувствителен к процентному изменению ширины; изменения до ± 5% дадут весьма близкие результаты.
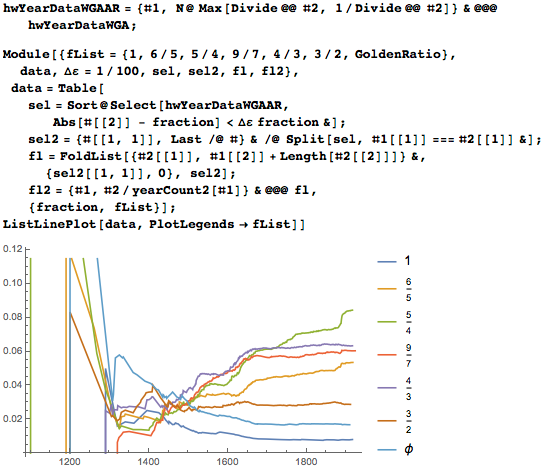
Так что можно сказать о знаменателях в наиболее распространенных соотношениях? Сформируем все дроби с максимальным знаменателем 16 и отобразим все соотношения к ближайшим из этих дробей. Из-за неравномерных промежутков между выбранными рациональными числами нам следует привести число соотношений сторон, соответствующих каждой из дробей, в соответствии с расстоянием до ближайшей меньшей и большей дроби. График дает представление о встречающихся соотношениях, что является дополнением к построенной гистограмме. В гистограмме используются столбцы равной ширины; а в следующем ниже графике используются неравные столбцы, и прилегающие минимумы и максимумы не могут перекрывать друг друга. Опять-таки, 5/4 и 4/5 — лидеры общего соревнования:
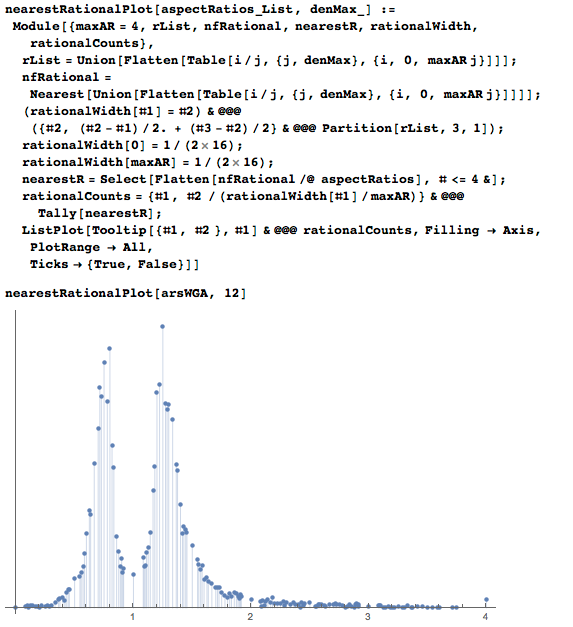
Мы снова воспользовались функцией Nearest для построения подробного распределения соотношений сторон. Следующая функция windowedMaximaPlot строит распределение либо в трёхмерном пространстве, либо как контурный график с регулируемым временным окном:
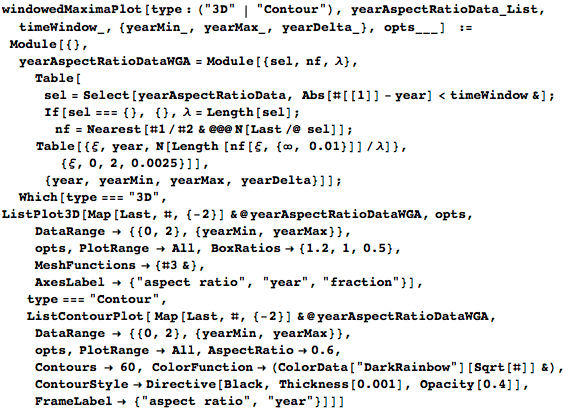
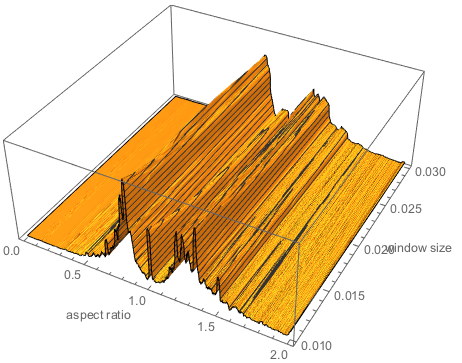
Вот трёхмерный и контурный графики:
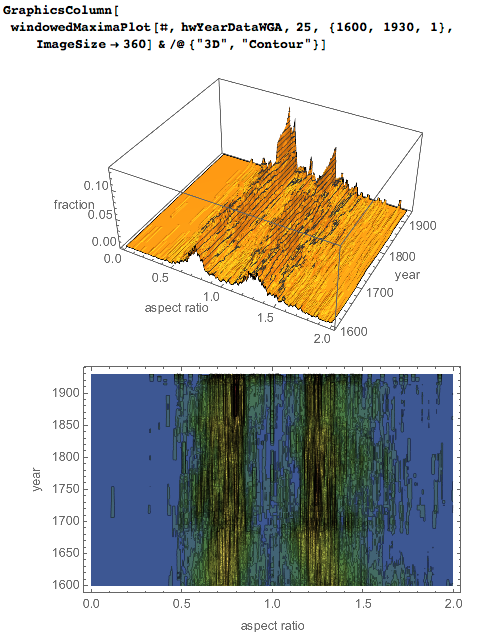
Последние два изображения указывают на несколько примечательных особенностей:
- Последние 400 лет высокие картины часто имеют соотношение сторон около 1.2.
- Наиболее распространенное соотношение сторон для широких картин поменялось в середине 18-го века, а относительно широкое распределение содержит несколько выраженных максимумов, например в 0.8.
- Квадратные картины начинают набирать популярность с начала 19-го века.
Labreuche рассуждает о процессе стандартизации полотен. Во Франции первая стандартизация произошла в семнадцатом веке, а вторая — в девятнадцатом (о недавних временах и с большим количеством математики см. работу Dinh Dang). Simon обсуждает стандартизацию холста в Великобритании.
Вот размеры для некоторых стандартизированных французских полотен девятнадцатого века. Данные в формате
{ширина, {высота портрета, высота пейзажа, высота марины (морского пейзажа)}}:
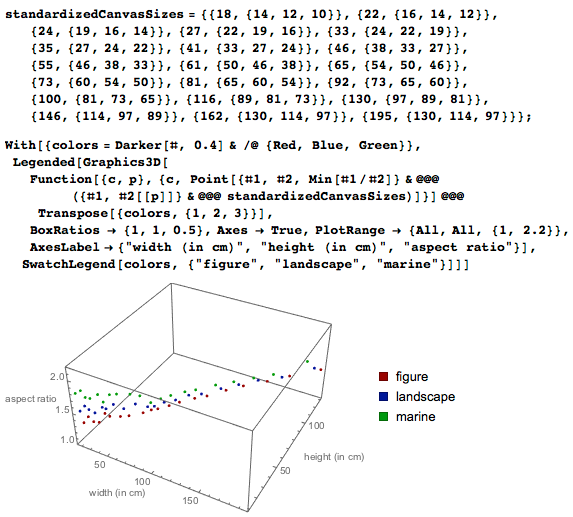
Соотношения сторон (максимум(высота/ширина, ширина/высота)) для всех полотен имеют следующее распределение:
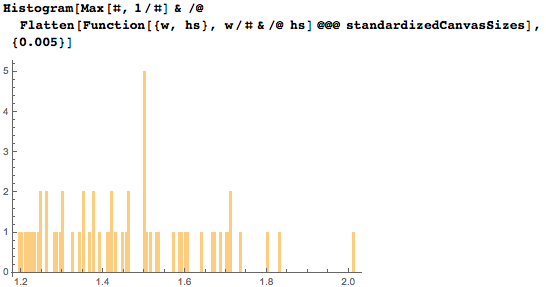
Нелегко найти большие и точные наборы данных по размерам старых картин. С другой стороны, различные веб-сайты имеют десятки тысяч изображений картин как в JPG, так и в PNG. Может, соотношения сторон стоит просто посчитать через соотношения количеств пикселей по ширине и высоте? Выше мы видели, что большинство картин измеряется с точностью до примерно одного сантиметра. Со средней высотой и шириной картин около одного метра мы получаем погрешность около 2%. Даже уменьшенные изображения размером в приблизительно 100 пикселей или в ширину/высоту в несколько сотен пикселей. Таким образом, можно было бы снова ожидать результатов, верных в точности до 1..2%. Но нет никакой гарантии, что изображения не были обрезаны, что рамка была включена в размер, имеются или нет граничные пиксели. Веб-галерея искусств имеет, в дополнение к фактическим размерах картин, их изображения. После загрузки изображений и расчета соотношений сторон попробуем сравнить их с соотношениями, рассчитанными на основе реальных высот и ширин картин. Вот итоговое распределение двух соотношений (картин и их изображений) вместе, а также модель данного распределения, представленная как CauchyDistribution[1.003, 0.019]. Среднее значение от двух пиксельных измерений — 1.036, стандартное отклонение — 0.38. Эти числа показывают, что ошибка от использования изображений для определения соотношения сторон является слишком большой для того, чтобы надлежащим образом передать мелкомасштабную структуру распределения:
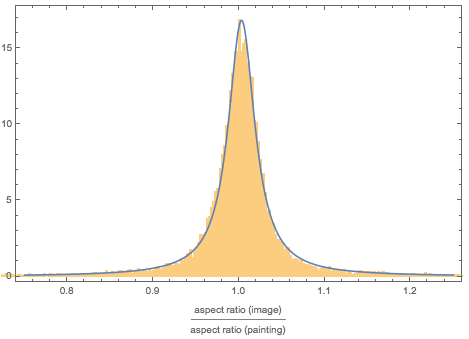
В данных dataWGA хранится информация и о художниках. Меняется ли среднее соотношений размеров в картинах в течение жизни художника? Вот распределение соотношений картин по ходу жизни художников:
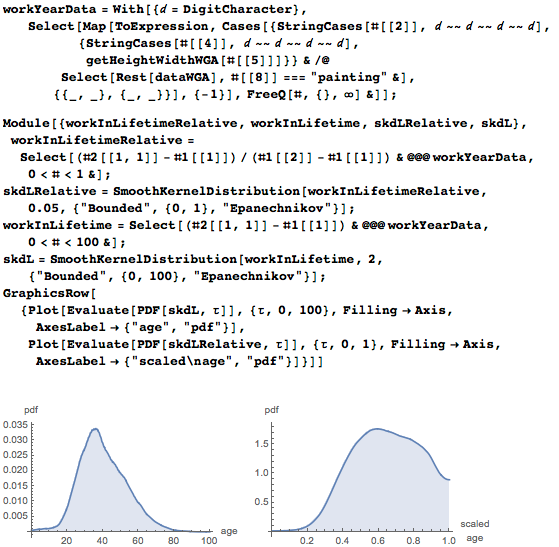
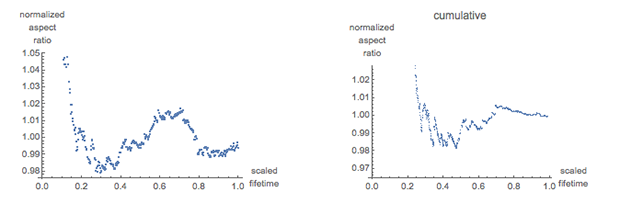
Мы можем увидеть общий шаблон изменения среднего соотношения сторон для картин художника в зависимости от его возраста. Первые картины статистически имеют более экстремальные пропорции. В конце первой трети жизни соотношение сторон минимально, а в конце второй трети соотношение сторон максимально (левый график). Совокупное среднее соотношение сторон показывает минимум на ~0.4 от продолжительности жизни живописцев (график справа). Оба графика показывают максимум(высота/ширина, ширина/высота), разделенный на среднее значений всех соотношений сторон. (Связь творчества и возраста обсуждается здесь).
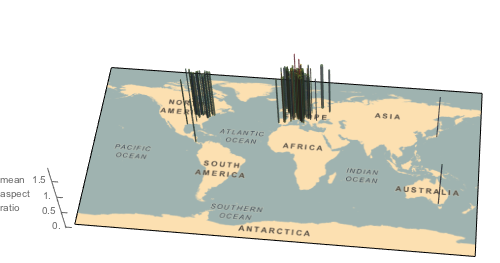
Читатель при желании может самостоятельно провести более точные замеры некоторых картин; тем временем, проведем некоторые расчёты с данными по веб-галерее изящных искусств. Давайте также рассчитаем и визуализируем распределение картин по миру. Мы берем текущие города, в которых находятся картины (которые содержат данные о ширине и высоте), как их положения, берем среднее от всех картин в этом городе и представляем максимум(высота/ширина, ширина/высота) как функцию от города. Неудивительно, что большинство крупных коллекций картин не сильно отклоняются от медианы 1.333. Чтобы найти города и работать с их локациями, будем использовать функцию Interpreter:
Примечание II: важность точности в измерениях
Давайте более пристально исследуем значения ширины и высоты. Если построить диаграмму для дробных долей сантиметров, то мы ясно видим, что подавляющее большинство картин измеряются с точностью менее 1 см. Лишь около 10% от всех картин содержат данные о размерах, указанные в миллиметрах (и некоторые из тех, что указаны с точностью до 5 миллиметров, вероятно, также округлены):
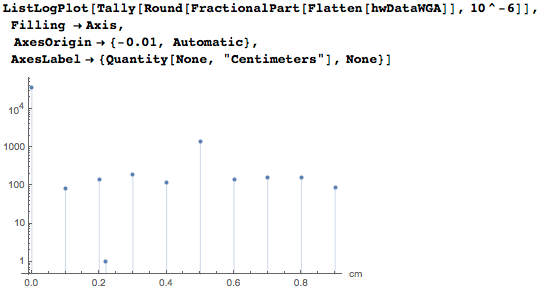
Давайте более пристально исследуем значения ширины и высоты. Поскольку большинство картин были написаны до введения сантиметра в качестве единицы измерения, популярные размеры в живописи, вероятно, не должны быть кратны сантиметру. Это означает, что измеренные значения высот и ширин не являются фактическими значениями. Утешает лишь весьма однородное распределение миллиметровых частей размеров картин, которые были измерены с точностью до миллиметра.
Во многих проанализированных наборах данных ширины и высоты картины представляются в виде целых чисел и в сантиметрах. (Явное исключение — набор данных из коллекции Тейта, в которой практически каждая картина измеряется в точности до миллиметра). Поскольку ширины и высоты большинства картин в том же порядке, что и 100 см, для точного определения соотношения сторон округление до сантиметра — операция ощутимая. Сколь много из наблюдаемых максимумов для различных дробей с малыми знаменателями являются следствием неточных значений ширин и высот?
Давайте смоделируем этот эффект. Функция aspectRatioModelValue моделирует соотношения сторон картин. Мы предполагаем устойчивое распределение ширин и то, что распределение высот есть нормальное распределение со средним значением 1.3 xwidth. И мы будем моделировать только высокие картины, ограничивая высоту так, чтобы высота была не меньше ширины:
Теперь мы «вырежем полотна» для высоких картин и посмотрим на распределение пропорций. Мы проделываем это дважды для каждого из 100 000 полотен. Верхний график содержит распределение, полученное при использовании размеров в точности до миллиметров. График ниже показывает, что в 65% всех случаев измерения точны до сантиметра, в 25% до половины сантиметра, и 10% — до миллиметра. На каждый из результатов трех вычислительных экспериментов наложим гистограмму результирующего распределения:
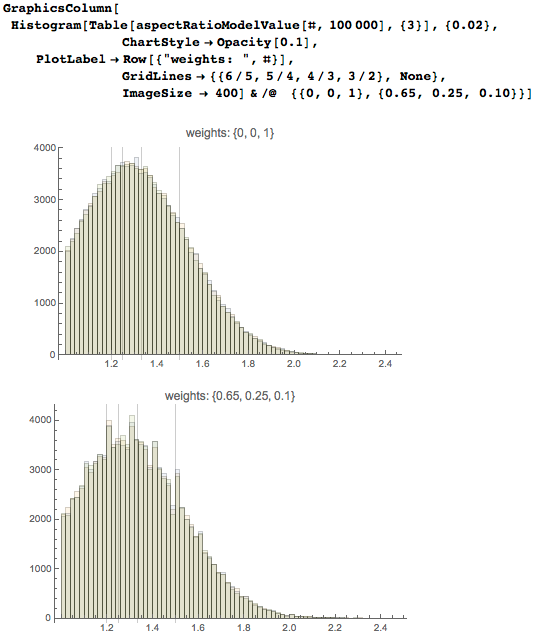
Сравнение верхнего и нижнего графиков говорит нам о том, что распределение соотношения сторон достаточно гладкое в случае, если измерения точны до миллиметра. Нижнее распределение содержит артефакты, вызванные точностью измерения до сантиметров.
Глядя на довольно гладкую гистограмму для значений миллиметровой точности и вышеприведенную гистограмму соотношений сторон коллекции Тейта можно заметить, что частые появления соотношений, представимых в виде простых дробей — реальный эффект. В то же время, как показано в вышеприведенном эксперименте с весами {0,65, 0,25, 0,10}, округление до сантиметров искусственно усиливает влияние некоторых простых дробей, таких как 6/5, 5/4, и 3/2.
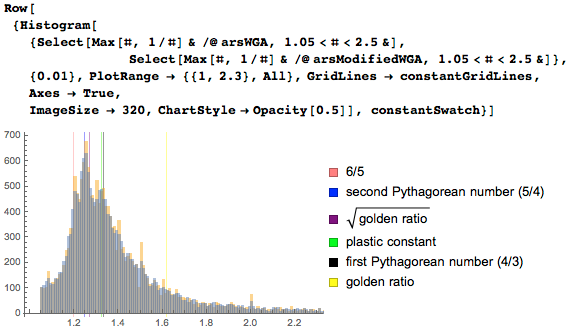
Еще более простой способ продемонстрировать влияние ошибок округления при измерениях соотношений сторон в наборе данных веб-галереи изящных искусств — самим поменять значения ширин и высот. К каждому целочисленному размеру добавим от -5 мм до 5 мм чтобы сымитировать более точное измерение. Опять-таки, в качестве соотношения сторон будем использовать отношение большей стороны к меньшей:
Наложим теперь первоначальное распределение на изменённое — то, где мы меняли значения ширин и высот. Мы видим, что максимумы на некоторых рациональных соотношениях сильно подавляются, однако глобальный максимум около 5/4 не меняет своего положения, второй максимум — 4/3 — также стабилен, равно как и малый первый максимум — 6/5. В то же время пики на 3/2 и 2 сильно теряют в высоте:
Сделаем всё в обратной последовательности с набором данных коллекции Тейта: округлим все ширины и высоты до сантиметра. Опять же, построим изначальное распределение соотношений сторон вместе с измененным:
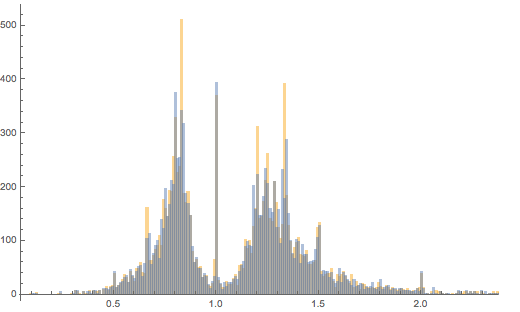
В то время как высоты локальных пиков изменились, самые крупные пики по-прежнему присутствуют, притом весьма выражено.
WikiArt: еще один крупный веб-ресурс
Давайте рассмотрим еще один крупный веб-ресурс — WikiArt. Для вычислительных задач этот сайт структурирован очень удобно. Мы имеем список из 900+ художников с гиперссылками на страницы с их произведениями. Каждая картина имеет свою страницу, которая содержит удобно структурированную информацию. Вот, к примеру, информация о картине Мона Лиза:
Отметим, что приведенные выше данные содержат информацию о стиле и жанре. Это предполагает использование набора данных WikiArt для поиска возможных зависимостей форматов от жанра (стили мы уже рассматривали выше).
В наборе данных имеется около 7000 картин с информацией об их размерах. Для краткости, все данные были закодированы в виде одного черно-белого изображения:
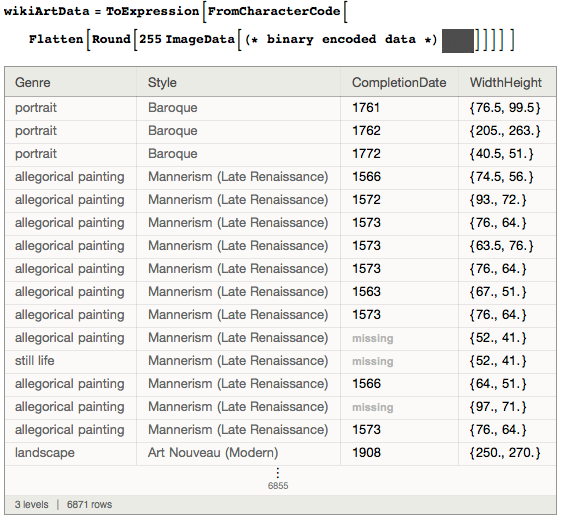
Картины с информацией о размерах имеют следующее распределение по их возрасту. Можно заметить преобладающее количество картин из восемнадцатого и девятнадцатого веков:
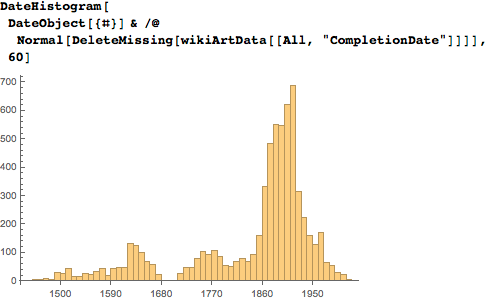
На основании полученных ранее результатов можно ожидать, что этот набор данных, в котором преобладают картины последних полутора веков, будет иметь явные пики на соотношениях сторон, которые соответствуют некоторым дробям. Представленное ниже распределение с вертикальными линиями на 6/5, 5/4, 4/3 и 3/2 подтверждает эту гипотезу:
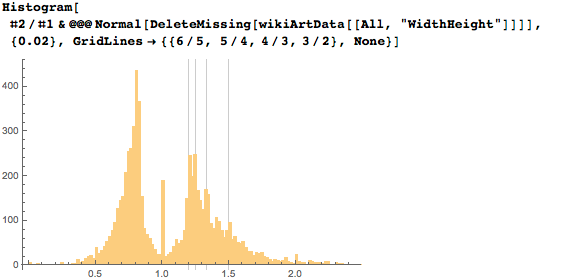
Жанр, очевидно, тесно связан с форматом картины — будет ли она широкая, квадратная или высокая. Вот соотношения долей широких, квадратных и высоких картин для различных жанров:
Давайте теперь рассмотрим распределение соотношений сторон как функцию от жанра:
С помощью функции TimelinePlot, изобразим диапазоны второго и третьего квартилей соотношений:
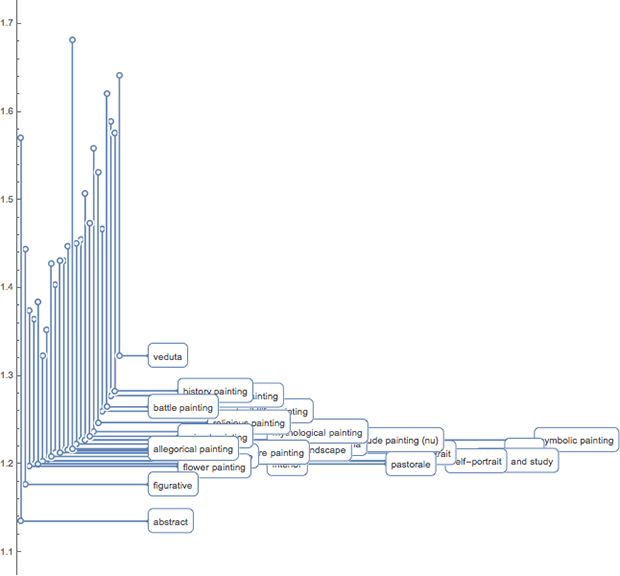
Высокие картины в пейзажах встречаются гораздо реже, чем широкие. Но даже если мы под соотношением сторон будем подразумевать отношение длинной стороны к короткой, то мы по-прежнему будем видеть четкую зависимость пропорций от жанра.
Жанр часто также влияет и на сам размер картины. Вот второй и третий квартили в соотношениях сторон и площадях для различных жанров (в приложенном документе Mathematica эта картинка интерактивна: наведите курсор на непрозрачный прямоугольник, чтобы увидеть жанр):
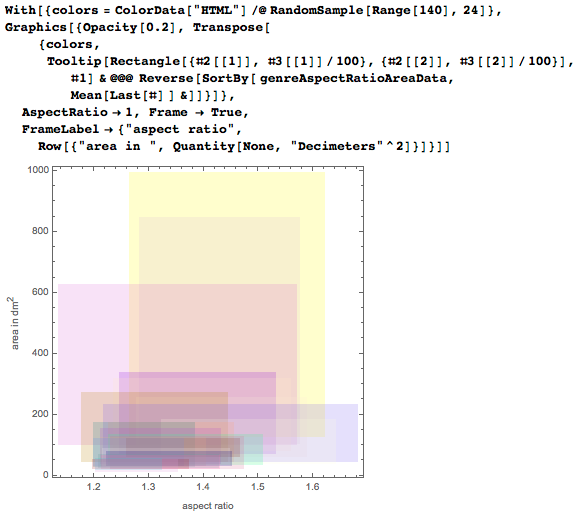
Если мы разделим каждый жанр по стилям, то получим более мелкозернистую структуру распределения соотношений сторон. Выберем 50 самых популярных жанров и стилей, каждый из которых должен быть представлен по крайней мере пятьюдесятью картинами:
Неоклассические картины в стиле ню выделяются наибольшим средним соотношением сторон (около 1.86):
А вот более подробная диаграмма, показывающая средние соотношения сторон для различных стилей и жанров, которые содержат по крайней мере пять картин. (Наведите курсор на вертикальную колонну, чтобы увидеть жанр и пропорции.)
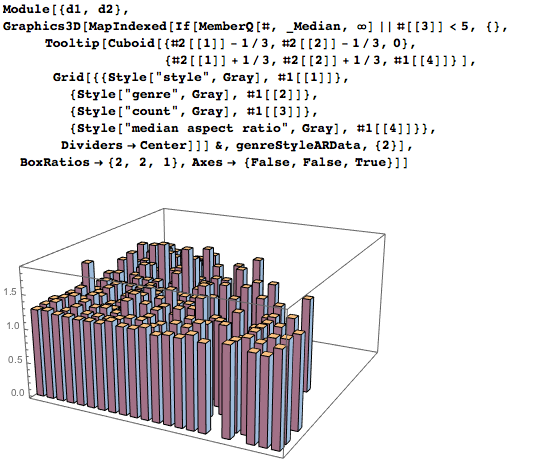
Коллекция Французского государственного музея
Как мы увидели выше, коллекции живописи в несколько тысяч картин выдают несколько максимумов в распределении соотношений сторон в диапазоне 1.24 — 1.33. Давайте рассмотрим теперь второй по счету большой набор данных.
Каталог французских национальных музеев Joconde содержит описания более полумиллиона предметов искусства. Поиск по картинам дает ~67000 результатов. Не все из них те картины, что вешают на стену; коллекция также включает в себя картины на фарфоровых фигурках и других поверхностях. Итого ~31000 картин с явно заданными размерами. Так как информация о картинах исходит от нескольких музеев, размеры могут быть представлены в различных форматах. Для извлечения размеров потребуется некоторое время.
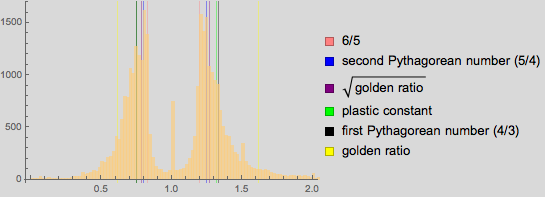
Интересно, что тут мы получаем новый максимум, равный ~1.23.
Отображение распределения широких изображений на оное для высоких изображений с заменой высоты на ширину показывает, что два максимума совпадают очень хорошо. Таким образом, соотношение 5/4 (или 4/5) — наиболее популярное:
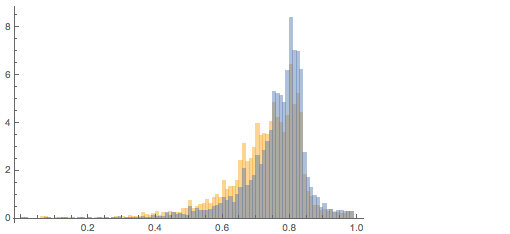
В коллекции высоких картин на ~11% больше, чем широких.
Картины в итальянских церквях: высота есть всё
Очень большую базу данных по картинам итальянских католических церквей можно найти здесь. Поиск картин, написанных маслом, дает 130 000 результатов, из которых 124 000 содержат данные по ширине и высоте.
Коллекция содержит много относительно новых картин (шестнадцатого века ≈4%, семнадцатого века ≈23%, восемнадцатого века ≈36%, девятнадцатого века ≈24%, двадцатого века ≈13%).
Вот какое распределение получается. Покажем распределение вместе с линиями на 1, 6/5, 5/4, 4/3, 7/5, 3/2, 5/3 и 2. Эти линии на удивление хорошо согласуются с положениями максимумов:
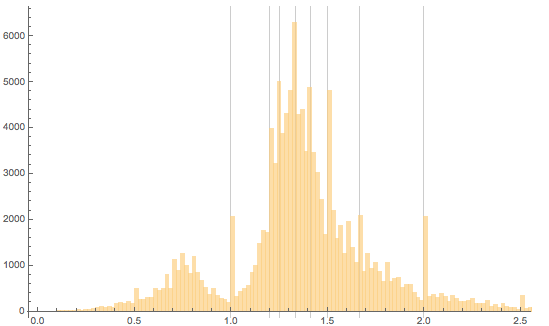
График явно указывает на существенное преобладание высоких картин над широкими. И все максимумы приходятся на дроби с малыми знаменателями. И это при том, что лишь около 8% из общего числа картин измерены с погрешностью менее половины сантиметра.
Смитсоновская коллекция
Смитсоновский музей американского искусства имеет сайт, с помощью которого можно исследовать большое количество картин. Около 286000 картин содержат информацию о размерах. Вот полученное распределение пропорций:
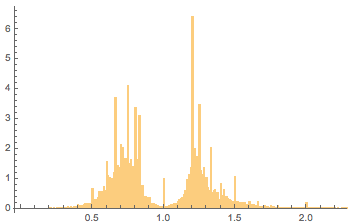
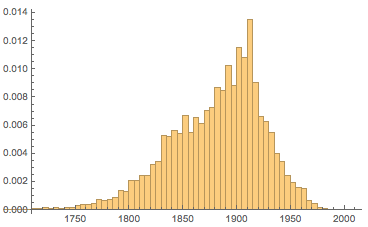
Как было отмечено, выраженные пики на рациональных дробях чаще наблюдаются для картин последних 200 лет. Вот график распределения возрастов картин из этой коллекции, который это подтверждает:
Большая коллекция картин в Великобритании
Третий большой набор данных почерпнем с британского сайта Your Paintings, который представляет 200000+ картин, 56000 из которых имеют данные о ширине и высоте.
В отличие от предыдущих наборов данных, многие из картин этой коллекции моложе 150 лет. Получается, преобладание новых картин должно поменять распределение соотношений сторон?
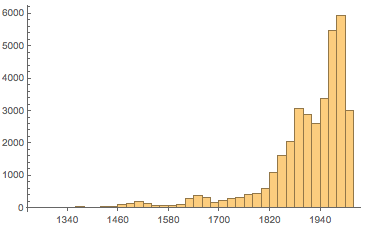
Мы снова наблюдаем ярко выраженный максимум. Пять наиболее выраженных максимумов для высоких картин приходятся на дроби с малыми знаменателями. Изобразим в качестве вертикальных линий числа 6/5, 5/4, 9/7, 4/3, 3/2 и их обратные значения. Для широких картин мы видим те же (то есть инвертированные) позиции максимумов, что и для высоких картин:
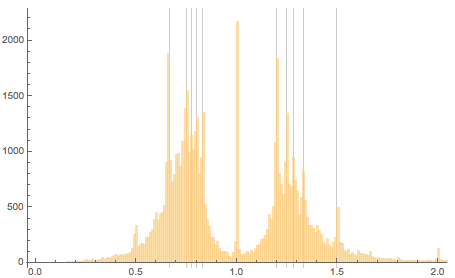
Отличная новость — 52% всех размеров задаются точнее, чем в сантиметрах. Это означает, что видимые максимумы — не просто дефекты округления, а картины и правда чаще имеют соотношение сторон, выражаемое в виде дроби с малым знаменателем.
А вот график числа картин с более высоким разрешением и с максимальной дистанцией от заданного соотношения сторон, равной 0.01:
Нынешний рынок изящных искусств: рациональней чем когда-либо
Последний раздел с британскими картинами за последние 150 лет показывает четкую тенденцию к использованию в качестве соотношения сторон рациональных чисел с малыми знаменателями. Возникает вопрос: какое соотношение наиболее популярно в наши дни?
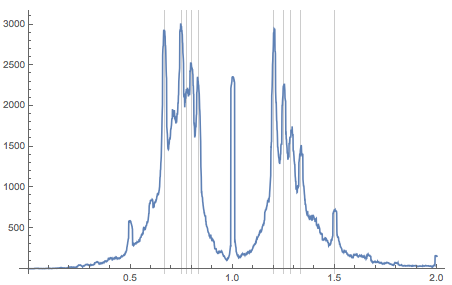
Нет такого музея, который имеет тысячи картин последних лет (по крайней мере, я не смог такого найти). Итак, давайте обратим внимание на дилеров современных картин (нескольких последних десятилетий). После некоторых поисков я вышел на Saatchi Art. Поиск по картинам, написанных маслом, выдал 96000 картин. Итак, какие у них соотношения? Вот график с распределением их пропорций. Вертикальные линии проведены на значениях 1, 6/5, 5/4, 4/3, 3/2, 2, и соответствующих им обратных значениях. Обратите внимание, что на этот раз мы используем логарифмическую вертикальную шкалу:
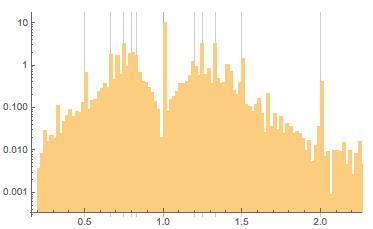
В самом деле, все тенденции, которые были заметны в наборе данных Your Paintings, стали еще более выраженными:
- еще большая доля квадратных картин,
- выраженные максимумы на соотношениях сторон, которые есть рациональные числа с малыми знаменателями — как для широких, так и для высоких картин,
- почти равное количество широких и высоких картин.
Максимумы в определенных соотношениях отражаются на распределении площадей картин — наблюдается несколько десятков выраженных значений:
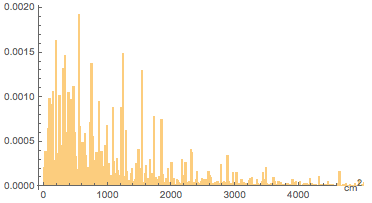
Можно предположить, что они вызваны размерами промышленно изготовленных полотен. Чтобы проверить это предположение, проанализируем имеющиеся в продаже картины магазина Dick Blick:
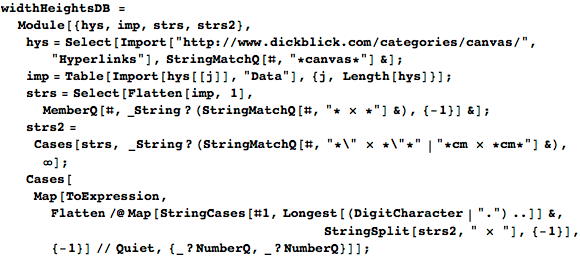
Построенное распределение площадей для ~1600 полученных картин имеет те же ключевые черты, что и указанное выше распределение:
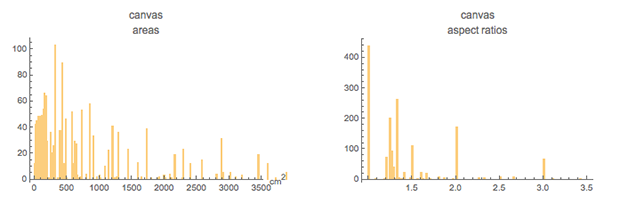
На построенном с помощью aspectRatioCDFPlot представленном выше распределении можно заметить наиболее распространенные пропорции, которые проявляются в виде вертикальных сегментов:
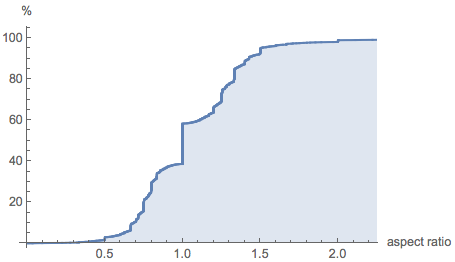
И пусть невозможно купить картины в музее, их можно купить в Saatchi. Таким образом, для этого набора данных мы можем рассмотреть вопрос связи между ценой и соотношением сторон. (Для различных статистических данных по ценам и качественным свойства картин см. Reneboog и Van Houtte, Higgs и Forster и Bayer и Page.)
Данные не указывают на явную зависимость цены картины от её соотношения сторон:
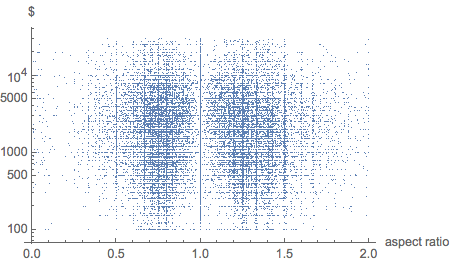
В то же время наблюдается слабая корреляция между ценой и площадью по закону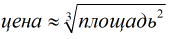 
. (Для детального изучения отношения площадей к ценам корейских картин см. Nahm).
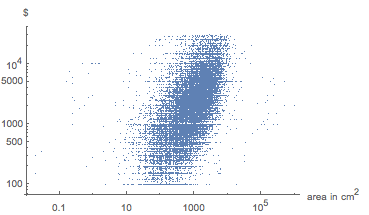
Проданные картины: большинство написаны недавно, а у распределения длинный хвост
Ранее мы рассмотрели соотношения сторон картин из различных музейных коллекций. В последнем разделе мы рассмотрели соотношения сторон картин, представленных к продаже. А что можно сказать о пропорциях недавно проданных картин? Сайт Artnet — отличных источник информации о проданных на аукционах картинах. Он содержит около 590000 картин с информацией о размерах.
В то время как картины, проданные с аукциона, могут быть и средневековыми, всё-таки большинство относятся к современным. Вот кумулятивное распределение картин за последнее тысячелетие. Обратите внимание на то, что вертикальная ось — логарифмическая. Мы видим распределение по принципу Парето — 90% всех проданных на аукционе картин сделаны после 1855:
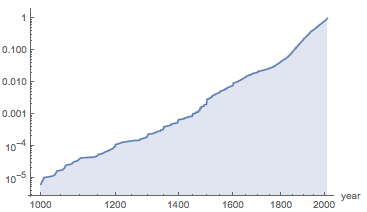
Основываясь на нашем предыдущем анализе, можно ожидать, что набор данных со столь большим количеством относительно новых картин будет иметь сильные и выраженные пики на рациональных числах с малыми знаменателями, плюс ожидается много квадратных картин. И это действительно так, и это подтверждает представленный ниже график. Построим распределение вместе с вертикальными прямыми на 5/6, 4/5, 3/4, 2/3, 5/7, 7/10 и обратных им:
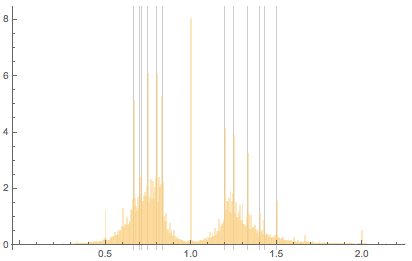
Даже на логарифмической шкале пики на этих значениях все еще ясно видны:
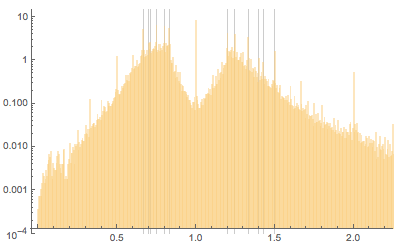
Относительное число картин с соотношением сторон, близким к некоторым простым дробям, увеличивается с течением времени. Для соотношений сторон из интервала [1.1, 1.4] построим абсолютное значение разности между функцией распределения вероятности и её сглаженной версией (с радиусом сглаживания в 0,01). Хорошо видны относительные увеличения максимумов на 6/5, 5/4, 4/3:
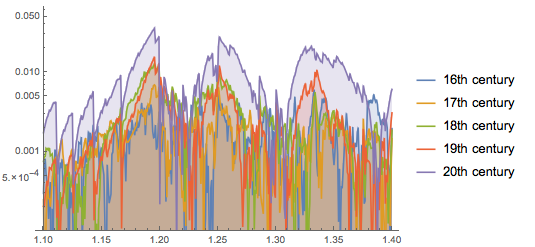
Картины из этого набора данных по большей части написаны маслом. Однако интересно было бы сравнить распределения соотношений сторон картин, написанных маслом, акварелью, акрилом. Акрил используется лишь с семидесятых, поэтому пики на дробях с малыми знаменателями становятся еще более выраженными. Распределение соотношений сторон для туши имеет совершенно другую форму — возможно, из-за форматов бумаги:
Большое количество картин сильно увеличивает вероятность нахождения картин с экстремальными пропорциями. Имеются даже соотношения, меньшие 1/10 и большие 10. Примеры очень широких картин: Hussainbad Imambara Complex, Makimono scroll of river scenes, Sennenstreifen. Примеры очень высоких картин: La salive de dieu, Pilaster, Exotic rain.
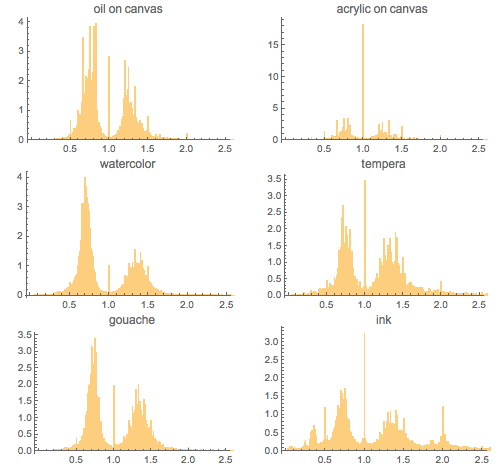
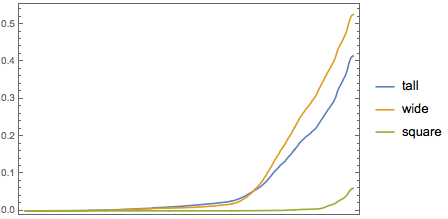
Если мы посмотрим на кумулятивное распределение всех картин, которые делятся на широкие, высокие и квадратные, то мы видим, что с 1825 года широкие картины становятся все более популярными. Можно также заметить увеличение количества квадратных картин после 1950:
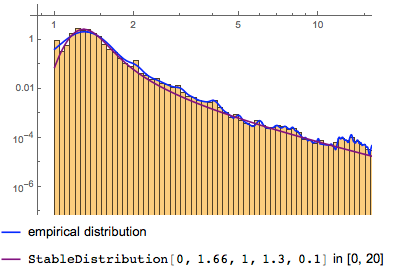
Большое количество картин в этом каталоге вместе с возникновением выделяющихся пропорций в этом наборе данных позволяют предложить, что мы должны применять ту же модель распределения для всех соотношений максимум(высота/ширина, ширина/высота). Используя данные (которых значительно меньше) из встроенной бызы данных «Artwork» (изящных искусств), мы предположили, что распределение пропорций хорошо аппроксимируется устойчивым распределением. Попробуем найти модель для нашего распределения. Синяя кривая, представляющая распределение, была получена сглаживанием с шириной 0.1:
Сайт известного аукционного дома Sotheby имеет базу данных с возможностью поиска из более чем 100000 картин, которые продавались в последние 15 лет. Проверим теперь, имеется ли зависимость между ценой и соотношением сторон. Вот финальные цены проданных картин в зависимости от соотношений сторон:
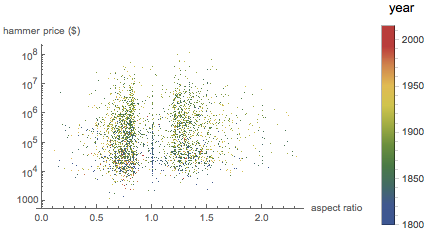
Аналогичным образом, прямой связи между ценой с молотка и площадь картины не наблюдается:
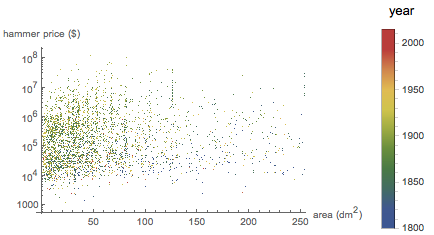
Распределение аукционных цен интересно само по себе, однако мы не будем на это отвлекаться и продолжим фокусироваться на соотношениях сторон:
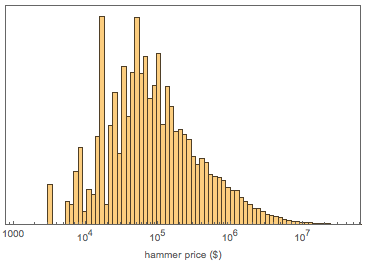
Восток: все показатели отличаются
Практически все картины, которые мы рассматривали, были написаны западными художниками. Но что можно сказать о Востоке? Оказалось, что гораздо труднее найти базу данных восточных картин. Самая обширная из тех, что мне удалось найти — каталог китайской живописи в университете Токио.
Веб-страницы весьма удобно структурированы и мы можем легко их импортировать. Вот пример:
Типичный ввод данных с размерами:
В базе данных содержится ~10500 картин с размерами. Вот распределение соотношений сторон:
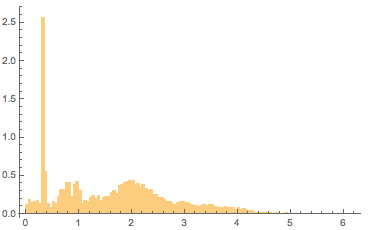
Распределение заметно отличается от оного для западных картин. Наиболее выраженные максимумы в положениях 1/3 и 2. Для более детального изучения китайской живописи см. Zheng, Weidong и Xuchen. Тут можно найти другую, меньшую онлайн коллекцию китайской живописи.
Пропорции пакетов, автомобилей, этикеток, логотипов, эмблем, бумаги, банкнот, почтовых марок и фильмов
Художники предпочитают определенные соотношения сторон для картин исходя из эстетических соображений; возможно, схожие шаблоны проявляются во многих объектах современного мира.
Продукты из супермаркета
Давайте рассмотрим различные продукты из супермаркета. В конце концов, они своим видом напрямую обращаются к потенциальным клиентам. Сайт ItemMaster имеет список десятков тысяч разных продуктов (там требуется регистрация).
Вот, снова гистограмма соотношений высота/ширина. Многие упаковки продуктов — квадратные (и этот тренд значительно выраженнее, чем для картин). И наиболее распространенное соотношение высота/ширина очень близко к 3/2:
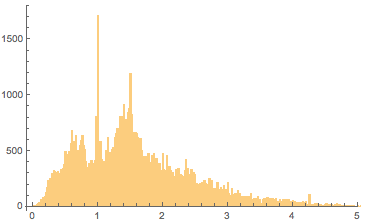
(См. Raghubir и Greenleaf, Salahshoor и Mojarrad, Ordabayeva и Chandon и Кох для более подробного знакомства с оптимальными формами упаковки с эстетической точки зрения, а не с производственной).
Винные этикетки
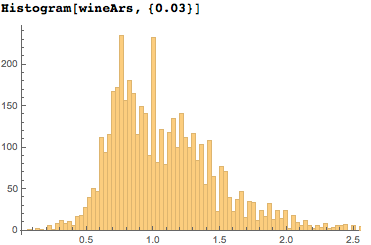
После быстрого взгляда на размеры упаковок, думаю, логичным будет исследовать этикетки на продуктах. Трудно найти их явно заданные размеры, однако с их изображениями проблем не возникает. Ранее, при анализе данных веб-галереи изящных искусств, мы выяснили, что анализ размеров изображений, а не оригиналов, даёт определенную погрешность. Это означает, что мы не сможем построить точный график распределения пропорций этикеток, однако анализ их изображений позволит получить общее представление о распределении. Рассмотрим этикетки красных вин и немецких сортов пива. Сайт wine.com содержит около 5000 этикеток красного вина:
Интересно, что распределение пропорций винных этикеток не так уж и отличается от распределения картин. У нас есть широкие, высокие и квадратные этикетки:
Этикетки немецких сортов пива
Сайт Catawiki содержит около 2700 этикеток немецких сортов пива. Несколько минут, и мы получим ширины и высоты всех пивных этикеток:
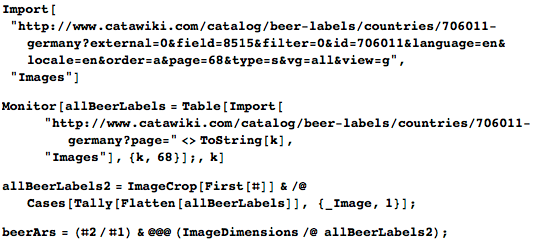
Распределение пропорций этикеток пива заметно отличается от винных. Большинство пивных этикеток почти-что квадратные:
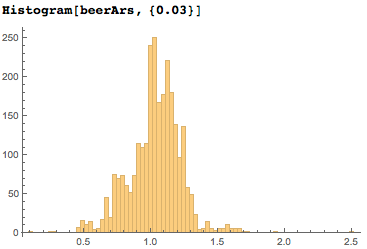
Логотипы продуктов питания
Обобщим и включим последние два набора данных в продукты питания. Сайт brandsoftheworld.com содержит ~9000 логотипов продуктов питания и напитков. Вот распределение их соотношений сторон. Мы ясно видим, что большинство логотипов либо широкие, либо квадратные. Есть и высокие логотипы, но их намного меньше, чем широких:
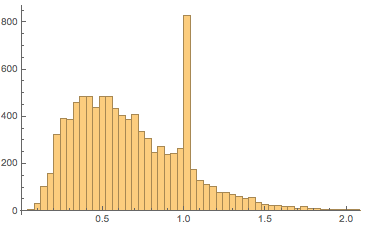
Банкноты
Что можно сказать о том, что мы используем, чтобы заплатить за продукты — о банкнотах? Банкноты доступны через фреймворк Entity, и мы можем быстро проанализировать соотношения сторон для ~800 банкнот, которые в настоящее время используются в разных странах:
Практически все современные банкноты широкие, потому мы видим лишь соотношения, меньшие единицы. И большинство банкнот ровно в два раза больше в ширину, чем в высоту:
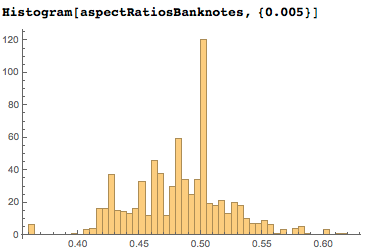
Размеры автомобилей
Если есть достаточно купюр, то можно купить хороший автомобиль. Итак, каковы распределения соотношений сторон автомобилей? Включив около 3600 моделей автомобилей 2015 года, получим следующие распределения:
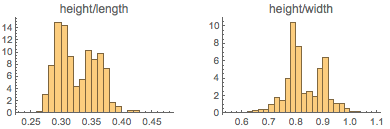
Вот некоторые из автомобилей с малыми и большими пропорциями высота/длина:
В распределении высот автомобилей отчётливо видна бимодальность. В то время как распределения длин и ширин машин унимодальны, высота показывает два четких максимума. Автомобили с высотой более 65 дюймов — в основном внедорожники и кроссоверы. Кроме того, очень маленькие автомобили средней высоты, но с длиной ниже среднего, образуют пик в соотношении высота/ширина вблизи 1/3:
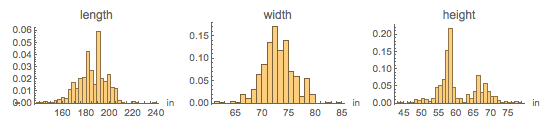
Бумажные листы
Банкноты делаются из подобных бумаге материалов. Каковы же соотношения наиболее популярных форматов бумаги? Страница в Википедии о размерах бумаги содержит 13 таблиц популярных форматов бумаги. Не представляет труда импортировать таблицы и извлечь столбцы таблиц, содержащие данные по ширине и высоте (в миллиметрах):
Также получаем распределение пропорций. Неудивительно, что мы видим четкую кластеризацию пропорций рядом с 1.41 — примерным значением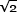 
— соотношением, на котором базируется большинство форматов, стандартизированных ISO. А наиболее распространенное соотношение — 4/3:
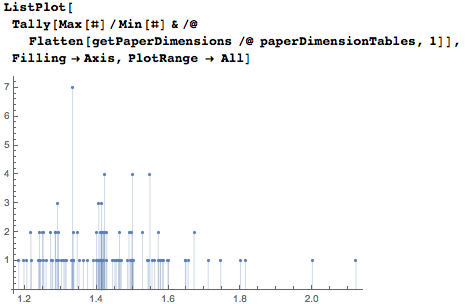
Марки
Что это может быть — похожее на картины, прямоугольное и самых разных видов? Конечно, это марки — эдакие мини-картины. Сайт Colnect содержит данные о 500000+ марок. Если мы ограничимся французскими марками, выпускаемыми с 1849 по 2015, то мы получим ~6000 марок для анализа. Чтение данных занимает несколько минут:
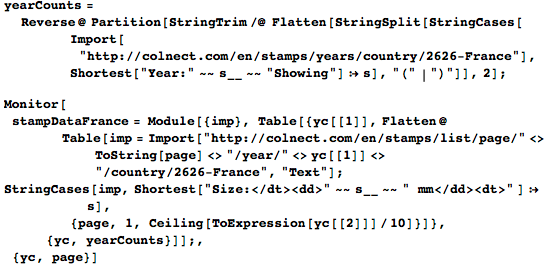
Вот кумулятивное распределение пропорций марок:
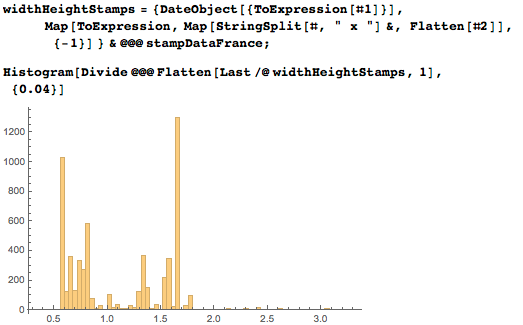
Наконец, мы нашли что-то, для чего распределение соотношений сторон имеет максимум, близкий к золотому сечению. Вот самые популярные соотношения сторон:
Изменение среднего соотношения сторон (макс(ширина, высота)/мин(ширина, высота)) указывает на изменение стиля французских марок с течением времени. Рассмотрим также, как площадь марок менялась с течением времени (в см²). Совершенно очевидно, что марки с годами становились всё больше:
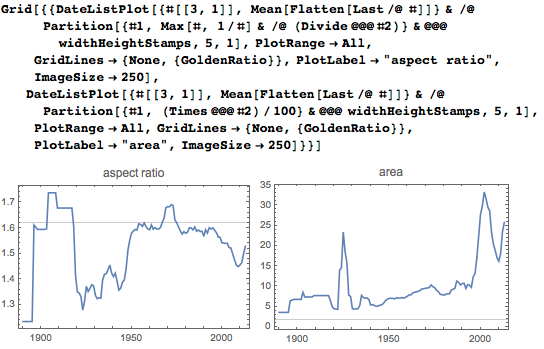
Эмблемы команд NCAA (Национальной ассоциации студенческого спорта)
Многие любят смотреть спортивные состязания, особенно командных видов спорта. Эмблемы команд часто находятся на самом виду. Давайте рассмотрим спортивные команды из двух областей: из NCAA и немецких футбольных клубов. Используемые ранее эмблемы можно найти здесь, а текущие — здесь.
Вот распределение соотношений (высота/ширина) эмблем команд NCAA. Интересно — наблюдается максимум на ~0,8, как и на некоторых распределениях для картин:
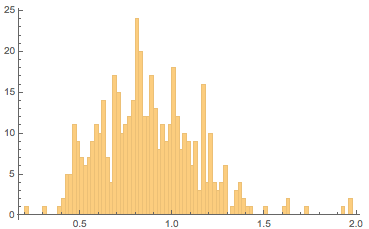
Эмблемы немецких футбольных клубов
Вот распределение соотношений (высота/ширина) для 1348 эмблем немецких футбольных клубов. Мы видим ярко выраженный максимум для квадратных эмблем и локальный максимум для высоких эмблем с соотношением сторон 1.15:
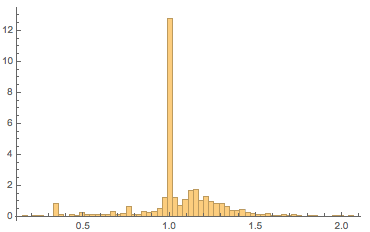
Форматы фильмов
Закончим наш предпоследний раздел для соотношений сторон прямоугольных объектов, рассмотрев эволюцию форматов фильмов. Сайт filmportal содержит список из 85000 немецких фильмов, сделанных за последние 100 лет. 27000 из них имеют данные о соотношении сторон и длительности — около трёх лет непрерывного просмотра кино. На рисунке ниже показано кумулятивное распределение пропорций в кино за длительное время. Получается, что около двух третей из всех когда-либо выпущенных фильмов имеют соотношение сторон ~4/3. И только в 60-х появилась тенденция снимать широкоформатное кино:
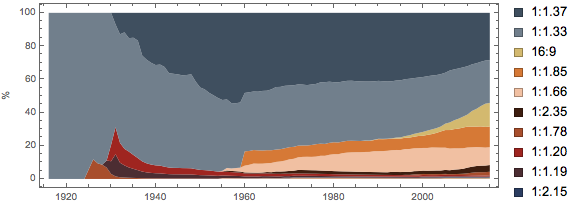
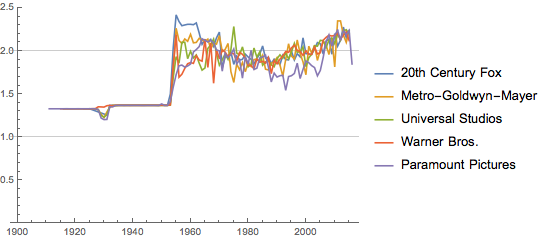
Исследуем эволюцию пропорций фильмов крупных студий США (Warner Bros., Paramount Pictures, Twentieth Century Fox, Universal Pictures и Metro-Goldwyn-Mayer) за последние 100 лет. Соотношение сторон около 4/3 стало преобладать после 1955, а сегодня среднее соотношение — около 2.18:
Заключение: так какое соотношение самое «лучшее»?
Подводя итог: мы проанализировали соотношения сторон для большого количества коллекций живописи — 1000000+ картин по количеству и за тысячелетие по времени.
Используя комбинацию встроенных и источников данных из интернета, мы получили следующие качественные выводы:
- Количество широких и высоких картин приблизительно равно для разных коллекций.
- С ХIХ века широкие картины популярнее высоких.
- Распределение широких картин может быть точно определено как обратное распределение высоких картин.
- Распределения соотношений сторон во многих коллекциях содержат (как для высоких, так и для широких картин) по крайней мере два четко различимых глобальных максимума: около 1.3 и около 1.27 (и их обратные величины для широких картин).
- Начиная с восемнадцатого века соотношения сторон, выражаемые через дроби с малыми знаменателями, становятся всё более популярными, и эта тенденция продолжается до сих пор; сроки совпадают с французской стандартизацией размеров холста.
- Распределения соотношений сторон картин 19 и 20 веков содержат выраженные максимумы на значениях 6/5, 5/4, 9/7, 4/3 и 3/2.
- В целом, распределение соотношений сторон больших коллекций картин хорошо описывается альфа-устойчивым распределением Леви, а это означает, что распределение имеет тяжелые хвосты.
- Золотое сечение не является соотношением, сколь нибудь популярным для картин (золотое сечение в архитектуре — см. Shekhawat, Huylebrouck и Labarque, Birkett и Jurgenson и Foutakis).
- Распределение пропорций картин является уникальным и весьма отличается от распределений прямоугольных объектов с современном мире (например, этикеток, марок, логотипов и т.д.).
Причины перехода к соотношениям в виде дробей с малыми знаменателями в семнадцатом веке — открытый вопрос. Был ли переход вызван эстетическими причинами, или обусловлен особенностями промышленного производства и стандартизацией? Мы оставим этот вопрос историкам искусства.
Для более четкого ответа на вопрос о том, соответствуют ли максимумы некоторым известным константам (квадратный корень из золотого сечения, пластическая константа, 4/3 или 5/4), необходимы более точные данные по размерам картин восемнадцатого века. Многие каталоги дают размеры без указания точности измерения и входит ли рама в указанные размеры. Точность измерений чаще всего равна сантиметру. При типичных размерах картин около ста сантиметров округление до сантиметра вносит определенное количество искажений в распределение. С другой стороны, использование изображений для анализа соотношения сторон не представляется возможным, так как ошибки, вызванные обрезанием и перспективными искажениями слишком велики. Мы намеренно не объединяли данные из разных коллекций. В дополнение к вопросу определения дубликатов, следовало бы тщательно изучить вопрос о том, указаны ли размеры с рамкой или нет, а также более подробно исследовать вопрос о точности измерений указанных размеров. Подобную экспертизу искусствоведу следует проводить весьма тщательным образом.
Одна большая коллекция, которую мы не включили в исследование, может быть полезна в определении точных значений максимумов распределения соотношений сторон для 178000 старинных картин онлайн-каталога 645 музеев из Германии, Австрии и Швейцарии, которые опубликовал в интернете De Gruyter На момент написания этой статьи мне не удалось получить разрешение на доступ к данным из этого каталога. (Существуют и различные малые базы данных картин, в том числе утраченные, которые могут быть проанализированы, но они, вероятно, дадут результаты, аналогичные полученным нами).
Интересно, что последние исследования показывают, что не только люди, но и другие млекопитающие, вероятно, предпочитают пропорции около 1.2 (см. недавнее исследование Винне и др.).
На изображениях картин можно проводить самые разнообразные количественные исследования — к примеру, анализ спектрального распределения мощности пространственных частот, которые есть суть компоненты Фурье цветов и яркостей, анализ освещенности и направлений, структуры и композиции (здесь, здесь, и здесь), психологических основ цветовых структур, и автоматической классификации. Если позволит время, мы будем проводить подобные исследования и в будущем. Весьма занятное исследование большого количества аспектов 2229 картин в MoMA было проведено Roder.
И, конечно, можно проанализировать схожим образом самые разные рукотворные объекты, узнать, насколько часто в разных областях появляется золотое сечение — в автомобилях, например. Соотношения сторон можно исследовать в современном расширении понятия картин — в граффити. Можно анализировать и само содержание картины, чтобы посмотреть на частоту появления золотого сечения (см. здесь, и здесь). Оставим это читателям, заинтересовавшихся в развитии этого направления.
Автор: Wolfram Research
