Использование классических нейронных сетей для распознавания изображений затруднено, как правило, большой размерностью вектора входных значений нейронной сети, большим количеством нейронов в промежуточных слоях и, как следствие, большими затратами вычислительных ресурсов на обучение и вычисление сети. Сверточным нейронным сетям в меньшей степени присущи описанные выше недостатки.
Свёрточная нейронная сеть (англ. convolutional neural network, CNN) — специальная архитектура искусственных нейронных сетей, предложенная Яном Лекуном и нацеленная на эффективное распознавание изображений, входит в состав технологий глубокого обучения (англ. deep leaning). Эта технология построена по аналогии с принципами работы зрительной коры головного , в которой были открыты так называемые простые клетки, реагирующие на прямые линии под разными углами, и сложные клетки, реакция которых связана с активацией определённого набора простых клеток. Таким образом, идея сверточных нейронных сетей заключается в чередовании сверточных слоев (англ. convolution layers) и субдискретизирующих слоев (англ. subsampling layers, слоёв подвыборки).[6]
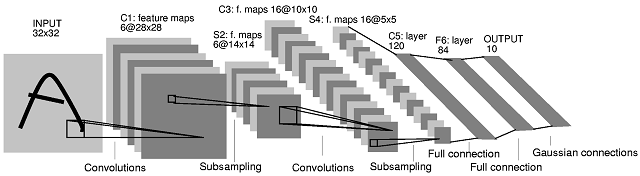
Рис 1. Архитектура сверточной нейронной сети
Ключевым моментом в понимании сверточных нейронных сетей является понятие так называемых «разделяемых» весов, т.е. часть нейронов некоторого рассматриваемого слоя нейронной сети может использовать одни и те же весовые коэффициенты. Нейроны, использующие одни и те же веса, объединяются в карты признаков (feature maps), а каждый нейрон карты признаков связан с частью нейронов предыдущего слоя. При вычислении сети получается, что каждый нейрон выполняет свертку (операцию конволюции) некоторой области предыдущего слоя (определяемой множеством нейронов, связанных с данным нейроном). Слои нейронной сети, построенные описанным образом, называются сверточными слоями. Помимо, сверточных слоев в сверточной нейронной сети могут быть слои субдискретизации (выполняющие функции уменьшения размерности пространства карт признаков) и полносвязные слои (выходной слой, как правило, всегда полносвязный). Все три вида слоев могут чередоваться в произвольном порядке, что позволяет составлять карты признаков из карт признаков, а это на практике означает способность распознавания сложных иерархий признаков [3].
Что же именно влияет на качество распознавания образов при обучении сверточных нейронных сетей? Озадачившись данным вопросом, наткнулись на статью Мэттью Зайлера (Matthew Zeiler). Он разработал концепцию и технологию Deconvolutional Neural Networks (DNN) для понимания и анализа работы свероточных нейронных сетей. В статье Мэттью Зайлера предлагается технология Deconvolutional Neural Networks, которая осуществляет построение иерархических представлений изображения (рис 2), с учетом фильтров и параметров, полученных при обучении CNN (Рис 2). Эти представления могут быть использованы как для решения задач первичной обработки сигналов, таких как шумоподавление, а также они могут обеспечивать низкоуровневые функции для распознавания объектов. Каждый уровень иерархии может формировать более сложные функции на основе функций уровней, расположенных в иерархии ниже.
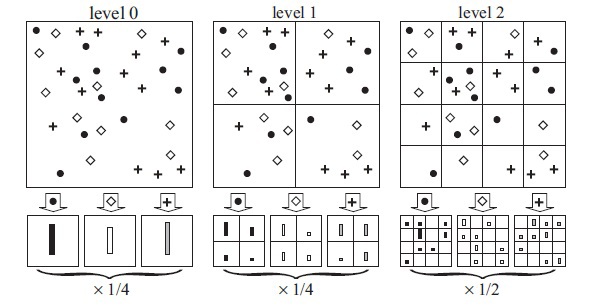
Рис 2. Представления изображений
Основным различием между CNN и DNN является то, что в CNN входной сигнал подвергается нескольким слоям свертки и субдискретизации. DNN наоборот стремится сгенерировать входной сигнал в виде суммы сверток карт признаков с учетом применяемых фильтров (Рис 3). Для решения данной задачи, используется широкий спектр инструментов теории распознавания образов, например алгоритмы устранения размытости (deblurring). Работа, написанная Мэттью Зайлером, является попыткой связать распознавание объектов изображения с низкоуровневыми задачами и алгоритмами обработки и фильтрации данных.
Для понимания операции свертки требуется интерпретация поведения карт признаков в промежуточных слоях. Для исследования сверточной нейронной сети, DNN прикрепляется к каждому из его слоев, как показано на рис.3, обеспечивая непрерывный путь от выходов сети к входным пикселям изображения. Сначала, над входным изображением выполняется операция свертки и по всем слоям вычисляются карты признаков, после чего для изучения поведения в CNN устанавливаются значения весов всех нейронов в слое равными нулю и полученные карты признаков используются в качестве входных параметров для прилагаемого deconvnet слоя. Тогда мы последовательно выполняем операции: (I) разъединения, (II) ректификация и (III) фильтрация. Карты признаков в слое ниже реконструируются таким образом, чтобы получить необходимые параметры, такие как веса нейронов в слое и применяемые фильтры. Данная операция повторяется до тех пор, пока не будут достигнуты значения входных пикселей изображения.
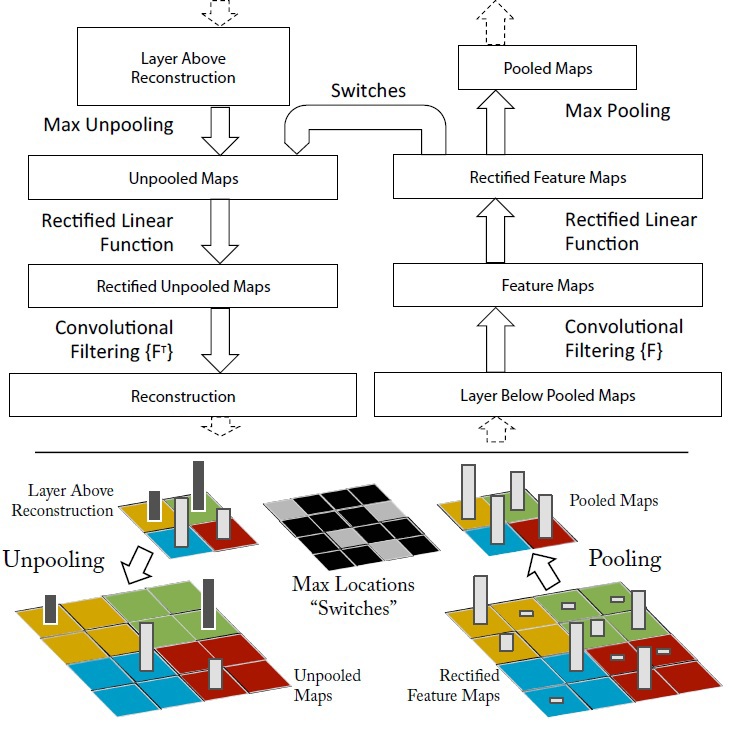
Рис 3. Процесс исследования сверточных нейронных сетей с использованием DNN
Операция разъединения: в сверточных нейронных сетях, это операция объединения, она является необратимой, однако можно получить приближенное обратное значение путем записи местоположения максимумов в пределах каждой области. Под операцией объединения понимается суммирование всех входных значений нейрона и передача полученной суммы в передаточную функцию нейрона. В DNN, операция разъединения использует изменения в наборе переменных, размещенных в слое выше, в соответствующих местах в слое, который обрабатывается в данный момент (см. рис 2).
Операция ректификация: сверточная нейронная сеть использует нелинейную функцию (relu(x)=max(x,0), где x-входное изображение), обеспечивая тем самым то, что полученные карты признаков всегда будут положительными.
Операция фильтрация: сверточная нейронная сеть использует полученные в процессе обучения сети фильтры для свертки карт признаков из предыдущего слоя. Чтобы понять какие фильтры были применены к изображению, deconvnet использует транспонированные версии тех же фильтров. Проектирование “спуска вниз” с более высоких уровней использует изменения параметров, полученных при обучении CNN. Поскольку эти изменения свойственны данному входному изображению, реконструкция, полученная из одной функций, таким образом, напоминает маленький кусочек начального изображения со структурами (рис 4), взвешенными в соответствии с их вкладом в карту признаков. Так как модель обучается в соответствии с выявленными признаками, они, структуры, неявно показывают, какие части входного изображения (или части двух разных изображений) являются отличающимися по полученным признакам[4]. Также, полученные структуры позволяют делать выводы о том, какие низкоуровневые признаки изображения являются ключевыми для его классификации.

Рис. 4. Структуры изображения.
Хотя в теории глобальный минимум всегда можно найти, на практике это сложно. Это связано с тем, что элементы в картах признаков соединены друг с другом через фильтры. Одним элементом в карте могут быть затронуты другие элементы, расположенные далеко от данного элемента, а это означает, что минимизация может занять очень много времени.
Преимущества использования DNN:
1) концептуально простые схемы обучения. Обучение DNN производится за счет использования unpooling, ректификации и фильтрации изображения, так же используются карты признаков, полученные при обучении CNN;
2) применяя DNN к исходным изображениям, можно получить большой набор фильтров, которые охватывают всю структуру изображения, используя примитивные представления; Таким образом, получаются фильтры, применяемые ко всему изображению, а не к каждому маленькому кусочку исходного изображения. Это является большим преимуществом, так как появляется более полное понимание процессов происходящих при обучении CNN.
3) представления (рис.2) можно получить без настройки особых параметров или дополнительных модулей, таких как разъединение, ректификация и фильтрация. Они, представления, получаются в ходу обучения CNN;
4) подход с использованием DNN основан на методе поиска глобального минимума, а также использовании фильтров полученных при обучении CNN, и предназначен для сведения к минимуму плохо обусловленных затрат, которые возникают в сверточном подходе.
В обозреваемой статье приводятся также результаты экспериментов, проводимых Метью Зайлером. Сеть, предложенная им на соревнованиях ImageNet 2013, показала наилучший результат при решении задачи классификации изображений, ошибка составила всего 14,8%. Классификация объектов 1000 категорий. Обучающая выборка состояла из 1,2 миллионов изображений, а тестовая — из 150 тысяч изображений. Для каждого тестового изображения алгоритм распознавания должен выдать 5 меток классов в порядке убывания их достоверности. При подсчете ошибки учитывалось, соответствует ли наиболее достоверная метка с известной для каждого изображения меткой класса объекта, действительно присутствующего на изображении. Использование 5 меток задумано для того, чтобы исключить «наказание» для алгоритма в случае, когда он распознал на изображении объекты других классов, которые могут быть представлены в неявном виде[1]. Подробнее соревнования по ImageNet 2013 описаны здесь.
Результаты работы Deconvolution Neural Networks приведены на рисунке 5.
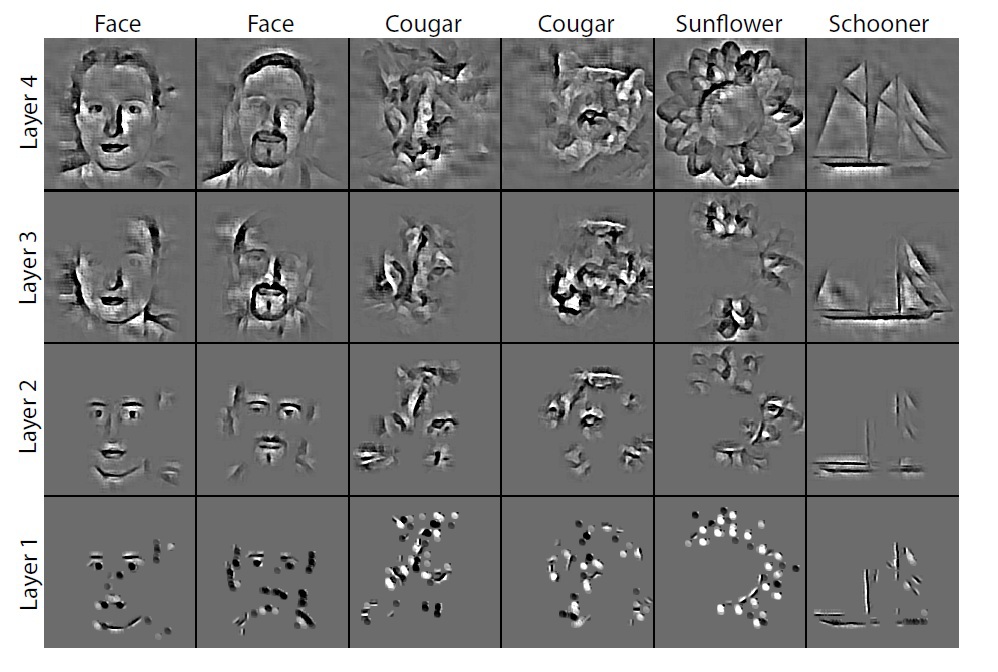
Рис 5. Результаты работы DNN
Зайлер в дальнейшем планирует развивать технологию DNN в следующих направлениях:
1) усовершенствование классификации изображений в DNN. DNN сети были введены для того, чтобы понять особенности процесса обучения сверточных сетей. Используя параметры, полученные в ходе обучения сверточной нейронной сети, в дополнение к функциям высокого уровня можно обеспечить механизм для повышения уровня классификации в DNN. Дальнейшая работа связана с классификацией исходных изображений, таким образом можно сказать, что будет применен шаблонный метод. Изображения будут классифицироваться, основываясь на классе, к которому принадлежит объект.
2) масштабирование DNN. Методы вывода, используемые в DNN, по своей природе работают медленно, так как необходимо выполнение множества итераций. Так же должны быть исследованы численные методы аппроксимации, основанные на прямой связи. Это потребует только те функции и параметры объединения для текущей партии снимков, которые позволяют DNN масштабироваться до больших наборов данных.
3) усовершенствование сверточных моделей для обнаружения нескольких объектов на изображении. Сверточные сети, как известно, используются для классификации в течение многих лет и в последнее время они были применены к очень большим наборам данных. Однако, необходима дальнейшая разработка алгоритмов, используемых в сверточном подходе для обнаружения сразу нескольких объектов, присутствующих на изображении. Для обнаружения CNN сразу нескольких объектов на изображении требуется большой набор тренировочных данных, так же значительно увеличивается количество параметров для обучения нейронной сети.[4]
Изучив его статью, решили провести исследование по DNN. Метью Зайлер разработал Deconvolutional Network Toolbox для Matlab. И сразу же столкнулись с проблемой – нетривиальной задачей установки данного Toolbox. После успешной установки, решили поделиться этим навыками с хабравчанами.
Итак, перейдем к процессу установки. Deconvolutional Network Toolbox устанавливался на компьютер со следующими техническими характеристиками:
• Windows 7 64x
• Matlab b2014a
Начнем с подготовки программного обеспечения, которое необходимо установить:
1) Windows SDK, при установке необходимо убрать галочки с пунктов Visual C++ Compilers
Microsoft Visual C++ 2010
Если на компьютере уже установлена VS 2010 redistributable x64 или VS 2010 redistributable x86, то её придется удалить.
Завершаем процесс установки Windows SDK, и устанавливаем патч
2) После этого скачиваем и устанавливаем VS 2010
3) Так же для установки данного тулбокса необходимо установить icc компилятор, в нашем случае это Intel C++ Composer XE Compiler 2011.
4) В Matlab набрать команду
mbuild -setup
и автоматически выберется SDK 7.1.
Аналогично происходит с
mex –setup
Если компилятор был успешно установлен, то теперь можно приступить к сборке тулбокса.
Подготовка программного обеспечения завершена. Приступаем к процессу компиляции.
1) Скачать тулбокс с
www.matthewzeiler.com/software/DeconvNetToolbox/DeconvNetToolbox.zip и распаковать
2) В Matlab заходим в директорию, где находится распакованный тулбокс, и запускаем файл «setupDeconvNetToolbox.m»
3) Заходим в папку PoolingToolbox. Открываем файл compilemex.m
В этот файл необходимо внести ряд изменений, так как он написан для Linux.
Необходимо прописать пути в MEXOPTS_PATH к Matlab, к библиотекам находящимся в папке с компилятором для 64х битной системы, а так же к заголовочным файлам компилятора и VisualStudio 2010.
4) Внесем еще несколько изменений, выглядят они так
exec_string = strcat({'mex '},MEXOPTS_PATH,{' '},{'-liomp5mt max_pool.cpp'});
eval(exec_string{1});
Аналогично нужно сделать и для остальных компилируемых файлов.(Пример)
5) Внесем так же изменения в mexopts.sh
Там необходимо так же прописать пути к 64 и 32х битному компилятору. (Пример)
6) Теперь переходим в директорию IPP Convolution Toolbox
7) Заходим в папку MEX и запускаем файл complimex.m, тут тоже необходимо прописать тоже, что и в 4 пункте, и отдельно дописать пути к ipp_lib и ipp_include. (Пример)
Matlab скажет что не хватает библиотек, их необходимо положить в c:Program Files (x86)IntelComposerXE-2011ipplibintel64
8) Аналогично п5 вносим изменения
exec_string = strcat({'mex '},MEXOPTS_PATH,{' '},{IPP_INCLUDE_PATH},{' '}, {IPP_LIB64_PATH},{' '},{IPP_LIB_PATH},{' '},{'-liomp5mt -lippiemerged -lippimerged -lippcore -lippsemerged -lippsmerged -lippi ipp_conv2.cpp'});
eval(exec_string{1});
(Пример)
Запускаем файл, если все заработало корректно – продолжаем.
9) Заходим в папку GUI
10) Открываем файл gui.m, тут необходимо прописать пути к папке с распакованным Deconvolutional toolbox, у меня это выглядит так
START_DATASET_DIRECTORY = 'C:/My_projects/DeconvNetToolbox/DeconvNetToolbox';
START_RESULTS_DIRECTORY = 'C:/My_projects/DeconvNetToolbox/DeconvNetToolbox';
(Пример)
11) Запускаем файл gui.m. Заработало? Закрываем и идем дальше.
12) Теперь в папке, куда выкачали Тулбокс, создаем папку Results, а в ней папку temp. Запускаем теперь из папки Results gui.m, появляется графический интерфейс, в котором задаются параметры, в нижнем правом углу «Save Results» устанавливаем равным 1, и нажимаем «Save». В результате этих действий в директории GUI сгенерируется файл gui_has_set_the_params.mat с параметрами демонстрационной модели DNN сети, предложенной Метью Зайлером.
13) Теперь можно приступать к обучению полученной модели посредством вызова скрипта trainAll.m.
Если все действия были выполнены правильно, то после завершения обучения в папке Results можно будет увидеть результат работы.
Теперь можно начинать проводить исследования! Результатам исследований будет посвящена отдельная статья.
Список литературы:
1) habrahabr.ru/company/nordavind/blog/206342/
2) habrahabr.ru/company/synesis/blog/238129/
3) habrahabr.ru/post/229851/
4) www.matthewzeiler.com/pubs/
5) geektimes.ru/post/74326/
6) nordavind.ru/node/550
Автор: Nordavind

