27 мая завершился первый этап олимпиады Mail.Ru Group по программированию Russian Code Cup 2012. Всего в RCC’12 приняло участие более тысячи человек, из которых 200 лучших вышло в полуфинал соревнования, в отборочный раунд. Победителем первого квалификационного раунда стал студент мехмата ННГУ Владислав Епифанов из Нижнего Новгорода. Участниками было направлено 3391 решение, из которых 1066 были приняты системой как верные. 634 человека или 63% от общего числа участников, решили хотя бы одну задачу.
Russian Code Cup — индивидуальное соревнование по спортивному программированию, ежегодно проводимое Mail.Ru Group. Оно традиционно состоит из трех этапов: в начале лета проходят три квалификационных раунда, затем лучшие принимают участие в отборочном туре, первые пятьдесят победителей отборочного тура соревнуются в финале. Личного присутствия потребует только последний из них, остальные же проводятся онлайн. Все финалисты будут отмечены ценными подарками, а приз участнику, занявшему первое место, составит 10 000 долларов. За второе и третье место полагаются 5 000 и 3 000 долларов.
В статье я расскажу о задачах, которые предлагались участникам и о способах их решения. Краткий разбор задач опубликован на сайте сразу после завершения RCC, тут же я постараюсь разъяснить подробности настолько, чтобы решение было понятно даже начинающим программистам.
Всего на тур было предложено пять задач: «Параллелепипед», «Перестройка», «Война», «Этикетка», «Джавайское оружие».
«Параллелепипед»
Задача «Параллелепипед» заключалась в том, чтобы по известным длинам двенадцати спичек проверить, можно ли из них склеить каркас параллелепипеда. Эта задача была самой простой и с нее начали решение все участники.
Тут следовало вспомнить, что параллелепипед — это фигура, основанием которой служит параллелограмм — четырехугольник, у которого стороны попарно параллельны. У параллелепипеда есть три размерности в 12 ребрах — длина, ширина и высота. Следовательно, необходимо ответить на вопрос, есть ли среди входных данных ровно три группы по четыре одинаковых числа.
Чтобы понять это, необходимо отсортировать все числа и убедиться, что получилось три группы по четыре одинаковых числа (одинаковых по крайней мере внутри каждой группы). Если это так, выводить yes, иначе — no.
#include <iostream>
#include <cstdio>
using namespace std;
int main()
{
int a[12];
while (true)
{
bool ex = true;
for (int i = 0; i < 12; i++)
cin >> a[i];
for (int i = 0; i < 12; i++)
if (a[i] != 0) ex = false;
if (ex) break;
bool ans = true;
for (int i = 0; i < 12; i++)
{
int k = 0;
for (int j = 0; j < 12; j++)
k += (a[i] == a[j]);
if (k % 4 != 0) ans = false;
}
cout << ((ans) ? "yes" : "no") << endl;
}
}
Попыток сдать задачу «Параллелепипед» было 1479, из которых 639 – успешных (43%). Эта задача оказалась наиболее доступной – число попыток более чем в два раза больше, чем на других задачах, высокий процент успешности.
RussianCodeCup.Ru: постановка задачи
RussianCodeCup.Ru: разбор задач
«Перестройка»
Вторая задача была посложнее.
По условиям задачи существовало множество дорог между городами. Между любыми двумя городами проложено не более одной дороги. В результате некой дорожной реформы одна из существующих дорог должна была быть разрушена, а другая, из не проложенных ранее, должна была быть построена, причем таким образом, чтобы в итоге из любого города в любой можно было доехать (изначально это могло быть не так). Также есть уточнение, что дорога не может вести из города в него же. Необходимо было посчитать количество вариантов реализации этой реформы.
Эта задача предполагает некоторые знания из области теории графов. Вершинами у нашего графа являются города, ребрами — дороги. В теории графов есть понятие связности графа — наличия пути из любой вершины в любую. В данном случае изначально мы имеем граф неизвестной связности, а в итоге должны получить граф обязательно связный. Есть понятие компоненты связности графа — это максимальное по включению множество связанных между собой вершин. Соответственно число компонент связности — это количество несвязанных между собой групп вершин. Например, в случае, если ребер графа (=дорог) нет вообще, число компонент связности равна количеству вершин (=городов). Также введем понятие «моста» — ребра, удаление которого делает граф несвязным, то есть делит его на несвязанные части.
Итак, вспомним суть реформы из постановки задачи: одно существующее ребро (=дорога) удаляется, и добавляется другое в место, где его раньше ребра не было. Нужно посчитать число вариантов такой реформы.
Также по условиям задачи помним, что наша реформа должна приводить к связному графу, т.е. с одной компонентой связности. Изначально количество групп несвязных между собой городов-вершин может быть любым.
Очевидно, что при числе компонент связности более двух сделать в итоге связный граф добавлением одного ребра у нас никак не получится, ведь так мы свяжем только две группы между собой, а их — больше. Вот иллюстрация этого варианта:
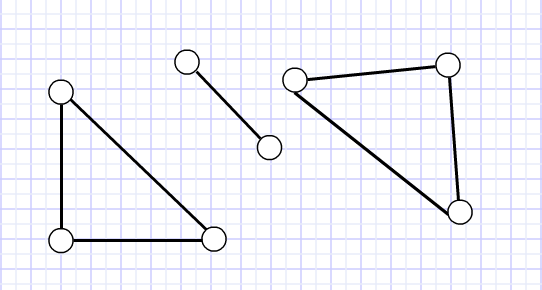
Следовательно, в этом простейшем случае ответ — ноль вариантов.
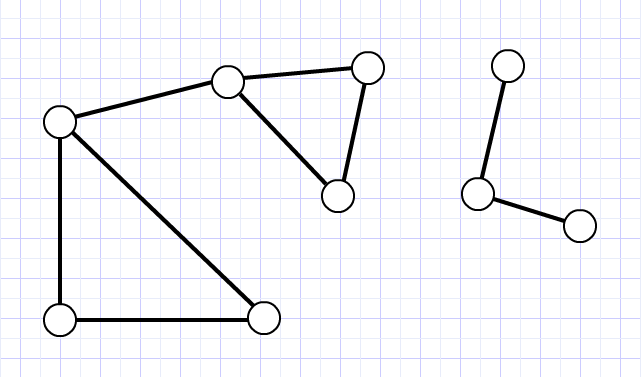
В случае, если мы имеем дело с двумя группами, то есть компонент связности две, то количество вариантов рассчитывается следующим образом.
Сначала нужно найти, какие ребра являются «мостами» — ведь при удалении этих ребер мы приводим все к первому, рассмотренному выше варианту. Добавить их же назад мы не можем, так как по условиям задачи добавить можно только там, где ребер не было. Поскольку в итоге мы должны получить связный граф, добавленное ребро должно соединять вершины из разных компонент связности — делать из несвязного графа связный. Две группы из N и M вершин можно связать между собой NxM способами. Следовательно, число реформ у нас получится NxMxC, где C = число ребер без учета тех из них, что являются мостами.
Третий случай, когда мы имеем изначально связный граф — самый сложный. В этом случае компонента связности одна, но некоторые ребра могут являться мостами. В итоге число вариантов реформ является суммой двух слагаемых: первое — число вариантов удаления ребер-не-мостов, второе – число вариантов удаления ребер-мостов.
Общее количество ребер можно посчитать по числу вершин: n * (n-1))/2 (где n = число вершин). Количество ребер, которые можно добавить, вычисляется вычитанием из общего количества числа имеющихся ребер. Так мы получаем первое слагаемое — число ребер, не являющихся мостами, помноженное на число ребер, которые можно добавить.
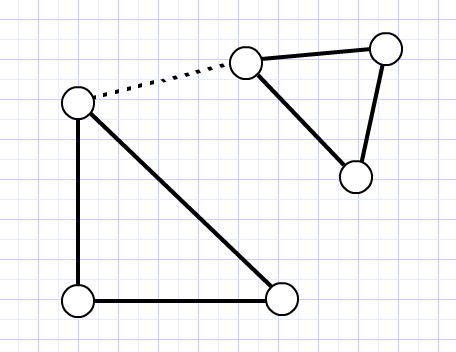
При удалении «моста» мы должны соединить ребром две получившиеся компоненты связности, развязанные группы вершин. Количество способов это сделать равно произведению вершин справа от моста на количество вершин слева от моста, уменьшенное на единицу, так как сам мост обратно мы поставить не можем по условию задачи.
В итоге для решения этой задачи необходимо знание следующих алгоритмов из теории графов:
- подсчет количества компонент связности;
- нахождение мостов;
- подсчет количества вершин с каждой стороны от моста.
Нахождение количества компонент связности
Для решения можно применить алгоритм обхода в глубину. Принцип простой — обходим рекурсивно все вершины, помечая их как посещенные. Как только обошли все, переходим к первой же, которую еще не посетили, если таковая существует, одновременно увеличивая на единицу число компонент связности. И так до тех пор, пока не кончатся все вершины.
Описание алгоритма и пример: e-maxx.ru/algo/connected_components
Нахождение мостов
Алгоритм нахождения мостов основывается на поиске «циклов» — альтернативных путей между вершинами. Если такого пути не обнаруживается, то ребро является мостом.
Описание алгоритма и пример: e-maxx.ru/algo/bridge_searching
Этот алгоритм можно модифицировать, чтобы находить число вершин с разных сторон от моста.
Попыток сдать задачу «Перестройка» было 621, из которых 137 – успешных (22%).
RussianCodeCup.Ru: постановка задачи
RussianCodeCup.Ru: разбор задач
решение на C++ (pastebin)
«Война»
«На одну маленькую нефтеносную страну было совершено нападение высокотехнологичной армией другой враждебной страны. Для защиты была мобилизована армия, состоящая из n солдат. Перед началом решающего боя все n солдат выстроились в шеренгу перед генералом. Он всегда считал, что все солдаты в его войске одинакового роста, однако это оказалось не так. Генерал понял, что такая армия малоэффективна, и решил разбить ее на подразделения. Под подразделениями генерал подразумевал непустые группы солдат, стоящих друг за другом в шеренге. Также генерал решил ввести понятие «мощность подразделения», которое определялось как:
- количество солдат в подразделении, если в шеренге они стоят в порядке невозрастания или неубывания их роста;
- 0 в противном случае.
Также генерал решил, что мощность армии равна произведению мощностей всех подразделений.
Генерал хочет найти такое разбиение армии на подразделения, чтобы мощность всей армии была максимальна. Помогите ему решить эту задачу»
Фактически задача сводится к разбиению массива чисел на монотонные отрезки так, чтобы произведение их длин было максимально. Понятно, что если большой отрезок можно разделить на несколько подотрезков, то произведение длин будет больше, чем длина большого отрезка. Это можно сделать при длине отрезка больше трех: если n ≥ 4, то 2(n — 2) = 2n — 2 ≥ n.
Теперь можно решить задачу с помощью динамического программирования — для каждого префикса необходимо посчитать оптимальный ответ и то, какую длину имеет последний отрезок на этом префиксе.
Для этого необходимо перебрать, какой длины отрезок нужно взять (1, 2 или 3), проверить, что на нем последовательность не возрастает или не убывает, и выбрать из подходящих вариантов максимум.
Для восстановления ответа нужно воспользоваться стандартной идеей: восстанавливать с конца, пользуясь информацией об оптимальной длине последнего отрезка для данного префикса.
Попыток сдать задачу «Война» было 879, из которых 184 – успешных (21%).
RussianCodeCup.Ru: постановка задачи
RussianCodeCup.Ru: разбор задач
решение на C++ (pastebin)
«Джавайское оружие»
«С древности у каждого джавая был набор из трех видов оружия: лазерный меч, лазерная сабля и лазерный ножик для намазывания масла на хлеб (вдруг джавай проголодается).
Но так как это оружие джавайское, а не простое, на длины входящих в набор предметов накладывались следующие ограничения:
Длина ножика — d1, длина сабли — d2, длина меча — d3 должны быть простыми числами;
- d1 ≤ d2 ≤ d3;
- (d1 + d2)2 − 1 делится на d3;
- (d2 + d3)2 − 1 делится на d1;
- (d3 + d1)2 − 1 делится на d2.
Компания «Dart Generics Industries» продает любой набор джавайского оружия по его номеру в лексикографическом порядке. А именно, упорядочим все джавайские наборы по неубыванию d1, при равном d1 по неубыванию d2, а при равных d1 и d2 по возрастанию d3 и пронумеруем их в этом порядке от 1 до бесконечности. Тогда по заданному k можно купить k-й набор в этом порядке.
Джавай Anykey хочет купить k-й набор. Подскажите ему размеры его оружия»
Покажем, что из условий, наложенных на длины оружия, следует, что d1 = d2. Пусть никакие три числа не равны, тогда d1 < d2 < d3. По условию (d1 + d2)2 − 1 = (d1 + d2 + 1)(d1 + d2 — 1) делится на d3, так как d3 простое, один из множителей делится на d3.
Пусть, например, (d1 + d2 + 1) делится на d3. Из условия d1 < d2 < d3 следует, что d1 + d2 + 1= d3. Но тогда (d2 + d3)2-1 = (2d2 + d1 + 1)2-1 = 4d22 + 4d2 + 4d1d2 + d12 + 2d1. По условию это число делится на d1, значит 4d22 + 4d2 делится на d1. Значит либо d1 = 2, либо d1 = d2, либо d1 = d2+1.
Применяя аналогичные рассуждения к третьему условию, получаем, что либо d2 = 2, либо d1 = d2, либо d2 = d1+1. Из всех пар этих условий совместны только d1=d2 и d1=2, d2=3. Но в последнем случае подобрать подходящее d3 не удается. Значит d1=d2.
Аналогично рассматривается случай (d1 + d2 — 1) делится на d3.
Обозначим d1=d2 как p. Следовательно (p + p)2-1 = (2p — 1)(2p+1) делится на d3, а так как оно простое и наибольшее, оно может быть равно только (2p-1) или (2p+1). Следовательно, все тройки должны иметь вид (p,p,2p-1) или (p,p,2p+1). Поскольку по условиям задачи первое простое число находится в числе первых 60000 тысяч, оно не превышает 107. Следовательно, при таких ограничениях можно применить решето Эратосфена — алгоритм поиска простых чисел.
Решето Эратосфена
Принцип алгоритма поиска простых чисел «по Эратосфену» заключается в следующем. К примеру нужно найти простые числа в промежутке от 1 до некоторого N <= 107. Создаем массив на N элементов и заполняем его значением «true». Затем последовательно проходим по нему до корня из N, и везде, где встречаем true, вычеркиваем все кратные ему числа до N. На первом шаге вычеркиваются все четные числа (потому что первое простое — 2), на втором — все кратные тройке и т.д.
Описание алгоритма и пример: http://habrahabr.ru/post/91112/
Попыток сдать задачу «Джавайское оружие» было 303, из которых 126 – успешных (42%).
RussianCodeCup.Ru: постановка задачи
RussianCodeCup.Ru: разбор задач
решение на C++ (pastebin)
«Этикетка»
Пожалуй, эта задача была самой сложной из всех, хотя объяснение у нее, вероятно, одно из самых простых.
«При археологических исследованиях порой находятся крайне интересные вещи. Так, например, при раскопках поселения одной древней цивилизации было выяснено, что ее представители, так же как и современные люди, пили напитки из бутылок, на которые были наклеены этикетки с информацией про напиток, содержащейся в бутылке. Одна из таких этикеток даже сохранилась до наших дней. Однако перед учеными, занимавшимися расшифровкой, совершенно неожиданно появилась крайне интересная проблема.
Проблема заключалась в том, что эта цивилизация не пользовалась знаком переноса. Как только строка заканчивалась, чтение просто продолжалось со следующей строки. При расшифровке книг это не доставляло никаких неудобств, однако у этикетки есть существенное отличие от книги — этикетка наклеивалась на бутылку так, что получался цельный цилиндр, на котором по кругу был написан текст. При чтении текста следовало начать читать первую строку от места склейки, после достижения места склейки перейти на вторую строку, после этого на третью и так далее. Но ученым пока не удается определить место, где этикетка была склеена! Так что вместо текста пока имеется только набор строк одинаковой длины k, состоящих из букв и символов «.», которые использовались этой цивилизацией вместо пробелов.
К счастью, кроме самой этикетки имеется словарь, в котором перечислены все возможные слова, которые использовались этой цивилизацией. Теперь по этим данным вам необходимо определить, сколько существует вариантов местонахождения склейки. Более формально, вам необходимо определить, сколько существует неотрицательных значений t < k таких, что конкатенация всех данных вам строк, циклически сдвинутых влево на t символов, представляет собой набор слов из словаря, разделенных одним или несколькими символами «.». Кроме этого, вам необходимо также вывести все эти значения t.
Для того, чтобы решить эту задачу, следует перейти от понятия строк и символов к массивам значений и числам — это сильно упростит решение и позволит уложится в ограничения по времени и памяти.
Ключевой идеей в решении этой задачи является выбор полиномиального хеширования для кодирования слов. Это позволит перейти от работы со строками в работу с массивами и числами, что заметно быстрее.
Полиномиальный хеш от строки рассчитывается как сумма произведений кода i-го символа на n в степени i. Такие хеши часто используются для ускорения операций поиска подстроки в строке: если две строки составляют третью, то их хэши находятся в простой арифметической зависимости H3 = H1 + k*H2, где k = основание хеша, возведенное в степень длины первой строки.
В данном случае используем методику расчета хеша, где номер позиции будет отсчитываться с конца строки. Это понадобится для пересчета хеша при циклическом сдвиге влево.
Для начальной позиции можно легко вычислить хеши всех слов, с учетом переносов слов со строки на строку.
Теперь нужно произвести циклический сдвиг на одну позицию влево. Для этого придется пересчитать хеши пограничных слов: из хеша левого слова вычесть код уходящего символа, помноженный на основание хеша в степени длины строки, правый хеш дополнить кодом этого символа, умноженного на основание хэша.
Важно, что проверять все хеши из всех списков на наличие в словаре будет непросто, из-за ограничений на время работы. Поэтому проверки здесь следует «кэшировать» — проверять только те слова, которые могут измениться — все пограничные слова.
Полиномиальные хеши
Описание алгоритма: http://habrahabr.ru/post/142589/
Попыток сдать задачу «Этикетка» было 109, из которых всего 6 – успешных (5%). Эта задача оказалась наиболее сложной для участников.
RussianCodeCup.Ru: постановка задачи
RussianCodeCup.Ru: разбор задач
решение на C++ (pastebin)
Напоминаем, что следующий тур состоится в это воскресенье, 2 июня, в 11:00. Необходима предварительная регистрация. Задачи каждого следующего тура, вероятно, будут попроще, но количество попыток попасть в отборочный становится все меньше. Торопитесь!
Алиев Рауф
директор по исследованиям и образованию
руководитель проекта Russian Code Cup
Mail.Ru Group
Автор: raliev
