Мне интересна обработка изображений, в особенности работа с особыми точками. Ища информацию по детекторам углов, я не нашел достаточно большого обзора этих алгоритмов на русском языке. Поэтому я решил исправить ситуацию, написав эту статью. План статьи следующий:
- Введение
- Свойства особых точек
- Детекторы углов
- Moravec
- Harris
- Shi-Tomasi
- Förstner
- SUSAN
- Trajkovic
- FAST
- CSS
- Детектор, основанный на глобальных и локальных свойствах кривизны
- CPDA
- Выводы

Введение
Для выделения из изображения некоторой интерпретируемой информации необходимо привязаться к локальным особенностям изображения. На изображении возможно выделить особые точки. Особая точка m, или точечная особенность (англ. point feature, key point, feature), изображения – это точка изображения, окрестность которой o(m) можно отличить от окрестности любой другой точки изображения o(n) в некоторой другой окрестности особой точки o2(m). В качестве окрестности точки изображения для большинства алгоритмов берётся прямоугольное окно, составляющее размер 5x5 пикселей. Процесс определения особых точек достигается путём использования детектора и дескриптора.
Детектор – это метод извлечения особых точек из изображения. Детектор обеспечивает инвариантность нахождения одних и тех же особых точек относительно преобразований изображений.
Дескриптор – идентификатор особой точки, выделяющий её из остального множества особых точек. В свою очередь, дескрипторы должны обеспечивать инвариантность нахождения соответствия между особыми точками относительно преобразований изображений [1].
Свойства особых точек
В 1992 Haralick и Shapir [10] выделили следующие требования к особым точкам в виде следующих свойств:
- Отличимость (distinctness) – особая точка должна явно выделяться на фоне и быть отличимой (уникальной) в своей окрестности.
- Инвариантность (invariance) – определение особой точки должно быть независимо к аффинным преобразованиям.
- Стабильность (stability) – определение особой точки должно быть устойчиво к шумам и ошибкам.
- Уникальность (uniqueness) – кроме локальной отличимости, особая точка должна обладать глобальной уникальностью для улучшения различимости повторяющихся паттернов.
- Интерпретируемость (interpretability) – особые точки должны определяться так, чтобы их можно было использовать для анализа соответствий и выявления интерпретируемой информации из изображения.
Интересно, что в [5] Tuytelaars и Mikolajczyk (2006) выделили следующие свойства, которыми должны обладать особые точки:
- Повторяемость (repeatability) – особая точка находится в одном и том же месте сцены или объекта изображения, несмотря на изменения точки обзора и освещённости.
- Отличительность / информативность (distinctiveness/informativeness) – окрестности особых точек должны иметь большие отличия друг от друга, так, чтобы возможно было выделить и сопоставить особые точки.
- Локальность (locality) – особая точка должна занимать небольшую область изображения, чтобы быть уменьшить вероятность чувствительности к геометрическим и фотометрическим искажениям между двумя изображениями, снятых в различных точках обзора.
- Количество (quantity) – число обнаруженных особых точек должно быть достаточно большим, так чтобы их хватило для обнаружения даже небольших объектов. Однако оптимальное количество особых точек зависит от предметной области. В идеале количество обнаруженных особых точек должно адаптивно определяться с использованием простого и интуитивного порога. Плотность расположения особых точек должна отражать информационное содержимое изображения, чтобы обеспечить его компактное представление.
- Точность (accuracy) – обнаруженные особые точки должны точно локализовываться, как в исходном изображении, так и взятом в другом масштабе.
- Эффективность (efficiency) – время обнаружения особых точек на изображении должно быть допустимым в критичных по времени приложениях.
В целом, эти свойства пересекаются с [10], но по-разному интерпретируются.
Детекторы углов
Существуют множество алгоритмов определения особых точек, предназначенных для разных областей применения. В этой статье я уделяю внимание детекторам углов (или как еще их называют уголковым детекторам).
Углы (corners) – особые точки, которые формируются из двух или более граней, и грани обычно определяют границу между различными объектами и / или частями одного и того же объекта. [2] По-другому можно сказать, что углы – это точка, у которой в окрестности интенсивность изменяется относительно центра (x,y). Углы определяются по координатам и изменениям яркости окрестных точек изображения. Главное свойство таких точек заключается в том, что в области вокруг угла у градиента изображения преобладают два доминирующих направления, что делает их различимыми. Градиент – векторная величина, показывающая направление наискорейшего возрастания функции интенсивности изображения I(x,y). Так как изображение дискретно, то вектор градиента определяется через частные производные по оси x и y через изменения интенсивностей соседних точек изображения. Большинство методов рассматривают угловатость, зависящую от производной 2-го порядка, поэтому в общем методы чувствительны к шуму.
В зависимости от количества пересекаемых граней существуют разные виды уголков: L-, Y- (или T-), и X- связные [3] (некоторые выделяют еще стреловидно связные углы [2]). Различные уголковые детекторы по-разному реагируют на каждый из таких видов уголков.

Подходы к определению особых точек могут быть разделены на 3 категории [10]:
- Основанные на интенсивности изображения: особые точки вычисляются напрямую из значений интенсивности пикселей изображения.
- Использующие контуры изображения: методы извлекают контуры и ищут места с максимальным значением кривизны или делают полигональную аппроксимацию контуров и определяют пересечения. Эти методы чувствительны к окрестностям пересечений, поскольку извлечение часто может быть неправильным в тех местах, где пересекаются 3 или более краев.
- На основе использования модели: используются модели с интенсивностью в качестве параметров, которые подстраиваются к изображениям-шаблонам до субпиксельной точности. Имеют ограниченное применение с особыми точками специальных видов (например, L-связными углами), зависят от используемых шаблонов.
На практике для широкого применения наиболее распространены методы, основанные на интенсивности изображения.
Далее я рассмотрю описания основных детекторов особых точек, определяющих углы. Затем будет представлена сравнительная таблица детекторов с выводами об их применимости к различным ситуациям и, наконец, изображения с примененными к ним уголковыми детекторами.
Moravec
Работа в исследовании привязки изображений с использованием особых точек началась детектора Моравеца (Moravec, 1977). Детектор Моравеца – самый простой из существующих. Автор рассматривает изменение яркости квадратного окна W (обычно размера 3х3, 5х5, 7х7 пикселей) относительно интересующей точки при сдвиге окна W на 1 пиксель в 8-ми направлениях (горизонтальных, вертикальных и диагональных) [4]. Алгоритм:
- Для каждого пикселя (x,y) в изображении вычислить изменение интенсивности
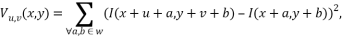
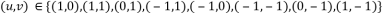
- Построить карту вероятности нахождения углов в каждом пикселе (x,y) изображения посредством вычисления оценочной функции
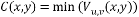 . То есть определяется направление, которому соответствует наименьшее изменение интенсивности, т.к. угол должен иметь смежные ребра.
. То есть определяется направление, которому соответствует наименьшее изменение интенсивности, т.к. угол должен иметь смежные ребра. - Отсечь пиксели, в которых значения C(x,y) ниже порогового значения T.
- Удалить повторяющиеся углы с помощью применения процедуры поиска локальных максимумов функции отклика (non-maximal suppression). Все полученные ненулевые элементы карты соответствуют углам на изображении.
Детектор Моравеца обладает свойством анизотропии в 8 направлениях смещения окна. Основными недостатками рассматриваемого детектора являются отсутствие инвариантности к преобразованию поворота и возникновение ошибок детектирования при наличии большого количества диагональных ребер [2].
Harris
Как показали исследования, наиболее оптимальным детектором L-связных углов является широко известный детектор Харриса (также его называют оператором Плессея, детектором Харриса и Стефенса, Plessey operator, Harris and Stephens detector, 1988) [5] [6].
Харрис и Стефенс улучшили детектор Моравеца (Moravec), введя анизотропию по всем направлениям, т.е. рассматривают производные яркости изображения для исследования изменений яркости по множеству направлений. Они вводят в рассмотрение производные по некоторым принципиальным направлениям.
Для данного изображения I рассмотрим окно W (обычно размер окна равен 5x5 пикселей, но может зависеть от размера изображения) в центре (x,y), а также его сдвиг на (u,v).
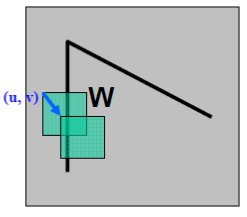
Тогда взвешенная сумма квадрата разностей (sum of squared differences (SSD)) между сдвинутым и исходным окном (т.е. изменение окрестности точки (x,y) при сдвиге на (u,v)) равна:
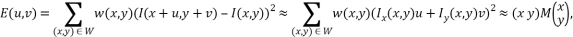
где w(x,y) – весовая функция (обычно используется функция Гаусса или бинарное окно).

M – автокорреляционная матрица:
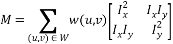
Угол характеризуется большими изменениями функции E(x,y) по всем возможным направлениям (x,y), что эквивалентно большим по модулю собственным значениям матрицы M. Расположение собственных значений приведено на следующем рисунке.
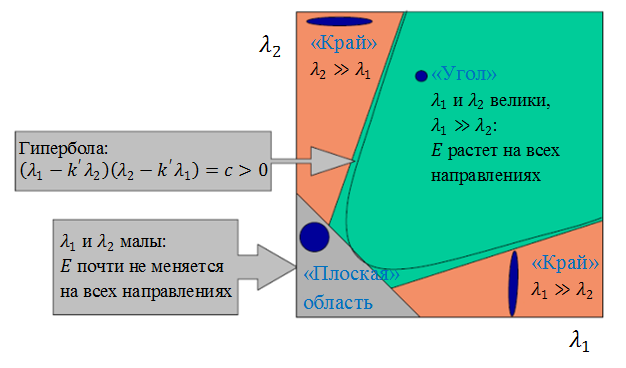
Поскольку напрямую считать собственные значения является трудоёмкой задачей, Харрисом и Стефеном была предложена мера отклика [7]:
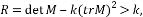
где k – эмпирическая константа, 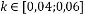 .
.
Таким образом, значение R положительно для угловых особых точек. Затем производится отсечение точек по найденному порогу R (т.е. те точки, у которых значение R меньше некоторого порога, исключаются из рассмотрения). Далее находятся локальные максимумы функции отклика (non-maximal suppression) по окрестности заданного радиуса и выбираются в качестве уголковых особых точек.
Детектор Харриса инвариантен к поворотам, частично инвариантен к аффинным изменениям интенсивности. К недостаткам стоит отнести чувствительность к шуму и зависимость детектора от масштаба изображения (для устранения этого недостатка используют многомасштабный детектор Харриса (multi-scale Harris detector)).
Shi-Tomasi
Угловой детектор Ши-Томаси (Shi-Tomasi или Kanade-Tomasi, 1993) во многом совпадает с детектором Харриса, но различается в вычислении меры отклика: алгоритм напрямую вычисляет значение 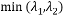 , поскольку делается предположение, что поиск углов будет более стабильным. Авторы используют это же уравнение для анализа оптического потока Лукаса и Канаде (Lucas and Kanade). Подробности алгоритма даны в статьях [8] и [9].
, поскольку делается предположение, что поиск углов будет более стабильным. Авторы используют это же уравнение для анализа оптического потока Лукаса и Канаде (Lucas and Kanade). Подробности алгоритма даны в статьях [8] и [9].
Förstner
Фёрстнер и Гёлч (Förstner and Gülch, 1987) первыми описали метод, который использует ту же самую меру угловатости, что и детектор Харриса. Они использовали более сложную в вычислительном плане реализацию [8]. В отличие от детектора Харриса собственные значения вычисляются явно. Функция отклика угла Фёрстнера определяется следующим образом:
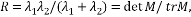
Также для правильности определения считается мера округлости угла, равная: 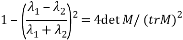 .
.
Детектор Фёрстнера на практике часто используется для расширения возможностей детектора Харриса – нахождению круговых особых точек вместе с углами. Также алгоритм обладает лучшим свойством локализации [2].
Более подробное описание алгоритма представлено в Wikipedia, а также в [10], [11].
SUSAN
Алгоритм SUSAN (Smallest Univalue Segment Assimilation Nucleus) был предложен Смитом и Бреди (Smith и Brady, 1997) [5].
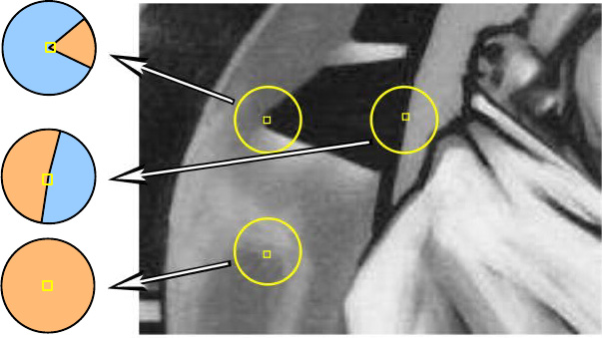
Углы определяются сегментацией круговых окрестностей в схожие (оранжевые) и непохожие (синие) участки. Углы находятся там, где относительная площадь схожих участков (similar USAN) достигает локального минимума ниже определенного порога.
Для каждого пикселя рассматривается круговая область фиксированного радиуса. Центр пикселя называется ядром, значение его интенсивности запоминается. Все остальные пиксели разделяются на 2 категории: в схожие (оранжевые) и непохожие (синие) участки в зависимости от того, схоже ли значение интенсивности ядра, или нет. Там, где присутствует участок изображения под круговой областью без изменений, схожие участки занимают почти всю площадь, на гранях это отношение падает до 50%, на углах еще уменьшается приблизительно до 25%. Таким образом, углы находятся там, где относительная площадь схожих участков (similar USAN) достигает локального минимума ниже определенного порога. Для повышения устойчивости работы алгоритма авторы присваивают ближайшим к ядру пикселям более высокие весовые коэффициенты. Шаги алгоритма следующие:
- Поместить центр круговой маски в ядро.
- Внутри круговой маски вычислить количество пикселей, которые имеют схожую интенсивность с ядром по следующей формуле (найденные пиксели определяют USAN):
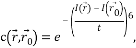
 — точка внутри маски;
— точка внутри маски;
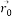 — центр ядра;
— центр ядра;
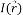 — интенсивность точки
— интенсивность точки  ;
;
t — разностный порог интенсивностей;
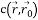 — результат сравнения.
— результат сравнения.
- Вычесть размер USAN из геометрического порога, чтобы получить изображение с углами, по следующей формуле:
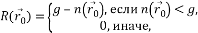
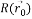 — начальное значение отклика края. Принцип SUSAN: чем меньше область USAN, тем больше отклик края.
— начальное значение отклика края. Принцип SUSAN: чем меньше область USAN, тем больше отклик края.
g — геометрический порог.
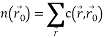 — количество пикселей в USAN, т.е. область USAN.
— количество пикселей в USAN, т.е. область USAN.
- Найти центроиды областей USAN и их близость друг относительно друга и определить ложноположительные.
- Выбрать особые точки с помощью поиска локальных максимумов функции отклика (nonmaximum suppression).
Алгоритм показывает хорошую точность ко всем видам углов, но неустойчив к размытию на изображениях. Подробности даны в [12].
Trajkovic
Тряковиц и Хедли (Miroslav Trajkovic and Mark Hedley, 1998) в статье «Fast corner detection» ввели новый тип детектора — оператор Тряковица [8]. Изначально к нему авторы предъявили требования стать самым популярным детектором углов и обладать минимальной вычислительной стоимостью. Сперва был разработан 4-соседний алгоритм Trajkovic4.
Детектор проверяет область около пикселя путем изучения близлежащих пикселей: пусть c является пикселем, подлежащим рассмотрению, а P является точкой на окружности SN в центре в точке N. Точка P' является точкой противоположной P по диаметру.
Функции отклика (авторы называют её CRN, Corner Request Function) определяется как:
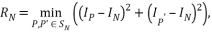
где N – центральная точка;
P и P' – две противоположные по диаметру точки вокруг точки N;
SN – дискретизированная окружность на изображении радиусом 3, 5, 7 пикселей.
Значение CRN будет большим, когда нет направления, в котором центральный пиксель похож на два близлежащих пикселя по диаметру. Поскольку расчет в любом направлении дает верхнюю границу min, то горизонтальное и вертикальное направления проверяются в первую очередь для определения, имеет ли смысл переходить к полному вычислению RN.
В сравнение с детектором Харриса частота повторяемости алгоритма Trajkovic4 хуже, однако локализация сравнима с определением L-связных углов и превосходит на других видах углов.
Также к недостаткам следует отнести то, что этот 4-соседний оператор ложно реагирует на диагональные края и чувствителен к шуму [2]. Поэтому используют 8-связную версию этого алгоритма Trajkovic8. Trajkovic8 отличается от Trajkovic4 тем, как он вычисляет угловатость. Однако Trajkovic8 всё еще находит ложные углы на некоторых диагональных гранях объекта (плохо проявляет себя на искусственных изображениях). Подробные описания алгоритмов приведены в [2] и [8].
FAST
Ростен и Драммонд (Edward Rosten and Tom Drummond, 2005) ввели достаточно успешный алгоритм FAST (Features from Accelerated Segment Test) – особенности ускоренных испытаний сегмента.
В алгоритме рассматривается окружность из 16 пикселей (отрисованная алгоритмом Брезенхема) вокруг точки-кандидата P. Точка является угловой, если для текущей рассматриваемой точки P существуют N смежных пикселей на окружности, интенсивности которых больше IP+t или интенсивности всех меньше IP-t, где IP – интенсивность точки P, t – пороговая величина. Далее необходимо сравнить интенсивность в вертикальных и горизонтальных точках на окружности под номерами 1, 5, 9 и 13 с интенсивностью в точке P (для того, чтобы как можно быстрее отсечь ложные кандидаты). Если для 3 из этих точек выполнится условие IPi>IP+t или IPi<IP+t, i=1,..,4, то проводится полный тест для всех 16 точек [13]. Эксперименты показали, что наименьшее значение N, при котором особые точки начинают стабильно обнаруживаться, равно N=9.

Изначально оригинальным алгоритмом был FAST-12. Существуют модификации алгоритма: древовидные FAST-9 и FAST-12 (the tree based FAST-9 and FAST-12).
Оригинальный алгоритм имеет ряд недостатков, например, вблизи некоторой окрестности может обнаружится несколько особых точек, эффективность алгоритма зависит от порядка обработки изображения и распределения пикселей.
В [14] авторы Edward Rosten, Reid Porter и Tom Drummond (2008) вводят улучшения для алгоритма FAST, заключающиеся в том, что они используют машинное обучение для определения особых точек.
Этот алгоритм они назвали FAST-ER (ER – Enhanced Repeatability, улучшенная повторяемость). Алгоритм стабилен к свойству повторяемости: на одной и той же сцене, рассматриваемой с разных ракурсов, присутствуют особые точки, принадлежащие одним и тем же объектам.
В этом алгоритме используется кольцо окружности более чем 1 пиксель, нежели чем в FAST (48 пикселей). Авторы используют алгоритм ID3 для классификации особых точек (является ли точка-кандидат особой) с помощью деревья решений. Алгоритм ID3 оптимизирует порядок, в котором обрабатываются пиксели, в результате чего получается наиболее вычислительно эффективный детектор.

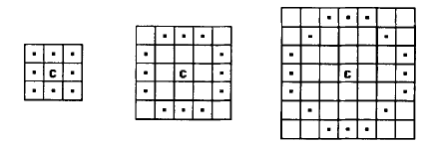
Функция стоимости дерева решений рассчитывается следующим образом:
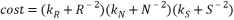
R – мера повторяемости;
N – количество обнаруженных особых точек;
S – количество узлов в дереве решений.
Подробности описаны в [14].
FAST-ER лучше, чем FAST, но медленнее по скорости выполнения. Авторы сделали вывод, что FAST-ER детектор является самым лучшем в отношение к свойству повторяемости.
CSS
Rattarangsi and Chin (1992) [15] предложили алгоритм, основанный на кривизне масштабного пространства (curvature scale space, CSS), обнаруживающий углы на плоских кривых. CSS подходит для извлечения инвариантных геометрических особенностей на плоской кривой в различных масштабах.
Алгоритм определяет особые точки, используя несколько масштабов одного и того же изображения. Однако он является вычислительно сложным и обнаруживает ложные углы на круговых областях. [16]
Farzin Mokhtarian и Riku Suomela (1998) [17] улучшили алгоритм в устойчивости к шуму. Этот алгоритм применяется к черно-белому изображению и включает следующие шаги:
- Применить детектор границ Канни (Canny) к изображению и получить бинарную карту границ.
- Выделить контуры границ из бинарной карты. Проверить концы контуров на смежность с другими, если это так, то дозаполнить границу до соединения. Отметить эту точку как T-связный угол, если конец контура соединяется с границей.
- Вычислить значения кривизны у каждого контура на наибольшем масштабе σhigh. Положить начальными значениями локальные максимумы кривизны, при условии что значение кривизны выше порога t и вдвое выше соседних локальных минимумов.
- Отсортировать углы по убыванию от самого наибольшего масштаба к меньшему с целью улучшения свойства локализации.
- Сравнить T-связные углы с остальными углами и, если они находятся близко друг у другу, удалить один из углов.
На изображении показаны 2 случая промежутков грани: T-связный промежуток отмечается как угол (T-corner point), а промежуток между концами контуров (gap) дозаполняется.
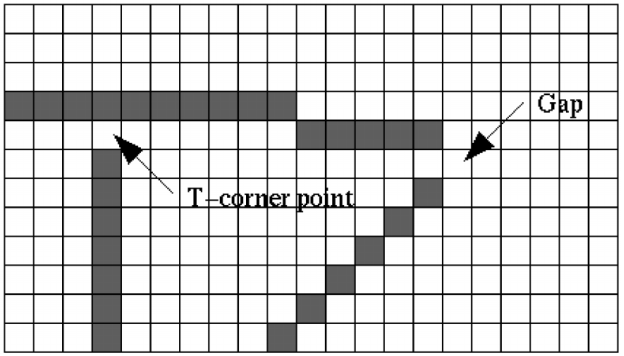
В этом алгоритме есть следующие недостатки: изображение только в одном масштабе используется для определения числа углов (шаг 3), а изображения в нескольких масштабах – для локализации. В результате, алгоритм пропускает углы, когда σ большое, и обнаруживает ложные, когда σ малое. [16]
Были проведены ряд улучшений алгоритма: в 2001 F. Mokhtarian and R. Suomela в статье «Robust image corner detection through curvature scale space» (предложили улучшенный CSS) и в 2008 — He и Yung в статье «Corner detector based on global and local curvature properties», а также детектор CPDA.
Детектор, основанный на глобальных и локальных свойствах кривизны
He и Yung (2008) в статье «Corner detector based on global and local curvature properties» предлагают улучшение алгоритма CSS. Они утверждают, что традиционные алгоритмы вычисления рассматривают локальные свойства изображения, зачастую ложно определяя шум за особые точки либо пропуская мелкие детали объекта. В данном алгоритме балансируют глобальные и локальные свойства уровня кривизны граней для извлечения углов.
В результате He и Yung предлагают следующее решение:
- Обнаружить границы, например, детектором Канни Canny для получения бинарной карты границ.
- Выделить контуры как в алгоритме CSS.
- Вычислить значения кривизны для фиксированного малого масштаба (чтобы не пропустить истинные углы), рассмотреть локальные максимумы абсолютных значений кривизны, которые отметить как потенциальные уголковые кандидаты.
- Вычислить порог, исходя из среднего значения кривизны в рассматриваемой области. Удалить круговые углы путем сравнения значения кривизны угловых кандидатов с адаптивным порогом.
- Вычислить значения углов у оставшихся уголковых кандидатов с использованием адаптивной рассматриваемой области и удалить ложные кандидаты.
- Рассмотреть концы открытых контуров и отметить их как углы, если они не находятся близко друг к другу.
Так, на изображении показывается пример определения кругового угла (round corner) (a) и тупого угла (obtuse corner) (b), который еще не является круговым. Для их определения вычисляются значения кривизны, графики которых показаны на рисунках (c ) и (d).
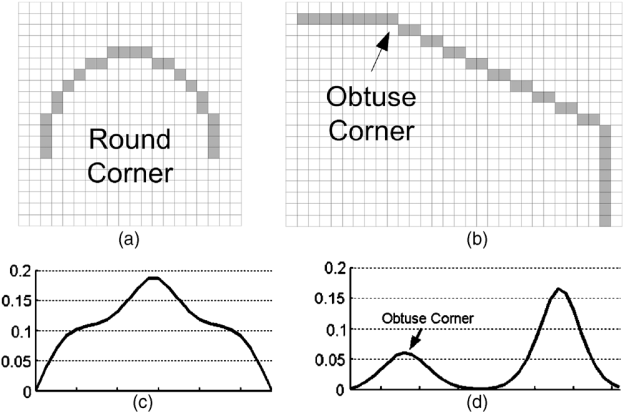
Детали алгоритма объясняются в статье [16].
CPDA
Awrangjeb и Lu ввели новый детектор CPDA (Chord-to-Point Distance Accumulation, 2008) [18].
С одной стороны Гауссиана с большим σ уменьшает шум, но воздействует на локализацию, с другой – Гауссина с малой σ чувствительна к шуму. Для решения этих проблем Awrangjeb и Lu предложили метод chord-to-point distance accumulation (CPDA) с помощью адаптивного порога, основанного на идеи Han и Poston. Метод CPDA использует дискретную оценку кривизны, устойчивую к локальным изменениям. Авторы используют 3 хорды различной длины для оценки 3-х нормированных дискретных значений кривизны в каждой точке сглаженной кривой. [19]
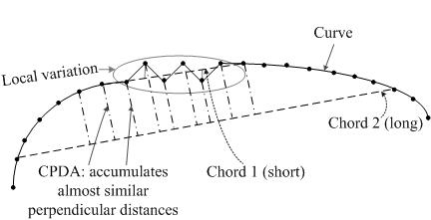
Поскольку детектор использует большую окрестность, он менее чувствителен к шуму и локальным изменениям на кривой. Детектор CPDA является дальнейшим развитием детектора CSS. Шаги:
- Найти границы на изображении, используя детектор границ Канни.
- Выделить контуры границ из бинарной карты.
- Проверить концы контуров на смежность с другими, если это так, то дозаполнить границу до соединения.
- Найти T-соединения и отметить эту точку как T-связный угол.
- Определить состояние каждой границы как петля или линия.
- Размыть изображение, используя небольшое окно Гауссова ядра, чтобы удалить шум и незначительные части изображения.
- Для каждой точки размытой кривой вычислить 3 значения кривизны, используя 3 хорды различной длины.
- Вычислить 3 нормированных значения кривизны для каждой точки кривой и умножить друг на друга.
- Найти локальные максимумы модуля произведения значений кривизны соответствующих особых точек и исключить «слабые» путем сравнения с порогом.
- Для каждого кандидата на особую точку вычислить значения углов и исключить ложные сравнением с порогом.
- Найти углы между концами сглаженных петель (если таковые присутствуют) и обнаруженными углами, если они достаточно удалены от них.
- Каждый из найденных T-связных углов добавить к обнаруженным углам, если он достаточно удален от них. [18]
Выводы
Можно заметить, что современные алгоритмы стали более сложные. Однако детекторы Харриса и FAST являются самыми часто используемыми и вычислительно быстрыми алгоритмами для определения углов.
В статье не рассматриваются такие детекторы, как Harris-Laplace, Hessian-Laplace, DoG, LoG, Harris-Affine, Hessian-Affine, Salient Regions поскольку хоть они и позволяют определять углы, но в большей степени их стоит отнести к детекторам блобов (капель, blob). [5]
Также данная статья не исчерпывает всего множества алгоритмов определения углов, в силу их большого количества и специфики применения к предметным областям. Некоторые из алгоритмов больше представляют теоретический интерес, чем практический. В статье рассмотрены основные алгоритмы определения углов, которые чаще всего встречаются в литературе.
Например, также есть еще следующие алгоритмы (с указанием статей):
- Поворотно-инвариантный оператор DET (вероятно, один из первых детекторов). P.R. Beaudet. Rotationally invariant image operators. In Proc. IAPR1978, pages 579–583, 1978.
- Детектор Kitchen-Rosenfeld. L. Kitchen and A. Rosenfeld. Gray Level Corner Detection. Pattern Recognition Letters, pp. 95-102, 1982.
- Детектор Wang-Brady. H. Wang and M. Brady. Real-time corner detection algorithm for motion estimation. Image and Vision Computing, vol. 13:9, pp. 695-703, 1995.
- Детектор SCD (Structure-based corner detector). Fei Shen, Han Wang. Real Time Gray Level Corner Detector. 2000.
- Детектор COP (Crosses as Oriented Pair). S.C. Bae, I.S. Kweon and C.D. Yoo. COP: a new corner detector. Pattern Recogn. Lett. 2002.
- Улучшенный детектор, основанный на детекторах Harris-Stephen и Shi-Tomasi. Lidia Forlenza, Patrick Carton, Domenico Accardo, Giancarmine Fasano and Antonio Moccia. Real Time Corner Detection for Miniaturized Electro-Optical Sensors Onboard Small Unmanned Aerial Systems. 2012.
- Детектор Zhang. Jun Zhang, Tingjin Luo, Gui Gao, and Lin Lian. Junction Point Detection Algorithm for SAR Image, 2013.
Стоит отметить, что это не весь список.
 [16]
[16]  [2]
[2]
Ниже приведена сравнительная таблица детекторов углов, взятая из [2].
Сравнение детекторов углов (1 – Очень плохо, 2 – плохо, 3 – удовлетворительно, 4 – хорошо, 5 – отлично).
| Оператор (алгоритм) | Эффективность обнаружения | Локализация | Частота повторяемости | Устойчивость к шуму | Скорость |
|---|---|---|---|---|---|
| Beaudet | 3 | 3 | 4 для аффинных преобразований, 2 для масштабирования | 2 | 4 |
| Moravec | 3 | 4 | 3 | 3 | 4 |
| Kitchen & Rosenfeld | 3 | 3 | 3 | 3 | 3 |
| Förstner | 4 | 4 | 5 для аффинных преобразований, 3 для масштабирования | 4 | 2 |
| Plessey | 4 | 4 для L-связных углов, 2 для остальных типов | 5 для аффинных преобразований, если вычисляется анизотропный градиент, 3 для масштабирования | 3 | 2 |
| Deriche | 3 (?) | 4 | 4 | 2 | 4 |
| Wang & Brady | 4 | 4 | 4 | 3 | 4 |
| SUSAN | 4 | 1 для размытых изображений, 4+ иначе | 4 для масштабирования, 2 для аффинных преобразований | 5 | 4 |
| CSS | 4 | 4 | 5 | 4 | Сильно зависит от используемого детектора границ |
| Trajkovic & Hedley (4-neighbours) | 2 | 4 | 3 (не инвариантно к поворотам) | 2 | 5 |
| Trajkovic & Hedley (8-neighbours) | 3 | 4 | 3+ (не инвариантно к поворотам) | 4 | 5 |
| Zheng & Wang | 4 | 4 для L-связных углов, 3 для остальных типов | 5 для аффинных преобразований, 3 для масштабирования | 3 | 3 |
Поведение уголковых детекторов на искусственном изображении Смита (The synthetic test pattern of Smith).
| Оператор (алгоритм) | Результат работы |
|---|---|
| Moravec [2] | 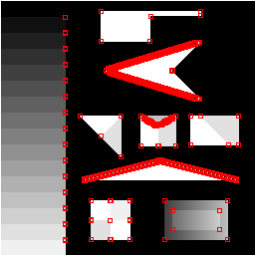 |
| Plessey |  |
| SUSAN | 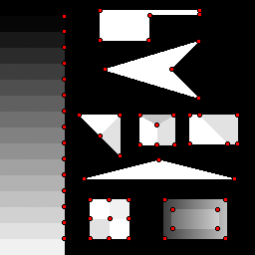 |
| Förstner [10] | 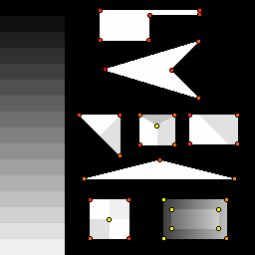 |
| Trajkovic4 |  |
| Trajkovic8 |  |
| Shi-Tomasi [20] | 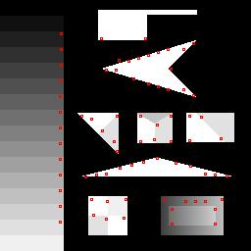 |
Поведение уголковых детекторов на тестовом изображении дома (House Test Image).
| Оператор (алгоритм) | Результат работы |
|---|---|
| Moravec |  |
| Plessey |  |
| SUSAN [16] |  |
| Förstner |  |
| FAST [21] |  |
| Original CSS [16] |  |
| Enhanced CSS [16] |  |
| Corner detector based on global and local curvature properties 2008 [16] |
 |
| Kitchen-Rosenfeld [22] |  |
| COP [22] |  |
P.S.: Я старался провести обзор основных детекторов углов. Надеюсь, что у меня это получилось. Если в статье есть неточности, пожалуйста, отправляйте сообщения в личку. И, может быть, некоторые алгоритмы написаны слишком обобщенно, но если бы я писал все подробности, тогда бы статья разрослась до ещё больших размеров, потеряв бы нить повествования.
Список литературы
[1] Конушин А. Слежение за точечными особенностями сцены (Point feature tracking). Компьютерная графика и мультимедиа. Выпуск №1(5)/2003.
[2] Abhishak Yadav, Poonam Yadav. Digital Image Processing, 2009.
[3] Accurate Junction Detection and Characterization in Natural.
[4] Обзор методов обнаружения характерных точек.
[5] Tinne Tuytelaars, Krystian Mikolajczyk. Local Invariant Feature Detectors: A Survey, 2008.
[6] Harris Corner Detector.
[7] http://www.cs.toronto.edu/~jepson/csc420/notes/imageFeaturesIIBinder.pdf.
[8] M. H. Miroslav Trajkovii. Fast corner detection, 1998.
[9] T. Shi. Good Features to Track, 1994.
[10] V. Rodehorst, A. Koschan. Comparison and evaluation of feature point detectors, 2006.
[11] Lecture 13. Interest Point Detection, 2004.
[12] B. Smith. SUSAN — A new approach to low level, 1997.
[13] E. R. a. T. Drummond. Fusing Points and Lines for High Performance Tracking, 2005.
[14] R. P. a. T. D. Edward Rosten. Faster and better: a machine learning approach to corner detection, 2008.
[15] A. Rattarangsi, W. U. M. W. U. Dept. of Electr. & Comput. Eng. и R. Chin, Scale-based detection of corners of planar curves, Pattern Analysis and Machine Intelligence, IEEE Transactions on (Volume:14, Issue: 4), 1992.
[16] X. Chen He, N. Yung. Corner detector based on global and local curvature, 2008.
[17] R. S. Farzin Mokhtarian. Robust Image Corner Detection Through Curvature Scale Space, 1998.
[18] M. Awrangjeb. CPDA, 2009.
[19] S. M. M. Kahaki, Contour-Based Corner Detection and Classification by Using Mean Projection Transform, 2014.
[20] COMPSCI 773 feature point detection.
[21] Andres Solis Montero, Milos Stojmenović, Amiya Nayak. Robust Detection of Corners and Corner-line links in images. 10th IEEE International Conference on Computer and Information Technology (CIT 2010), 2010.
[22] S.C. Bae, I.S. Kweon and C.D. Yoo. COP: a new corner detector. Pattern Recogn. Lett., 2002.
Автор: lightsource
