Техники сжатия данных
Для сжатия данных придумано множество техник. Большинство из них комбинируют несколько принципов сжатия для создания полноценного алгоритма. Даже хорошие принципы, будучи скомбинированы вместе, дают лучший результат. Большинство техник используют принцип энтропийного кодирования, но часто встречаются и другие – кодирование длин серий (Run-Length Encoding) и преобразование Барроуза-Уилера (Burrows-Wheeler Transform).
Кодирование длин серий (RLE)
Это очень простой алгоритм. Он заменяет серии из двух или более одинаковых символов числом, обозначающим длину серии, за которым идёт сам символ. Полезен для сильно избыточных данных, типа картинок с большим количеством одинаковых пикселей, или в комбинации с алгоритмами типа BWT.
Простой пример:
На входе: AAABBCCCCDEEEEEEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
На выходе: 3A2B4C1D6E38A
Преобразование Барроуза-Уилера (BWT)
Алгоритм, придуманный в 1994 году, обратимо трансформирует блок данных так, чтобы максимизировать повторения одинаковых символов. Сам он не сжимает данные, но подготавливает их для более эффективного сжатия через RLE или другой алгоритм сжатия.
Алгоритм:
— создаём массив строк
— создаём все возможные преобразования входящей строки данных, каждое из которых сохраняем в массиве
— сортируем массив
— возвращаем последний столбец
Алгоритм лучше всего работает с большими данными со множеством повторяющихся символов. Пример работы на подходящем массиве данных (& обозначает конец файла)
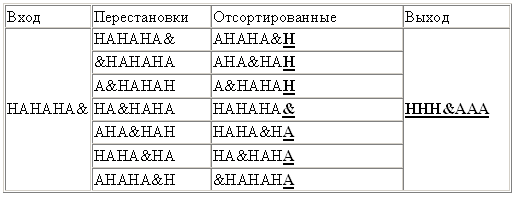
Благодаря чередованию одинаковых символов, вывод алгоритма оптимален для сжатия RLE, которое даёт «3H&3A». Но на реальных данных, к сожалению, настолько оптимальных результатов обычно не получается.
Энтропийное кодирование
Энтропия в данном случае означает минимальное количество бит, в среднем необходимое для представления символа. Простой ЭК комбинирует статистическую модель и сам кодировщик. Входной файл парсится для построения стат.модели, состоящей из вероятностей появления определённых символов. Затем кодировщик, используя модель, определяет, какие битовые или байтовые кодировки назначать каждому символу, чтобы самые часто встречающиеся были представлены самыми короткими кодировками, и наоборот.
Алгоритм Шеннона — Фано
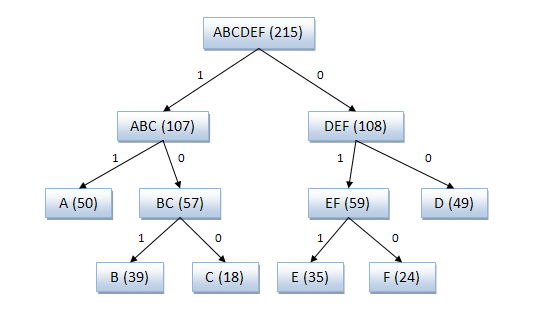
Одна из самых ранних техник (1949 год). Создаёт двоичное дерево для представления вероятностей появления каждого из символов. Затем они сортируются так, чтобы самые часто встречающиеся находились наверху дерева, и наоборот.
Код для символа получается поиском по дереву, и добавлением 0 или 1, в зависимости от того, идём мы налево или направо. К примеру, путь к “А” – две ветки налево и одна направо, его код будет «001». Алгоритм не всегда даёт оптимальные коды из-за методики построения дерева снизу вверх. Поэтому сейчас используется алгоритм Хаффмана, подходящий для любых входных данных.
1. парсим ввод, считаем количество вхождений всех символов
2. определяем вероятность появления каждого из них
3. сортируем символы по вероятности появления
4. делим список пополам так, чтобы сумма вероятностей в левой ветке примерно равнялось сумме в правой
5. добавляем 0 или 1 для левых и правых узлов соответственно
6. повторяем шаги 4 и 5 для правых и левых поддеревьев до тех пор, пока каждый узел не будет «листом»
Кодирование Хаффмана
Это вариант энтропийного кодирования, работающий схожим с предыдущим алгоритмом методом, но двоичное дерево строится сверху вниз, для достижения оптимального результата.
1. Парсим ввод, считаем количество повторений символов
2. Определяем вероятность появления каждого символа
3. Сортируем список по вероятностям (самые частые вначале)
4. Создаём листы для каждого символа, и добавляем их в очередь
5. пока очередь состоит более, чем из одного символа:
— берём из очереди два листа с наименьшими вероятностями
— к коду первой прибавляем 0, к коду второй – 1
— создаём узел с вероятностью, равной сумме вероятностей двух нод
— первую ноду вешаем на левую сторону, вторую – на правую
— добавляем полученный узел в очередь
6. Последняя нода в очереди будет корнем двоичного дерева.
Арифметическое кодирование
Был разработан в 1979 году в IBM для использования в их мейнфреймах. Достигает очень хорошей степени сжатия, обычно большей, чем у Хаффмана, однако он сравнительно сложен по сравнению с предыдущими.
Вместо разбиения вероятностей по дереву, алгоритм преобразует входные данные в одно рациональное число от 0 до 1.
В общем алгоритм таков:
1. считаем количество уникальных символов на входе. Это количество будет представлять основание для счисления b (b=2 – двоичное, и т.п.).
2. подсчитываем общую длину входа
3. назначаем «коды» от 0 до b каждому из уникальных символов в порядке их появления
4. заменяем символы кодами, получая число в системе счисления с основанием b
5. преобразуем полученное число в двоичную систему
Пример. На входе строка «ABCDAABD»
1. 4 уникальных символа, основание = 4, длина данных = 8
2. назначаем коды: A=0, B=1, C=2, D=3
3. получаем число “0.01230013”
4. преобразуем «0.01231123» из четверичной в двоичную систему: 0.01101100000111
Если мы положим, что имеем дело с восьмибитными символами, то на входе у нас 8х8=64 бита, а на выходе – 15, то есть степень сжатия 24%.
Классификация алгоритмов
Алгоритмы, применяющие метод «скользящего окна»
Всё началось с алгоритма LZ77 (1977 год), который представил новую концепцию «скользящего окна», позволившую значительно улучшить сжатие данных. LZ77 использует словарь, содержащий тройки данных – смещение, длина серии и символ расхождения. Смещение – как далеко от начала файла находится фраза. Длина серии – сколько символов, считая от смещения, принадлежат фразе. Символ расхождения показывает, что найдена новая фраза, похожая на ту, что обозначена смещением и длиной, за исключением этого символа. Словарь меняется по мере парсинга файла при помощи скользящего окна. К примеру, размер окна может быть 64Мб, тогда словарь будет содержать данные из последних 64 мегабайт входных данных.
К примеру, для входных данных «abbadabba» результат будет «abb(0,1,'d')(0,3,'a')»
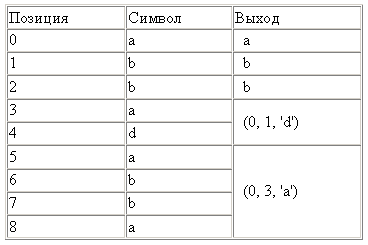
В данном случае результат получился длиннее входа, но обычно он конечно получается короче.
LZR
Модификация алгоритма LZ77, предложенная Майклом Роуде в 1981 году. В отличие от LZ77 работает за линейное время, однако требует большего объёма памяти. Обычно проигрывает LZ78 в сжатии.
DEFLATE
Придуман Филом Кацем в 1993 году, и используется в большинстве современных архиваторов. Является комбинацией LZ77 или LZSS с кодированием Хаффмана.
DEFLATE64
Патентованная вариация DEFLATE с увеличением словаря до 64 Кб. Сжимает лучше и быстрее, но не используется повсеместно, т.к. не является открытым.
LZSS
Алгоритм Лемпеля-Зива-Сторера-Цимански был представлен в 1982 году. Улучшенная версия LZ77, которая просчитывает, не увеличит ли размер результата замена исходных данных кодированными.
До сих пор используется в популярных архиваторах, например RAR. Иногда – для сжатия данных при передаче по сети.
LZH
Был разработан в 1987 году, расшифровывается как «Лемпель-Зив-Хаффман». Вариация LZSS, использует кодирование Хаффмана для сжатия указателей. Сжимает чуть лучше, но ощутимо медленнее.
LZB
Разработан в 1987 году Тимоти Беллом, как вариант LZSS. Как и LZH, LZB уменьшает результирующий размер файлов, эффективно кодируя указатели. Достигается это путём постепенного увеличения размера указателей при увеличении размера скользящего окна. Сжатие получается выше, чем у LZSS и LZH, но скорость значительно меньше.
ROLZ
Расшифровывается как «Лемпель-Зив с уменьшенным смещением», улучшает алгоритм LZ77, уменьшая смещение, чтобы уменьшить количество данных, необходимого для кодирования пары смещение-длина. Впервые был представлен в 1991 году в алгоритме LZRW4 от Росса Вильямса. Другие вариации — BALZ, QUAD, и RZM. Хорошо оптимизированный ROLZ достигает почти таких же степеней сжатия, как и LZMA – но популярности он не снискал.
LZP
«Лемпель-Зив с предсказанием». Вариация ROLZ со смещением = 1. Есть несколько вариантов, одни направлены на скорость сжатия, другие – на степень. В алгоритме LZW4 используется арифметическое кодирование для наилучшего сжатия.
LZRW1
Алгоритм от Рона Вильямса 1991 года, где он впервые ввёл концепцию уменьшения смещения. Достигает высоких степеней сжатия при приличной скорости. Потом Вильямс сделал вариации LZRW1-A, 2, 3, 3-A, и 4
LZJB
Вариант от Джеффа Бонвика (отсюда “JB”) от 1998 года, для использования в файловой системе Solaris Z File System (ZFS). Вариант алгоритма LZRW1, переработанный для высоких скоростей, как этого требует использование в файловой системе и скорость дисковых операций.
LZS
Lempel-Ziv-Stac, разработан в Stac Electronics в 1994 для использования в программах сжатия дисков. Модификация LZ77, различающая символы и пары длина-смещение, в дополнение к удалению следующего встреченного символа. Очень похож на LZSS.
LZX
Был разработан в 1995 году Дж. Форбсом и Т.Потаненом для Амиги. Форбс продал алгоритм компании Microsoft в 1996, и устроился туда работать над ним, в результате чего улучшенная его версия стала использоваться в файлах CAB, CHM, WIM и Xbox Live Avatars.
LZO
Разработан в 1996 Маркусом Оберхьюмером с прицелом на скорость сжатия и распаковки. Позволяет настраивать уровни компрессии, потребляет очень мало памяти. Похож на LZSS.
LZMA
“Lempel-Ziv Markov chain Algorithm”, появился в 1998 году в архиваторе 7-zip, который демонстрировал сжатие лучше практически всех архиваторов. Алгоритм использует цепочку методов сжатия для достижения наилучшего результата. Вначале слегка изменённый LZ77, работающий на уровне битов (в отличие от обычного метода работы с байтами), парсит данные. Его вывод подвергается арифметическому кодированию. Затем могут быть применены другие алгоритмы. В результате получается наилучшая компрессия среди всех архиваторов.
LZMA2
Следующая версия LZMA, от 2009 года, использует многопоточность и чуть эффективнее хранит несжимаемые данные.
Статистический алгоритм Лемпеля-Зива
Концепция, созданная в 2001 году, предлагает проводить статистический анализ данных в комбинации с LZ77 для оптимизирования кодов, хранимых в словаре.
Алгоритмы с использованием словаря
LZ78
Алгоритм 1978 года, авторы – Лемпель и Зив. Вместо использования скользящего окна для создания словаря, словарь составляется при парсинге данных из файла. Объём словаря обычно измеряется в нескольких мегабайтах. Отличия в вариантах этого алгоритма строятся на том, что делать, когда словарь заполнен.
При парсинге файла алгоритм добавляет каждый новый символ или их сочетание в словарь. Для каждого символа на входе создаётся словарная форма (индекс + неизвестный символ) на выходе. Если первый символ строки уже есть в словаре, ищем в словаре подстроки данной строки, и самая длинная используется для построения индекса. Данные, на которые указывает индекс, добавляются к последнему символу неизвестной подстроки. Если текущий символ не найден, индекс устанавливается в 0, показывая, что это вхождение одиночного символа в словарь. Записи формируют связанный список.
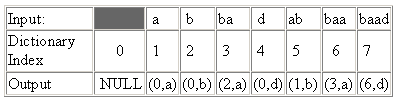
Входные данные «abbadabbaabaad» на выходе дадут "(0,a)(0,b)(2,a)(0,d)(1,b)(3,a)(6,d)"
An input such as «abbadabbaabaad» would generate the output "(0,a)(0,b)(2,a)(0,d)(1,b)(3,a)(6,d)". You can see how this was derived in the following example:
LZW
Лемпель-Зив-Велч, 1984 год. Самый популярный вариант LZ78, несмотря на запатентованность. Алгоритм избавляется от лишних символов на выходе и данные состоят только из указателей. Также он сохраняет все символы словаря перед сжатием и использует другие трюки, позволяющие улучшать сжатие – к примеру, кодирование последнего символа предыдущей фразы в качестве первого символа следующей. Используется в GIF, ранних версиях ZIP и других специальных приложениях. Очень быстр, но проигрывает в сжатии более новым алгоритмам.
LZC
Компрессия Лемпеля-Зива. Модификация LZW, использующаяся в утилитах UNIX. Следит за степенью сжатия, и как только она превышает заданный предел – словарь переделывается заново.
LZT
Лемпель-Зив-Тищер. Когда словарь заполняется, удаляет фразы, использовавшиеся реже всех, и заменяет их новыми. Не получил популярности.
LZMW
Виктор Миллер и Марк Вегман, 1984 год. Действует, как LZMW, но соединяет в словаре не похожие данные, а две последние фразы. В результате словарь растёт быстрее, и приходится чаще избавляться от редко используемых фраз. Также непопулярен.
LZAP
Джеймс Сторер, 1988 год. Модификация LZMW. “AP” означает «все префиксы» — вместо того, чтобы сохранять при каждой итерации одну фразу, в словаре сохраняется каждое изменение. К примеру, если последняя фраза была “last”, а текущая – «next”, тогда в словаре сохраняются „lastn“, „lastne“, „lastnex“, „lastnext“.
LZWL
Вариант LZW от 2006 года, работающий с сочетаниями символов, а не с отдельными символами. Успешно работает с наборами данных, в которых есть часто повторяющиеся сочетания символов, например XML. Обычно используется с препроцессором, разбивающим данные на сочетания.
LZJ
1985 год, Матти Якобсон. Один из немногих вариантов LZ78, отличающихся от LZW. Сохраняет каждую уникальную строку в уже обработанных входных данных, и всем им назначает уникальные коды. При заполнении словаря из него удаляются единичные вхождения.
Алгоритмы, не использующие словарь
PPM
Предсказание по частичному совпадению – использует уже обработанные данные, чтобы предсказать, какой символ будет в последовательности следующим, таким образом уменьшая энтропию выходных данных. Обычно комбинируется с арифметическим кодировщиком или адаптивным кодированием Хаффмана. Вариация PPMd используется в RAR и 7-zip
bzip2
Реализация BWT с открытым исходным кодом. При простоте реализации достигает хорошего компромисса между скоростью и степенью сжатия, в связи с чем популярен в UNIX. Сначала данные обрабатываются при помощи RLE, затем BWT, потом данные особым образом сортируются, чтобы получить длинные последовательности одинаковых символов, после чего к ним снова применяется RLE. И, наконец, кодировщик Хаффмана завершает процесс.
PAQ
Мэтт Махоуни, 2002 год. Улучшение PPM(d). Улучшает их при помощи интересной техники под названием „перемешивание контекста“ (context mixing). В этой технике несколько предсказательных алгоритмов комбинируются, чтобы улучшить предсказание следующего символа. Сейчас это один из самых многообещающих алгоритмов. С его первой реализации было создано уже два десятка вариантов, некоторые из которых ставят рекорды сжатия. Минус – маленькая скорость из-за необходимости использования нескольких моделей. Вариант под названием PAQ80 поддерживает 64 бита и показывает серьёзное улучшение в скорости работы (используется, в частности, в программе PeaZip для Windows).
Автор: SLY_G