Проблема прогнозирования и описания временных рядов будоражит умы учёных и людей уже много лет. Исторически сложилось что модели из эконометрии крайне редко используются в, к примеру, физике или биологии. И наоборот.
1. Полное электронное содержание:
ПЕС (англ. TEC — total electron content) — важная описательная характеристика состояния ионосферы, описывает количество электронов между двумя точками, по прямой. Измеряется в 10¹⁶ электрон/м² = 1 TEC Unit. От ПЕС зависит одна из основных величин в плазме, а именно — плазменная электронная частота. В адиабатическом приближение (без учёта движения ионов) можно получить:
.
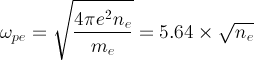В свою очередь для плазмы показатель преломления зависит от плазменной частоты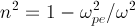 
. Непредсказуемые изменения этого параметра могут сильно потрепать нервы при связи со спутником.
1.1. IONospheric Map Exchange [1]:
Формат данных для распространения карт глобальных карт ПЕС. Был предложен в 1996 году организацией The International GNSS Service. Пример карты можно найти тут. А тут можно найти карты основанные на экспериментальных данных и моделях.
Примеры IONEX карт на 2012 год, 1 января и 23 апреля, полдень по Гринвичу:
2. АвтоРегрессии Скользящего Среднего — АРСС (англ. ARIMA):
Линейная модель предложенная ещё в 20-х — 30-х годах прошлого века [2][3]. Базируется на предположениях что любой ряд зависит от прошлых значений, ошибок и значений ошибок в прошлые моменты времени (все распределены с нулевым средним и неизвестной дисперсией). Ещё одним условием есть стационарность ряда (постоянное значение среднего и независимость от под-выборки выборочной дисперсии и автокорреляции). Для получения стационарного ряда чаще всего используется взятие разностей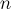 
-го порядка:
,
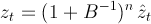где,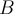 
— оператор сдвига вперёд, соответственно 
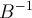— оператор сдвига назад.
Тогда для стационарного ряда можно записать:
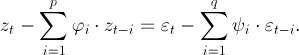
Итого модель зависит от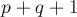 
неизвестного параметра.
Система уравнений для начальных оценок АР:
(*)
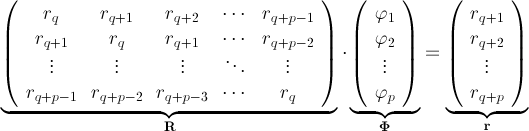И для СС части модели:
(**)
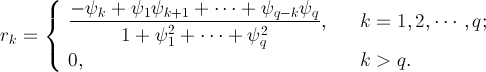Где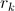 
коэффициент линейной корреляции:
,
, 
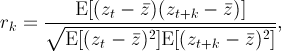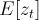— математическое ожидание.
Решая систему уравнений (*), к примеру, методом Гаусса и систему уравнение (**) методом Ньютона будут получены начальные оценки для параметров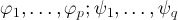 
. Дальнейшее уточнение проводится методами оптимизации, например, Левенберга-Марквардта 4.
3. Software:
Приведу небольшой список приложений которые позволяют моделировать ряды таким методом:
4. Результаты:
Порядки модели были выбраны из предположения что максимальное правдоподобие будет, хм!, максимальным. Для всех следующих моделей это p = 2, q = 0.
Далее изображения ПЕС поданы в одинаковой шкале, а для квадрата разницы указано максимальное значение:
Реальный ПЕС на 7-ое марта 2011:
Прогноз на основание данных без изменений:
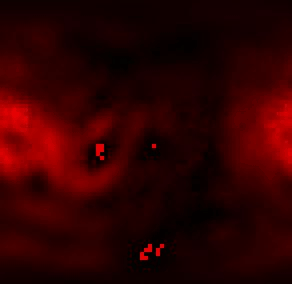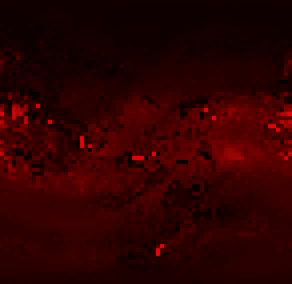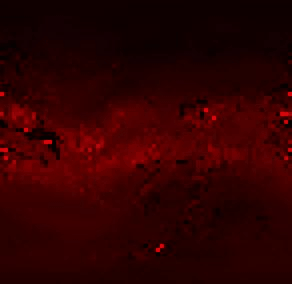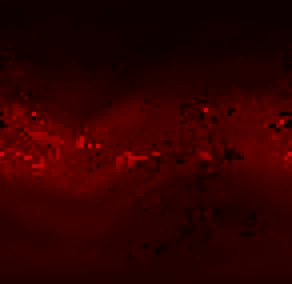
Ярко красные точки на прогнозе это отрицательные величины. В этих точках или неправильная модель, или неправильные расчёты.
Квадрат разницы (максимальное значение — 6400):
Прогноз на основание только точек которые отстают по времени на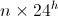 
:
Квадрат разницы (максимальное значение — 594):
5. Выводы:
Прогнозирование делать можно. При нескольких условиях. Первое это спокойное Солнце. Так что магнитные бури мы предсказать этим методом не сумеем. И второе это понимание того, что такая модель отбрасывает практически всю физики процессов, которые происходят в ионосфере Земли.
[1]: Schaer S., Gurther W. 'IONEX: The IONosphere Map Exchange' Darmstadt (1998)
[2]: Yule G. Phil. Trans. Roy. soc. London A, V. 226, pp. 267-298 (1927)
[3]: Walker G. Proc. Roy. soc. London A, V. 131, pp. 518-532, (1931)
[4]: Википедия: Алгоритм Левенберга — Марквардта
Автор: m0nhawk
