Одним замечательным летним вечером, я в пылу спора имел глупость заметить, что можно написать быстро работающее решето Эратосфена на CUDA. N = 1000000000 (девять нулей) как цель. And the legend has begun…
Не буду опускаться в подробности алгоритма, о нем можно почитать, например, тут и сразу покажу код, которым я располагал на тот момент:
#include <iostream>
#include <math.h>
using namespace std;
int main()
{
double number = 1000000000;
bool* a = new bool[int(number/2)];
int i,j,result;
for (i=0; i<number/2; i++)
a[i] = true;
for (i=3; i<=floor(sqrt(number)); i+=2)
if (a[i/2])
for (j=i*i; j<=number; j+=i*2)
a[j/2]=false;
result = 0;
for (i=0; i<number/2; i++)
if (a[i]) result++;
cout << result << endl;
delete[] a;
return 0;
}
Однопоточный немного оптимизированный код, который работает на 14-15 секунд на Core i3 330M и затрачивает большое количество памяти. С него и начнем.
Блочное решето
Залогом успешного распараллеливания является разделение задачи на независимые части, дабы исключить проблемы с памятью, возникающие при параллельном обращении к ней. И тут весьма кстати приходится так называемое блочное решето, которое позволяет сэкономить память и разделить большое решето на некоторое число маленьких. Возможно это становится благодаря одному интересному свойству решета, а именно: все составные числа от корня из N и до N будут кратны простым из промежутка от 2 до корня из N. Иначе говоря, найдя простые до корня из N (назовем это предварительным решетом) останется только для каждого блока найти элементы с которых начинать вычеркивать.
Первое, что приходит на ум, это перебор делителей и в случае делимости начинать вычеркивать с шагом в делитель. Но даже по примерным прикидкам подобный подход окажется очень неэффективным, даже с учетом все возможных оптимизаций.
Если взять N = 10000, то только для нахождения простых (1229 штук) понадобится чуть меньше тридцати тысяч проверок, кроме того, не стоит забывать, что каждый элемент проверяется как минимум один раз, то есть это еще десять тысяч проверок.
К слову, данный вариант был реализован на CUDA и повесил видеокарту GeForce 9600 GT почти на час.
Попытка номер два
На этом все могло и закончиться. Но решение пришло, как всегда неожиданно. И выглядело оно следующим образом.
Предположим, что N = 100, число блоков равно десяти, как и размер части. В предварительном решете будут четыре элемента: 2, 3, 5, 7. Так как размер предварительного решета равен размеру части, то начинать можно со второго блока. Начинается он с известного нам числа 11. Примером простого числа по которому будет происходить вычеркивание нам послужит тройка. Двойку не учитываю по причине очевидной оптимизации с ее участием, но об этом позже. Предыдущий блок окончился на 10, последний вычеркнутый элемент кратный тройке — девять, находится в одном элементе от конца блока. Следовательно, если из тройки вычесть этот «хвост», то можно найти сколько в следующем блоке осталось до элемента, который надо быдет вычеркнуть — до 12.
И так для каждого простого из предварительного решета. Кроме того, оптимизации используемые в «обычном» решете применимы и здесь, а именно: экономия памяти путем исключения четных элементов и вычеркивание, начиная с числа в квадрате.
От теории, к практике
Осталось все теоритические наработки собрать вместе. Вот что из этого вышло:
for(i=0; i<PARTS; i++)
{
for(j=0; j<PART_SIZE/2; j++)
part[j] = true;
for(j=1; j<result1; j++)
{
offset = 0;
if(part1[j]*part1[j]<=(i+1)*PART_SIZE)
{
offset = i*PART_SIZE+part1[j]-i*PART_SIZE%part1[j];
if(offset%2 == 0) offset += part1[j];
}
else break;
for(k=offset; k<=(i+1)*PART_SIZE; k+=part1[j]*2)
if(part[(k-(i*PART_SIZE)-1)/2]) part[(k-(i*PART_SIZE)-1)/2] = false;
}
if(i==0) result = j - 1;
for(j=0; j<PART_SIZE/2; j++)
if(part[j]) result++;
}
Добавлять сюда код предварительного решета не считаю необходимым, ибо он идентичен «обычному» решету.
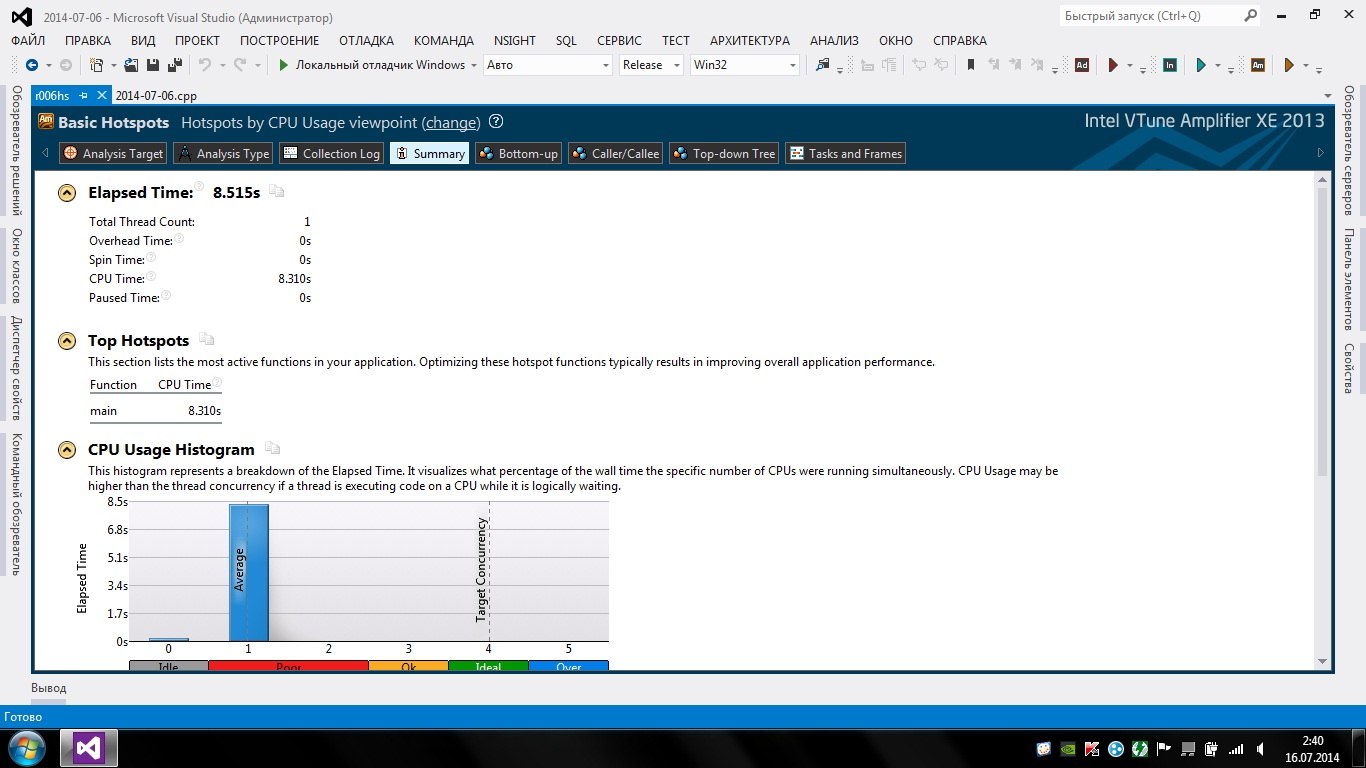
Разделение решета
На достигнутом было решено не останавливаться, поэтому быстро была написана версия работающая в два потока.
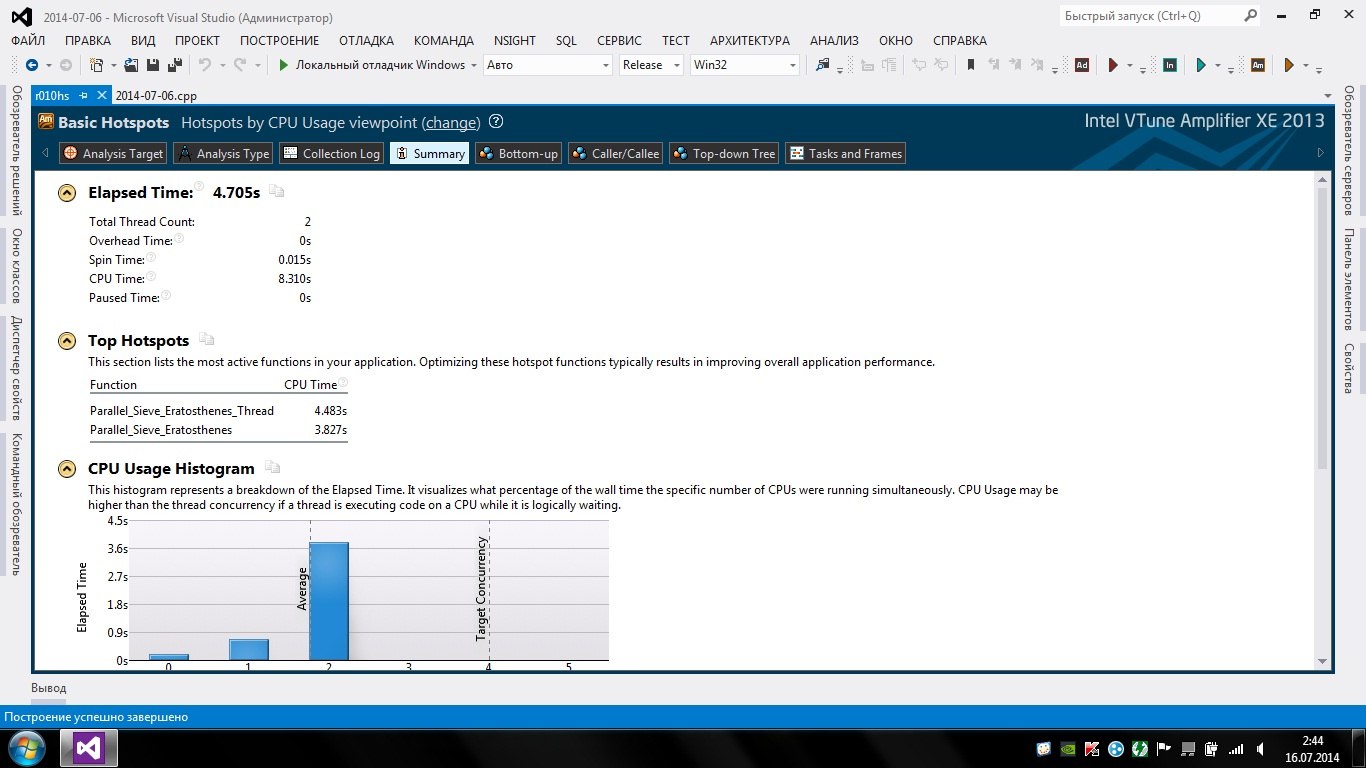
Но был один фактор, который замедлял выполение, второй поток, работающий со второй половиной решета, оказывался медленее основного. Сместив «разрез» решета, удалось ускорить выполнение почти на полсекунды.
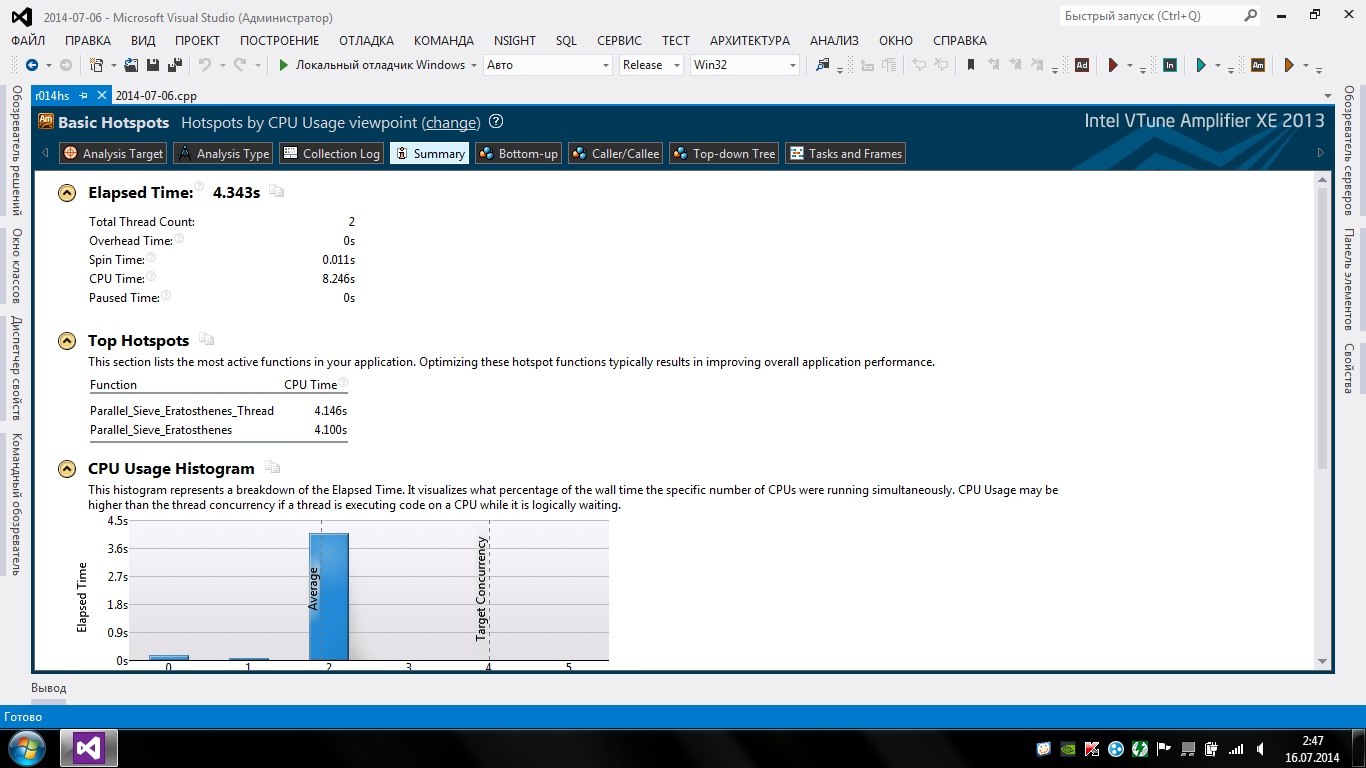
Решето переезжает
Проверенный на CPU алгоритм, был перенесен на GPU. Опытным путем были установлены размеры грида и части решета, которые позволяли достичь наибольшую производительность.
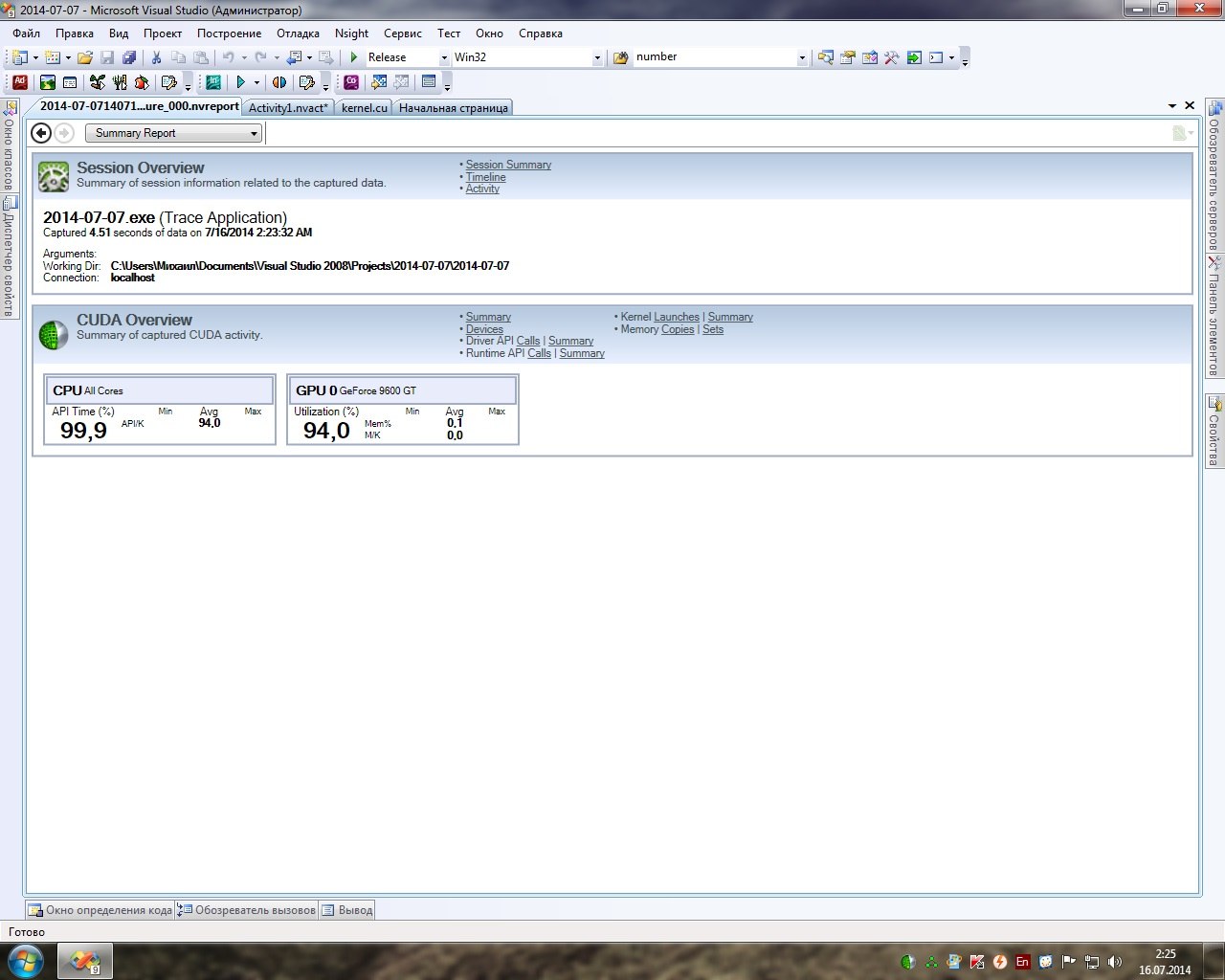
На этом все, всем спасибо за внимание!
Автор: zobov_mihail






