Disclaimer: пост написан по мотивам данного. Я подозреваю, что большинство читателей прекрасно знает, как работает Наивный Байесовский классификатор, поэтому предлагаю лишь мельком хотя бы глянуть на то, о чём там говорится, перед тем как переходить под кат.
Решение задач с помощью алгоритмов машинного обучения давно и прочно вошло в нашу жизнь. Это произошло по всем понятным и объективным причинам: дешевле, проще, быстрее, чем явно кодить алгоритм решения каждой отдельной задачи. До нас, обычно, доходят «черные ящики» классификаторов (вряд ли тот же ВК предложит вам свой корпус размеченных имен), что не позволяет ими управлять в полной мере.
Здесь я бы хотел рассказать о том, как попробовать добиться «лучших» результатов работы бинарного классификатора, о том какие характеристики бинарный классификатор имеет, как их измерять, и как определить, что результат работы стал «лучше».
Теория. Краткий курс
1. Бинарная классификация
Пусть 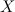 — множество объектов,
— множество объектов, 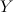 — конечное множество классов. Классифицировать объект — использовать отображение
— конечное множество классов. Классифицировать объект — использовать отображение 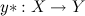 . Когда
. Когда 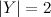 , такая классификация называется бинарной, потому что у нас всего 2 варианта на выходе. Для простоты дальше будем считать, что
, такая классификация называется бинарной, потому что у нас всего 2 варианта на выходе. Для простоты дальше будем считать, что 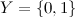 , поскольку абсолютно любую задачу бинарной классификации можно к этому привести. Обычно, результатом отображения объекта в класс является действительное число, и, если оно выше заданного порога, то объект классифицируется, как позитивный, и его класс — 1.
, поскольку абсолютно любую задачу бинарной классификации можно к этому привести. Обычно, результатом отображения объекта в класс является действительное число, и, если оно выше заданного порога, то объект классифицируется, как позитивный, и его класс — 1.
2. Таблица сопряженности бинарного классификатора
Очевидно, что предсказанный класс объекта, полученный в результате отображения 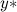 , может либо совпасть в реальным классом, либо нет. Итого 4 варианта в сумме. Это очень наглядно демонстрируется данной табличкой:
, может либо совпасть в реальным классом, либо нет. Итого 4 варианта в сумме. Это очень наглядно демонстрируется данной табличкой:
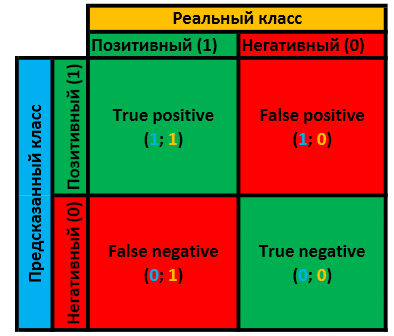
Если мы знаем количественные значения каждой из оценок — мы знаем всё что можно о данном классификаторе и можем копать дальше.
(Я намеренно не использую термины типа «ошибка 1го рода», потому что мне это кажется неочевидным и ненужным)
Дальше будем использовать следующие обозначения:
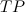 — количество True Positive результатов на данной выборке.
— количество True Positive результатов на данной выборке.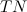 — количество True Negative результатов на данной выборке.
— количество True Negative результатов на данной выборке.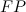 — количество False Positive результатов на данной выборке.
— количество False Positive результатов на данной выборке.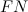 — количество False Negative результатов на данной выборке.
— количество False Negative результатов на данной выборке.
3. Характеристики бинарного классификатора
Точность (precision) — показывает, сколько из предсказанных позитивных объектов, оказались действительно позитивными.
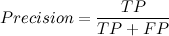
Полнота (recall) — показывает, сколько от общего числа реальных позитивных объектов, было предсказано, как позитивный класс.
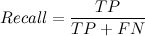
Эти две характеристики являются основными для любого бинарного классификатора. Какая из характеристик важнее — всё зависит от задачи. Например, если мы хотим создать «школьную поисковую систему», то в наших интересах будет убрать «недетский» контент из выдачи, и тут гораздо важнее полнота, чем точность. В случае же определения пола имени — нам скорее интересна точность, чем полнота.
F-мера (F-measure) — характеристика, которая позволяет дать оценку одновременно по точности и полноте.
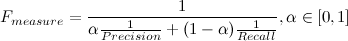
Коэффициент 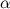 задаёт соотношение весов точности и полноты. Когда
задаёт соотношение весов точности и полноты. Когда 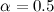 , F-мера придаёт одинаковый вес обеим характеристикам. Такая F-мера называется сбалансированной, или
, F-мера придаёт одинаковый вес обеим характеристикам. Такая F-мера называется сбалансированной, или 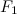
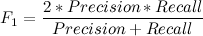
False Positive Rate (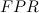 ) — показывает, сколько от общего числа реальных негативных объектов, оказались предсказанными неверно.
) — показывает, сколько от общего числа реальных негативных объектов, оказались предсказанными неверно.
4. ROC-кривая и её AUC
ROC-кривая — график, который позволяет оценить качество бинарной классификации. График показывает зависимость TPR(полноты) от FPR при варьировании порога. В точке (0,0) порог минимален, точно так же минимальны и TPR и FPR. Идеальным случаем для классификатора является проход графика через точку (0,1). Очевидно, что график данной функции всегда монотонно не убывает.
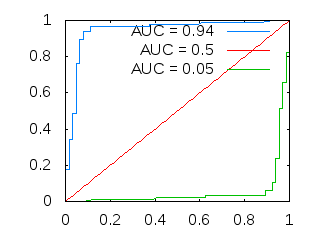
AUC (Area Under Curve) — в области бинарной классификации, данный термин (площадь под графиком) используется исключительно в отношении ROC-кривой. AUC даёт количественную характеристику ROC-кривой: чем больше — тем лучше. AUC — эквивалентна вероятности, что классификатор присвоит большее значение случайно выбранному позитивному объекту, чем случайно выбранному негативному объекту. Именно поэтому ранее было сказано, что, обычно, позитивному классу ставится оценка выше, чем негативному.
Когда AUC = 0.5, то данный классификатор равен случайному. Если AUC < 0.5, то можно просто перевернуть выдаваемые значения классификатором.
Кросс валидация
Методов кросс валидации (оценки качества бинарного классификатора) существует много, и это — тема для отдельной статьи. Здесь я хочу просто рассмотреть один из самых популярных методов, чтобы понять, как эта штука вообще работает, и зачем она нужна.
Построить ROC-кривую, конечно же, можно по любой выборке. Однако, ROC-кривая, построенная по обучающей выборке, будет смещена влево-вверх из-за переобучения. Чтобы этого избежать и получить наиболее объективную оценку, используется кросс валидация.
K-fold cross validation — пул разбивается на k фолдов, затем каждый фолд используется для теста, в то время как остальные k-1 фолдов — для обучения. Значение параметра k может быть произвольным. В данном случае я использовал его равным 10. Для предоставленного классификатора пола имени получились следующие результаты AUC (get_features_simple — одна значимая буква, get_features_complex — 3 значимых буквы)
| fold | get_features_simple | get_features_complex |
| 0 | 0.978011 | 0.962733 |
| 1 | 0.96791 | 0.944097 |
| 2 | 0.963462 | 0.966129 |
| 3 | 0.966339 | 0.948452 |
| 4 | 0.946586 | 0.945479 |
| 5 | 0.949849 | 0.989648 |
| 6 | 0.959984 | 0.943266 |
| 7 | 0.979036 | 0.958863 |
| 8 | 0.986469 | 0.951975 |
| 9 | 0.962057 | 0.980921 |
| avg | 0.9659703 | 0.9591563 |
Практика
1. Подготовка
Весь репозиторий здесь.
Я взял тот же размеченный файл и заменил в нём «m» на 1, «f» — 0. Данный пул будем использовать для обучения, как и автор предыдущей статьи. Вооружившись первой страницей выдачи любимого поисковика и awk, я наклепал список имён, которых нет в изначальном. Данный пул будет использоваться для теста.
Изменил функцию классификации так, чтобы она возвращала вероятности позитивного и негативного классов, а не логарифмические показатели.
def classify2(classifier, feats):
classes, prob = classifier
class_res = dict()
for i, item in enumerate(classes.keys()):
value = -log(classes[item]) + sum(-log(prob.get((item, feat), 10**(-7))) for feat in feats)
if (item is not None):
class_res[item] = value
eps = 709.0
posVal = '1'
negVal = '0'
posProb = negProb = 0
if (abs(class_res[posVal] - class_res[negVal]) < eps):
posProb = 1.0 / (1.0 + exp(class_res[posVal] - class_res[negVal]))
negProb = 1.0 / (1.0 + exp(class_res[negVal] - class_res[posVal]))
else:
if class_res[posVal] > class_res[negVal]:
posProb = 0.0
negProb = 1.0
else:
posProb = 1.0
negProb = 0.0
return str(posProb) + 't' + str(negProb)
2. Реализация и использование
Как написано в заголовке, моей задачей было заставить работать бинарный классификатор лучше, чем он работает по умолчанию. В данном случае, мы хотим научиться определять пол имени, лучше чем по вероятности Наивного Байеса 0.5. Для этого и была написана эта простейшая утилита. Написана она на С++, потому что gcc есть везде. Сама реализация ничего интересного, как мне кажется, не представляет. С ключом -? или --help можно почитать справку, я постарался описать её максимально подробно.
Ну а теперь, собственно то, к чему мы шли: оценка классификатора и его тюнинг. На выходе nbc.py создаёт простыню из файлов с результатами классификации, прямо их я и использую далее. Для наших целей, нам будет наглядно увидеть графики точности от порога, полноты от порога и F-меры от порога. Их можно построить следующим образом:
$ ./OptimalThresholdFinder -A 3 -P 1 < names_test_pool.txt_simple -x thr -y prc -p plot_test_thr_prc_simple.txt
$ ./OptimalThresholdFinder -A 3 -P 1 < names_test_pool.txt_simple -x thr -y tpr -p plot_test_thr_tpr_simple.txt
$ ./OptimalThresholdFinder -A 3 -P 1 < names_test_pool.txt_simple -x thr -y fms -p plot_test_thr_fms_simple.txt
$ ./OptimalThresholdFinder -A 3 -P 1 < names_test_pool.txt_simple -x thr -y fms -p plot_test_thr_fms_0.7_simple.txt -a 0.7Для образовательных целей, я сделал 2 графика F-меры от порога, с разными весами. Второй вес был выбран 0.7, потому что в нашей задаче нам больше интересна точность, чем полнота. График по умолчанию строится на основе 10000 различных точек, это очень много для таких простых данных, но это неинтересные тонкости оптимизации. Точно так же построив данные графиков для get_features_complex, получаем следующие результаты:
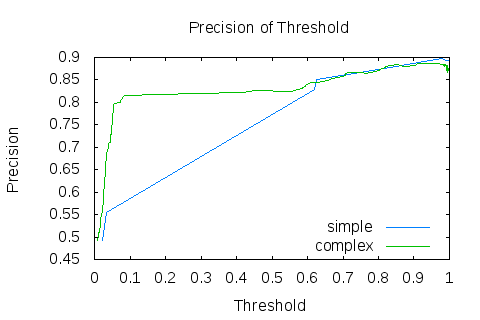
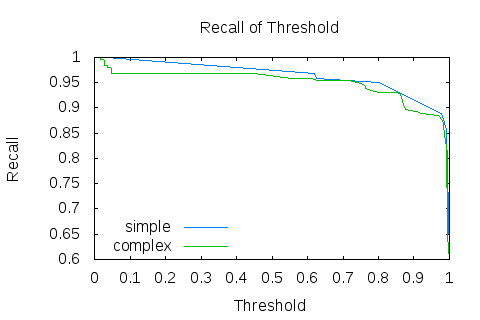
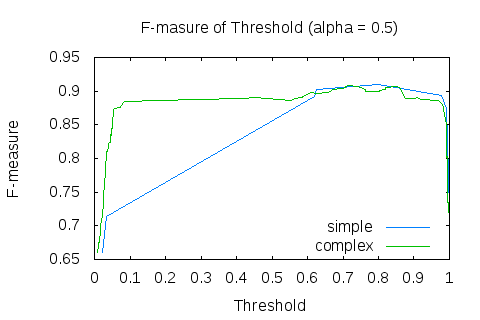
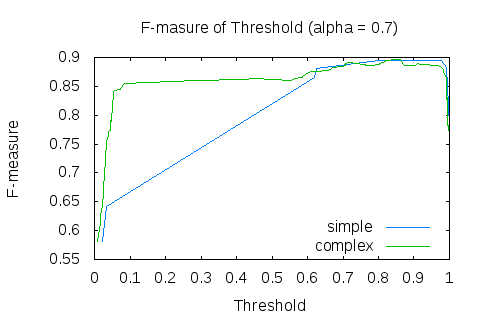
Из графиков становится очевидно, что классификатор показывает лучшие результаты отнюдь не при пороге 0.5. График F-меры явственно демонстрирует, что «сложная фича» даёт лучший результат на всём варьировании порога. Это довольно логично, учитывая, что на то она и «сложная». Получим значения порога, при которых F-мера достигает максимума:
$ ./OptimalThresholdFinder -A 3 -P 1 < names_test_pool.txt_simple --target fms --argument thr --argval 0
Optimal threshold = 0.8 Target function = 0.911937 Argument = 0.8
$ ./OptimalThresholdFinder -A 3 -P 1 < names_test_pool.txt_complex --target fms --argument thr --argval 0
Optimal threshold = 0.716068 Target function = 0.908738 Argument = 0.716068Согласитесь, эти значения гораздо лучше тех, что оказались при пороге по умолчанию 0.5.
Заключение
Такими простыми манипуляциями, мы смогли подобрать оптимальный порог Наивного Байеса для определения пола имени, который работает лучше порога по умолчанию. Тут встаёт резонный вопрос, как мы определили, что он работает «лучше»? Я не раз упомянул о том, что в данной задаче нам важнее точность, чем полнота, однако вопрос о том насколько она важнее — очень и очень сложный, поэтому для оценки работы классификатора использовалась сбалансированная F-мера, которая в данном случае может являться объективным показателем качества.
Что гораздо интереснее, результаты работы бинарного классификатора на основе «простой» и «сложной» фичи в итоге оказались примерно одинаковыми, отличаясь значением оптимального порога.
Автор: zo_oz




![Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс] Как обхитрить мозг и заставить его полюбить сложные задачи [Дофаминовый детокс]](https://www.pvsm.ru/wp-content/plugins/contextual-related-posts/timthumb/timthumb.php?src=http%3A%2F%2Fwww.pvsm.ru%2Fimages%2F2024%2F05%2F10%2Fkak-obhitrit-mozg-i-zastavit-ego-polyubit-slojnye-zadachi-dofaminovyi-detoks-9.jpg&w=100&h=100&zc=1&q=75)

